Линейные углы двугранного угла равны прямые параллельны (3 видео)

Линейные углы двугранного угла равны прямые параллельны

Замечание . Иногда говорят, что двугранный угол α a β образован двумя полуплоскостями α и β , имеющими общую граничную прямую a .

Фигуры, образованные двумя страницами одной книги, двумя соседними гранями куба, — модели двугранного угла.

Для измерения двугранного угла введём понятие его линейного угла. На ребре a двугранного угла α a β отметим произвольную точку O и в гранях α и β проведём из точки O соответственно лучи OA и OB , перпендикулярные ребру a (рис. 96, а ). Угол AOB , образованный этими лучами, называется линейным углом двугранного угла α a β .

Так как OA ⊥ a и OB ⊥ a , то плоскость AOB перпендикулярна прямой a . Это означает, что линейный угол двугранного угла есть пересечение данного двугранного угла и плоскости, перпендикулярной его ребру .

Вследствие произвольного выбора точки O на ребре двугранного угла заключаем, что двугранный угол имеет бесконечное множество линейных углов. Докажем, что все они равны. Действительно, рассмотрим два линейных угла AOB и A 1 O 1 B 1 двугранного угла α a β (рис. 96, б ). Лучи OA и O 1 A 1 лежат в одной грани α и перпендикулярны прямой a — ребру двугранного угла, поэтому они сонаправлены. Аналогично получаем, что сонаправлены лучи OB и O 1 B 1 . Тогда ∠ AOB = ∠ A 1 O 1 B 1 (как углы с сонаправленными сторонами).

Таким образом, нами доказана теорема.

Теорема 27. Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла.

Иначе говоря, все линейные углы данного двугранного угла равны между собой.

Это позволяет ввести следующее определение.

Определение. Величиной двугранного угла называется величина его линейного угла.

Величина двугранного угла, измеренная в градусах, принадлежит промежутку (0 ° ; 180 ° ).

На рисунке 97 изображён двугранный угол, градусная мера (величина) которого равна 30 ° . В этом случае также говорят, что двугранный угол равен тридцати градусам.

Двугранный угол является острым (рис. 98, а ), прямым (рис. 98, б ) или тупым (рис. 98, в ), если его линейный угол соответственно острый, прямой или тупой.

Заметим, что аналогично тому, как и на плоскости, в пространстве определяются смежные (рис. 99, а ) и вертикальные (рис. 99, б ) двугранные углы . При этом справедливы и аналогичные теоремы о величинах этих углов.

Попробуйте доказать самостоятельно следующие два утверждения, важные для решения задач.

 На гранях двугранного угла величины α взяты точки A и B ; A 1 и B 1 — проекции этих точек на ребро двугранного угла; AA 1 = a ; BB 1 = b ; A 1 B 1 = h . Тогда

AB = .

 Если внутри двугранного угла величины α взята точка на расстояниях a и b от граней двугранного угла, то её расстояние от ребра двугранного угла равно .

14.2. Угол между двумя плоскостями

Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром (рис. 100). Если величина одного из них равна ϕ , то величины трёх остальных равны соответственно 180 ° – ϕ , ϕ , 180 ° – ϕ (почему?). Наименьшая из этих величин принимается за величину угла между данными пересекающимися плоскостями.

Определение. Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных при их пересечении.

Угол между параллельными или совпадающими плоскостями полагается считать равным нулю.

Если величина угла между плоскостями α и β равна ϕ , то пишут: ( α ; β ) = ϕ .

Так как двугранный угол измеряется своим линейным углом, то из выше приведённого определения следует, что угол между пересекающимися плоскостями равен углу между пересекающимися прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения (см. рис. 100). Это означает, что величина угла между плоскостями принадлежит промежутку [0 ° ; 90 ° ] .

ЗАДаЧа. Отрезок DM длиной 3,2 перпендикулярен плоскости ромба ABCD ( ∠ ADC — тупой). Диагонали ромба равны 12 и 16. Найти углы между плоскостями:

а) ABC и MBC ; б) AMD и CMD .

Решение. а) Пусть DE — высота ромба ABCD (рис. 101). Тогда по теореме о трёх перпендикулярах ME ⊥ BC и ∠ DEM = ϕ — линейный угол двугранного угла, образованного плоскостями ABC и MBC . Найдём величину этого угла.

По условию задачи DM ⊥ ( ABC ), поэтому ⧌ MDE — прямоугольный, значит, tg ϕ = . Так как DE — высота ромба ABCD , то DE = , где S — площадь этого ромба. Сторона BC ромба является гипотенузой прямоугольного треугольника BOC , катеты OB и OC которого равны 6 и 8. Значит, BC = = = 10.

Учитывая, что S = • AC • BD = •12•16 = 96, находим: DE = = 9,6. Тогда tg ϕ = = = , откуда ϕ = arctg .

б) Так как отрезок DM — перпендикуляр к плоскости ромба ABCD , то AD ⊥ DM , CD ⊥ DM , значит, ∠ ADC = ψ — линейный угол двугранного угла, образованного пересекающимися плоскостями ADM и CDM . Найдём этот угол.

В треугольнике ACD по теореме косинусов находим

cos ψ = = = – ,

откуда ψ = arccos .

Ответ: а) arctg ; б) arccos .

Содержание

Двугранные углы. Углы между плоскостями. Перпендикулярность плоскостей
Двугранные углы
Равенство и неравенство двугранных углов
🔥 Видео

Видео:ДВУГРАННЫЙ УГОЛ 10 11 класс прямой двугранный уголСкачать

Двугранные углы. Углы между плоскостями.
Перпендикулярность плоскостей

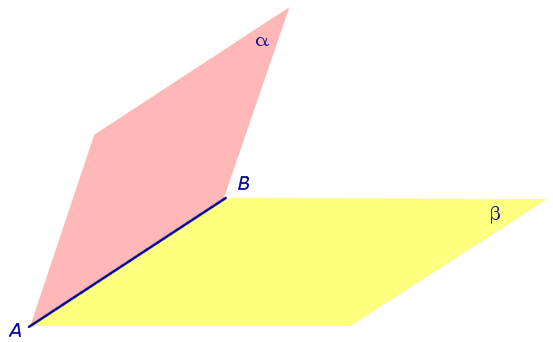
Двугранным углом называют часть пространства, ограниченную двумя полуплоскостями с общей границей (рис. 1)

Полуплоскости α и β , ограничивающие двугранный угол, называют гранями двугранного угла , а их общую границу AB называют ребром двугранного угла .

Двугранные углы называют равными двугранными углами , если их можно совместить.

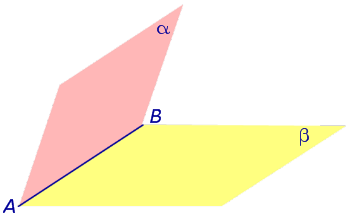
При пересечении двух плоскостей образуются четыре двугранных угла (рис. 2). Наименьший из этих углов обычно и называют углом между плоскостями .

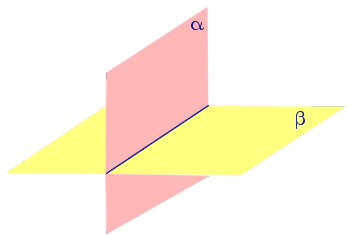
Если при пересечении двух плоскостей образовалось 4 равных двугранных угла, то такие двугранные углы называют прямыми двугранными углами , а сами плоскости называют перпендикулярными плоскостями (рис. 3).

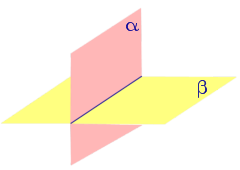
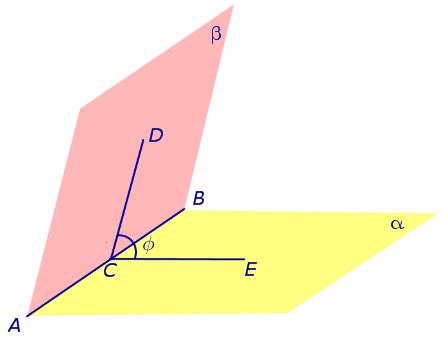
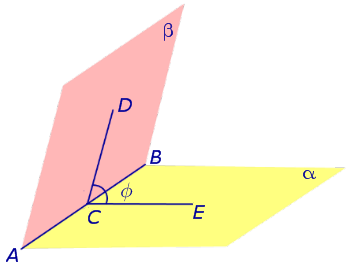
Выберем произвольную точку С на ребре AB двугранного угла и проведем через нее перпендикуляры CD и CE в каждой из граней двугранного угла. Угол DCE , образованный перепендикулярами CD и CE, называют линейным углом двугранного угла (рис. 4).

На рисунке 4 угол φ является линейным углом двугранного угла с гранями α и β и ребром AB .

Линейные углы двугранных углов используются, в частности, для того, чтобы измерять двугранные углы. Например, если линейный угол двугранного угла равен 30° ( или 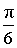) , то и двугранный угол равен 30° ( радиан ) . Соответственно, прямой двугранный угол равен 90° ( радиан ) .

Видео:10 класс, 22 урок, Двугранный уголСкачать

Двугранные углы

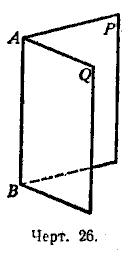
Определения. Часть плоскости, лежащая по одну сторону от какой-либо прямой, лежащей в этой плоскости, называется полуплоскостью. Фигура, образованная двумя полуплоскостями (P и Q, черт. 26), исходящими из одной прямой (AB), называется двугранным углом. Прямая AB называется ребром, а полуплоскости Р и Q — сторонами или гранями двугранного угла.

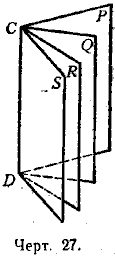
Такой угол обозначается обыкновенно двумя буквами, поставленными у его ребра (двугранный угол АВ). Но если при одном ребре лежат нисколько двугранных углов, то каждый из них обозначают четырьмя буквами, из которых две средние стоят при ребре, а две крайние — у граней (например, двугранный угол SCDR) (черт. 27).

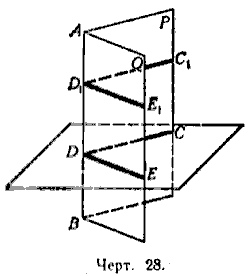
Если из произвольной точки D ребра AB (черт. 28) проведём на каждой грани по перпендикуляру к ребру, то образованный ими угол CDE называется линейным углом двугранного угла.

Величина линейного угла не зависит от положения его вершины на ребре. Так, линейные углы CDE и C₁D₁E₁ равны, потому что их стороны соответственно параллельны и одинаково направлены.

Плоскость линейного угла перпендикулярна к ребру, так как она содержит две прямые, перпендикулярные к нему. Поэтому для получения линейного угла достаточно грани данного двугранного угла пересечь плоскостью, перпендикулярной к ребру, и рассмотреть получившийся в этой плоскости угол.

Видео:Двугранный угол. Признак перпендикулярности плоскостей. Видеоурок 10. Геометрия 10 классСкачать

Равенство и неравенство двугранных углов

Два двугранных угла считаются равными, если они при вложении могут совместиться; в противном случае тот из двугранных углов считается меньшим, который составит часть другого угла.

Подобно углам в планиметрии, двугранные углы могут быть смежные, вертикальные и пр.

Если два смежных двугранных угла равны между собой, то каждый из них называется прямым двугранным углом.

1) Равным двугранным углам соответствуют равные линейные углы.

2) Большему двугранному углу соответствует больший линейный угол.

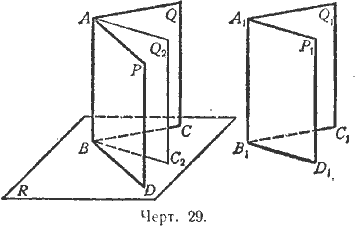
Пусть PABQ, и Р₁А₁В₁Q₁ (черт. 29) — два двугранных угла. Вложим угол А₁В₁ в угол АВ так, чтобы ребро А₁В₁ совпало с ребром AB и грань P₁ с гранью P.

Тогда если эти двугранные углы равны, то грань Q₁ совпадёт с гранью Q; если же угол А₁В₁ меньше угла AB, то грань Q₁ займёт некоторое положение внутри двугранного угла, например Q₂.

Заметив это, возьмём на общем ребре какую-нибудь точку В и проведём через неё плоскость R, перпендикулярную к ребру. От пересечения этой плоскости с гранями двугранных углов получатся линейные углы. Ясно, что если двугранные углы совпадут, то у них окажется один и тот же линейный угол CBD; если же двугранные углы не совпадут, если, например, грань Q₁ займёт положение Q₂, то у большего двугранного угла окажется больший линейный угол (именно: ∠CBD > ∠C₂BD).

1) Равным линейным углам соответствуют равные двугранные углы.

2) Большему линейному углу соответствует больший двугранный угол.

Эти теоремы легко доказываются от противного.

1) Прямому двугранному углу соответствует прямой линейный угол, и обратно.

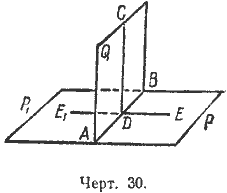
Пусть (черт. 30) двугранный угол PABQ прямой. Это значит, что он равен смежному углу QABP₁. Но в таком случае линейные углы CDE и CDE₁ также равны; а так как они смежные, то каждый из них должен быть прямой. Обратно, если равны смежные линейные углы CDE и CDE₁, то равны и смежные двугранные углы, т.е. каждый из ни должен быть прямой.

2) Bcе прямые двугранные углы равны, потому что у них равны линейные углы.

Подобным же образом легко доказать, что:

3) Вертикальные двугранные углы равны.

4) Двугранные углы с соответственно параллельными и одинаково (или противоположно) направленными гранями равны.

5) Если за единицу двугранных углов возьмём такой двугранный угол, который соответствует единице линейных углов, то можно сказать, чтo двугранный угол измеряется его линейным углом.