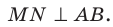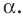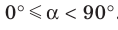Куб его параллельные перпендикулярные скрещивающиеся прямые

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.

Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;

прямая призма, все грани которой есть квадраты;

прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

Видео:10 класс - Геометрия - Скрещивающиеся прямыеСкачать

Элементы куба

Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Вершина

Точки пересечения рёбер называются вершинами. Их число равно восьми.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.

Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Диагональ куба — одна из осей симметрии.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Диагональ грани куба

Длина диагонали грани в √2 раз больше ребра, то есть:

Эта формула доказывается также с помощью теоремы Пифагора.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Объем куба

Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:

Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Периметр куба

Сумма длин всех рёбер равна:

Видео:Перпендикулярные прямые. 6 класс.Скачать

Площадь поверхности

Сумма площадей всех граней называется площадью поверхности куба. Она равна:

Видео:10 класс, 15 урок, Перпендикулярные прямые в пространствеСкачать

Сфера, вписанная в куб

Такая сфера имеет центр, совпадающий с центром куба.

Радиус равен половине ребра:

Видео:Угол между прямыми в пространстве. 10 класс.Скачать

Сфера, описанная вокруг куба

Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:

Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

Координаты вершин куба

В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.

Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:

Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).

Видео:Перпендикулярность прямой и плоскости. 10 класс.Скачать

Свойства куба

Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.

Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.

у куба все грани равны, являются квадратами;

у куба все рёбра равны;

один центр и несколько осей симметрии.

Видео:Геометрия 7 класс (Урок№33 - Повторение. Параллельные и перпендикулярные прямые.)Скачать

Четыре способа решения задач на нахождение расстояния между скрещивающимися прямыми

Разделы: Математика

Среди огромного количества стереометрических задач в учебниках геометрии, в различных сборниках задач, пособиях по подготовке в ВУЗы крайне редко встречаются задачи на нахождение расстояния между скрещивающимися прямыми. Возможно, это обусловлено как узостью их практического применения (относительно школьной программы, в отличие от «выигрышных» задач на вычисление площадей и объемов), так и сложностью данной темы.

Практика проведения ЕГЭ показывает, что многие учащиеся вообще не приступают к выполнению заданий по геометрии, входящих в экзаменационную работу. Для обеспечения успешного выполнения геометрических заданий повышенного уровня сложности необходимо развивать гибкость мышления, способность анализировать предполагаемую конфигурацию и вычленять в ней части, рассмотрение которых позволяет найти путь решения задачи.

Школьный курс предполагает изучение четырех способов решения задач на нахождение расстояния между скрещивающимися прямыми. Выбор способа обусловлен, в первую очередь, особенностями конкретной задачи, предоставленными ею возможностями для выбора, и, во вторую очередь, способностями и особенностями «пространственного мышления» конкретного учащегося. Каждый из этих способов позволяет решить самую главную часть задачи — построение отрезка, перпендикулярного обеим скрещивающимся прямым (для вычислительной же части задач деление на способы не требуется).

Основные способы решения задач на нахождение расстояния между скрещивающимися прямыми

Нахождение длины общего перпендикуляра двух скрещивающихся прямых, т.е. отрезка с концами на этих прямых и перпендикулярного каждой из этих прямых.

Нахождение расстояния от одной из скрещивающихся прямых до параллельной ей плоскости, проходящей через другую прямую.

Нахождение расстояния между двумя параллельными плоскостями, проходящими через заданные скрещивающиеся прямые.

Нахождение расстояния от точки, являющейся проекцией одной из скрещивающихся прямых, на перпендикулярную ей плоскость (так называемый «экран») до проекции другой прямой на ту же самую плоскость.

Проведем демонстрацию всех четырех способов на следующей простейшей задаче: «В кубе с ребром а найти расстояние между любым ребром и диагональю не пересекающей его грани». Ответ: .

h_скр перпендикулярна плоскости боковой грани, содержащей диагональ d и перпендикулярна ребру, следовательно, h_скр и является расстоянием между ребром а и диагональю d.

Плоскость A параллельна ребру и проходит через данную диагональ, следовательно, данная h_скр является не только расстоянием от ребра до плоскости A, но и расстоянием от ребра до данной диагонали.

Плоскости A и B параллельны и проходят через две данные скрещивающиеся прямые, следовательно, расстояние между этими плоскостями равно расстоянию между двумя скрещивающимися прямыми.

Плоскость A перпендикулярна ребру куба. При проекции на A диагонали d данная диагональ обращается в одну из сторон основания куба. Данная h_скр является расстоянием между прямой, содержащей ребро, и проекцией диагонали на плоскость C, а значит и между прямой, содержащей ребро, и диагональю.

Остановимся подробнее на применении каждого способа для изучаемых в школе многогранников.

Применение первого способа достаточно ограничено: он хорошо применяется лишь в некоторых задачах, так как достаточно сложно определить и обосновать в простейших задачах точное, а в сложных — ориентировочное местоположение общего перпендикуляра двух скрещивающихся прямых. Кроме того, при нахождении длины этого перпендикуляра в сложных задачах можно столкнуться с непреодолимыми трудностями.

Задача 1. В прямоугольном параллелепипеде с размерами a, b, h найти расстояние между боковым ребром и не пересекающейся с ним диагональю основания.

Пусть AHBD. Так как А₁А перпендикулярна плоскости АВСD , то А₁А AH.

AH перпендикулярна обеим из двух скрещивающихся прямых, следовательно AH?- расстояние между прямыми А₁А и BD. В прямоугольном треугольнике ABD, зная длины катетов AB и AD, находим высоту AH, используя формулы для вычисления площади прямоугольного треугольника. Ответ:

Задача 2. В правильной 4-угольной пирамиде с боковым ребром L и стороной основания a найти расстояние между апофемой и стороной основания, пересекающей боковую грань, содержащую эту апофему.

SHCD как апофема, ADCD, так как ABCD — квадрат. Следовательно, DH — расстояние между прямыми SH и AD. DH равно половине стороны CD. Ответ:

Применение этого способа также ограничено в связи с тем, что если можно быстро построить (или найти уже готовую) проходящую через одну из скрещивающихся прямых плоскость, параллельную другой прямой, то затем построение перпендикуляра из любой точки второй прямой к этой плоскости (внутри многогранника) вызывает трудности. Однако в несложных задачах, где построение (или отыскивание) указанного перпендикуляра трудностей не вызывает, данный способ является самым быстрым и легким, и поэтому доступен.

Задача 2. Решение уже указанной выше задачи данным способом особых трудностей не вызывает.

Плоскость EFM параллельна прямой AD, т. к AD || EF. Прямая MF лежит в этой плоскости, следовательно, расстояние между прямой AD и плоскостью EFM равно расстоянию между прямой AD и прямой MF. Проведем OHAD. OHEF, OHMO, следовательно, OH(EFM), следовательно, OH — расстояние между прямой AD и плоскостью EFM, а значит, и расстояние между прямой AD и прямой MF. Находим OH из треугольника AOD.

Ответ:

Задача 3. В прямоугольном параллелепипеде с размерами a,b и h найти расстояние между боковым ребром и не пересекающейся с ним диагональю параллелепипеда.

Прямая AA₁ параллельна плоскости BB₁D₁D, B₁D принадлежит этой плоскости, следовательно расстояние от AA₁ до плоскости BB₁D₁D равно расстоянию между прямыми AA₁ и B₁D. Проведем AHBD. Также, AH B₁B, следовательно AH(BB₁D₁D), следовательно AHB₁D, т. е. AH — искомое расстояние. Находим AH из прямоугольного треугольника ABD.

Ответ:

Задача 4. В правильной шестиугольной призме A:F₁ c высотой h и стороной основания a найти расстояние между прямыми:

Рассмотрим плоскость E₁EDD₁. A₁E₁EE₁, A₁E₁E₁D₁, следовательно

A₁E₁ (E₁EDD₁). Также A₁E₁ AA₁. Следовательно, A₁E₁ является расстоянием от прямой AA₁ до плоскости E₁EDD₁. ED₁(E₁EDD₁)., следовательно AE₁ — расстояние от прямой AA₁ до прямой ED₁. Находим A₁E₁ из треугольника F₁A₁E₁ по теореме косинусов. Ответ:

б) AF и диагональю BE₁.

Проведем из точки F прямую FH перпендикулярно BE. EE₁FH, FHBE, следовательно FH(BEE₁B₁), следовательно FH является расстоянием между прямой AF и (BEE₁B₁), а значит и расстоянием между прямой AF и диагональю BE₁. Ответ:

Применение этого способа крайне ограничено, так как плоскость, параллельную одной из прямых (способ II) строить легче, чем две параллельные плоскости, однако способ III можно использовать в призмах, если скрещивающиеся прямые принадлежат параллельным граням, а также в тех случаях, когда в многограннике несложно построить параллельные сечения, содержащие заданные прямые.

а) Плоскости BAA₁B₁ и DEE₁D₁ параллельны, так как AB || ED и AA₁ || EE₁. ED₁DEE₁D₁, AA₁(BAA₁B₁), следовательно, расстояние между прямыми AA₁ и ED₁ равно расстоянию между плоскостями BAA₁B₁ и DEE₁D₁. A₁E₁AA₁, A₁E₁A₁B₁, следовательно, A₁E₁BAA₁B₁. Аналогично доказываем, что A₁E₁(DEE₁D₁). Т.о., A₁E₁ является расстоянием между плоскостями BAA₁B₁ и DEE₁D₁, а значит, и между прямыми AA₁ и ED₁. Находим A₁E₁ из треугольника A₁F₁E₁, который является равнобедренным с углом A₁F₁E₁, равным . Ответ:

б) Расстояние между AF и диагональю BE₁ находится аналогично.

Ответ:.

Задача 5. В кубе с ребром а найти расстояние между двумя непересекающимися диагоналями двух смежных граней.

Данная задача рассматривается как классическая в некоторых пособиях, но, как правило, ее решение дается способом IV, однако является вполне доступной для решения с помощью способа III.

Некоторую трудность в данной задаче вызывает доказательство перпендикулярности диагонали A₁C обеим параллельным плоскостям (AB₁D₁ || BC₁D). B₁CBC₁ и BC₁A₁B₁, следовательно, прямая BC₁ перпендикулярна плоскости A₁B₁C, и следовательно, BC₁A₁C. Также, A₁CBD. Следовательно, прямая A₁C перпендикулярна плоскости BC₁D. Вычислительная же часть задачи особых трудностей не вызывает, так как h_скр = EF находится как разность между диагональю куба и высотами двух одинаковых правильных пирамид A₁AB₁D₁ и CC₁BD.

Ответ:

Данный способ имеет достаточно широкое применение. Для задач средней и повышенной трудности его можно считать основным. Нет необходимости применять его только тогда, когда один из трех предыдущих способов работает проще и быстрее, так как в таких случаях способ IV может только усложнить решение задачи, или сделать его труднодоступным. Данный способ очень выгодно использовать в случае перпендикулярности скрещивающихся прямых, так как нет необходимости построения проекции одной из прямых на «экран»

Задача 5. Все та же «классическая» задача (с непересекающимися диагоналями двух смежных граней куба) перестает казаться сложной, как только находится «экран» — диагональное сечение куба.

Рассмотрим плоскость A₁B₁CD. C₁F (A₁B₁CD), т. к. C₁FB₁C и C₁FA₁B₁. Тогда проекцией C₁D на «экран» будет являться отрезок DF. Проведем EMDF. Отрезок EM и будет являться расстоянием между двумя непересекающимися диагоналями двух смежных граней. Находим EM из прямоугольного треугольника EDF. Ответ:.

Задача 6. В правильной треугольной пирамиде найти расстояние и угол между скрещивающимися прямыми: боковым ребром l и стороной основания a.

В данной и аналогичных ей задачах способ IV быстрее других способов приводит к решению, так как построив сечение, играющее роль «экрана», перпендикулярно AC (треугольник BDM), видно, что далее нет необходимости строить проекцию другой прямой (BM) на этот экран. DH — искомое расстояние. DH находим из треугольника MDB, используя формулы площади. Ответ: .

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Перпендикулярность в пространстве с примерами решения

Содержание:

Видео:Расстояние между скрещивающимися прямыми за 1 минуту. #математикапрофиль2023 #егэ2023 #школа #fypСкачать

Перпендикулярность в пространстве

В этом параграфе вы ознакомитесь с понятиями угла между прямыми в пространстве, угла между прямой и плоскостью, угла между двумя плоскостями; узнаете, что такое ортогональная проекция, изучите свой­ство ортогональной проекции многоугольника.

Угол между прямыми в пространстве

Поскольку две любые пересекающиеся прямые пространства лежат в одной плоскости, то угол между ними определим так же, как в планиметрии. Определение. Углом между двумя пересекающимися прямыми называют величину того из углов, образовавшихся при их пересечении, который не превышает (рис. 33.1).

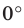
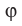
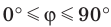
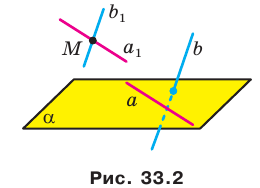
Угол между двумя параллельными прямыми считают равным Следовательно, если — угол между двумя прямыми, лежащими в одной плоскости, то .

Введем понятие угла между скрещивающимися прямыми. Определение. Углом между двумя скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся пря­мым.

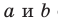
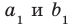
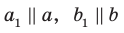
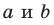
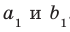
Пусть прямые скрещивающиеся. Через точку М простран­ства проведем прямые так, что (рис. 33.2). По определению угол между скрещивающимися прямыми равен углу между пересекающимися прямыми .

Возникает естественный вопрос: зависит ли угол между данными скрещивающимися прямыми 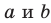от выбора точки М ? Ответить на этот вопрос помогает следующая теорема.

Теорема 33.1. Угол между двумя пересекающимися прямыми равен углу между двумя другими пересекающимися прямыми, соответственно параллельными данным.

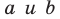
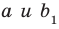
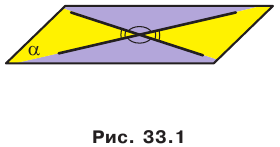
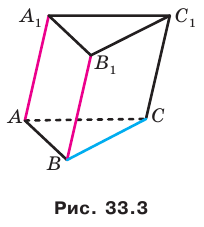
Воспользовавшись теоремой 33.1, можно показать, что угол между скрещивающимися прямыми равен углу между пересекающимися прямыми , где

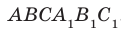
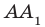
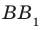
Например, на рисунке 33.3 изображена треугольная призма . Угол между скрещивающимися прямыми и ВС равен углу между пересекающимися прямыми и ВС.

Определение. Две прямые в пространстве называют перпендикулярными, если угол между ними равен 90°.

Заметим, что перпендикулярные прямые могут как пересекаться, так и быть скрещивающимися.

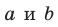
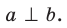
Если прямые перпендикулярны, то записывают: Два отрезка в пространстве называют перпендикулярными, если они лежат на перпендикулярных прямых.

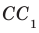
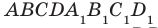
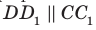
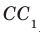
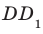
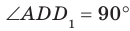
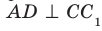
Например, ребра AD и куба перпендикулярны (рис. 33.4). Действительно, поскольку то угол между прямыми AD и равен углу между прямыми AD и . Но , поэтому .

Пример:

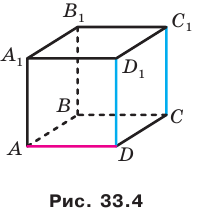
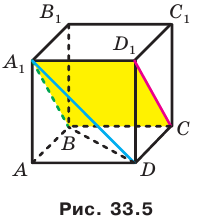
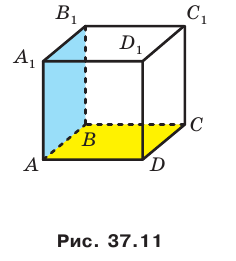
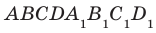
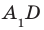
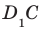
На рисунке 33.5 изображен куб . Най­дите угол между прямыми и .

Решение:

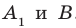
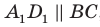
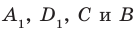
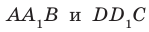
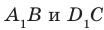
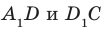
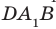
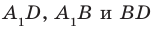
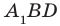
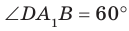
Соединим точки . Поскольку , то точки лежат в одной плоскости. Эта плоскость пересекает параллельные плоскости по параллельным прямым . Следовательно, угол между прямыми равен углу . Соединим точки В и D. Отрезки равны как диагонали равных квадратов. Следовательно, треугольник равносторонний. Тогда . Ответ : 60°.

Перпендикулярность прямой и плоскости

В повседневной жизни мы говорим: флагшток перпендикулярен поверхности земли (рис. 34.1), мачты парусника перпендикулярны поверхности палубы (рис. 34.2), шуруп вкручивают в доску перпендикулярно ее поверхности (рис. 34.3) и т.п.

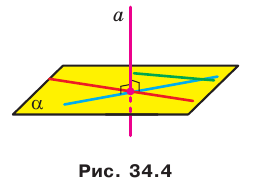
Эти примеры дают представление о прямой, перпендикулярной плоскости. Определение. Прямую называют перпендикулярной пло­скости, если она перпендикулярна любой прямой, лежащей в этой плоскости (рис. 34.4).

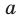
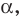
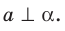
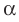
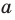
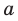
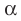
Если прямая перпендикулярна плоскости то записывают: Также принято говорить, что плоскость перпендикулярна прямой или прямая и плоскость перпендикулярны.

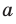
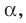
Из определения следует, что если прямая перпендикулярна плоскости то она пересекает эту плоскость.

Отрезок называют перпендикулярным плоскости, если он принадлежит прямой, перпендикулярной этой плоскости.

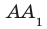
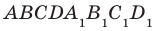
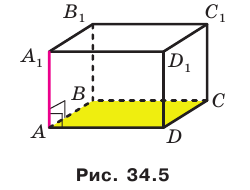
Например, интуитивно понятно, что ребро прямоугольного параллелепипеда перпендикулярно плоскости АВС (рис. 34.5). Доказать этот факт нетрудно, воспользовавшись следующей теоремой.

Теорема 34.1 (признак перпендикулярности прямой и плоскости). Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна самой плоскости.

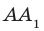
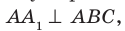
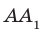
На рисунке 34.5 прямая перпендикулярна двум пересекающимся прямым АВ и AD плоскости АВС. Следовательно, по признаку перпен­дикулярности прямой и плоскости а значит, и ребро также перпендикулярно плоскости АВС.

Теорему 34.1 часто используют на практике. Например, подставка для новогодней елки имеет форму крестовины. Если елку установить так, чтобы ее ствол был перпендикулярен направлениям крестовины, то елка будет стоять перпендикулярно плоскости пола (рис. 34.6).

Приведем теорему, которую можно рассматривать как еще один признак перпендикуляр­ности прямой и плоскости.

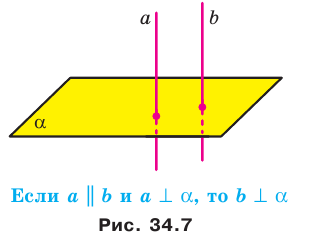
Теорем а 34.2. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости (рис. 34.7).

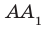
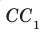
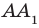
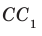
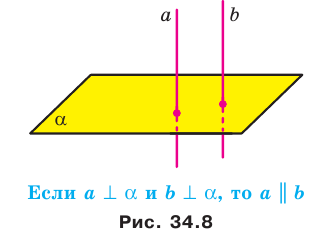
Например, на рисунке 34.5 прямая перпендикулярна плоскости АВС, а прямая параллельна прямой . Следовательно, по теореме 34.2 прямая также перпендикулярна плоскости АВС. Сформулируем теорему, являющуюся признаком параллельности двух прямых.

Теорем а 34.3. Если две прямые перпендикулярны одной и той же плоскости, то они параллельны (рис. 34.8). Справедлива и такая теорема.

Теорема 34.4. Через данную точку можно провести прямую, перпендикулярную данной плоскости, и притом только одну.

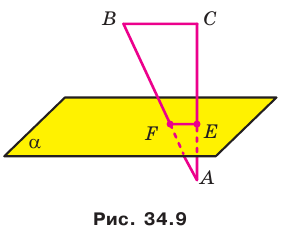
Пример:

Плоскость 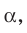перпендикулярная катету АС прямоугольного треугольника АВС, пересекает катет АС в точке Е, а ги­потенузу АВ — в точке F (рис. 34.9). Найдите отрезок EF, если АЕ : ЕС = 3 : 4, ВС = 21 см.

Решение:

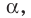
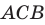
Поскольку прямая АС перпендикулярна плоскости то прямая АС перпендикулярна любой прямой этой плоскости, в частности прямой EF. Прямые EF и ВС лежат в одной плоскости и перпендикулярны прямой АС, поэтому . Из этого следует, что треугольники AEF и подобны. Следовательно, можно записать: EF : СВ=АЕ : АС. Отсюда EF : 21 = 3 : 7, EF = 9 см. Ответ: 9 см.

Перпендикуляр и наклонная

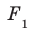
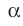
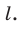
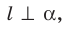
Пусть фигура — параллельная проекция фигуры F на плоскость в направлении прямой Если , то фигуру называют ортогональной проекцией фигуры F на плоскость

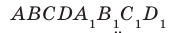
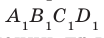
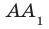
Например, основание ABCD прямоугольного параллелепипеда является ортогональной проекцией основания на пло­скость АВС в направлении прямой (рис. 35.1).

В дальнейшем, говоря о проекции фигуры, если не оговорено противное, будем иметь в виду ортогональную проекцию.

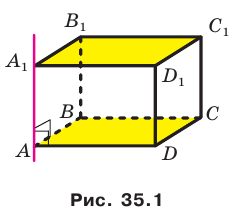
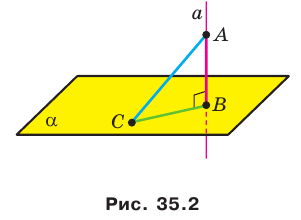
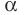
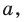
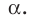
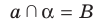
Пусть даны плоскость и не принадлежащая ей точка А . Через точку А проведем прямую перпендикулярную плоскости Пусть (рис. 35.2).

Отрезок АВ называют перпендикуляром, опущенным из точки А на плоскость точку В — основанием перпендикуляра. Основание В перпендикуляра АВ — это проекция точки А на плоскость .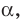

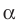
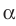
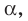
Отметим на плоскости какую-нибудь точку С, отличную от точки В. Проведем отрезок АС (рис. 35.2). Отрезок АС называют наклонной, проведенной из точки А к плоскости точку С — основанием наклонной. Отрезок ВС является проекцией наклонной АС.

Теорема 35.1. Если из одной тонки проведены к плоскости перпендикуляр и наклонная, то наклонная больше перпендикуляра.

Пример:

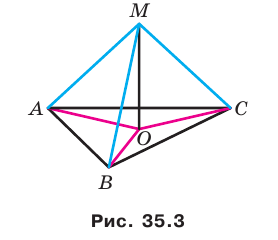
Докажите, что если точка, не принадлежащая плоскости многоугольника, равноудалена от его вершин, то проекцией этой точки на плоскость многоугольника является центр его описанной окружности.

Решение:

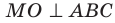
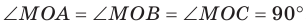
Проведем доказательство для треугольника. Для других многоугольников доказательство будет аналогичным. Пусть точка М не принадлежит плоскости АВС, причем МА = = МВ = МС. Опустим из точки М перпендикуляр МО на плоскость АВС (рис. 35.3). Докажем, что точка О — центр описанной окружности треугольника АВС. Поскольку , то . В пря­моугольных треугольниках МОА, МОВ, МОС катет МО — общий, гипотенузы равны, следовательно, эти треугольники равны по гипотенузе и катету. Из равенства данных треугольников следует, что ОА = ОВ = ОС, то есть точка О — центр описанной окружности треугольника АВС.

Заметим, что когда надо определить расстояние между двумя геометрическими фигурами, то стремятся найти расстояние между их ближайшими точками. Например, из курса планиметрии вы знаете, что расстоянием от точки, не принадлежащей прямой, до этой прямой называют расстояние от данной точки до ближайшей точки на прямой, то есть длину перпендикуляра, опущенного из точки на прямую. Теорема 35.1 показывает, что целесообразно принять следующее определение.

Определение. Если точка не принадлежит плоскости, то рас­стоянием от точки до плоскости называют длину перпен­дикуляра, опущенного из точки на плоскость. Если точка принадлежит плоскости, то считают, что расстояние от точки до плоскости равно нулю.

Пример:

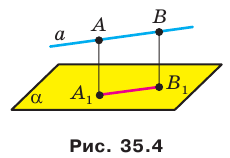
Докажите, что если прямая параллельна плоскости, то все точки прямой равноудалены от плоскости.

Решение:

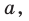
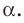
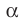
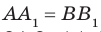
Пусть А и В — две произвольные точки прямой параллельной плоскости Точки — основания перпендикуляров, опущенных соответственно из точек А и В на плоскость (рис. 35.4). Докажем, что .

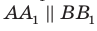
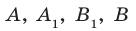
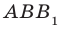
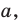
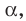
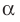
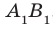
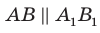
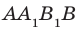
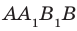
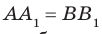
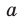
По теореме 34.3 . Следовательно, точки лежат в одной пло­скости. Плоскость проходит через прямую параллельную плоскости и пересекает плоскость по прямой . Тогда по теореме 30.2 получаем: . Таким образом, в четырехугольнике каждые две противолежащие стороны параллельны. Следовательно, четырехугольник — параллелограмм. Отсюда Так как точки А и В выбраны на прямой произвольно, то утверждение задачи доказано.

Доказанное свойство позволяет принять следующее определение. Определение. Расстоянием от прямой до параллель­ной ей плоскости называют расстояние от любой точки этой прямой до плоскости. Используя результат, полученный в ключевой задаче 2, можно решить следующую задачу.

Пример:

Докажите, что если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости. Определение. Расстоянием между двумя параллель­ными плоскостями называют расстояние от любой точки одной плоскости до другой плоскости.

Результаты, полученные в ключевых задачах 2 и 3, часто ис­пользуют в практической деятельности, например в строительстве (рис. 35.5).

Теорема 35.2 (теорема о трех перпендикулярах). Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной. И наоборот, если прямая, принадлежащая плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и проекции наклонной на эту плоскость.

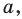
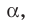
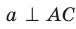
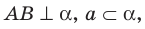
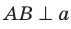
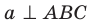
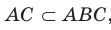
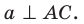
Доказательство. Докажем первую часть теоремы.Пусть прямая принадлежащая плоскости перпендикулярна проекции ВС наклонной АС (рис. 35.6). Докажем, что . Имеем: следовательно, . Получили, что прямая а перпендикулярна двум пересекающимся прямым АВ и ВС плоскости АВС; следовательно,. Поскольку то Доказательство второй части теоремы аналогично доказатель­ству первой части.

Пример:

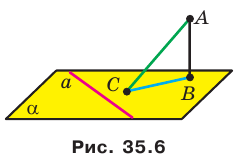
Точка М не принадлежит плоскости выпуклого многоугольника и равноудалена от всех прямых, содержащих его стороны. Проекцией точки М на плоскость многоугольника является точка О, принадлежащая многоугольнику. Докажите, что точка О — центр вписанной окружности многоугольника.

Решение:

Проведем доказательство для треугольника. Для других многоугольников доказательство будет аналогичным. Опустим из точки О перпендикуляры ON, ОК и ОЕ соответственно на прямые АВ, ВС и СА (рис. 35.7). Соединим точку М с точками Е, К и N.

Отрезок ON является проекцией на­клонной MN на плоскость АВС. По построению 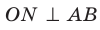. Тогда по теореме о трех перпендикулярах получаем:

Аналогично можно доказать, что 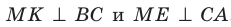. Следовательно, длины отрезков MN, МК и ME — расстояния от точки М до прямых АВ, ВС и СА соответственно. По условию MN = МК = МЕ.

В прямоугольных треугольниках MON, МОК, МОЕ катет МО общий, гипотенузы равны; следовательно, данные треугольники равны по катету и гипотенузе. Из равенства этих треугольников следует, что ON = ОК = ОЕ.

Длины отрезков ON, ОК и ОЕ являются расстояниями от точки О до прямых, содержащих стороны треугольника АВС. Мы показали, что эти расстояния равны. Так как точка О принадлежит треугольнику АВС, то точка О — центр вписанной окружности треугольника АВС.

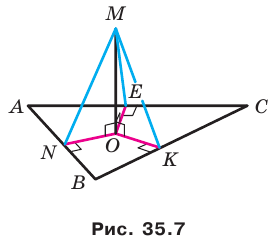
Угол между прямой и плоскостью

Вы знаете, что в давние времена путешественники ориентировались по звездам. Они измеряли угол, который образовывал с плоскостью горизонта луч, идущий от данной точки к небесному телу.

Сегодня человеку в своей деятельности также важно определять углы, под которыми наклонены к данной плоскости некоторые объекты (рис. 36.1). Эти примеры показывают, что целесообразно ввести понятие угла между прямой и плоскостью.

Определение. Если прямая параллельна плоскости или принадлежит ей, то считают, что угол меж ду такой прямой и плоскостью равен 0°.

Если прямая перпендикулярна плоскости, то считают, что угол между такой прямой и плоскостью равен .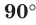

Если прямая пересекает плоскость и не перпендикулярна ей, то углом между такой прямой и плоскостью называют угол между прямой и ее проекцией на плоскость (рис. 36.2).

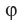
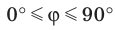
Из определения следует, что если — угол между прямой и плоскостью, то .

Также принято говорить, что прямая образует угол 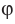с плоскостью.

Углом между отрезком и плоскостью называют угол между прямой, содержащей этот отрезок, и плоскостью.

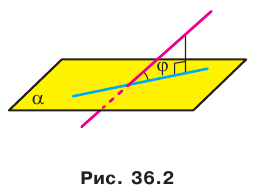
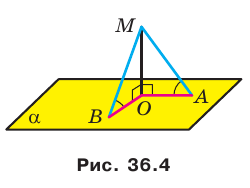
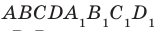
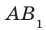
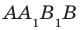
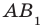
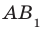
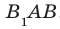
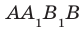
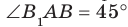
Например, рассмотрим куб (рис. 36.3). Угол между диагональю грани и плоскостью АВС равен 45°. Действительно, прямая АВ — проекция прямой на плоскость АВС. Тогда угол между прямой и плоскостью АВС равен величине угла . Поскольку четырехугольник — квадрат, то .

Пример:

Докажите, что если из одной точки к плоскости проведены наклонные, образующие равные углы с плоскостью, то проекция данной точки на плоскость равноудалена от оснований наклонных.

Решение:

Пусть МЛ и М В — наклонные, образующие с плоскостью 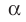равные углы, отрезки ОА и ОВ — проекции этих наклонных (рис. 36.4). Докажем, что ОА = ОВ.

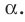
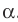
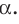
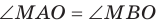
Прямая ОА является проекцией прямой МА на плоскость Так как угол МАО острый, то он равен углу между прямыми ОА и МА. Следовательно, величина угла МАО равна углу между наклонной МА и плоскостью . Аналогично можно доказать, что величина угла МВО равна углу между наклонной МВ и плоскостью По условию .

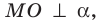
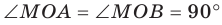
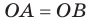
Поскольку то . Получаем, что прямоугольные треугольники МОА и МОВ равны по катету и противолежащему острому углу. Отсюда .

Двугранный угол. Угол между плоскостями

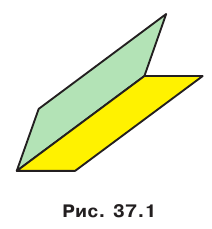
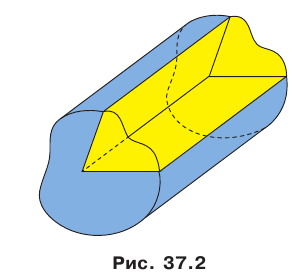
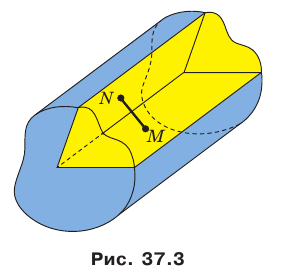
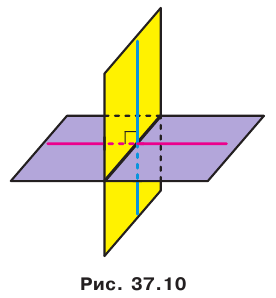
На рисунке 37.1 изображена фигура, состоящая из двух полуплоскостей, имеющих общую границу. Эта фигура делит пространство на две части, выделенные на рисунке 37.2 разными цветами. Каждую из этих частей вместе с полуплоскостями называют двугран­ным углом. Полуплоскости называют гранями двугранного угла, а их общую границу — ребром двугранного угла. Как видим, «желтый» и «синий» двугранные углы, изображенные на рисунке 37.2, существенно различаются. Это различие выражается следующим свойством. На гранях двугранного угла выберем произвольные точки М и N (рис. 37.3).

Отрезок MN принадлежит «желтому» двугранному углу, а «сине­му» двугранному углу принадлежат лишь концы отрезка. В дальнейшем, говоря «двугранный угол», будем подразумевать такой двугранный угол, который содержит любой отрезок с концами на его гранях («желтый» двугранный угол).

Наглядное представление о двугранном угле дают полуоткрытая классная доска, двускатная крыша, открытый ноутбук (рис. 37.4).

Двугранный угол считают пространственным аналогом угла на плоскости. Вы знаете, как определяют величину угла на плоскости. Научимся определять величину двугранного угла.

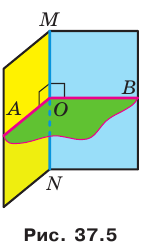
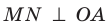
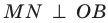
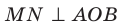
Отметим на ребре MN двугранного угла произ­вольную точку О. Через точку О в гранях двугран­ного угла проведем лучи ОА и ОВ перпендикулярно ребру MN (рис. 37.5). Угол АОВ, образованный этими лучами, называют линейным углом двугран­ного угла. Поскольку и , то . Таким образом, если через произвольную точку ребра двугранного угла провести плоскость перпендикулярно ребру, то эта плоскость пересечет двугранный угол по его линейному углу.

Определение. Величиной двугранного угла называют величину его линейного угла.

Двугранный угол называют острым, прямым, тупым или развернутым, если его линейный угол соответственно острый, прямой, тупой или развернутый.

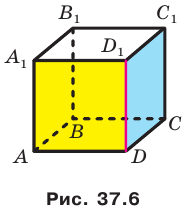
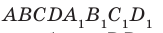
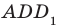
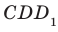
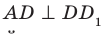
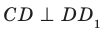
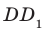
Например, рассмотрим куб (рис. 37.6). Двугранный угол с ребром , грани которого принадлежат плоскостям и является прямым. Действительно, поскольку и , то угол ADC — линейный угол двугранного угла с ребром .

Угол ADC прямой.

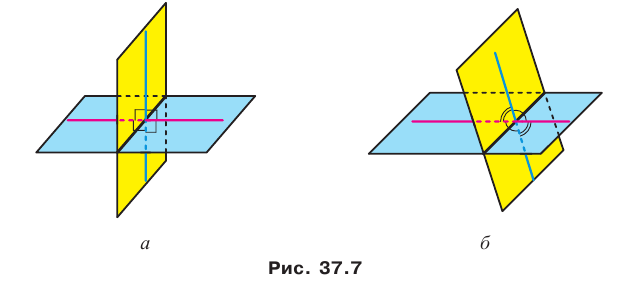
При пересечении двух плоскостей образуются четыре двугранных угла, отличных от развернутого (рис. 37.7). Здесь возможны два случая:

1. все четыре двугранных угла прямые (рис. 37.7, а);
2. из четырех двугранных углов два равных угла острые и два равных угла тупые (рис. 37.7, б).

В обоих случаях из четырех двугранных углов найдется такой, величина которого не превышает 90°.

Определение. Углом между двумя пересекающимися плоскостями называют величину того из образовавшихся дву­гранных углов, который не превышает 90°. Угол между двумя параллельными плоскостям и равен 0°.

Углом между многоугольником и плоскостью, которой много угольник не принадлежит, называют угол между плоскостью, содержащей многоугольник, и данной плоскостью.

Углом между двумя многоугольниками, лежащими в разных плоскостях, называют угол между плоскостями, в которых лежат эти многоугольники.

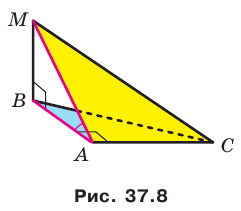
Пример:

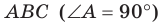
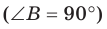
Прямоугольные треугольники и АВМ имеют общий катет АВ (рис. 37.8). Отрезок МВ перпендикулярен плоскости АВС. Известно, что МВ = 4 см, АС = 6 см, МС = 10 см. Найдите угол между плоскостями АВС и АМС.

Решение:

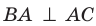
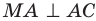
Отрезок ВА является проекцией наклонной МА на плоскость АВС. Так как , то по теореме о трех перпендикулярах . Следователь но, угол МАВ — линейный угол двугранного угла с ребром АС, грани которого принадлежат плоскостям АВС и АМС. Поскольку угол МАВ острый, то угол между плоскостями АВС и АМС равен величине угла МАВ.

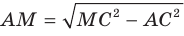
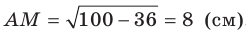
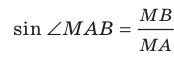
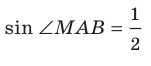
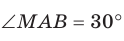
Для стороны AM прямоугольного треугольника АМС можно записать: . Отсюда . Для угла МАВ прямоугольного треугольника МАВ запишем: . Отсюда и . Ответ: 30°.

Имеет место теорема, устанавливающая связь между площадью данного многоугольника и площадью его проекции.

Теорема 37.1 (площадь ортогональной проекции мно­гоугольника). Площадь проекции выпуклого многоугольника равна произведению его площади и косинуса угла а между многоугольником и его проекцией, где .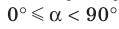

Определение. Две плоскости называют перпендикулярными, если угол между ними равен 90°.

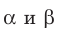
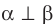
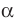
Если плоскости перпендикулярны, то записывают: . Также принято говорить, что плоскость перпендикулярна плоскости или плоскость перпендикулярна плоскости .

Наглядное представление о перпендикулярных плоскостях дают плоскости стены и потолка комнаты, плоскости двери и пола, плоскости сетки и теннисного корта (рис. 37.9).

Очевидно, что перпендикулярные плоскости при пересечении образуют четыре прямых двугранных угла (рис. 37.10).

Теорема 37.2 (признак перпендикулярности плоско­стей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

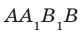
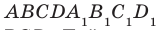
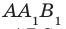
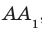
Например, плоскость грани прямоугольного параллелепипеда , (рис. 37.11) перпендикулярна плоскости грани ABCD. Действительно, плоскость проходит через прямую , перпендикулярную плоскости АВС.

ГЛАВНОЕ В ПАРАГРАФЕ 5

Угол между прямыми в пространстве Углом между двумя пересекающимися прямыми называют ве­личину того из углов, образовавшихся при их пересечении, который не превышает 90°. Считают, что угол между двумя параллельными прямыми равен 0°. Углом между двумя скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым. Две прямые в пространстве называют перпендикулярными, если угол между ними равен 90°.

Перпендикулярность прямой и плоскости

• Прямую называют перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
• Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна самой плоскости.
• Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
• Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
• Через данную точку можно провести прямую, перпендикулярную данной плоскости, и притом только одну.

Ортогональная проекция фигуры

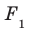
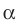
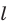
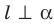
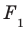
Пусть фигура — параллельная проекция фигуры F на плоскость в направлении прямой . Если , то фигуру называют ортогональной проекцией фигуры F на плоскость

Расстояние от точки до плоскости

Если точка не принадлежит плоскости, то расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из точки на плоскость. Если точка принадлежит плоскости, то считают, что расстояние от точки до плоскости равно нулю.

Расстояние от прямой до параллельной ей плоскости

Расстоянием от прямой до параллельной ей плоскости называют расстояние от любой точки этой прямой до плоскости.

Расстояние между двумя параллельными плоскостями

Расстоянием между двумя параллельными плоскостями назы­вают расстояние от любой точки одной плоскости до другой плоскости.

Теорема о трех перпендикулярах

Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной. И наоборот, если прямая, принадлежащая плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и проекции наклонной на эту плоскость.

Угол между прямой и плоскостью

• Если прямая параллельна плоскости или принадлежит ей, то считают, что угол между такой прямой и плоскостью равен 0°.
• Если прямая перпендикулярна плоскости, то считают, что угол между такой прямой и плоскостью равен 90°.
• Если прямая пересекает плоскость и не перпендикулярна ей, то углом между такой прямой и плоскостью называют угол между прямой и ее проекцией на плоскость.

Величина двугранного угла

Величиной двугранного угла называют величину его линейного угла.

Угол между двумя пересекающимися плоскостями

Углом между двумя пересекающимися плоскостями называют величину того из образовавшихся двугранных углов, который не превышает 90°.

Площадь ортогональной проекции многоугольника

Площадь проекции выпуклого многоугольника равна произведению его площади и косинуса угла а между многоугольником и его проекцией, где

Перпендикулярные плоскости

Две плоскости называют перпендикулярными, если угол между ними равен 90°.

Признак перпендикулярности плоскостей

Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

• Векторы и координаты в пространстве
• Множества
• Рациональные уравнения
• Рациональные неравенства и их системы
• Предел числовой последовательности
• Предел и непрерывность числовой функции одной переменной
• Функции, их свойства и графики
• Параллельность в пространстве

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

🔥 Видео

Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Перпендикулярность прямых в пространстве. 10 класс.Скачать

7. Скрещивающиеся прямыеСкачать

Угол между прямыми в пространстве. Практическая часть. 10 класс.Скачать

Скрещивающиеся прямыеСкачать

Параллельность прямой и плоскости. 10 класс.Скачать

Как провести множество параллельных или перпендикулярных прямых без транспортира?Скачать

Тема ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕСкачать

Параллельные и перпендикулярные прямые.Скачать