Номер рисунка выбирается по последней цифре варианта, а номер условия в таблице — по предпоследней цифре варианта.
Например: вариант 27
номер схемы — 7
номер условия — 2
Задача К3
Прямоугольная пластина (рис. КЗ.0 – К3.5) или круглая пластина радиуса R = 60 см (рис. К3.6 — К3.9) вращается вокруг неподвижной оси с постоянной угловой скоростью , заданной в табл. КЗ (при знаке минус направление противоположно показанному на рисунке). Ось вращения на рис. 0 – 3 и 8, 9 перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 4 – 7 ось вращения ОО1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD (рис. 0 – 5) или по окружности радиуса R, т. е. по ободу пластины (рис. 6 – 9), движется точка М. Закон ее относительного движения, выражаемый уравнением s = AM = f (t) (s – в сантиметрах, t – в секундах), задан в табл. КЗ отдельно для рис. 0 – 5 и для рис. 6 – 9, при этом на рис.6 – 9 s = и отсчитывается по дуге окружности; там же даны размеры b и . На всех рисунках точка М показана в положении, при котором s = AM > 0 (при s
- Сложное движение точки. Пример решения задачи
- Условие задачи
- Решение задачи
- Определение положения точки
- Определение абсолютной скорости точки
- Определение относительной скорости точки
- Определение переносной скорости точки
- Определение абсолютной скорости точки
- Определение абсолютного ускорения точки
- Определение относительного ускорения
- Определение переносного ускорения
- Определение кориолисова ускорения
- Определение абсолютного ускорения
- Абсолютного ускорения точки
- 💡 Видео
Видео:Вращение тела вокруг неподвижной осиСкачать

Сложное движение точки. Пример решения задачи
Теория, применяемая для решения приведенной ниже задачи, излагается на странице “Сложное движение точки, теорема Кориолиса”.
Видео:Физика - движение по окружностиСкачать

Условие задачи
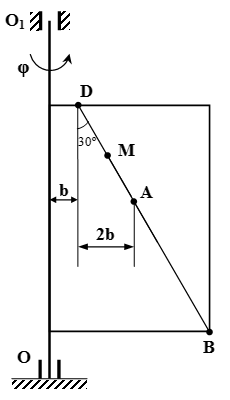
Прямоугольная пластина вращается вокруг неподвижной оси по закону φ = 6 t 2 – 3 t 3 . Положительное направление отсчета угла φ показано на рисунках дуговой стрелкой. Ось вращения OO 1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD движется точка M . Задан закон ее относительного движения, т. е. зависимость s = AM = 40( t – 2 t 3 ) – 40 ( s — в сантиметрах, t — в секундах). Расстояние b = 20 см . На рисунке точка M показана в положении, при котором s = AM > 0 (при s 0 точка M находится по другую сторону от точки A ).
Найти абсолютную скорость и абсолютное ускорение точки M в момент времени t 1 = 1 с .
Указания. Эта задача – на сложное движение точки. Для ее решения необходимо воспользоваться теоремами о сложении скоростей и о сложении ускорений (теорема Кориолиса). Прежде чем производить все расчеты, следует по условиям задачи определить, где находится точка M на пластине в момент времени t 1 = 1 с , и изобразить точку именно в этом положении (а не в произвольном, показанном на рисунке к задаче).
Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Решение задачи
Дано: b = 20 см , φ = 6 t 2 – 3 t 3 , s = |AM| = 40( t – 2 t 3 ) – 40 , t 1 = 1 c .
Определение положения точки
Определяем положение точки в момент времени t = t 1 = 1 c .
s = 40( t 1 – 2 t 1 3 ) – 40 = 40(1 – 2·1 3 ) – 40 = –80 см.
Поскольку s 0 , то точка M ближе к точке B, чем к D.
|AM| = |–80| = 80 см.
Делаем рисунок.
Определение абсолютной скорости точки
Согласно теореме о сложении скоростей, абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Определение относительной скорости точки
Определяем относительную скорость . Для этого считаем, что пластина неподвижна, а точка M совершает заданное движение. То есть точка M движется по прямой BD . Дифференцируя s по времени t , находим проекцию скорости на направление BD :
.
В момент времени t = t 1 = 1 с ,
см/с.
Поскольку , то вектор направлен в направлении, противоположном BD . То есть от точки M к точке B . Модуль относительной скорости
vот = 200 см/с .
Изображаем вектор на рисунке.
Определение переносной скорости точки
Определяем переносную скорость . Для этого считаем, что точка M жестко связана с пластиной, а пластина совершает заданное движение. То есть пластина вращается вокруг оси OO1. Дифференцируя φ по времени t , находим угловую скорость вращения пластины:
.
В момент времени t = t 1 = 1 с ,
.
Поскольку 0″ style=»width:48px;height:18px;vertical-align:-10px;background-position:-583px -267px»> , то вектор угловой скорости направлен в сторону положительного угла поворота φ , то есть от точки O к точке O1. Модуль угловой скорости:
ω = 3 с -1 .
Изображаем вектор угловой скорости пластины на рисунке.
Из точки M опустим перпендикуляр HM на ось OO1.
При переносном движении точка M движется по окружности радиуса |HM| с центром в точке H .
|HM| = |HK| + |KM| = 3 b + |AM| sin 30° = 60 + 80·0,5 = 100 см ;
Переносная скорость:
vпер = ω|HM| = 3·100 = 300 см/с .
Вектор направлен по касательной к окружности в сторону вращения.
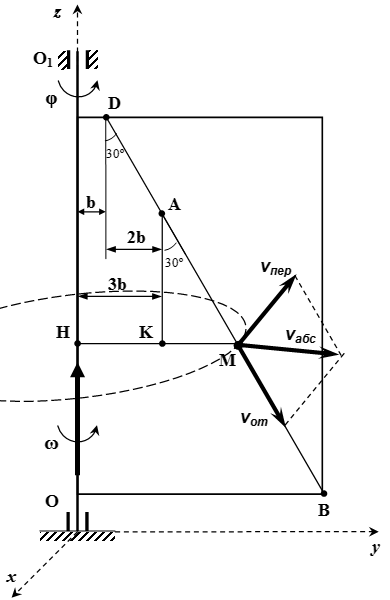
Определение абсолютной скорости точки
Определяем абсолютную скорость . Абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Проводим оси неподвижной системы координат Oxyz . Ось z направим вдоль оси вращения пластины. Пусть в рассматриваемый момент времени ось x перпендикулярна пластине, ось y лежит в плоскости пластины. Тогда вектор относительной скорости лежит в плоскости yz . Вектор переносной скорости направлен противоположно оси x . Поскольку вектор перпендикулярен вектору , то по теореме Пифагора, модуль абсолютной скорости:
.
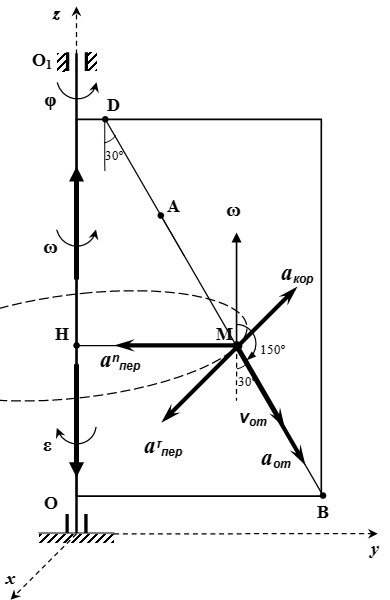
Определение абсолютного ускорения точки
Согласно теореме о сложении ускорений (теорема Кориолиса), абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова ускорений:
,
где
– кориолисово ускорение.
Определение относительного ускорения
Определяем относительное ускорение . Для этого считаем, что пластина неподвижна, а точка M совершает заданное движение. То есть точка M движется по прямой BD . Дважды дифференцируя s по времени t , находим проекцию ускорения на направление BD :
.
В момент времени t = t 1 = 1 с ,
см/с 2 .
Поскольку , то вектор направлен в направлении, противоположном BD . То есть от точки M к точке B . Модуль относительного ускорения
aот = 480 см/с 2 .
Изображаем вектор на рисунке.
Определение переносного ускорения
Определяем переносное ускорение . При переносном движении точка M жестко связана с пластиной, то есть движется по окружности радиуса |HM| с центром в точке H . Разложим переносное ускорение на касательное к окружности и нормальное ускорения:
.
Дважды дифференцируя φ по времени t , находим проекцию углового ускорения пластины на ось OO 1 :
.
В момент времени t = t 1 = 1 с ,
с –2 .
Поскольку , то вектор углового ускорения направлен в сторону, противоположную положительного угла поворота φ , то есть от точки O1 к точке O. Модуль углового ускорения:
ε = 6 с -2 .
Изображаем вектор углового ускорения пластины на рисунке.
Переносное касательное ускорение:
a τ пер = ε |HM| = 6·100 = 600 см/с 2 .
Вектор направлен по касательной к окружности. Поскольку вектор углового ускорения направлен в сторону, противоположную положительного угла поворота φ , то направлен в сторону, противоположную положительному направлению поворота φ . То есть направлен в сторону оси x .
Переносное нормальное ускорение:
a n пер = ω 2 |HM| = 3 2 ·100 = 900 см/с 2 .
Вектор направлен к центру окружности. То есть в сторону, противоположную оси y .
Определение кориолисова ускорения
Кориолисово (поворотное) ускорение:
.
Вектор угловой скорости направлен вдоль оси z . Вектор относительной скорости направлен вдоль прямой |DB| . Угол между этими векторами равен 150° . По свойству векторного произведения,
.
Направление вектора определяется по правилу буравчика. Если ручку буравчика повернуть из положения в положение , то винт буравчика переместится в направлении, противоположном оси x .
Определение абсолютного ускорения
Абсолютное ускорение:
.
Спроектируем это векторное уравнение на оси xyz системы координат.
;
;
.
Модуль абсолютного ускорения:
.
Абсолютная скорость ;
абсолютное ускорение .
Автор: Олег Одинцов . Опубликовано: 10-01-2016
Видео:Центростремительное ускорение. 9 класс.Скачать

Абсолютного ускорения точки
Дано:прямоугольная пластина (рис. К 4.0 – К 4.4) или круглая пластина радиуса R = 60 см (рис. К 4.5 – К 4.9) вращается вокруг неподвижной оси по закону φ=f1(t), заданному в табл. К — 4. Положительное направление отсчета угла показано на рисунках дуговой стрелкой. На рис. 0,1,2,5,6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 3,4.7,8,9 ось вращения ОО1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD (рис. К3.0 — К3.4) или по окружности радиуса R (рис. К3.5 – К3.9) движется точка М; закон ее относительного движения, то есть зависимость s=AM=f2(t) (s — в сантиметрах, t – в секундах), задан в таблице отдельно для рис. К4.0 – К4.4 и для рис. К4.5 – К4.9; там же даны размеры а и h. На рисунках точка М показана в положении, при котором s=AM ›0 (при s‹0 точка М находится по другую сторону от точки А).
Определить:абсолютную скорость и абсолютное ускорение точки М в момент времени t1 =1 c.
Указания: для решения задачи необходимо воспользоваться теоремами о сложении скоростей и ускорений. Прежде чем производить расчеты, следует определить, где находится точка на пластине в момент времени t1 =1 c и изобразить точку именно в этом положении.
4.4.3. Пример К– 4
По пластине вдоль прямой BD движется точка М; пластина вращается вокруг оси, перпендикулярной плоскости пластины, по известному закону (рис. К-3).
Дано:φ=2t 3 –t 2 (рад); s=AM=18sin(πt/4) см; t1=2/3 с; а=25 см.
Определить:для момента времени t1 абсолютную скорость и абсолютное ускорение.
| Номер рисунка | Для всех рисунков φ=f1(t) | Для рис. К3.0-К3.4 | Для рис. К3.5-К3.9 |
| а, см | S=AM=f2(t) | h | S=AM=f2(t) |
| 4(t 2 -t) | 50(3t-t 2 )-64 | R | (πR/3)·(4t 2 -2t 3 ) |
| 3t 2 -8t | 40(3t 2 -t 4 )-32 | 4R/3 | (πR/2)·(2t 2 -t 3 ) |
| 6t 3 -12t 2 | 80(t 2 -t)+40 | R | (πR/3)·(2t 2 -1) |
| t 2 -2t 3 | 60(t 4 -3t 2 )+56 | R | (πR/3)·(t 4 -3t 2 ) |
| 10t 2 -5t 3 | 80(2t 2 -t 3 )-48 | R | (πR/6)·(3t-t 2 ) |
| 2(t 2 -t) | 60(t 3 -2t 2 ) | R | (πR/3)·(t 3 -2t) |
| 5t-4t 2 | 40(t 2 -3t)+32 | 3R/4 | (πR/2)·(t 3 -2t 2 ) |
| 15t-3t 3 | 60(t-t 3 )+24 | R | (πR/6)·(t-5t 2 ) |
| 2t 3 -11t | 50(t 3 -t)-30 | R | (πR/3)·(3t 2 -t) |
| 6t 2 -3t 3 | 40(t-2t 3 )-40 | 4R/3 | (πR/2)·(t-2t 2 ) |
Решение
1. Анализ задания: точка М совершает сложное движение, так как она движется по пластине вдоль прямой BD и вместе с пластиной, вращающейся вокруг неподвижной оси, перпендикулярной плоскости пластины.
2. Выберем две системы координат: неподвижную с началом координат в точке О1 и подвижную с началом координат в точке М:
— абсолютное движение точки М – её движение относительно неподвижной системы координат O1X1Y1;
— относительное движение точки М – её движение относительно подвижной системы координат ОXY, то есть движение точки по прямой BD; траекторией является прямая;
— переносное движение – движение подвижной системы координат относительно неподвижной, то есть вращение пластины относительно оси, ей перпендикулярной.
3. Положение точки на прямой BD определяется расстоянием s=AM=18sin(πt/4) см, при t1=2/3 с, s=AM= 9 см.
4. Абсолютную скорость точки М найдем как геометрическую сумму относительной и переносной скоростей: 
5. Относительная скорость точки М равна 
6. Определим переносную скорость точки М, мысленно остановив движение точки по прямой BD. В переносном движении точка М описывает окружность радиуса R= ОМ:


Вектор переносной скорости направлен по касательной к окружности в сторону вращения пластины.
7. Найдем модуль абсолютной скорости по формуле: 
8. Абсолютное ускорение точки равно геометрической сумме относительного, переносного ускорений и ускорения Кориолиса:


9. Для определения относительного ускорения точки М мысленно остановим подвижную систему координат и вычислим относительное касательное ускорение: 
Знак «минус» показывает, что вектор относительного касательного ускорения направлен в сторону отрицательных значений S: движение замедленное.
Относительное нормальное ускорение равно нулю, поскольку движение точки М вдоль BD – прямолинейное.
10. Переносное касательное ускорение определяем, мысленно остановив точку М в подвижной системе координат:
Знаки угловой скорости и углового ускорения переносного вращения одинаковы, и, следовательно, движение является ускоренным, направления векторов угловой скорости и углового ускорения совпадают. Векторы касательного ускорения и скорости в переносном движении направлены в одну сторону. Вектор нормального ускорения переносного вращательного движения направлен по радиусу к центру окружности, которую описывает тот
пункт подвижной системы координат, с которым совпадает точка М в данный момент времени.
11. Определяем модуль ускорения Кориолиса: 
12. Модуль абсолютного ускорения точки М найдем, предварительно спроецировав обе части векторного равенства, представленного выше, на координатные оси:
Ответ:V=58,29 см/c, a=316,13 см/c 2 .
ЛИТЕРАТУРА
1. Яблонский А.А., В.М.Никифорова Курс теоретической механики. Учеб.пособие для вузов: 13-е изд., исправ.-М.: Интеграл-Пресс,2006.-603с.
2. Л.А. Голдобина. Теоретическая механика: Задания и методические указания к выполнению контрольной работы для студентов заочной формы обучения. Санкт – Петербург: СПбГУСЭ,2007.
3. Тарг С.М. Краткий курс теоретической механики: Учеб. для втузов/С.М.Тарг.-15-е изд.,стер.-М.:Высш.шк.,2005.-415 с.
4. Бутенин Н.В. и др. Курс теоретической механики: Учеб.пособие для студов вузов по техн.спец.:В 2-х т./Н.В.Бутенин, Я.Л.Лунц, Д.Р.Меркин. СПб.: Лань.-5-е изд., испр.-1998.-729 с.
5. Мещерский И.В. Задачи по теоретической механике: Учеб. пособие для студ.вузов,обуч.по техн.спец./И.В.Мещерский; Под ред. В.А.Пальмова, Д.Д.Меркина.-45-е изд.,стер.-СПб.и др.: Лань,2006.-447 с. 2. Тарг С.М. Краткий курс теоретической механики: Учеб. для втузов/С.М.Тарг.-15-е изд.,стер.-М.:Высш.шк.,2005.-415 с.
6. Сборник заданий для курсовых работ по теоретической механике: Учеб. пособие для студ.втузов/[А.А. Яблонский, С. С.Норейко,С.А.Вольфсон и др.];Под общ. ред. А. А. Яблонского.- 11-е изд.,стер.-М.:Интеграл- Пресс,2004.-382 с.
7. Бать М.И и др. Теоретическая механика в примерах и задачах. Учеб.пособ. для вузов. В 2-х т./М.И.Бать, Г.Ю.Джанелидзе, А.С. Кельзон.-9-е изд., перераб.-М.:Наука,1990.-670 с.
8. Теоретическая механика. Терминология. Буквенные обозначения величин: Сборник рекомендуемых терминов. Вып. 102. М.: Наука, 1984. – 48с.
Приложение А.1. Пример оформления титульного листа курсовой работы
💡 Видео
Урок 90. Движение по окружности (ч.2)Скачать

Урок 89. Движение по окружности (ч.1)Скачать

Урок 102. Метод мгновенных осейСкачать

Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Мгновенная ось вращения. Лекция 2-2Скачать

Урок 88 (осн). Линейная скорость точки на вращающемся телеСкачать

Лекция №8 "Специальная теория относительности. Вращение тела вокруг неподвижной оси" (Булыгин В.С.)Скачать

Физика | Равномерное движение по окружностиСкачать

Формулы механики 2, движение по окружности, центростремительное ускорениеСкачать

Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

§2.2. Вращение твердого тела вокруг неподвижной оси.Скачать

Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Урок 95. Теорема о взаимно перпендикулярных осяхСкачать

Вращение твердого тела вокруг неподвижной оси. Момент инерции. Примеры. Лекция 7-1Скачать

Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать

№535. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 60Скачать