 Линейная функция Линейная функция |
 График линейной функции График линейной функции |
 Прямые, параллельные оси ординат Прямые, параллельные оси ординат |
 Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые |
- Линейная функция
- График линейной функции
- Прямые, параллельные оси ординат
- Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
- Построение параллельных прямых
- Построение параллельных прямых с помощью циркуля и линейки
- Готовые работы на аналогичную тему
- Построение параллельных прямых с помощью угольника и линейки
- Построение параллельной прямой, отстоящей на заданное расстояние от данной прямой
- Другие способы построения параллельных прямых
- Построение параллельных прямых
- Изображение параллельных прямых с применением угольника и линейки
- Изображение параллельных прямых с использованием циркуля и линейки
- Изображение параллельной прямой, отдаленной на определенное расстояние от имеющейся
- Прочие способы изображения параллельных прямых
- Не нашли нужную информацию?
- Гарантия возврата денег
- Отзывы студентов о нашей работе
- 💡 Видео
Видео:6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Линейная функция
Линейной функцией называют функцию, заданную формулой
| y = kx + b, | (1) |
где k и b – произвольные (вещественные) числа.
При любых значениях k и b графиком линейной функции является прямая линия .
Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .
Видео:Параллельные прямые. 6 класс.Скачать

График линейной функции
При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.
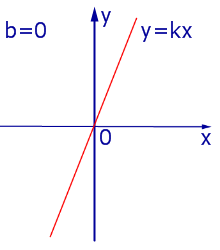 |
| Рис.1 |
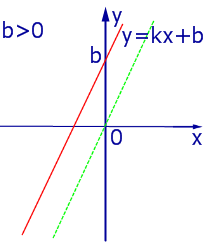 |
| Рис.2 |
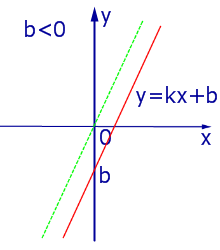 |
| Рис.3 |
При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.
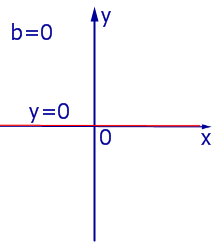 |
| Рис.4 |
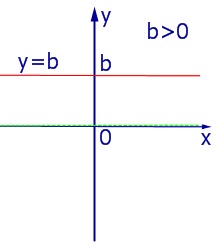 |
| Рис.5 |
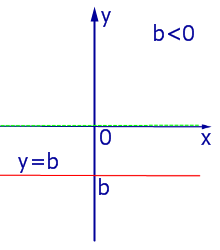 |
| Рис.6 |
При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.
| k y = kx + b1 и y = kx + b2 , имеющие одинаковые угловые коэффициенты и разные свободные члены имеющие разные угловые коэффициенты y = kx + b1 и перпендикулярны при любых значениях свободных членов. Угловой коэффициент прямой линии
равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).
Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b . При Видео:Параллельные прямые | Математика | TutorOnlineСкачать  Прямые, параллельные оси ординатПрямые, параллельные оси Oy , задаются формулой
где c – произвольное число, и изображены на рис. 13, 14, 15.
Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .; Видео:6 класс, Мерзляк, К.р.11, В-1.Перпендикулярные и параллельные прямые.Координатная плоскость. ГрафикиСкачать  Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
где p, q, r – произвольные числа. В случае, когда что и требовалось. В случае, когда откуда вытекает, что уравнение (4) задает прямую линию вида (3). В случае, когда q = 0, p = 0, уравнение (4) имеет вид
и при r = 0 его решением являются точки всей плоскости: В случае, когда Замечание 2 . При любом значении r1 , не совпадающем с r прямая линия, заданная уравнением
параллельна прямой, заданной уравнением (4) . Замечание 3 . При любом значении r2 прямая линия, заданная уравнением
перпендикулярна прямой, заданной уравнением (4) . Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и
В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде
где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство Итак, уравнение прямой, параллельной к прямой В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде
где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство Видео:ПЕРПЕНДИКУЛЯРНЫЕ и ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. КООРДИНАТНАЯ ПЛОСКОСТЬ. Контрольная №11. 6 классСкачать  Построение параллельных прямыхВы будете перенаправлены на Автор24 В основе способов построения параллельных прямых с помощью различных инструментов лежат признаки параллельности прямых. Видео:Перпендикулярные прямые. 6 класс.Скачать  Построение параллельных прямых с помощью циркуля и линейкиРассмотрим принцип построения параллельной прямой, проходящей через заданную точку, с помощью циркуля и линейки. Пусть дана прямая и некоторая точка А, которая не принадлежит данной прямой. Необходимо построить прямую, проходящую через заданную точку $А$ параллельно данной прямой. На практике зачастую требуется построить две или более параллельных прямых без данной прямой и точки. В таком случае необходимо начертить прямую произвольно и отметить любую точку, которая не будет лежать на данной прямой. Рассмотрим этапы построения параллельной прямой:
На пересечении окружности и прямой отметим точку и назовем ее $С$. С тем же радиусом $АВ$ построим окружность с центром в точке $С$. Обратим внимание, что вторая построенная окружность обязательно должна пройти через точку В при правильном выполнении построения. С прежним радиусом $АВ$ построим третью окружность с центром в точке $А$. Отметим точку пересечения второй и третьей построенных окружностей и назовем ее $D$. Отметим, что третья окружность при правильном построении также должна пройти через точку $В$. Через точки $А$ и $D$ проведем прямую, которая будет параллельной заданной. Таким образом, получили параллельные прямые $ВС$ и $АD$: $BC parallel AD$, т. $A in AD$. На практике также применяют метод построения параллельных прямых с помощью чертежного угольника и линейки. Готовые работы на аналогичную темуВидео:Параллельные прямые циркулемСкачать  Построение параллельных прямых с помощью угольника и линейкиДля построения прямой, которая будет проходить через точку М параллельно данной прямой а, необходимо:
Мы получили прямую, проходящую через заданную точку $М$, параллельную данной прямой $а$: $a parallel b$, т. $M in b$. Параллельность прямых $а$ и $b$ видна из равности соответственных углов, которые отмечены на рисунке буквами $alpha$ и $beta$. Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать  Построение параллельной прямой, отстоящей на заданное расстояние от данной прямойВ случае необходимости построения прямой, параллельной заданной прямой и отстоящей от нее на заданном расстоянии можно воспользоваться линейкой и угольником. Пусть дана прямая $MN$ и расстояние $а$.
Если отложить на прямой $АВ$ от точки $В$ отрезок $ВС=а$ в другую сторону, то получим еще одну параллельную прямую к заданной, отстоящую от нее на заданное расстояние $а$. Видео:Построение параллельной плоскости на расстояние 30 мм.Скачать  Другие способы построения параллельных прямыхЕще одним способом построения параллельных прямых является построение с помощью рейсшины. Чаще всего данный способ используют в чертежной практике. При выполнении столярных работ для разметки и построения параллельных прямых, используется специальный чертежный инструмент – малка – две деревянные планки, которые скрепляются шарниром. Получи деньги за свои студенческие работы Курсовые, рефераты или другие работы Автор этой статьи Дата последнего обновления статьи: 22 07 2021 Видео:Построение прямой, параллельной даннойСкачать  Построение параллельных прямыхДля изображения в пространстве прямых, что параллельны друг другу, с использованием разнообразных инструментов опираются на свойства их параллельности. Видео:Перпендикулярные и параллельные прямые. Математика 6 классСкачать  Изображение параллельных прямых с применением угольника и линейкиИспользуем принцип изображения параллельной прямой, что пересекает заданную точку, с использованием чертежного угольника и линейки. Рассмотрим порядок действий при этом способе построения. Допустим, изображены прямая a и точка (M) , не лежащая на ней:
Видео:Видеоурок "Координатная плоскость, координата точки"Скачать  Изображение параллельных прямых с использованием циркуля и линейкиТакже широко применяется способ изображения параллельных прямых с применением линейки и циркуля. Допустим есть прямая и точка (A) , не лежащая на ней. Необходимо изобразить прямую, параллельную существующей прямой и пересекающую заданную точку (A) . Часто требуется просто изобразить параллельные прямые без начальных условий. В подобном варианте просто нужно самостоятельно изобразить прямую и поставить точку, не лежащую на этой прямой. Не нашли что искали? Просто напиши и мы поможем Итак, порядок изображения параллельной прямой:
В итоге мы имеем две прямые (BC) и (AD) , параллельные между собой. Видео:9 класс, 7 урок, Уравнение прямойСкачать  Изображение параллельной прямой, отдаленной на определенное расстояние от имеющейсяДля изображения параллельной прямой, относительно имеющейся, на определенном конкретном расстоянии можно использовать угольник и линейку. (К) примеру, изображена прямая (MN) и задано некое расстояние (a) :
Возможно также на прямой (AB) отмерить расстояние (a) от точки (B) в противоположную сторону, проделать все вышеописанное и начертить еще одну прямую параллельно существующей прямой (MN) . Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать  Видео:Построение параллельных прямыхСкачать  Прочие способы изображения параллельных прямыхВ чертежной сфере часто применяют способ изображения с использованием рейсшины. Столяры при изготовлении изделий часто используют так называемый инструмент – малку, состоящую из двух планок на шарнирах. Этим инструментом наносят разметку с использованием принципов параллельных прямых. Не нашли нужную информацию?Закажите подходящий материал на нашем сервисе. Разместите задание – система его автоматически разошлет в течение 59 секунд. Выберите подходящего эксперта, и он избавит вас от хлопот с учёбой. Гарантия низких цен Все работы выполняются без посредников, поэтому цены вас приятно удивят. Доработки и консультации включены в стоимость В рамках задания они бесплатны и выполняются в оговоренные сроки. Вернем деньги за невыполненное задание Если эксперт не справился – гарантируем 100% возврат средств. Тех.поддержка 7 дней в неделю Наши менеджеры работают в выходные и праздники, чтобы оперативно отвечать на ваши вопросы. Тысячи проверенных экспертов Мы отбираем только надёжных исполнителей – профессионалов в своей области. Все они имеют высшее образование с оценками в дипломе «хорошо» и «отлично». Гарантия возврата денегЭксперт получил деньги, а работу не выполнил? Деньги хранятся на вашем балансе во время работы над заданием и гарантийного срока Гарантия возврата денег В случае, если что-то пойдет не так, мы гарантируем возврат полной уплаченой суммы Видео:2. Построения с помощью циркуля и линейки.Скачать  Отзывы студентов о нашей работе
«Всё сдал!» — безопасный онлайн-сервис с проверенными экспертами Используя «Всё сдал!», вы принимаете пользовательское соглашение Принимаем к оплате 💡 ВидеоПрямоугольная система координат. Координатная плоскость. 6 класс.Скачать  7 класс, 7 урок, Координатная плоскостьСкачать  Урок ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕСкачать  Перпендикулярные и параллельные прямые. Координатная плоскость.Скачать  |

 , параллельны .
, параллельны . , пересекаются при любых значениях свободных членов.
, пересекаются при любых значениях свободных членов.



 прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле
прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле



 уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .
уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .

 получаем:
получаем:

 уравнение (5) решений вообще не имеет.
уравнение (5) решений вообще не имеет.














