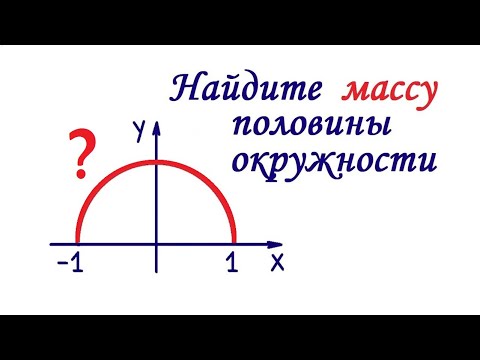Если дан криволинейный интеграл, а кривая, по которой происходит интегрирование — замкнутая (называется контуром), то такой интеграл называется интегралом по замкнутому контуру и обозначается следующим образом:
.
Область, ограниченную контуром L обозначим D. Если функции P(x, y) , Q(x, y) и их частные производные 
и 
— функции, непрерывные в области D, то для вычисления криволинейного интеграла можно воспользоваться формулой Грина:
.
Таким образом, вычисление криволинейного интеграла по замкнутому контуру сводится к вычислению двойного интеграла по области D.
Формула Грина остаётся справедливой для всякой замкнутой области, которую можно проведением дополнительных линий на конечное число простых замкнутых областей.
Пример 1. Вычислить криволинейный интеграл
,
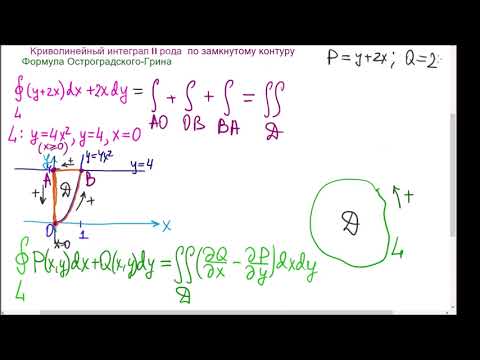
если L — контур треугольника OAB , где О(0; 0) , A(1; 2) и B(1; 0) . Направление обхода контура — против часовой стрелки. Задачу решить двумя способами: а) вычислить криволинейные интегралы по каждой стороне треугольника и сложить результаты; б) по формуле Грина.
а) Вычислим криволинейные интегралы по каждой стороне треугольника. Сторона OB находится на оси Ox , поэтому её уравнением будет y = 0 . Поэтому dy = 0 и можем вычислить криволинейный интеграл по стороне OB :
Уравнением стороны BA будет x = 1 . Поэтому dx = 0 . Вычисляем криволинейный интеграл по стороне BA :
Уравнение стороны AO составим, пользуясь формулой уравнения прямой, проходящей через две точки:
.
Таким образом, dy = 2dx . Вычисляем криволинейный интеграл по стороне AO :
Данный криволинейный интеграл будет равен сумме интегралов по краям треугольника:
.
б) Применим формулу Грина. Так как 
, 
, то 
. У нас есть всё для того, чтобы вычислить данный интеграл по замкнутому контуру по формуле Грина:
Как видим, получили один и тот же результат, но по формуле Грина вычисление интеграла по замкнутому контуру происходит значительно быстрее.
Пример 2. Пользуясь формулой Грина, вычислить криволинейный интеграл
,
где L — контур OAB , OB — дуга параболы y = x² , от точки О(0; 0) до точки A(1; 1) , AB и BO — отрезки прямых, B(0; 1) .
Решение. Так как функции 
, 
, а их частные производные 
, 
, D — область, ограниченная контуром L , у нас есть всё, чтобы воспользоваться формулой Грина и вычислить данный интеграл по замкнутому контуру:
Пример 3. Пользуясь формулой Грина, вычислить криволинейный интеграл
, если L — контур, который образуют линия y = 2 − |x| и ось Oy .
Решение. Линия y = 2 − |x| состоит из двух лучей: y = 2 − x , если x ≥ 0 и y = 2 + x , если x .
Имеем функции 
, 
и их частные производные 
и 
. Подставляем всё в формулу Грина и получаем результат:
Пример 4. С помощью формулы Грина вычислить криволинейный интеграл
,
если L — окружность 
.
Решение. Функции 
, 
и их частные производные 
и 
непрерывны в замкнутом круге . Подставляем всё в формулу Грина и вычисляем данный интеграл:
Видео:Формула ГринаСкачать
Примеры решений криволинейных интегралов
В этом разделе вы найдете подробные решения криволинейных интегралов первого и второго рода (непосредственное вычисление, по разным путям, по формуле Грина), а также применение к вычислению моментов инерции, массы, работы, силы притяжения и т.п.
Видео:Математический анализ, 47 урок, Криволинейные интегралы первого родаСкачать
Криволинейные интегралы 1-го рода: примеры решений
Задача 1. Вычислить криволинейный интеграл первого рода по указанной кривой $L$:
Задача 2. Вычислить криволинейный интеграл I рода $int_L y^2 dl$, $L$ — арка циклоиды $x=(t-sin t)/2$, $y=(1-cos t)/2$, $0 le t le pi$.
Задача 3. Вычислить криволинейный интеграл $int_L y^2 dl$, где $L$ – дуга параболы $y^2=2x$ от точки $(0;0)$ до точки $(1;sqrt)$.
Если вам нужна помощь в нахождении интегралов, выполнении домашней работы, будем рады принять ваш заказ на решение. Стоимость от 100 рублей, срок от нескольких часов.
Видео:Интеграл по замкнутому контуру.Без формулы ГринаСкачать
Криволинейные интегралы 2-го рода: примеры решений
Задача 4. Вычислить криволинейный интеграл второго рода, взятый вдоль ориентированной кривой $L$: $int_L x^2 dy -xydx$, где $L$ — часть кривой $x^4-y^4=6x^2y$ от точки $A=(-4sqrt;4)$ до точки $B=(0;0)$
Задача 5. Вычислить интеграл $$int_L z^2x dx +(z+x+y)dy +y^2zdz,$$ где $L$ — кривая $a^2+y^2=ax, x^+y^2=z^2$ положительно ориентированная на внешней стороне цилиндра.
Задача 6. Вычислить криволинейный интеграл $int_ (y^2+x)dx+2x/y dy$ вдоль кривой $y=e^x$ от точки $A(0;1)$ до точки $B(1;e)$.
Задача 7. Проверить, что криволинейный интеграл не зависит от пути интегрирования и найти его значение.
Задача 8. Проверить криволинейный интеграл, который не зависит от пути интегрирования, и найти его значение (двумя способами – непосредственно и с помощью потенциала).
Задача 9. Вычислить криволинейный интеграл по замкнутому контуру в положительном направлении, используя формулу Грина
$$int_l (x-y^2)dy + (x^3+3y)dx, quad l: x=y, y=x^2.$$
Трудности с задачами? МатБюро поможет с интегралами.
Видео:Криволинейный интеграл 1-го рода ★ Криволинейный интеграл по длине дуги ★ ∫(x+y)dsСкачать
Моменты инерции: примеры решений
Задача 10. Найти моменты инерции относительно осей однородных дуг $L$ плотности $rho$.
Задача 11. Вычислить момент инерции верхней половины окружности $x^2+y^2=a^2$ относительно оси $Oy$, если плотность $delta=1$.
Видео:Формула Остроградского - ГринаСкачать
Другие задания: примеры решений
Задача 12. Найти координаты силы притяжения дугой астроиды $x=a cos^3 t$, $y=a sin^3 t$, $0 le t le pi/2$ единичной массы, помещенной в начале координат, если плотность астроиды в каждой ее точке равна кубу расстояния этой точки от начала координат.
Задача 13. Вычислить работу силы $F(z,-x,y)$ вдоль дуги винтовой линии $z=2cos t$, $y=3sin t$, $z=4t$, $0 le t le 2pi$.
Задача 14. Доказать, что данное выражение $P(x,y)dx+Q(x,y)dy$ является полным дифференциалом функции $Ф(x,y)$ и найти ее с помощью криволинейного интеграла.
Задача 15. Вычислить работу силы $overline$ при перемещении точки приложения силы вдоль заданной кривой $L$ от точки $B$ до точки $C$, если значения параметра $t$ в точках $B$ и $C$ заданы.
$$ overline=-x overline+2y^2overline, quad x=2cos t, y=sint, quad t_B=0, t_C=pi/6. $$
Задача 16. Вычислить массу кривой $y=x^2/2$, где $xin (sqrt, 2sqrt)$, если линейная плотность задана функцией $f(x,y)=6y/x$.
Видео:Криволинейный интеграл 1 родаСкачать
Криволинейный интеграл по замкнутому контуру окружности
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
 |
