Диаметр делительной окружности косозубого цилиндрического колеса (2 видео)

Диаметр делительной окружности косозубого цилиндрического колеса

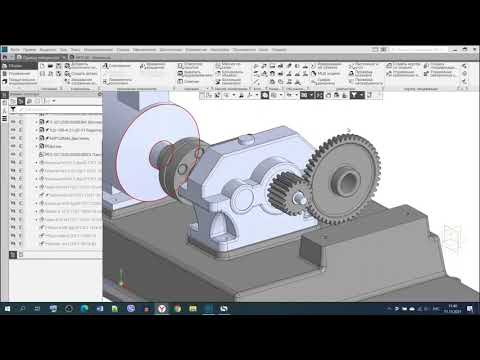
Классификация передач. По форме различают цилиндрические, конические, реечные, эллиптические, фигурные зубчатые колеса и с неполным числом зубьев. В зависимости от взаимного расположения; зубчатых колес различают зубчатые передачи с внешним и внутренним зацеплением, а также разделяются на открытые и закрытые (рис. 81).

Назначение. Зубчатые передачи относятся к механическим передачам зацепления с непосредственным контактом и применяются для изменения скорости или направления вращения ведомого звена с соответствующим изменением крутящего момента, получения точных перемещений, при необходимости точного соответствия скоростей и положений ведущего и ведомого звеньев в произвольный момент времени. Зубчатая передача состоит из двух колес с зубьями, посредством которых они сцепляются между собой. Вращение ведущего зубчатого колеса преобразуется во вращение ведомого колеса путем нажатия зубьев первого на зубья второго. Меньшее зубчатое колесо передачи называется шестерней, большее — колесом. Зубчатые передачи могут преобразовывать вращательное движение между валами с параллельными, пересекающимися и перекрещивающимися осями.

Рис. 81. Виды зубчатых передач: а – внешнего зацепления прямозубая, б – внешнего зацепления косозубая, в – внутреннего зацепления прямозубая, г – внешнего зацепления реечная, д – внешнего зацепления шевронная, е – коническая прямозубая, ж – коническая косозубая, з – коническая круговая, и – коническая круговая — гипоидная, к – внешнего зацепления винтовая, л – передача с круговыми зубьями, м — планетарная.

Преимущества. Важнейшие: компактность, высокий КПД, постоянство передаточного числа, большая долговечность и надежность в работе, возможность осуществления передачи практически любых мощностей при практически любых скоростях и передаточных отношениях, простота обслуживания. Высокая технологичность, которая обусловлена высокопроизводительным специальным оборудованием и технологиями.

Недостатки. Высокие требования к качеству изготовления и монтажа. Шум при больших скоростях. Концентрация напряжений в эвольвентных передачах при точечном контакте и чувствительность к ошибкам монтажа в передачах с линейным контактом. Поэтому для реализации преимуществ при изготовлении деталей необходимо применять высококачественные материалы и технологии изготовления.

Сферы применения. 3убчатые передачи нашли самое широкое распространение среди механических передач в машинах различных отраслей. Назначение и конструкции зубчатых передач разнообразны. Их применяют во многих приборах и почти во всех машинах, в том числе и самых тяжелых и мощных для передачи мощностей до 65 тыс.кВТ (65МВт), с диаметром колес от долей миллиметра до 6м и более. Окружная скорость зубьев может достигать 270м/с. Передаточные отношения для открытой передачи принимают 10, а для закрытой 25. КПД одной ступени зубчатой передачи при высоком качестве изготовления и монтажа может достигать 0,99.

Геометрический расчет. Передаточное отношение передачи

, (14.1)

где — число зубьев шестерни и колеса соответственно.

Номинальные значения передаточных чисел и зубчатых редукторов общего назначения, выполненных в виде самостоятельных агрегатов стандартизированы:

1-й ряд 1,00; 1,25; 1,60; 2,00; 2,50; 3,15; 4,0; 5,0; 6,3; 8,0; 10,0;12,5.

2-й рад 1,12; 1,40; 1,80; 2,24; 2,80; 3,55; 4,5; 5,6; 7,1; 9,0; 11,2.

При выборе стандартных параметров первый ряд предпочтительнее второго, а принятые значения передаточных чисел не должны отличаться от расчетных не более чем на 3%.

Расстояние между осями зубчатых колес цилиндрической передачи по межосевой линии называется межосевым расстоянием:

, (14.2)

где и — начальные диаметры шестерни и колеса; знак плюс относится к передаче с внешним зацеплением, а минус — к передаче с внутренним зацеплением.

Стандартизированы номинальные значения межосевых расстояний aw, мм:

1-й ряд 40; 50; 63; 80100; 125; 160; 200; 250; 315; 400; 500; 630; 800

2-й ряд — — 71; 98; 112; 140; 180; 225; 280; 355; 450; 560; 710; 900.

Межосевое расстояние цилиндрической зубчатой передачи, равное полусумме делительных диаметров колеса d2 и шестерни при внешнем зацеплении или полуразности при внутреннем зацеплении, называется делительным межосевым расстоянием:

. (14.3)

Делительные диаметры для зубчатых колес прямозубой передачи

для косозубой и шевронной

. (14.5)

где т — модуль зацепления основная характеристика размеров зубчатых и червячных колес. Для обеспечения взаимозаменяемости и унификации инструмента для изготовления модули цилиндрические и конические эвольвентных зубчатых колес стандартизованы: для цилиндрических колес — значения нормальных модулей, для конических — значения окружных делительных модулей в диапазоне 0,05..100мм.

1-й ряд 1,0; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25;

2-й ряд 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14; 18; 22; 28.

Ширина венца цилиндрического зубчатого колеса определяется по одной из формул

, (14.6)

, (14.7)

где — коэффициент ширины зубчатого венца по межосевому расстоянию, а — коэффициент ширины зубчатого венца по диаметру шестерни.

Коэффициенты и связаны зависимостью:

. (14.8)

Значения коэффициентов ширины венца зубчатых колес по межосевому расстоянию выбираются из стандартного ряда: 0,1; 0,125; 0,16; 0,2; 0,250; 0,315; 0,400; 0,500; 0,630; 0,800; 1,000; 1,25 и т. д.

Рис. 82. Обозначения элементов зубчатого зацепления.

Для заданного числа зубьев и , коэффициентов смещения исходного контура и , угла наклона зубьев основные параметры эвольвентных цилиндрических колес внешнего зацепления, показанные на рис 82 в соответствии с ГОСТ 13755-81 определяются по расчетным формулам:

Параметр

Шестерня

Колесо

Диаметр вершин зубьев

Диаметр впадин зубьев

Делительный угол профиля в торцевом сечении

Коэффициент торцевого перекрытия

Рабочая ширина зубчатого венца

Коэффициент осевого перекрытия (при ширине венца )

Основной угол наклона

Кинематический и силовой расчет. Расчетная окружная скорость v цилиндрической передачи:

— шестерни ; (14.9)

— колеса ,

где — угловая скорость зубчатого колеса; п — частота вращения зубчатого колеса; — начальный диаметр цилиндрического зубчатого колеса.

Окружная сила цилиндрической зубчатой передачи Ft

, (14.10)

где — крутящий момент на шестерне.

Сила давления между зубьями в цилиндрической прямозубой передаче

. (14.11)

Составляющие этой силы: в цилиндрических прямозубых (рис. 83) и шевронных передачах — окружная сила , и радиальная сила , в конической прямозубой и цилиндрической косозубой передачах — окружная сила , радиальная сила , и осевая сила Fa.

Радиальная сила в цилиндрической передаче

, (14.12)

Осевая сила, действующая на колесо косозубой цилиндрической передачи

, (14.13)

Критерии работоспособности зубчатых передач. Учитывая виды повреждений критериями работоспособности зубчатых передач являются контактная и изгибная прочность зубьев. Проектный расчет закрытых передач малой и средней твердости выполняется на контактную выносливость. Расчет на изгибную прочность зубьев в этом случае выполняется как проверочный. Для зубчатых колес высокой прочности () размеры передачи определяются из расчета зубьев на изгиб, а проверочный расчет выполняется по контактным напряжениям. Для открытой передачи проектный расчет выполняется из условия предупреждения поломки зуба с учетом износа зубьев, проверочный расчет выполняется из условия обеспечения контактной прочности.

Проектные расчеты зубчатых передач.

Расчет зубьев на контактную прочность выполняют для зацепления в полюсе, так как выкрашивание зубьев начинается у полюсной линии. По зависимости для проектного расчета на контактную прочность зубьев определяется межосевое расстояние

, (14.14)

где — коэффициент для прямозубых передач Ка = 495, а для косозубых Ка= 430, — момент на зубчатом колесе передачи в , — коэффициент неравномерности распределения нагрузки по длине контактных линий в результате погрешностей в зацеплении и деформации зубьев, который определяется по рис. 84; — допускаемое контактное напряжение в МПа.

Рис.84. Коэффициенты неравномерности распределения нагрузки по длине контактных линий для расчета на контактную прочность.

Коэффициент ширины венца по межосевому расстоянию для редукторов принимают равным: для зубчатых колес из улучшенных сталей при несимметричном расположении = 0,315. 0,4; для зубчатых колес из закаленных сталей = 0,25. 0,315; при симметричном расположении зубчатых колес относительно опор = 0,4. 0,5; для передвижных зубчатых колес коробок скоростей = 0,1. 0,2. Принимаются стандартные значения .

Допускаемое контактное напряжение

, (14.15)

где — предел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов напряжений (табл. 14.1); — коэффициент безопасности; ZR — коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев; Zv — коэффициент, учитывающий окружную скорость передачи; KHL — коэффициент долговечности. Коэффициент безопасности зубчатых колес с однородной структурой материала sH = 1,1; с поверхностным упрочением зубьев sH = 1,2. Коэффициент ZR = 0,9. 1; ZR =1,0 при мкм, ZR =0,95 при мкм и ZR =0,9 при мкм. Коэффициент Zv = 1. 1.16; чем меньше скорость передачи и тверже зубья, тем меньше Zv. При v 350).

При известном межосевом расстоянии ориентировочное значение модуля передачи определяется по зависимости

, (14.27)

где — коэффициент для прямозубой передачи =1400, для косозубой и шевронной =850.

Значение модуля зацепления полученное по формуле (14.27) округляется до ближайшего стандартного значения. После определения значений межосевого расстояния и модуля определяются число зубьев и все геометрические параметры передачи по которым выполняется проверочные расчеты.

Проверочные расчеты зубчатых передач.

Расчет зубьев на контактную прочность выполняется по известным геометрическим параметрам передачи при выбранной степени точности изготовления зубьев колес по зависимости

— для прямозубых передач

; (14.28)

— для косозубых передач

, (14.29)

где , — коэффициент неравномерности распределения нагрузки между зубьями в зависимости от скорости и точности изготовления; — коэффициент динамической нагрузки, возникающей в зацеплении.

Таблица 14.3 Значения коэффициента динамических нагрузок

Степень точности

Твердость поверхностей зубьев

υ, м/с

Диаметр делительной окружности косозубого цилиндрического колеса

Примечания: 1. Твердость поверхности зубьев: а) и или и ; б) и . 2. 3начения в числителе относятся к прямозубым передачам, а в знаменателе — к косозубым.

Рис. 87.Коэффициенты неравномерности распределения нагрузки между зубьями : а — для расчета на контактную прочность, b – для расчета на изгибную прочность.

Коэффициент неравномерности распределения нагрузки для прямозубых передач принят КНа = 1, а для косозубых коэффициент определяются по графикам на рис.87. Коэффициент динамической нагрузки определяют по таблице 14.3.

При действии на зубья кратковременных перегрузок выполняется проверка рабочих поверхностей зубьев на контактную прочность по максимальному контактному напряжению:

, (14.30)

где — максимальное расчетное напряжение при перегрузке зубьев максимальным моментом ; — допускаемое максимальное контактное напряжение для зубьев; — расчетное контактное напряжение, вызываемое расчетным моментом и определяемое по формуле (14.27) или (14.28). Для зубьев зубчатых колес и термообработкой нормализацией, улучшением или объемной закалкой с отпуском , где — предел текучести материала зубьев при растяжении; для зубьев с термообработкой — цементация, контурная закалка после нагрева ТВЧ — ; для азотированных зубьев . Расчет зубьев по формуле (14.30) производится раздельно для колеса и для шестерни.

Расчет зубьев на изгибную прочность выполняется по известным геометрическим параметрам передачи при выбранной степени точности изготовления зубьев колес по зависимости

, (14.31)

где — коэффициент учитывающий перекрытие зубьев; — коэффициент наклона зубьев; — коэффициент распределения нагрузки между зубьями; — коэффициент динамической нагрузки, возникающей в зацеплении при работе передачи, — коэффициент ширины венца зубчатого колеса по начальному диаметру шестерни.

При подстановке окружной силы по зависимости (14.10) формула (14.31) преобразуется к виду

Коэффициент, учитывающий перекрытие зубьев

При приближенных расчетах для для косозубых передач и прямозубых передач принимают .

Коэффициент наклона зубьев для прямозубых передач , для косозубых определяется по зависимости

, (14.32)

при .

Коэффициент неравномерности распределения нагрузки для прямозубых передач принят , а для косозубых коэффициент определяются по графикам на рис.87. Коэффициент динамической нагрузки определяют по таблице 14.4

Таблица 14.4 Значения коэффициента динамических нагрузок

Степень точности

Твердость поверхностей зубьев

Содержание

Модуль зубьев зубчатого колеса: расчет, стандартные, определение
Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки
Зубчатые передачи
Типы зубчатых передач
Эвольвентное зацепление
Форма зубьев
Рис. Характеристики прямозубой цилиндрической передачи передачи (циклоидное зацепление)
Коррегирование зубчатого зацепления
Зубчатые передачи с точно заданным межосевым расстоянием
Зубчатые передачи с изменяемым межосевым расстоянием
Расчетные формулы для зубчатых передач
Степени точности зубчатых передач (DIN 3961…..3964)
Зубчатые передачи стартера
Модули зубчатых передач стартеров
Стандарты зубчатых передач США
Полная высота зуба
Ножка зуба
Система обозначений и преобразований
Расчет наибольшего допустимого давления зубчатых передач
Величины и единицы измерения для расчета наибольшего допустимого давления
Коэффициент срока службы ф
Расчет зубчатого зацепления на изгиб и разрушение зуба
Коэффициент профиля зуба YFa
Скоростной фактор fv
Примерный расчет элементов зубчатого колеса
Вычерчивание контура зуба
Определение основных геометрических параметров зубчатых колес
Модуль зуба – Модуль шестерни. Формулы расчёта
Как определить модуль шестерни с прямым и косым зубом
Модуль зубчатого колеса – это… Что такое Модуль зубчатого колеса?
Смотреть что такое “Модуль зубчатого колеса” в других словарях:
Модуль зуба что такое
Модуль зубьев зубчатого колеса
Что такое модуль зубчатого колеса
Что же такое модуль шестерни?
Формула расчета параметров прямозубой передачи
Исходные данные и замеры
Результаты расчетов
Расчет параметров колеса и шестерни косозубой передачи
Расчёт модулей зубчатых колёс
Диаметр делительной окружности косозубого цилиндрического колеса
🌟 Видео

Видео:6.3 Зубчатые цилиндрические передачиСкачать

Модуль зубьев зубчатого колеса: расчет, стандартные, определение

Видео:Модуль шестерни и параметры зубчатого колесаСкачать

Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки

Диаметр делительной окружностиd является одним из основных параметров, по которому производят расчет зубчатого колеса:
d = m × z,
где z – число зубьев;
m – модуль.
Модуль зацепленияm – это часть диаметра делительной окружности, приходящейся на один зуб:
m = t / π,
где t – шаг зацепления.
Высота зуба:
h = ha + hf,
где ha – высота головки зуба, ha = m; hf – высота ножки зуба, hf = 1,25m.
Диаметр окружности выступов зубьев:
da = d + 2ha = m(z + 2).
Диаметр окружности впадин:
df = d – 2hf = m(z – 2,5).
Служит для передачи вращения при параллельных осях валов.
ГОСТ 9563-60 предусматривает два ряда модулей m= 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …

Примечание. Ряд 1 следует предпочитать ряду 2.

Служит для преобразования вращательного движения в возвратно-поступательное.
ГОСТ 9563-60 предусматривает два ряда модулей m= 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …

Примечание. Ряд 1 следует предпочитать ряду 2.

Служит для передачи вращательного движения между валами со скрещивающимися осями.
ГОСТ 19672-74 устанавливает два ряда значений модулей m (мм).
Ряд 1: … 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10 …
Ряд 2: … 1,5; 3; 3,5; 6; 7 …

Примечание. Ряд 1 следует предпочитать ряду 2.

Служит для передачи вращения при пересекающихся осях валов.
ГОСТ 9563-60 предусматривает два ряда модулей m= 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …

Примечание. Ряд 1 следует предпочитать ряду 2.

Видео:Что такое МОДУЛЬ шестерни? Ты ТОЧНО поймешь!Скачать

Зубчатые передачи

Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.

Типы зубчатых передач

Эвольвентное зацепление

Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут изготавливаться на одном оборудовании, независимо от количества зубьев и размеров головки.

Модули зацепления цилиндрических и конических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных передач по DIN 780; модули шлицевых соединений по DIN 5480; модули зубчатого зацепления нормального профиля для шестерен со спиральными зубьями по DIN 780.

Форма зубьев

Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; червячных передач — DIN 3975; шлицевых соединений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).

Форма зубьев гипоидных передач регламентируется стандартом DIN 867. В дополнение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы зацепления 12°, 14°30 15°, 17°30′| 22°30′ и 25°.

Рис. Характеристики прямозубой цилиндрической передачи передачи (циклоидное зацепление)

Коррегирование зубчатого зацепления

Коррегирование зубчатого зацепления (изменение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подрезания у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.

Зубчатые передачи с точно заданным межосевым расстоянием

У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса производится на одинаковую величину, но в противоположных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.

Зубчатые передачи с изменяемым межосевым расстоянием

Изменение высоты головки зуба для шестерни и зубчатого колеса производится независимо друг от друга, поэтому межосевое расстояние передачи может изменяться. Допускаемые отклонения линейных размеров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.

Подставляя jη = 0 в приведенные ниже формулы, рассчитывают параметры зацепления без зазора между зубьями. Для определения зазора между зубьями допускаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в зависимости от требуемой степени точности зубчатой передачи.

Следует отметить, что не обязательно стремиться к нулевому зазору между зубьями. Для компенсации имеющихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес.

Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.

Расчетные формулы для зубчатых передач

Степени точности зубчатых передач (DIN 3961…..3964)

Зубчатые передачи стартера

Система допускаемых отклонений для зубчатых передач по «Стандарту межосевых расстояний» (DIN 3961) применяется в силовых приводах, где требуемый зазор между зубьями обеспечивается отрицательными допусками толщины зубьев. Эта система неприменима для зубчатых передач автомобильных стартеров, поскольку они работают со значительно большими зазорами между зубьями, которые обеспечиваются увеличением межосевого расстояния.

Модули зубчатых передач стартеров

Большой крутящий момент, необходимый для пуска двигателя, требует применения зубчатой передачи с большим передаточным отношением (i = 10-20). Поэтому шестерня стартера имеет малое количество зубьев (z = 9-11), обычно с положительным смещением.

Для шага зубьев принято следующее обозначение: количество зубьев, равное, например, 9/10, означает нарезку девяти зубьев на заготовке, рассчитанной по диаметру на 10 зубьев, и соответствует смещению +0,5. При этом допускаются небольшие отклонения величины коэффициента х.

(Это обозначение нельзя смешивать с обозначением Р 8/10, приведенным ниже).

Стандарты зубчатых передач США

Вместо модуля для стандартизации зубчатых передач в США используется показатель количества зубьев на 1 дюйм (25,4 мм) диаметра делительной окружности или диаметральный модуль (питч) (Р):
Р = z/d = z/(z • m/25,4) =25,4/m
Для перевода стандарта США в европейский стандарт служит зависимость:
m = 25,4 мм / P
Размещение зубьев в пределах диаметрального модуля называется окружным шагом зацепления (CP):
CP = (25,4 мм / P) π.
Табл. Стандарты зубчатых передач

Полная высота зуба

В стандартах США полная высота зуба обозначается как высота головки ha = т, что соответствует величине т в стандартах Германии.

Ножка зуба

Обозначается так же, как и полная высота зуба, но расчет головки зуба основывается на использовании своего модуля. Пример обозначения:
Обозначение (пример): Р 5 /7
Р = 7 для расчета головки зуба,
Р = 5 для расчета других параметров.

Система обозначений и преобразований

Диаметр окружности выступов: OD = da.
Диаметр делительной окружности: PD = N/P = d (в дюймах) или PD = Nm = d (в мм).
Диаметр окружности впадин: RD = df
Начальный диаметр:
LD =(N+2x) / P (в дюймах)
или
LD= (N+2x)·m (в мм).
LD ≈ dw,
где dw — диаметральный модуль.

Расчет наибольшего допустимого давления зубчатых передач

Ниже приведены расчетные формулы, которые могут применяться вместо стандартного расчета DIN 3990 «Расчет несущей способности зубчатых передач». Эти зависимости применимы для расчета нагрузки трансмиссионных зубчатых пар, работающих в стандартном режиме.

Величины и единицы измерения для расчета наибольшего допустимого давления

Необходимое сопротивление усталостному выкрашиванию и изнашиванию металла для шестерни (колесо 1) вследствие высокого контактного давления достигается, если величина оценки сопротивления выкрашиванию Sw равна или больше 1.

В случае зубчатого зацепления с z1 Читайте также: Соленоид 12 вольт своими руками

При оценке сопротивления выкрашиванию металла зубчатых колес Sw расчетный срок их службы может изменяться за счет коэффициента срока службы ф.

Коэффициент допустимого контактного давления kperm в H/mm2 для срока службы Lh = 5000 ч

Прочностные характеристики материалов для изготовления зубчатых передач приведены в табл. «Параметры материалов зубчатых передач«.

При пульсирующей нагрузке для предела усталостной прочности (NL ⩾ 3*106). В случае знакопеременной нагрузки следует применять коэффициент YL
В пределах усталостной прочности в течение срока службы напряжения изгиба увеличиваются на коэффициент Ynt в зависимости от количества циклов нагрузки NL.

Коэффициент срока службы ф

Коэффициент срока службы используется для корректирования приведенных в верхней таблице значений коэффициента допустимого контактного давления kperm (рассчитанного на срок службы Lh = 5000 ч) для различной расчетной продолжительности работы зубчатой передачи.

Рекомендации по выбору расчетного срока службы зубчатых передач: при постоянной работе с полной нагрузкой — от 40 000 до 150 000 ч; при прерывистой полной нагрузке — от 50 до 5000 ч.

Необходимая величина сопротивления разрушению зуба обеспечивается при SF ⩾ 1 для шестерни (колесо 1).

Если шестерня изготовлена из более прочного материала, чем зубчатое колесо 2, следует также произвести проверочный расчет зубчатого колеса на изгибающие нагрузки.

Расчет зубчатого зацепления на изгиб и разрушение зуба

Коэффициент профиля зуба YFa

Скоростной фактор fv

[1] Оценка действительна для А = 6 (средний уровень точности).

В следующей статье я расскажу об электрических свойствах материалов.

Видео:Лекция 5. Червячные передачиСкачать

Примерный расчет элементов зубчатого колеса

Длина всякой окружности равна ΠD; следовательно, длина начальной окружности зубчатого колеса будет выражена формулой Πd,.

Шагом t зацепления называется длина дуги начальной окружности между обращенными в одну сторону (левыми или правыми) профилями двух смежных зубьев см 517, б.

Если размер этой дуги взять столько раз, сколько имеется зубьев у колеса, т. е. z раз, то также получим длину начальной окружности; следовательно,

Отношение шага t зацепления к числу Π называется модулем зацепления, который обозначают буквой m, т. е.

Модуль выражается в миллиметрах. Подставив это обозначение в формулу для d, получим.

Следовательно, модуль можно назвать длиной, приходящейся по диаметру начальной окружности на один зуб колеса. Диаметр выступов равен диаметру начальной окружности плюс две высоты головки зуба (фиг. 517, б) т.е.

Высоту h’ головки зуба принимают равной модулю, т. е. h’ = m. Выразим через модуль правую часть формулы:

De = mz + 2m = m (z + 2) следовательно
m = De : (z +2)

Из фиг. 517,б видно также, что диаметр окружности впадин равен диаметру начальной окружности минус две высоты ножки зуба, т. е.

Di = d — 2h»
Высоту h» ножки зуба для цилиндрических зубчатых колес принимают равной 1,25 модуля: h’ = 1,25m. Выразив через модуль правую часть формулы для Di получим
Di = mz — 2 × 1,25m = mz — 2,5m или
Di = m (z — 2,5m)
Вся высота зуба h = h’ + h» т.е
h = 1m + 1,25m = 2,25m
Следовательно, высота головки зуба относится к высоте ножки зуба как 1 : 1,25 или как 4 : 5.

Толщину зуба s для необработанных литых зубьев принимают приблизительно равной 1,53m, а для обработанных на станках зубьев (например, фрезерованных) — равной приблизительно половине шага t зацепления, т. е. 1,57m.

Зная, что шаг t зацепления равен толщине s зуба плюс ширина sв впадины (t = s + sв) (Величину шага t определяем по формуле t/Π = m или t = Πm ), заключаем, что ширина впадины для колес с литыми необработанными зубьями.

sв = 3,14m — 1,53m = 1,61m A для колес с обработанными зубьями.
sв = 3,14m — 1,57m = 1,57m

Конструктивное оформление остальной части колеса зависит от усилий, которые испытывает колесо во время работы, от формы деталей, соприкасающихся с данным колесом, и др. Подробные расчеты размеров всех элементов зубчатого колеса даются в курсе «Детали машин». Для выполнения графического изображения зубчатых колес можно принять следующие приблизительные соотношения между их элементами:

Толщина обода e = t/2

Диаметр отверстия для вала Dв ≈ 1/в De Диаметр ступицы Dcm = 2Dв Длина зуба (т. е. толщина зубчатого венца колеса) b = (2 ÷ 3) t Толщина диска К = 1/3b Длина ступицы L = 1,5Dв : 2,5Dв

Размеры t1 и b шпоночного паза берутся из таблицы №26. После определения числовых величин модуля зацепления и диаметра отверстия для вала необходимо полученные размеры согласовать с ГОСТ 9563-60 (см таблицу №42) на модули и на нормальные линейные размеры по ГОСТ 6636-60 (таблица №43).

Модули (согласно ГОСТ 9563-60) Таблица №42.

Нормальные линейные размеры. Таблица №43. (Выдержка из ГОСТ 6636-60)

Если они отличаются от табличных значений, надо взять ближайшие большие табличные значения и пересчитать все величины, зависящие от вновь выбранного модуля или диаметра отверстия.

Вычерчивание контура зуба

Видео:Лекция «Цилиндрические зубчатые передачи. Основные параметры»Скачать

Определение основных геометрических параметров зубчатых колес

Лабораторная работа 10
Цель работы — ознакомиться с практическими методами определения основных параметров зубчатых колес.
Краткие теоретические сведения

Основными параметрами зубчатого колеса с эвольвентным профилем зубьев являются: модуль т, число зубьев z, угол зацепления а, величина смещения инструментальной рейки при нарезании зубчатого колеса.

Число зубьев, диаметры окружностей вершин и впадин зубьев можно измерить непосредственно, остальные параметры вычисляют в результате расчета.

Подсчитав число зубьев z, нетрудно определить модуль зацепления, используя свойство эвольвенты: нормаль в любой точке эвольвенты является касательной к основной окружности. Поэтому при охвате нескольких зубьев колеса губками штангенциркуля (размер АВ, рис. 2.5.1) линия АВ будет касательной к основной окружности и нормальной профилям зубьев.

Если отрезок АВ катить по основной окружности, то по свойству эвольвенты точка А придет в точку А0, точка В — в точку В0 и точка D — в точку D0. Тогда

Таким образом, измерив вначале длину общей нормали Wzn (мм), соответствующей числу зубьев z„, а затем размер Wzn+ь охватив губками штангенциркуля на один зуб больше, рь

шаг по основной окружности — определим как разность двух измерений:

Это выражение действительно только в том случае, когда губки штангенциркуля касаются эвольвентной части профиля зуба.

Рис. 2.5.1. Схема замера

Чтобы не возникло кромочного контакта, необходимо правильно выбрать zn (табл. 2.5.1).

Число зубьев колеса	12-18	19-27	28-36	37-45	46-54	55-63	64-72	73-81
2	3	4	5	6	7	8	9

Модуль зацепления определим по формуле

Полученное значение модуля сопоставим со стандартным значением (табл. 2.5.2) и примем его ближайшее значение.

т, мм	2,00	2,25	2,50	2,75	3,00	3,25
Рь, мм	5,904	6,642	7,380	8,818	8,856	9,954
т, мм	3,50	3,75	4,00	4,50	5,00	5,50
Рь, мм	10,33	11,07	11,808	13,28	14,76	16,84

По уточненному значению модуля рассчитаем шаги зацепления по делительной и основной окружностям.

Для определения величины смещения при нарезании зубчатого колеса инструментальной рейкой необходимо измерить толщину зуба по основной окружности, сопоставить результат с расчетным значением той же толщины зуба для колеса, нарезанного без смещения, и найти коэффициент смещения инструментальной рейки:

где sb = Wzn+l — znpb — толщина зуба по основной окружности данного колеса; sb = mcosa(^ + zinva) — толщина зуба по основной окружности зубчатого колеса, нарезанного при х = 0; a = 20°; inv 20° = 0,0149.

При проведении обмера зубчатых колес необходимо измерить также диаметры окружностей выступов da и впадин df.

Если число зубьев шестерни z четное, то оба диаметра могут быть непосредственно измерены штангенциркулем (рис. 2.5.2, а) При нечетном числе зубьев измерение проводится по схеме, изображенной на рис. 2.5.2, б.

Рис. 2.5.2. Определение диаметров при четном (а) и нечетном (б) числе зубьев

Для определения диаметра окружности выступов измеряется диаметр отверстия шестерни ((/0Тв) и размер//’. Тогда диаметр окружности выступов

Аналогично измеряется диаметр окружности впадин:

Зная диаметр окружности выступов, можно определить коэффициент высоты зуба нулевого колеса:

Для проведения этой работы необходимо иметь набор зубчатых колес разных модулей и с разным количеством зубьев и измерительный инструмент — штангенциркуль.

Порядок выполнения работы

1. Подсчитать число зубьев колеса z.
2. По табл. 2.5.1 определить число зубьев z„, которые следует охватить штангенциркулем.
3. Измерить штангенциркулем Wzn и Wzn+ (рис. 2.5.1). Для большей точности обмерять нужно трижды на разных участках зубчатого венца. Окончательные значения Wzn и Wzn+ есть среднеарифметическое трех обмеров. По формуле (2.5.1) определить величину шага рь по основной окружности.
4. По формуле (2.5.2) найти модуль зацепления в миллиметрах, округлив его величину до ближайшего стандартного значения согласно табл. 2.5.2. В формуле 2.5.2 угол исходного контура а = 20°.
5. Учитывая, что есть колеса с углом а = 15°, выполнить проверочный расчет модуля по выражению

измерив диаметр da окружности вершин.

6. Измерить d/диаметр окружности впадин.

Примечание: da и df при четном числе z измерить штангенциркулем (рис. 2.5.2, а), при нечетном числе — найти в соответствии с рис. 2.5.2, б по формулам:

7. Определить:
а) шаг по делительной окружности

б) диаметр делительной окружности

в) диаметр основной окружности

г) делительную высоту головки зуба

д) делительную высоту ножки зуба

е) коэффициент высоты головки зуба

ж) толщину зуба по основной окружности

8. По формуле (2.5.3) рассчитать коэффициент смещения х исходного контура, с которым нарезалось данное колесо.
9. Определить толщину зуба по основной окружности:

Контрольные вопросы и задания

1. Что такое модуль зубчатого колеса?
2. Как определить шаг зубчатого колеса?
3. Дайте понятие основной и делительной окружностей.

4. Какова зависимость между числом зубьев и диаметром зубчатого колеса?
5. Что называется коэффициентом смещения исходного контура?
6. Как изменяются основные параметры зубчатого колеса при смещении исходного контура?

1. Число зубьев z = …
2. Определение шага и модуля зацепления:

Номер измерения	Wz,,+ь мм	Wzn, мм
Среднее

* число zn выбирается по табл. 2.5.1.

Шаг зацепления по основной окружности pb = WZfJ+1 — Wzn = … мм.

Модуль т = ——— = … мм.

Модуль, уточненный по табл. 2.5.2, т = … мм.

Шаг зацепления по делительной окружностир = пт = … мм.

Шаг по основной окружности (уточненный)рь=р cos а= … мм.

3. Диаметр делительной окружности d = mz= … мм.
4. Диаметр основной окружности db = d cos а= … мм.
5. Определение действительной толщины зуба по основной окружности sb = Wzn +1 -znpb = … мм.
6. Расчет толщины зуба по основной окружности нулевого колеса:

7. Определение коэффициента смещения:

9. Определение диаметров окружностей вершин da и впадин df колеса:

Номер измерения	doiB	Н’	da	Н»	df	Расчётные формулы при нечётном числе z
Среднее

10. Учитывая, что есть колеса с углом зацепления а = 15°, в и. 2 выполнить проверочный расчет модуля по выражению (для нормального колеса)

11. Определение коэффициента высоты головки зуба колеса, зубья которого нарезаны без смещения:

Видео:Как определить направление линии зуба косозубой цилиндрической шестерниСкачать

Модуль зуба – Модуль шестерни. Формулы расчёта

Шаг зубьев ρ так же, как и длина окружности, включает в себя трансцендентное число π, а потому шаг — также число трансцендентное. Для удобства расчетов и измерения зубчатых колес в качестве основного расчетного параметра принято рациональное число ρ/π, которое называют модулем зубьев т и измеряют в миллиметрах:

Модулем зубьев т называется часть диаметра делительной окружности, приходящаяся на один зуб. Модуль является основной характеристикой размеров зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым. Для обеспечения взаимозаменяемости зубчатых колес и унификации зуборезного инструмента значения m регламентированы стандартом (табл. 8.1).

Высота головки и ножки зуба. Делительная окружность рассекает зуб по высоте на головку ha и ножку hf. Для создания радиального зазора с (см. рис. 8.19)

Для нормального (некорригированного) зацепления ha = m. Длина активной линии зацепления. При вращении зубчатых колес точка зацепления S (см. рис. 8.9) пары зубьев перемещается по линии зацепления NN.

Зацепление профилей начинается в точке S’ пересечения линии зацепления с окружностью вершин колеса и заканчивается в точке S” пересечения линии зацепления с окружностью вершин шестерни. Отрезок S’S” линии зацепления называется длиной активной линии зацепления и обозначается ga.

Длину ga легко определить графически, для чего радиусами окружностей вершин обоих колес отсекают на линии зацепления NN отрезок S’S” и замеряют ga.

Коэффициент торцового перекрытия. Непрерывность работы зубчатой передачи возможна при условии, когда последующая пара зубьев входит в зацепление до выхода предыдущей, т. е. когда обеспечивается перекрытие работы одной пары зубьев другой. Чем больше пар зубьев одновременно находится в зацеплении, тем выше плавность передачи.

Как определить модуль шестерни с прямым и косым зубом

Часто мне задают вопрос: Как определить модуль косозубой шестерни. Один из самых простых вариантов — обкатать фрезой, то есть методом подбора, вставить в шестерню фрезу и посмотреть совпадает ли шаг! Этот вариант подходит для шестернь малого модуля, для более больших шестернь требуются формулы расчёта.

Давайте определим модуль косозубой шестерни. В качестве примера я возьму небольшую шестерню. Данный метод идентичен и для более больших шестернь и больших модулей.

Есть вот такая шестерня:
Допустим что фрезы обкатать у нас на данный момент нет и вообще хочется просто посчитать по формуле!

Модуль = De/Z+2. То есть диаметр окружности выступов разделить на количество зубьев плюс 2.

Измеряем диаметр:
Диаметр окружности выступов (De) равен 28,6 мм.
Считаем количество зубьев. Z=25.
Делительный диаметр (De) делим на количество зубьев 25 +2. Равно 28,6 разделить на 27=1,05925925925926.
Округляем до ближнего модуля. Получается модуль 1.

Можно использовать и другой вариант — высота зуба делится на 2,25.
Я обычно или обкатываю фрезой или считаю по формуле — модуль = De/Z+2.
Таким образом можно определить модуль как косозубой шестерни, так и шестерни с прямым зубом.
Поделится, добавить в закладки!
zuborez.info

Модуль зубчатого колеса – это… Что такое Модуль зубчатого колеса?

Модуль зубчатого колеса геометрический параметр зубчатых колёс.

Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности dд к числу зубьев z или отношению шага t по делительной окружности к числу: m = dд/z = ts/π.

Для косозубых цилиндрических колёс различают: окружной модуль ms = dд/z = ts/π, нормальный модуль mn = tn/π, осевой модуль ma = tа/π, где ts, tn и ta— соответственно окружной, нормальный и осевой шаги по делительному цилиндру. Значения М. з. к.

стандартизованы, что является основой для стандартизации других параметров зубчатых колёс (геометрические размеры зубчатых колёс выбираются пропорционально модулю) и зуборезного инструмента (см. Зубчатая передача).

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

Модуль высокоэластический
Модуль расстояния

Смотреть что такое “Модуль зубчатого колеса” в других словарях:

МОДУЛЬ ЗУБЧАТОГО КОЛЕСА — геометрический параметр, линейная величина, пропорциональная размерам зубчатого колеса. Различают осевой, окружной и нормальный модуль зубчатого колеса … Большой Энциклопедический словарь
модуль зубчатого колеса — отношение шага зубьев колеса (расстояние между соответствующими точками соседних зубьев, измеренное по дуге окружности) к числу π. Значения модуля зубчатого колеса стандартизованы. Геометрические размеры зубчатых колёс выбираются пропорционально… … Энциклопедический словарь
нормальный модуль зубьев конического зубчатого колеса — (mn) нормальный модуль Линейная величина, в раз меньшая нормального шага зубьев конического зубчатого колеса. Примечания 1. Различают нормальные модули: внешний (mne), средний (mnm), внутренний (mni) и др. (mnx) делительные; внешний (mnwe),… … Справочник технического переводчика
нормальный модуль цилиндрического зубчатого колеса — (mn) модуль Делительный нормальный модуль зубьев цилиндрического зубчатого колеса, принимаемый в качестве расчетного и равный модулю нормального исходного контура. Примечание В случаях, исключающих возможность возникновения недоразумений, индекс… … Справочник технического переводчика
окружной модуль зубьев конического зубчатого колеса — (mt) окружной модуль Линейная величина, в раз меньшая окружного шага зубьев конического зубчатого колеса. Примечание Различают окружные модули: внешний (mte), средний (mtm), внутренний (mti) и др. (mtx) делительные; внешний (mtwe), средний (mtwm) … Справочник технического переводчика
расчетный модуль конического зубчатого колеса — расчетный модуль Окружной или нормальный делительный модуль в расчетном сечении. Примечания 1. Расчетный модуль конического зубчатого колеса из семейства сопряженных конических зубчатых колес, форма и размеры зубьев которых определяются парой… … Справочник технического переводчика
Нормальный модуль цилиндрического зубчатого колеса т n — 2.1.2. Нормальный модуль цилиндрического зубчатого колеса т n Модуль Делительный нормальный модуль зубьев цилиндрического зубчатого колеса, принимаемый в качестве расчетного и равный модулю нормального исходного контура. Примечание. В случаях,… … Словарь-справочник терминов нормативно-технической документации
Нормальный модуль зубьев конического зубчатого колеса — 67. Нормальный модуль зубьев конического зубчатого колеса Нормальный модуль mn Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения … Словарь-справочник терминов нормативно-технической документации
Окружной модуль зубьев конического зубчатого колеса — 59. Окружной модуль зубьев конического зубчатого колеса Окружной модуль mt Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения … Словарь-справочник терминов нормативно-технической документации
Расчетный модуль конического зубчатого колеса — 146. Расчетный модуль конического зубчатого колеса Расчетный модуль Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения оригинал документа … Словарь-справочник терминов нормативно-технической документации

Модуль зуба что такое

Модуль зубьев зубчатого колеса

Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня».

За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки.

Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.

Что такое модуль зубчатого колеса

Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров

диаметр;
число зубьев;
шаг;
высота зубца;
и некоторые другие.

Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.

Скачать ГОСТ 9563-60

В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.

Для расчета этого параметра применяют следующие формулы:
m=t/π,
где t — шаг.

Параметры зубчатых колес
Модуль зубчатого колеса можно рассчитать и следующим образом:
m=h/2,25,
где h — высота зубца.
И, наконец,
m=De/(z+2),
где De — диаметр окружности выступов,а z — число зубьев.

Что же такое модуль шестерни?

это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса
Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
π×D=t×z,
проведя преобразование, получим:
D=(t /π)×z

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

t/π=m,
размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
В=m×z;
выполнив преобразование, находим:
m=D / z.
Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным
De=d+2× h’,
где h’- высота головки.
Высоту головки приравнивают к m:
h’=m.
Проведя математические преобразования с подстановкой, получим:
De=m×z+2m = m(z+2),
откуда вытекает:
m=De/(z+2).
Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:
Di=D-2h“,
где h“- высота ножки зубца.
Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:
h’ = 1,25m.

Устройство зубчатого колеса
Выполнив подстановку в правой части равенства, имеем:
Di = m×z-2×1,25m = m×z-2,5m;
что соответствует формуле:
Di = m(z-2,5m).
Полная высота:
h = h’+h“,
и если выполнить подстановку, то получим:
h = 1m+1,25m=2,25m.
Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
Следующий важный размер, толщину зубца s принимают приблизительно равной:

для отлитых зубцов: 1,53m:
для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины

для отлитых зубцов: sв=πm-1,53m=1,61m:
для выполненных путем фрезерования- sв= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

усилия, прикладываемые к детали при эксплуатации;
конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Исходные данные и замеры

На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.

Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.

Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.

Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.

Результаты расчетов

Для более крупных потребуются измерения и вычисления.

Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:

m=De/(z+2)

Последовательность действий следующая:

измерить диаметр штангенциркулем;
сосчитать зубцы;
разделить диаметр на z+2;
округлить результат до ближайшего целого числа.

Зубец колеса и его параметры

Данный метод подходит как для прямозубых колес, так и для косозубых.

Расчет параметров колеса и шестерни косозубой передачи

Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.

Видео:Лекция 4. Конические зубчатые передачиСкачать

Расчёт модулей зубчатых колёс

Перейти к загрузке файла

Ориентировочное минимально допустимое значение модуля m, мм. определим по формуле: где km — вспомогательный коэффициент; М1 — крутящий момент на шестерне, Н•м; z1 — число зубьев шестерни; kFв — коэффициент учитывающий неравномерность распределения нагрузки по ширине венца; шbd — отношение ширины венца к начальному диаметру шестерни; yF1 — коэффициент учитывающий форму зуба. Допустимое напряжение зубьев по изгибу уFP определяют по формуле у’FP — допускаемое напряжение зубьев по изгибу, МПа, соответствующее базовому числу циклов перемены напряжений; kFL — коэффициент долговечности. Ориентировочное минимально допустимое значение модуля: Рассчитанный по формуле модуль округляется до стандартного значения m=2. Характеристики зубчатых колёс сведём в таблицу:
№ зубчатого колеса Число зубьев Модуль, мм Диаметр делительной окружности, мм Ширина зубчатого венца, мм
1 18 2 36 52
2 36 2 72 52
3 20 2 40 52
4 50 2 100 52
5 35 2 70 52
6 35 2 70 52
7 20 2 40 65
8 64 2 128 65
9 56 2 112 65
10 28 2 56 65
Расчёт на контактную выносливость рабочих поверхностей зубьев
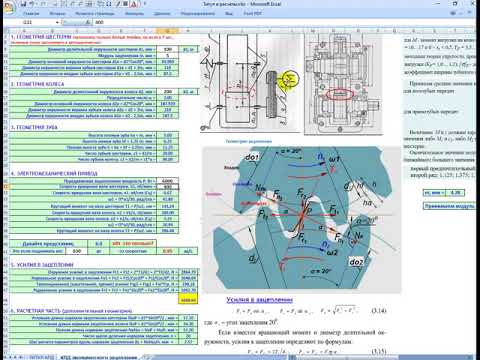
Действующие в передаче контактные напряжения определяют по формуле
где ун — контактные напряжения, МПа; zН — коэффициент, зависящий от угла наклона зубьев, для x=0 применяем zН=1,76; zМ — коэффициент, учитывающий механические свойства материалов сопряжённых колёс, для стальных колёс zМ=275; zе — коэффициент, учитывающий суммарную длину контактных линий:
Коэффициент торцевого перекрытия:
где z1 и z2 — числа зубьев шестерни и колеса, знак «+» принимают для наружного зацепления.
Удельную расчётную окружную силу щHt определяют по формуле
где Pt — исходная окружная сила, Н:
где щHV — удельная окружная динамическая сила, Н/мм,
где V — окружная скорость, м/с; ащ — межосевое расстояние, мм.
Допускаемое контактное напряжение [ун] определяем по формуле:
где — допускаемое контактное напряжение, соответствующее базовому числу циклов перемены напряжений, МПа; kHL — коэффициент долговечности, для зубчатых колёс коробки скоростей станков kHL=1.
Для стали 45 с улучшением =750 МПа.
532,25 МПа ? 750 МПа
Условие контактной выносливости выполняется.
Расчёт на изгибную выносливость зубьев
Действующее в передаче напряжение изгиба сравнивается с допустимыми, с учётом коэффициента долговечности.
Действующее напряжение изгиба:
Коэффициент yе — учитывает перекрытие зубьев. Для прямозубых колёс применяют yе=1. Коэффициент yв учитывает наклон зуба. Для прямозубых применяют yв=1.
Удельную расчётную окружную силу щFt определяем по формуле
где Pt — расчётная окружная сила в зубчатом зацеплении, Н; bщ — рабочая ширина венца, мм
Окружная сила Pt=2•103•M1/d1, где M1 — крутящий момент, Н•м; d1 — диаметр делительной окружности, мм.
Коэффициент kFa учитывает распределение нагрузки между зубьями. Для прямозубых передач приметаем kFa=1. Коэффициент kFв учитывает распределение нагрузки по ширине венца, можно принять kFв=1.1.
Коэффициент kFv учитывает динамическую нагрузку, возникающую в зацеплении.
где щFV — удельная окружная динамическая сила, Н/мм,
где V — окружная скорость, м/с; ащ — межосевое расстояние, мм; для прямозубых передач д=0.016; коэффициент g =47, учитывает влияние разности шагов зацепления.
Допускаемое изгибное напряжении [уF] определяется по формуле:
где — допускаемое контактное напряжение, соответствующее базовому числу циклов перемены напряжений, МПа; kFL — коэффициент долговечности, для зубчатых колёс коробки скоростей станков kFL=1.
Для стали Для стали 45 с улучшением у‘F=450 МПа, условие изгибной выносливости выполняется.
265.49 МПа ? 450 МПа
Условие на изгибную выносливость выполняется.
Видео:Как определить шестернюСкачать
Диаметр делительной окружности косозубого цилиндрического колеса
ъХВЮБФБС РЕТЕДБЮБ — ЬФП НЕИБОЙЪН, ЛПФПТЩК У РПНПЭША ЪХВЮБФПЗП ЪБГЕРМЕОЙЕ РЕТЕДБЕФ ЙМЙ РТЕПВТБЪХЕФ ДЧЙЦЕОЙЕ У ЙЪНЕОЕОЙЕН ХЗМПЧЩИ УЛПТПУФЕК Й НПНЕОФПЧ.
ъХВЮБФЩЕ РЕТЕДБЮЙ РТЙНЕОСАФ ДМС РТЕПВТБЪПЧБОЙС Й РЕТЕДБЮЙ ЧТБЭБФЕМШОПЗП ДЧЙЦЕОЙС НЕЦДХ ЧБМБНЙ У РБТБММЕМШОЩНЙ, РЕТЕУЕЛБАЭЙНЙУС Й РЕТЕЛТЕЭЙЧБАЭЙНЙУС ПУСНЙ, Б ФБЛЦЕ ДМС РТЕПВТБЪПЧБОЙС ЧТБЭБФЕМШОПЗП ДЧЙЦЕОЙС Ч РПУФХРБФЕМШОПЕ Й ОБПВПТПФ.
ъХВЮБФЩЕ РЕТЕДБЮЙ НЕЦДХ РБТБММЕМШОЩНЙ ЧБМБНЙ ПУХЭЕУФЧМСАФУС ГЙМЙОДТЙЮЕУЛЙНЙ ЛПМЕУБНЙ У РТСНЩНЙ, ЛПУЩНЙ Й ЫЕЧТПООЩНЙ ЪХВШСНЙ (ТЙУХОПЛ 55, Б-З). рЕТЕДБЮЙ НЕЦДХ ЧБМБНЙ У РЕТЕУЕЛБАЭЙНЙУС ПУСНЙ ПУХЭЕУФЧМСАФУС ПВЩЮОП ЛПОЙЮЕУЛЙНЙ ЛПМЕУБНЙ У РТСНЩНЙ Й ЛТХЗПЧЩНЙ ЪХВШСНЙ (ТЙУХОПЛ 55, Б-Ъ), ТЕЦЕ ФБОЗЕОГЙБМШОЩНЙ ЪХВШСНЙ (ТЙУХОПЛ 55, Ц). ъХВЮБФЩЕ РЕТЕДБЮ ДМС РТЕПВТБЪПЧБОЙС ЧТБЭБФЕМШОПЗП ДЧЙЦЕОЙС Ч РПУФХРБФЕМШОПЕ Й ОБПВПТПФ ПУХЭЕУФЧМСАФУС ГЙМЙОДТЙЮЕУЛЙН ЛПМЕУПН Й ТЕКЛПК (ТЙУХОПЛ 55, Д).
дМС ЧБМПЧ У РЕТЕЛТЕЭЙЧБАЭЙНЙУС ПУСНЙ РТЙНЕОСАФ ЪХВЮБФП-ЧЙОФПЧЩЕ РЕТЕДБЮЙ.
ъХВЮБФЩЕ РЕТЕДБЮЙ УПУФБЧМСАФ ОБЙВПМЕЕ ТБУРТПУФТБОЕООХА Й ЧБЦОХА ЗТХРРХ НЕИБОЙЮЕУЛЙИ РЕТЕДБЮ. чЩРХУЛ ЪХВЮБФЩИ ЛПМЕУ Ч тПУУЙЙ ЙЪНЕТСЕФУС НОПЗЙНЙ УПФОСНЙ НЙММЙПОПЧ Ч ЗПД. йИ РТЙНЕОСАФ Ч ЫЙТПЛПН ДЙБРБЪПОЕ ПВМБУФЕК Й ХУМПЧЙК ТБВПФЩ; ПФ ЮБУПЧ Й РТЙВПТПЧ ДП УБНЩИ ФСЦЕМЩИ НБЫЙО, ДМС РЕТЕДБЮЙ ПЛТХЦОЩИ УЙМ ПФ НЙММЙОШАФПОПЧ ДП ДЕУСФЛПЧ НЕЗБОШАФПОПЧ, ДМС НПНЕОФПЧ ДП 10 7 ОШАФПОПЧ ОБ НЕФТ Й НПЭОПУФЕК ПФ ОЙЮФПЦОП НБМЩИ ДП ДЕУСФЛПЧ ФЩУСЮ ЛЙМПЧБФФ, У ДЙБНЕФТБНЙ ЛПМЕУ ПФ ДПМЕК НЙММЙНЕФТБ ДП 10 Н Й ВПМЕЕ.
тЙУХОПЛ 55 — пУОПЧОЩЕ ЧЙДЩ ЪХВЮБФЩИ РЕТЕДБЮ.
ъХВЮБФЩЕ РЕТЕДБЮЙ Ч УТБЧОЕОЙЙ У ДТХЗЙНЙ НЕИБОЙЮЕУЛЙНЙ РЕТЕДБЮБНЙ ПВМБДБАФ УХЭЕУФЧЕООЩНЙ ДПУФПЙОУФЧБНЙ, Б ЙНЕООП:
НБМЩНЙ ЗБВБТЙФБНЙ;
ЧЩУПЛЙН лрд;
ВПМШЫПК ОБДЕЦОПУФША Ч ТБВПФЕ;
РПУФПСОУФЧПН РЕТЕДБФПЮОПЗП ПФОПЫЕОЙС ЙЪ-ЪБ ПФУХФУФЧЙС РТПУЛБМШЪЩЧБОЙС;
ЧПЪНПЦОПУФША РТЙНЕОЕОЙС Ч ЫЙТПЛПН ДЙБРБЪПОЕ НПНЕОФПЧ, УЛПТПУФЕК Й РЕТЕДБФПЮОЩИ ПФОПЫЕОЙК.
л ОЕДПУФБФЛБН ЪХВЮБФЩИ РЕТЕДБЮ НПЗХФ ВЩФШ ПФОЕУЕОЩ ФТЕВПЧБОЙС ЧЩУПЛПК ФПЮОПУФЙ ЙЪЗПФПЧМЕОЙС Й ЫХН РТЙ ТБВПФЕ УП ЪОБЮЙФЕМШОЩНЙ УЛПТПУФСНЙ.
зЕПНЕФТЙС Й ЛЙОЕНБФЙЛБ ЬЧПМШЧЕОФОЩИ ЪБГЕРМЕОЙК
пУОПЧОЩН ЛЙОЕНБФЙЮЕУЛЙН ХУМПЧЙЕН, ЛПФПТПНХ ДПМЦОЩ ХДПЧМЕФЧПТСФШ РТПЖЙМЙ ЪХВШЕЧ, СЧМСЕФУС РПУФПСОУФЧП НЗОПЧЕООПЗП РЕТЕДБФПЮОПЗП ПФОПЫЕОЙС РЕТЕДБЮЙ. ьФПНХ ХУМПЧЙА ХДПЧМЕФЧПТСАФ НОПЗЙЕ ЛМБУУЩ ЛТЙЧЩИ. дМС ПВЕУРЕЮЕОЙС ЧЩУПЛПЗП лрд, РТПЮОПУФЙ Й ДПМЗПЧЕЮОПУФЙ ЛПМЕУ РТПЖЙМЙ ДПМЦОЩ ПВЕУРЕЮЙЧБФШ НБМЩЕ УЛПТПУФЙ УЛПМШЦЕОЙС Й ДПУФБФПЮОЩЕ ТБДЙХУЩ ЛТЙЧЙЪОЩ Ч ФПЮЛБИ ЛПОФБЛФБ. рТПЖЙМЙ ДПМЦОЩ ДПРХУЛБФШ МЕЗЛПЕ ЙЪЗПФПЧМЕОЙЕ, Ч ЮБУФОПУФЙ ОБТЕЪБОЙЕ РТПУФЩН ЙОУФТХНЕОФПН ОЕЪБЧЙУЙНП ПФ ЮЙУМБ ЪХВШЕЧ ЛПМЕУ. ьФЙН ХУМПЧЙСН ОБЙВПМЕЕ РПМОП ХДПЧМЕФЧПТСЕФ ЬЧПМШЧЕОФОПЕ ЪБГЕРМЕОЙЕ, ОБЫЕДЫЕЕ ЫЙТПЮБКЫЕЕ РТЙНЕОЕОЙЕ Ч НБЫЙОПУФТПЕОЙЙ.
лБЦДПЕ ЬЧПМШЧЕОФОПЕ ЪХВЮБФПЕ ЛПМЕУП ДПМЦОП ВЩФШ ОБТЕЪБОП ФБЛ, ЮФПВЩ ПОП НПЗМП ЧИПДЙФШ Ч ЪБГЕРМЕОЙЕ У ЛПМЕУБНЙ ФПЗП ЦЕ НПДХМС, ЙНЕАЭЙНЙ МАВПЕ ЮЙУМП ЪХВШЕЧ. ьЧПМШЧЕОФОПЕ ЪБГЕРМЕОЙЕ НБМП ЮХЧУФЧЙФЕМШОП Л ПФЛМПОЕОЙСН НЕЦПУЕЧПЗП ТБУУФПСОЙС. ьЧПМШЧЕОФОЩЕ ЪХВЮБФЩЕ ЛПМЕУБ НПЗХФ ОБТЕЪБФШУС РТПУФЩН ЙОУФТХНЕОФПН: ПОЙ ХДПВОЩ ДМС ЛПОФТПМС.
ъБГЕРМЕОЙЕ ЪХВЮБФЩИ ЛПМЕУ ЬЛЧЙЧБМЕОФОП ЛБЮЕОЙА ВЕЪ УЛПМШЦЕОЙС ПЛТХЦОПУФЕК У ДЙБНЕФТБНЙ dw1 Й dw2 (ТЙУХОПЛ 56), ОБЪЩЧБЕНЩИ ОБЮБМШОЩНЙ ПЛТХЦОПУФСНЙ. рТЙ ЛБЮЕОЙЙ ВЕЪ УЛПМШЦЕОЙС РТСНПК NN (ТЙУХОПЛ 56) РП ПУОПЧОЩН ПЛТХЦОПУФСН У ДЙБНЕФТБНЙ db1=dw1 cosαtw Й db2=dw2 cosαtw (ЗДЕ αtw — ХЗПМ ЪБГЕРМЕОЙС) ФПЮЛЙ ЬФПК РТСНПК ПРЙУЩЧБАФ ОБ ЛБЦДПН ЙЪ ЛПМЕУ ЬЧПМШЧЕОФЩ. рПЬФПНХ ОХЦОПЕ ДЧЙЦЕОЙЕ ЛПМЕУ НПЦОП РПМХЮЙФШ ЪБГЕРМЕОЙЕН ЪХВШЕЧ, ПЮЕТЮЕООЩИ РП ЬЧПМШЧЕОФБН. рТЙ ХЧЕМЙЮЕОЙЙ ЮЙУМБ ЪХВШЕЧ ДП ВЕУЛПОЕЮОПУФЙ ЬЧПМШЧЕОФБ РТЕЧТБЭБЕФУС Ч РТСНХА, Б ЪХВЮБФПЕ ЛПМЕУП — Ч ТЕКЛХ У ФТБРЕГЙЕЧЙДОЩН РТПЖЙМЕН ЪХВШЕЧ, ХДПВОХА ДМС ЙЪЗПФПЧМЕОЙС Й ЛПОФТПМС. рПЬФПНХ Ч ЛБЮЕУФЧЕ ЙУИПДОПЗП ЛПОФХТБ ДМС ЬЧПМШЧЕОФОПЗП ЪБГЕРМЕОЙС РТЙОСФБ ТЕКЛБ, Й ЫЙТПЛПЕ РТЙНЕОЕОЙЕ ОБЫМП ЖПТНППВТБЪПЧБОЙЕ ЪХВШЕЧ Ч РТПГЕУУЕ ЪБГЕРМЕОЙС У ТЕЕЮОЩН ЙОУФТХНЕОФПН.
тЙУХОПЛ 56 — пВТБЪПЧБОЙЕ ЬЧПМШЧЕОФОЩИ РТПЖЙМЕК.
ч ЛБЮЕУФЧЕ ПУОПЧОПЗП РБТБНЕФТБ ЪХВЮБФПЗП ЪБГЕРМЕОЙС РТЙОСФ НПДХМШ ЪХВШЕЧ m — ЧЕМЙЮЙОБ, РТПРПТГЙПОБМШОБС ЫБЗХ Т РП ДЕМЙФЕМШОПНХ ГЙМЙОДТХ, Ф. Е. ГЙМЙОДТХ, ОБ ЛПФПТПН ЫБЗ ЪХВЮБФПЗП ЛПМЕУБ ТБЧЕО ЫБЗХ ЙУИПДОПЗП ЛПОФХТБ, Ф. Е. ЫБЗХ РТПЙЪЧПДСЭЕК ТЕКЛЙ. фБЛЙН ПВТБЪПН, m=Т/π.
ыБЗ Т, ФБЛ ЦЕ ЛБЛ Й ДМЙОБ ПЛТХЦОПУФЙ, СЧМСЕФУС ЛТБФОЩН ЮЙУМХ π Й РПЬФПНХ ОЕХДПВОЩН ДМС РТЙОСФЙС ЪБ ПУОПЧОПК РБТБНЕФТ ЪБГЕРМЕОЙС.
ч ПВЭЕН УМХЮБЕ ДМС ЛПУПЪХВЩИ РЕТЕДБЮ ТБУУНБФТЙЧБАФ ПЛТХЦОЩЕ Й ОПТНБМШОЩЕ ЫБЗЙ Й УППФЧЕФУФЧЕООП НПДХМЙ.
пЛТХЦОПК ДЕМЙФЕМШОЩК ЫБЗ Т_t — ЬФП ТБУУФПСОЙЕ НЕЦДХ ПДОПЙНЕООЩНЙ РТПЖЙМСНЙ УПУЕДОЙИ ЪХВШЕЧ, ЙЪНЕТЕООПЕ РП ДХЗЕ ДЕМЙФЕМШОПК ПЛТХЦОПУФЙ ЪХВЮБФПЗП ЛПМЕУБ. пЮЕЧЙДОП, ЮФП:
уППФЧЕФУФЧЕООП ПЛТХЦОПК НПДХМШ:
Ф. Е. РТЕДУФБЧМСЕФ УПВПК ЮБУФОПЕ ПФ ДЕМЕОЙС ДЙБНЕФТБ ДЕМЙФЕМШОПК ПЛТХЦОПУФЙ ОБ ЮЙУМП ЪХВШЕЧ.
оПТНБМШОЩК ЫБЗ Т_n — ЛТБФЮБКЫЕЕ ТБУУФПСОЙЕ РП ДЕМЙФЕМШОПНХ ГЙМЙОДТХ НЕЦДХ ПДОПЙНЕООЩНЙ РТПЖЙМШОЩНЙ РПЧЕТИОПУФСНЙ ДЧХИ УНЕЦОЩИ ЪХВШЕЧ:
ЗДЕ ß — ХЗПМ ОБЛМПОБ МЙОЙЙ ЪХВШЕЧ РП ДЕМЙФЕМШОПНХ ГЙМЙОДТХ.
уППФЧЕФУФЧЕООП ОПТНБМШОЩК НПДХМШ m:
дМС РТСНПЪХВЩИ РЕТЕДБЮ ПЛТХЦОЩЕ Й ОПТНБМШОЩЕ ЫБЗЙ Й НПДХМЙ УППФЧЕФУФЧЕООП УПЧРБДБАФ.
нПДХМЙ УФБОДБТФЙЪПЧБОЩ Ч ДЙБРБЪПОЕ 0,05. 100 НН (зпуф 9563-80*). оЙЦЕ ДБОЩ НПДХМЙ, НН, Ч ОБЙВПМЕЕ ХРПФТЕВЙФЕМШОПН ДЙБРБЪПОЕ (1-К ТСД УМЕДХЕФ РТЕДРПЮЙФБФШ 2-НХ):
1-К РТЕДРПЮФЙФЕМШОЩК ТСД:1; 1,25; 1,5; 2; 2,5;3; 4; 5; 6; 8; 10; 12;16; 20; 25; 32; 40
2-К РТЕДРПЮФЙФЕМШОЩК ТСД: 1,125; 1,375; 1,75;2,25; 2,75; 3,5; 4,5;5,5; 7; 9; 11; 14; 18;22: 28; 36; 45
дМС ТЕДХЛФПТПЧ ФБЛЦЕ ДПРХУЛБАФ НПДХМЙ 1,6; 3,15; 6,3; 12,5 НН.
дМС ЛПУПЪХВЩИ ГЙМЙОДТЙЮЕУЛЙИ ЛПМЕУ УФБОДБТФОЩНЙ ОБЪОБЮБАФ ОПТНБМШОЩЕ НПДХМЙ. рБТБНЕФТЩ ЙУИПДОПЗП ЛПОФХТБ ГЙМЙОДТЙЮЕУЛЙИ ЪХВЮБФЩИ ЛПМЕУ УФБОДБТФЙЪПЧБОЩ (зпуф 13755-81):
ХЗПМ РТПЖЙМС α =20њ;
ЧЩУПФБ ЗПМПЧЛЙ ЪХВБ h_a=h_a*m, h_a*=1;
ЗМХВЙОБ ЪБИПДБ ЪХВШЕЧ h_z=2m;
ТБДЙБМШОЩК ЪБЪПТ НЕЦДХ ЪХВШСНЙ У=0,25m (РТЙ ОБТЕЪБОЙЙ ДПМВСЛБНЙ ДП 0,35m);
ТБДЙХУ ЧЩЛТХЦЛЙ Х ЛПТОС ЪХВБ Т_f=0,38m (ТЙУХОПЛ 57, Б).
тЙУХОПЛ 57 — йУИПДОЩК ЛПОФХТ.
дМС ВЩУФТПИПДОЩИ ЪХВЮБФЩИ РЕТЕДБЮ Ч ГЕМСИ ХНЕОШЫЕОЙС УЙМ ХДБТБ РТЙ ЧИПДЕ ЪХВШЕЧ Ч ЪБГЕРМЕОЙЕ Й ЧЩИПДЕ ЙИ ЙЪ ЪБГЕРМЕОЙС Й ДМС ХНЕОШЫЕОЙС ЫХНБ РТЙНЕОСАФ НПДЙЖЙЛБГЙА РТПЖЙМС ЗПМПЧЛЙ ЪХВБ (ЖМБОЛЙТПЧБОЙЕ). жМБОЛЙТПЧБОЙЕ РТЕДУФБЧМСЕФ УПВПК РТЕДОБНЕТЕООПЕ ПФЛМПОЕОЙЕ ПФ ЬЧПМШЧЕОФЩ РТПЖЙМС Х ЧЕТЫЙО ЪХВШЕЧ (ОБ ЮБУФЙ ЧЩУПФЩ ЗПМПЧЛЙ), ОБРТБЧМЕООПЕ Ч ФЕМП ЪХВШЕЧ. жМБОЛЙТПЧБОЙЕ ХНЕОШЫБЕФ УЙМЩ ХДБТБ, УЧСЪБООЩЕ У ДЕЖПТНБГЙЕК ЪХВШЕЧ Й ПЫЙВЛБНЙ ПУОПЧОПЗП ЫБЗБ.
дМС ЖМБОЛЙТПЧБООЩИ ЛПМЕУ РТЕДХУНПФТЕО ЙУИПДОЩК ЛПОФХТ, Х ЛПФПТПЗП ЛБЦДБС ВПЛПЧБС УФПТПОБ ЪХВБ ПЮЕТЮЕОБ ДЧХНС РТСНЩНЙ (ТЙУХОПЛ 57, В) ЙМЙ РТСНПК Й ДХЗПК.
пУОПЧОЩЕ ЗЕПНЕФТЙЮЕУЛЙЕ УППФОПЫЕОЙС РТЙЧЕДЕОЩ Ч ФБВМЙГЕ 13. оБЪЧБОЙС Й ПВПЪОБЮЕОЙС ЬМЕНЕОФПЧ ЪХВЮБФПЗП ЪБГЕРМЕОЙС РПЛБЪБОЩ ОБ ТЙУХОЛЕ 58.
тЙУХОПЛ 58 — ьМЕНЕОФЩ ЪХВЮБФПЗП ЪБГЕРМЕОЙС.
рБТБНЕФТЩ Й ЛПОУФТХЛГЙЙ ЪХВЮБФЩИ РЕТЕДБЮ
рЕТЕДБФПЮОЩЕ ЮЙУМБ u=z₂/ z₁ ПВЩЮОП ПЗТБОЙЮЙЧБАФУС ЗБВБТЙФБНЙ РЕТЕДБЮ. ч ТЕДХЛФПТОЩИ РЕТЕДБЮБИ НБЛУЙНБМШОЩЕ ЪОБЮЕОЙС РЕТЕДБФПЮОЩИ ЮЙУЕМ ФЙИПИПДОПК Й РТПНЕЦХФПЮОПК РЕТЕДБЮЙ 5,6. 6,3, ВЩУФТПИПДОПК РЕТЕДБЮЙ 6,3. 8.
оЙЦОЙЕ ЪОБЮЕОЙС РТЙ ФЧЕТДПУФЙ 56. 63оRуЬ, ЧЕТИОЙЕ — РТЙ ≤350оч. йНЕЕФУС ФЕОДЕОГЙС УОЙЦЕОЙС Й РТЙ ЧЩУПЛПК ФЧЕТДПУФЙ ЪХВШЕЧ ДП 5.
ч ЛПТПВЛБИ УЛПТПУФЕК УФБОЛПЧ u≤4; Ч РТЙЧПДБИ УФПМПЧ ВПМШЫЙИ ДЙБНЕФТПЧ u≤20. оПНЙОБМШОЩЕ РЕТЕДБФПЮОЩЕ ЮЙУМБ ГЙМЙОДТЙЮЕУЛЙИ ЪХВЮБФЩИ РЕТЕДБЮ УФБОДБТФЙЪПЧБОЩ РП уф уьч 312-76:
1-К РТЕДРПЮФЙФЕМШОЩК ТСД1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12
2-К РТЕДРПЮФЙФЕМШОЩК ТСД1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11
нЙОЙНБМШОПЕ ЮЙУМП ЪХВШЕЧ ЫЕУФЕТЕО ПВЩЮОП ПЗТБОЙЮЙЧБЕФУС ХУМПЧЙЕН ОЕ РПДТЕЪБОЙС ЪХВШЕЧ Х ПУОПЧБОЙС. дМС ОЕЛПТТЙЗЙТПЧБООЩИ РЕТЕДБЮ zmin=17, ДМС ЛПТТЙЗЙТПЧБООЩИ zmin=12. 14 Й НЕОШЫЕ. рТЕЙНХЭЕУФЧЕООП ЮЙУМБ ЪХВШЕЧ ЧЩВЙТБАФ ЙЪ ЛЙОЕНБФЙЮЕУЛЙИ ХУМПЧЙК.
вПМШЫПЕ ЪОБЮЕОЙЕ ДМС ПЗТБОЙЮЕОЙС ОПНЕОЛМБФХТЩ ЛПТРХУОЩИ ДЕФБМЕК ТЕДХЛФПТПЧ Й ЛПТПВПЛ УЛПТПУФЕК ЙНЕЕФ УФБОДБТФЙЪБГЙС НЕЦПУЕЧЩИ ТБУУФПСОЙК РЕТЕДБЮ.
фБВМЙГБ 13 — пУОПЧОЩЕ ЗЕПНЕФТЙЮЕУЛЙЕ ЪБЧЙУЙНПУФЙ ГЙМЙОДТЙЮЕУЛЙИ ЪХВЮБФЩИ РЕТЕДБЮ.
рБТБНЕФТ ЪБГЕРМЕОЙС зЕПНЕФТЙЮЕУЛЙЕ ЪБЧЙУЙНПУФЙ РТЙ ЪБГЕРМЕОЙЙ
вЕЪ УНЕЭЕОЙС ЙУИПДОПЗП ЛПОФХТБ уП УНЕЭЕОЙЕН ЙУИПДОПЗП ЛПОФХТБ
нЕЦПУЕЧПЕ ТБУУФПСОЙЕ
лПЬЖЖЙГЙЕОФ ХТБЧОЙФЕМШОПЗП УНЕЭЕОЙС ∆y зДЕ y=x₂±x₁-∆y
чЩУПФБ ЪХВБ h=2,25m h=2,25m-∆ym
тБДЙБМШОЩК ЪБЪПТ c=0,25m c=0,25m
дЙБНЕФТЩ:
дЕМЙФЕМШОЩЕ d₁; d₂ d₁=mz₁/cosß
d₂=mz₂/cosß
оБЮБМШОЩЕ d_ω1;d_ω2 d_ω1= d₁
d_ω2= d₂ d_ω2= d₁u
дЙБНЕФТ ЧЕТЫЙО ЪХВШЕЧ:ЧОЕЫОЕЗП ЪБГЕРМЕОЙС d_a1=d₁+2md_a2=d₂+2m d_a1=d₁+2(1+x₁-∆y)md_a2=d₂+2(1+x₂-∆y)m
чОХФТЕООЕЗП ЪБГЕРМЕОЙС d_a1=d₁+2m d_a2=d₂-2m d_a1=d₁+2(1+x₁)m d_a2=d₂-2(0,75-0,875x₂+∆y)m РТЙ x₂ тЙУХОПЛ 59 — лПОУФТХЛГЙЙ ЪХВЮБФЩИ ЛПМЕУ. тЙУХОПЛ 60 — вМПЛЙ ЫЕУФЕТЕО Й РЕТЕДЧЙЦОЩЕ ЫЕУФЕТОЙ.
фПМЭЙОХ ЧЕОГПЧ ДП ЧРБДЙО ХМХЮЫЕООЩИ ЛПМЕУ ЧЩВЙТБАФ ТБЧОПК (2. 3)m_t, ФПМЭЙОХ ДЙУЛПЧ ТБЧОПК (0,2:0,3)b,ДЙБНЕФТЩ УФХРЙГГ — (1,6. 1,9)d_Ч (ЗДЕ b — ЫЙТЙОБ ЛПМЕУБ; d_Ч—ДЙБНЕФТ ЧБМБ). чОХФТЕООСС РПЧЕТИОПУФШ ПВПДБ Й ОБТХЦОБС РПЧЕТИОПУФШ УФХРЙГЩ, ОЕ ПВТБВБФЩЧБЕНЩЕ НЕИБОЙЮЕУЛЙ, ЙНЕАФ ХЛМПОЩ. ъХВЮБФЩЕ ЛПМЕУБ У ФЧЕТДЩНЙ ЪХВШСНЙ РТЕЙНХЭЕУФЧЕООП ДЕМБАФ У ОЕВПМШЫЙНЙ ЧЩЕНЛБНЙ РП ФПТГБН. фЕИОПМПЗЙЮОБС ЛПОУФТХЛГЙС ЫФБНРПЧБООПЗП ЛПМЕУБ РПЛБЪБОБ ОБ ТЙУХОПЛ 59, З.
юЙУМП РПФТЕВОЩИ ФЙРПТБЪНЕТПЧ ЛПМЕУ УЙМШОП ЧПЪТБУФБЕФ ЙЪ-ЪБ НОПЗППВТБЪЙС ЖПТН УФХРЙГ, ДЙБНЕФТПЧ ЧБМПЧ Й Ф. Д. рПЬФПНХ ВЩМП РТЕДМПЦЕОП УФБОДБТФЙЪПЧБФШ Й ГЕОФТБМЙЪПЧБООП ЙЪЗПФПЧМСФШ ЪХВЮБФЩЕ ЧЕОГЩ, ЛПФПТЩЕ РПФПН РТЙУПЕДЙОСФШ, Ч ЮБУФОПУФЙ РТЙЛМЕЙЧБФШ, Л УФХРЙГБН (ТЙУХОПЛ 61, Б). ьФП ФБЛЦЕ РПЪЧПМСЕФ ЫМЙЖПЧБФШ ЪХВШС ВМПЛПЧ ЫЕУФЕТЕО ВЕЪ ХЧЕМЙЮЕОЙС ЙИ ПУЕЧЩИ ЗБВБТЙФПЧ (ТЙУХОПЛ 61, В).
тЙУХОПЛ 61 — лМЕЕОЩЕ ЪХВЮБФЩЕ ЛПМЕУБ.
лПОУФТХЛГЙЙ ЛТХРОЩИ ЛПМЕУ:
гЕМШОПМЙФЩЕ ЛПМЕУБ ЙНЕАФ ТБУРТПУФТБОЕОЙЕ ЛБЛ ОБЙНЕОЕЕ ФТХДПЕНЛЙЕ. рП УЧПЕК ОЕУХЭЕК УРПУПВОПУФЙ ПОЙ ХУФХРБАФ ЛПМЕУБН У ЛПЧБОЩН ЙМЙ РТПЛБФБООЩН ПВПДПН. дП ДЙБНЕФТБ 900 НН ЙИ РТЕЙНХЭЕУФЧЕООП ЧЩРПМОСАФ ПДОПДЙУЛПЧЩНЙ (ТЙУХОПЛ 62,Б..Ч), Б РТЙ ВПМШЫЙИ ДЙБНЕФТБИ Й ЫЙТЙОЕ — ДЧХИДЙУЛПЧЩНЙ (ТЙУХОПЛ 62, З).
вБОДБЦЙТПЧБООЩЕ ЛПМЕУБ (ТЙУХОПЛ 62, Д), Ч ЛПФПТЩИ УФБМШОПК ВБОДБЦ РПУБЦЕО У ОБФСЗПН ОБ УФБМШОПК (ТЕЦЕ ЮХЗХООЩК) ГЕОФТ, ПВЕУРЕЮЙЧБАФ ЬЛПОПНЙА ЛБЮЕУФЧЕООПК УФБМЙ, ОП ВПМЕЕ ДПТПЗЙ Ч ЙЪЗПФПЧМЕОЙЙ. вБОДБЦ ЛХАФ ЙМЙ РТПЛБФЩЧБАФ. ыЙТПЛЙЕ ЛПМЕУБ (РТЙ ЫЙТЙОЕ ВПМЕЕ 500 НН) ДЕМБАФ У ДЧХНС ВБОДБЦБНЙ. фПМЭЙОБ ВБОДБЦБ ПФ ЧРБДЙОЩ ЪХВШЕЧ (7. 8)m_n.
вПМФПЧЩЕ ЛПОУФТХЛГЙЙ, Ч ЛПФПТЩИ ПВПД Й ГЕОФТ УФСЗЙЧБАФ ЛТЕРЕЦОЩНЙ ВПМФБНЙ, ХУФБОБЧМЙЧБЕНЩНЙ РПД ТБЪЧЕТФЛХ, ЙНЕАФ ФБЛХА ЦЕ ОЕУХЭХА УРПУПВОПУФШ, ЛБЛ Й ВБОДБЦЙТПЧБООЩЕ, ОП МЕЗЮЕ РПУМЕДОЙИ (ТЙУХОПЛ 62,Е). тЙУХОПЛ 62 — лТХРОЩЕ ЪХВЮБФЩЕ ЛПМЕУБ.
уЧБТОЩЕ ЛПМЕУБ РТЙНЕОСА Ч ЙОДЙЧЙДХБМШОПН РТПЙЪЧПДУФЧЕ. пВПД ЧЩРПМОСАФ ГЕМЩН ЙМЙ ЧБМШГПЧБООЩН ЙЪ РПМПУ УП УЧБТЛПК ЧП ЧРБДЙОЕ НЕЦДХ ЪХВШСНЙ (ТЙУХОПЛ 62, Ц).
уЙМЩ, ДЕКУФЧХАЭЙЕ Ч ГЙМЙОДТЙЮЕУЛЙИ РЕТЕДБЮБИ
ъОБОЙЕ ЬФЙИ УЙМ Й ЙИ УПУФБЧМСАЭЙИ РП ПУСН ЛППТДЙОБФ ОЕПВИПДЙНП ДМС ТБУЮЕФБ ЪХВШЕЧ, ЧБМПЧ Й ЙИ ПРПТ. чЩВЙТБЕН УЙУФЕНХ ЛППТДЙОБФ У ОБЮБМПН Ч РПМАУЕ ЪБГЕРМЕОЙС РПУЕТЕДЙОЕ ЫЙТЙОЩ ЧЕОГБ: ПУШ И ОБРТБЧМСЕН ЧДПМШ ПЛТХЦОПК УЛПТПУФЙ, ПУШ Х РЕТРЕОДЙЛХМСТОП Й ПУШ z ЧДПМШ ПУЙ ЪХВЮБФПЗП ЛПМЕУБ (ТЙУХОПЛ 63, Б, В).
тБУУНБФТЙЧБЕН НПНЕОФ ЪБГЕРМЕОЙС Ч РПМАУЕ, УЙМЩ ФТЕОЙС ЧЧЙДХ ЙИ НБМПУФЙ ОЕ ХЮЙФЩЧБАФУС. уЙМЩ ЧЪБЙНПДЕКУФЧЙС ЪХВШЕЧ РТЙ ЬФПН ОБРТБЧМЕОЩ РП МЙОЙЙ ЪБГЕРМЕОЙС.
тБУУНБФТЙЧБЕН УЙМЩ ОБ ДЕМЙФЕМШОЩИ ГЙМЙОДТБИ, ДЕКУФЧХАЭЙЕ Ч ОЕЛПТТЙЗЙТПЧБООЩИ ЪБГЕРМЕОЙСИ ЙМЙ У ЧЩУПФОПК ЛПТТЕЛГЙЕК Й РТЙНЕОСЕНЩЕ ФБЛЦЕ ДМС ТБУЮЕФБ ЧБМПЧ Й РПДЫЙРОЙЛПЧ ЧП ЧУЕИ ЛПТТЙЗЙТПЧБООЩИ ЪБГЕРМЕОЙСИ ЛБЛ МЕЗЛП ПРТЕДЕМСЕНЩЕ Й ПЮЕОШ ВМЙЪЛЙЕ Л УЙМБН ОБ ОБЮБМШОЩИ ГЙМЙОДТБИ.
пЛТХЦОБС УПУФБЧМСАЭБС УЙМЩ (ЧДПМШ ПУЙ И) ДМС ЪХВЮБФЩИ ЛПМЕУ ЧУЕИ ФЙРПЧ:
ЗДЕ ф-РЕТЕДБЧБЕНЩК НПНЕОФ, о·Н;
d— ДЕМЙФЕМШОЩК ДЙБНЕФТ, НН.
РТСНПЪХВЩИ ЛПМЕУ: F_y=F_t tgα _t, F_z=0;
ЛПУПЪХВЩИ ЛПМЕУ F_y=F_t tgα _t, F_z=F_t tgß.
тЙУХОПЛ 63 — уЙМЩ, ДЕКУФЧХАЭЙЕ Ч ЛПУПЪХВПН ГЙМЙОДТЙЮЕУЛПН ЪБГЕРМЕОЙЙ (ДМС РЕТЕДБЮ У ХЗМПЧПК ЛПТТЕЛГЙЕК Х РБТБНЕФТПЧ F_t, α_t , α_n Й ß ДПВБЧМСЕФУС ЙОДЕЛУ w).
оПТНБМШОБС Л РПЧЕТИОПУФЙ ЪХВБ УЙМБ:
РТСНПЪХВЩИ ЛПМЕУ (111)
ЛПУПЪХВЩИ ЛПМЕУ (112)
Cosß _b ВМЙЪПЛ (Й НПЦОП РТЙОЙНБФШ ТБЧОЩН) cosß (sinß _b=sinß cosα _n).
ъХВЮБФЩЕ РЕТЕДБЮЙ НПЗХФ ТБУУЮЙФЩЧБФШУС ОБ ЛПОФБЛФОХА Й ЙЪЗЙВОХА РТПЮОПУФШ РП ТБЪОЩН ЪОБЮЕОЙСН НПНЕОФПЧ TH Й фF, Ч ЮБУФОПУФЙ, ЧУМЕДУФЧЙЕ ТБЪОПЗП ЧМЙСОЙС РЙЛПЧЩИ ОБЗТХЪПЛ ОБ ЛПОФБЛФОХА Й ЙЪЗЙВОХА РТПЮОПУФШ.
тБУЮЕФ ЪХВШЕЧ ГЙМЙОДТЙЮЕУЛЙИ ЪХВЮБФЩИ ЛПМЕУ ОБ ЛПОФБЛФОХА РТПЮОПУФШ
тБУЮЕФ УЧПДЙФУС Л ХДПЧМЕФЧПТЕОЙА ХУМПЧЙС, ЮФПВЩ ЛПОФБЛФОЩЕ ОБРТСЦЕОЙС Ч ЪХВШСИ о ВЩМЙ ТБЧОЩ ЙМЙ НЕОШЫЕ ДПРХУЛБЕНЩИ [σ]_о. тБУЮЕФ ЧЕДХФ ДМС ЪБГЕРМЕОЙС Ч РПМАУЕ, ФБЛ ЛБЛ ЧЩЛТБЫЙЧБОЙЕ ОБЮЙОБЕФУС Х РПМАУОПК МЙОЙЙ (ОБ ОПЦЛЕ), РТЙЮЕН РПМАУОБС МЙОЙС Ч РТСНПЪХВЩИ РЕТЕДБЮБИ ОБИПДЙФУС Ч ЪПОЕ ПДОПРБТОПЗП ЪБГЕРМЕОЙС.
пУОПЧОБС ЖПТНХМБ ДМС ТБУЮЕФБ РТСНПЪХВЩИ РЕТЕДБЮ ОБ ЛПОФБЛФОХА РТПЮОПУФШ:
(113)
ЗДЕ σ_ОП — ОБРТСЦЕОЙЕ РТЙ ОПНЙОБМШОПК ОБЗТХЪЛЕ (л_О=1), РТЕДУФБЧМСАЭЕЕ ЙОФЕТЕУ ДМС ОБЛПРМЕОЙС ПРЩФБ РТПЕЛФЙТПЧБОЙС;
-НОПЦЙФЕМШ, ИБТБЛФЕТЙЪХАЭЙК ХЧЕМЙЮЕОЙЕ ОПНЙОБМШОЩИ ОБРТСЦЕОЙК;
F_t=2·10 3 T_1О/d₁ -ПЛТХЦОБС УЙМБ ОБ ДЕМЙФЕМШОПН ДЙБНЕФТЕ;
ф_1О — ТБУЮЕФОЩК ЧТБЭБАЭЙК НПНЕОФ ОБ ЫЕУФЕТОЕ, о Н;
— ЛПЬЖЖЙГЙЕОФ (ТЙУХОПЛ65), ХЮЙФЩЧБАЭЙК ЖПТНХ УПРТСЦЕООЩИ РПЧЕТИОПУФЕК ЪХВШЕЧ (ПО ПВЯЕДЙОСЕФ НОПЦЙФЕМЙ ЙЪ ЖПТНХМЩ ДМС w_n Й ЙЪ ЖПТНХМЩ ДМС 1/ρ _РТ).
тЙУХОПЛ 64 — уИЕНБ Л ТБУЮЕФХ ЛПОФБЛФОПК РТПЮОПУФЙ ЪХВШЕЧ.
дМС РЕТЕДБЮ ВЕЪ УНЕЭЕОЙС Й РТЙ ЛПЬЖЖЙГЙЕОФБИ УНЕЭЕОЙС И₁+И₂=0 ЛПЬЖЖЙГЙЕОФ Z_H=2,5.
жПТНХМХ ДМС РТПЕЛФОЩИ ТБУЮЕФПЧ, ПРТЕДЕМСАЭХА РТЙВМЙЦЕООП НЕЦПУЕЧПЕ ТБУУФПСОЙЕ a_w ЪХВЮБФЩИ РТСНПЪХВЩИ РЕТЕДБЮ, РПМХЮБАФ ЙЪ ПУОПЧОПК ЪБЧЙУЙНПУФЙ, РПМБЗБС, ЮФП Z_е=190 нрБ 1/2 , Z_ε=0,9, Z_О=2,5, b_w=Ψ_aa_w, d₁≈ d_w1= =2Б_w/(u±1):
(114)
лПУПЪХВЩЕ Й ЫЕЧТПООЩЕ РЕТЕДБЮЙ. ч ФПЮОЩИ ЛПУПЪХВЩИ РЕТЕДБЮБИ Ч УЧСЪЙ У ВПМШЫЙН ПВЭЙН ЛПЬЖЖЙГЙЕОФПН РЕТЕЛТЩФЙС Й МХЮЫЕК РТЙТБВПФЛПК ОБЗТХЪЛБ ТБУРТЕДЕМСЕФУС НЕЦДХ ЪХВШСНЙ ВПМЕЕ ТБЧОПНЕТОП.
пУОПЧОБС ТБУЮЕФОБС ЖПТНХМБ ДМС ЛПУПЪХВЩИ РЕТЕДБЮ РТЙОЙНБЕФ УМЕДХАЭЙК ЧЙД:
(115)
— ЛПЬЖЖЙГЙЕОФ (УН. ТЙУХОПЛ65), ХЮЙФЩЧБАЭЙК ЖПТНХ УПРТСЦЕООЩИ РПЧЕТИОПУФЕК ЪХВШЕЧ (ПО ПВЯЕДЙОСЕФ НОПЦЙФЕМЙ l/cosα_tw ЙЪ ЖПТНХМЩ ДМС w_n Й 2cosß_b/(cosα _t · tgα _tw) ЙЪ ЖПТНХМЩ ДМС l/ РТ) .
— ЛПЬЖЖЙГЙЕОФ, ХЮЙФЩЧБАЭЙК УХННБТОХА ДМЙОХ ЛПОФБЛФОЩИ МЙОЙК (ФПТГПЧЩК ЛПЬЖЖЙГЙЕОФ РЕТЕЛТЩФЙС ε_α ).
рТЙ РТПЕЛФЙТПЧБОЙЙ ОПЧЩИ РЕТЕДБЮ ЙЪ ТБУЮЕФПЧ ОБ ЛПОФБЛФОХА РТПЮОПУФШ ПРТЕДЕМСАФ НЕЦПУЕЧПЕ ТБУУФПСОЙЕ, РТЕДЧБТЙФЕМШОП ЪБДБЧЫЙУШ:
дМС УФБМШОЩИ ЛПМЕУ РПУМЕ РТЕПВТБЪПЧБОЙК Й РПДУФБОПЧЛЙ Ч ПУОПЧОХА ЖПТНХМХ z_E=190 нРБ 1/2 ; z_ε =0,8 (ε_α=l,6); z_H=2,47 (ß =10°, x₁±x₂=0) РПМХЮБЕН:
(117)
тБУЮЕФ ЪХВШЕЧ ГЙМЙОДТЙЮЕУЛЙИ РЕТЕДБЮ ОБ ЙЪЗЙВ
рТСНПЪХВЩЕ РЕТЕДБЮЙ. ъХВ ТБУУНБФТЙЧБЕФУС ЛБЛ ЛПОУПМШОБС ВБМЛБ У ОБЗТХЪЛПК, ТБУРТЕДЕМЕООПК РП МЙОЙЙ ЛПОФБЛФБ. рТЙ ТБВПФЕ МЙОЙС ЛПОФБЛФБ РЕТЕНЕЭБЕФУС РП ЧЩУПФЕ ЪХВБ Й НЕОСЕФУС РМЕЮП УЙМЩ.
рТЙОЙНБЕН, ЮФП УЙМЩ ФТЕОЙС ОБ ЪХВШСИ РТЕОЕВТЕЦЙНП НБМЩ. фПЗДБ НПЦОП УЮЙФБФШ, ЮФП УЙМБ ЧЪБЙНПДЕКУФЧЙС ЪХВШЕЧ ОБРТБЧМЕОБ РП ОПТНБМЙ Л ЛПОФБЛФЙТХАЭЙН РПЧЕТИОПУФСН, Ф. Е. РП МЙОЙЙ ЪБГЕРМЕОЙС ЛБУБФЕМШОПК Л ПУОПЧОЩН ПЛТХЦОПУФСН. уМЕДПЧБФЕМШОП, РТЙ ДЕКУФЧЙЙ РПУФПСООПЗП НПНЕОФБ УЙМБ Ч РТПГЕУУЕ ПДОПРБТОПЗП ЪБГЕРМЕОЙС ПУФБЕФУС РПУФПСООПК.
ч ОБЮБМЕ ТБУУНБФТЙЧБЕН ТБУЮЕФ ДМС УМХЮБС ДЕКУФЧЙС УЙМЩ Ч ЧЕТЫЙОЕ ЪХВБ (ТЙУХОПЛ 65). рТЙОСЧ ТБУЮЕФОХА УЙМХ ТБЧОПК РПМОПК УЙМЕ Ч ЪБГЕРМЕОЙЙ, РПМХЮЙН ХРТПЭЕООЩК ТБУЮЕФ Ч РТЕДРПМПЦЕОЙЙ, ЮФП ЧФПТБС РБТБ ЪХВШЕЧ ОЕ ХЮБУФЧХЕФ Ч ТБВПФЕ (ТБЪОПУФШ ЫБЗПЧ ЪБГЕРМЕОЙС ЪХВШЕЧ ЧУМЕДУФЧЙЕ РПЗТЕЫОПУФЕК ЙЪЗПФПЧМЕОЙС ВПМШЫЕ ХРТХЗПК ДЕЖПТНБГЙЙ ЪХВШЕЧ).
ьФПФ ТБУЮЕФОЩК УМХЮБК РТЙЗПДЕО ДМС ПУОПЧОЩИ ТБУЮЕФПЧ РЕТЕДБЮ ПФОПУЙФЕМШОП ОЕЧЩУПЛПК ФПЮОПУФЙ Й ОБЗТХЦЕООПУФЙ (Ч ЮБУФОПУФЙ, ЙЪ ХМХЮЫЕООЩИ УФБМЕК Й ЮХЗХОБ), ДМС РТЕДЧБТЙФЕМШОЩИ ТБУЮЕФПЧ, ДМС РТПЧЕТПЮОЩИ ТБУЮЕФПЧ У РПМПЦЙФЕМШОЩН ТЕЪХМШФБФПН, РЕТЕДБЮ У РБТБНЕФТБНЙ, ЧЩВТБООЩНЙ РП ДТХЗЙН ЛТЙФЕТЙСН (Ч ЮБУФОПУФЙ, РП ЛТЙФЕТЙА ЛПОФБЛФОПК РТПЮОПУФЙ).
тЙУХОПЛ 65 — уИЕНЩ Л ТБУЮЕФХ ЪХВШЕЧ ОБ ЙЪЗЙВ.
фБЛ ЛБЛ ХУФБМПУФОЩЕ ФТЕЭЙОЩ Й ТБЪТХЫЕОЙЕ ОБЮЙОБАФУС ОБ ТБУФСОХФПК УФПТПОЕ ЪХВБ, ФП ОБ ОЕК Й РТПЧЕТСАФ РТПЮОПУФШ ЪХВШЕЧ. нЕУФОЩЕ ОБРТСЦЕОЙС Ч ПРБУОПН УЕЮЕОЙЙ:
(118)
ЗДЕ -НПНЕОФ УПРТПФЙЧМЕОЙС ОБ ЙЪЗЙВ ПРБУОПЗП УЕЮЕОЙС ЫЙТЙОПК, ТБЧОПК ЕДЙОЙГЕ;
s₁-ФПМЭЙОБ ЪХВБ Ч ПРБУОПН УЕЮЕОЙЙ;
A_s=s₁ — РМПЭБДШ ЕДЙОЙГЩ ДМЙОЩ ПРБУОПЗП УЕЮЕОЙС;
h_p — ТБУЮЕФОПЕ РМЕЮП УЙМЩ;
α_σ — ФЕПТЕФЙЮЕУЛЙК ЛПЬЖЖЙГЙЕОФ ЛПОГЕОФТБГЙЙ ОБРТСЦЕОЙК.
рПДУФБЧЙЧ ЪОБЮЕОЙС w, w_s Й A_s, ЧЩОПУЙН ЪБ УЛПВЛЙ ПВЭЙЕ НОПЦЙФЕМЙ Й ХНОПЦБЕН ЮЙУМЙФЕМШ Й ЪОБНЕОБФЕМШ ОБ m, ФПЗДБ:
(119)
ЗДЕ -ЛПЬЖЖЙГЙЕОФ ЖПТНЩ ЪХВШЕЧ, ЪОБЮЕОЙС ЛПФПТПЗП, Ч ЪБЧЙУЙНПУФЙ ПФ ЮЙУМБ ЪХВШЕЧ Й УНЕЭЕОЙС ЙУИПДОПЗП ЛПОФХТБ И, РПМХЮЕООЩЕ НЕФПДБНЙ ФЕПТЙЙ ХРТХЗПУФЙ, РТЙЧЕДЕОЩ Ч ФБВМЙГЕ 14.
уРЕГЙЖЙЛБ ЧПРТПУПЧ РТПЮОПУФЙ ЛПУПЪХВЩИ Й ЫЕЧТПООЩИ РЕТЕДБЮ Й ПУПВЕООПУФЙ ТБУЮЕФПЧ.
РПОЙЦЕООЩЕ ДЙОБНЙЮЕУЛЙЕ ОБЗТХЪЛЙ Й УППФЧЕФУФЧЕООП ЛПЬЖЖЙГЙЕОФ ДЙОБНЙЮОПУФЙ л_Fv;
МХЮЫБС РТЙТБВПФЛБ Й МХЮЫБС УПЧНЕУФОБС ТБВПФБ РБТ ЪХВШЕЧ, ОБИПДСЭЙИУС Ч ЪБГЕРМЕОЙЙ. ьФП ХЮЙФЩЧБЕФУС ЛПЬЖЖЙГЙЕОФБНЙ Y_ε Й л_Fα. лПЬЖЖЙГЙЕОФ Y_ε=1/ε_α, ХЮЙФЩЧБЕФ ТБУРТЕДЕМЕОЙЕ ОБЗТХЪЛЙ НЕЦДХ ЪХВШСНЙ ЧЩУПЛПФПЮОЩИ ЪХВЮБФЩИ РЕТЕДБЮ, ДМС ЛПФПТЩИ л_Fα=1. чМЙСОЙЕ РПЗТЕЫОПУФЕК ЙЪЗПФПЧМЕОЙС (Ч ПУОПЧОПН ПЫЙВПЛ ЪБГЕРМЕОЙС) ХЮЙФЩЧБАФ ЛПЬЖЖЙГЙЕОФПН л_Fα≥1;
ОБЛМПО ЛПОФБЛФОЩИ МЙОЙК Л ПУОПЧБОЙА ЪХВШЕЧ Й ТБВПФБ ЪХВШЕЧ ЛБЛ РМБУФЙО, Б ОЕ ЛБЛ ВБМПЛ. уППФЧЕФУФЧЕООП ЧЧПДЙФУС ПРЩФОЩК ЛПЬЖЖЙГЙЕОФ:
(120);
ХФПМЭЕОЙЕ ЪХВШЕЧ (ХНЕОШЫЕОЙЕ ЛПЬЖЖЙГЙЕОФПЧ ЖПТНЩ ЪХВШЕЧ). пУОПЧОПЕ ХУМПЧЙЕ ТБУЮЕФБ ОБ ЙЪЗЙВ ЪХВШЕЧ, ЮФПВЩ НЕУФОПЕ ОБРТСЦЕОЙЕ ПФ ЙЪЗЙВБ Ч ПРБУОПН УЕЮЕОЙЙ ВЩМП НЕОШЫЕ ЙМЙ ТБЧОП ДПРХУФЙНПНХ:
(121)
ЗДЕ m — ОПТНБМШОЩК НПДХМШ;
— ПЛТХЦОБС УЙМБ;
T_1F — ТБУЮЕФОЩК ЧТБЭБАЭЙК НПНЕОФ, о·Н;
d₁ — ДЕМЙФЕМШОЩК ДЙБНЕФТ ЫЕУФЕТОЙ, НН;
Y_ß — ЛПЬЖЖЙГЙЕОФ ХЗМБ ОБЛМПОБ ЪХВШЕЧ, ДМС РТСНПЪХВЩИ РЕТЕДБЮ Y_ß=1;
Y_ε=1/ε_α-ЛПЬЖЖЙГЙЕОФ, ХЮЙФЩЧБАЭЙК РЕТЕЛТЩФЙЕ ЪХВШЕЧ.
нЙОЙНБМШОПЕ ЪОБЮЕОЙЕ НПДХМС:
(122)
фБВМЙГБ 14. — лПЬЖЖЙГЙЕОФЩ ЖПТНЩ ЪХВБ.
юЙУМП ЪХВШЕЧ z лПЬЖЖЙГЙЕОФ УНЕЭЕОЙС ЙУИПДОПЗП ЛПОФХТБ x фЕПТЕФЙЮЕУЛЙК ЛПЬЖЖЙГЙЕОФ ЛПОГЕОФТБГЙЙ α₀ РТЙ x=0 (ДМС УРТБЧПЛ)
-0,5 -0,2 0 +0,2 +0,5 +0,8
лПЬЖЖЙГЙЕОФ Y _FS
10 — — — — — 2,96 —
12 — — — — 3,55 3,08 —
14 — — — 4,05 3,56 3,14 —
16 — — 4,47 3,99 3,57 3,17 1,51
17 — — 4,30 3,97 3,58 3,21 1,53
20 — — 4,12 3,90 3,59 3,25 1,62
25 — 4,39 3,96 3,81 3,60 3,33 1,70
30 4,67 4,14 3,85 3,75 3,61 3,37 1,74
40 4,24 3,90 3,75 3,68 3,62 3,44 1,79
50 4,02 3,83 3,73 3,66 3,62 3,48 1,83
60 3,93 3,82 3,73 3,68 3,63 3,52 1,86
80 3,89 3,81 3,74 — — — 1,91
100 3,87 3,80 3,75 — — — 1,94
лПОЙЮЕУЛЙЕ ЪХВЮБФЩЕ ЛПМЕУБ РТЙНЕОСАФ Ч РЕТЕДБЮБИ НЕЦДХ ЧБМБНЙ, ПУЙ ЛПФПТЩИ ТБУРПМПЦЕОЩ РПД ХЗМПН. пУОПЧОПЕ РТЙНЕОЕОЙЕ ЙНЕАФ РЕТЕДБЮЙ У РЕТЕУЕЛБАЭЙНЙУС РПД ХЗМПН 90њ ПУСНЙ, Ф. Е. ПТФПЗПОБМШОЩЕ РЕТЕДБЮЙ, ЛПФПТЩЕ ТБУУНБФТЙЧБАФУС ОЙЦЕ. рЕТЕДБЮЙ У НЕЦПУЕЧЩН ХЗМПН, ОЕ ТБЧОЩН 90њ, РТЙНЕОСАФ ТЕДЛП ЙЪ-ЪБ УМПЦОПУФЙ ЖПТН Й ФЕИОПМПЗЙЙ ЙЪЗПФПЧМЕОЙС ЛПТРХУОЩИ ДЕФБМЕК, ОЕУХЭЙИ ЬФЙ РЕТЕДБЮЙ, ИПФС ДМС ЙЪЗПФПЧМЕОЙС УБНЙИ ЛПМЕУ НЕЦПУЕЧПК ХЗПМ РЕТЕДБЮЙ ОЕ ЙНЕЕФ ЪОБЮЕОЙС.
оЕУНПФТС ОБ ФП, ЮФП ЛПОЙЮЕУЛЙЕ ЛПМЕУБ УМПЦОЕЕ, ЮЕН ГЙМЙОДТЙЮЕУЛЙЕ Ч ЙЪЗПФПЧМЕОЙЙ Й НПОФБЦЕ, ПОЙ ЙНЕАФ ДПУФБФПЮОП ЫЙТПЛПЕ РТЙНЕОЕОЙЕ Ч НБЫЙОПУФТПЕОЙЙ, ПРТЕДЕМСЕНПЕ ХУМПЧЙСНЙ ЛПНРПОПЧЛЙ ХЪМПЧ НБЫЙО.
лПОЙЮЕУЛЙЕ ЛПМЕУБ ЧЩРПМОСАФ У РТСНЩНЙ, ФБОЗЕОГЙБМШОЩНЙ, ЛТХЗПЧЩНЙ Й ДТХЗЙНЙ ЛТЙЧПМЙОЕКОЩНЙ ЪХВШСНЙ (ТЙУХОПЛ 66).
рТСНПЪХВЩЕ ЛПОЙЮЕУЛЙЕ ЛПМЕУБ УМЕДХЕФ РТЙНЕОСФШ РТЙ ОЕЧЩУПЛЙИ ПЛТХЦОЩИ УЛПТПУФСИ (ДП 2. 3 Н/У) ЛБЛ ОБЙВПМЕЕ РТПУФЩЕ Ч НПОФБЦЕ (ДПРХУФЙНП ДП 8 Н/У). рТЙ ВПМЕЕ ЧЩУПЛЙИ УЛПТПУФСИ ГЕМЕУППВТБЪОП РТЙНЕОСФШ ЛПМЕУБ У ЛТХЗПЧЩНЙ ЪХВШСНЙ, ЛБЛ ПВЕУРЕЮЙЧБАЭЙЕ ВПМЕЕ РМБЧОПЕ ЪБГЕРМЕОЙЕ, НЕОШЫЙК ЫХН, ВПМШЫХА ОЕУХЭХА УРПУПВОПУФШ Й ВПМЕЕ ФЕИОПМПЗЙЮОЩЕ.
ъХВШС ПВТБВБФЩЧБАФ ОБ УРЕГЙБМШОЩИ УФБОЛБИ ДМС ОБТЕЪБОЙС ЛПОЙЮЕУЛЙИ ЛПМЕУ.
ч НБУУПЧПН Й ЛТХРОПУЕТЙКОПН РТПЙЪЧПДУФЧЕ Ч УЧСЪЙ У ЧПЪНПЦОПУФША ЛПНРЕОУБГЙЙ РТЙ ОБТЕЪБОЙЙ ЪХВШЕЧ РПУМЕДХАЭЙИ ЪБЛБМПЮОЩИ ДЕЖПТНБГЙК ЛПОЙЮЕУЛЙЕ ЛПМЕУБ ОЕ ЫМЙЖХАФ, Б ПЗТБОЙЮЙЧБАФУС РТЙФЙТЛПК. ч ЛПОЙЮЕУЛЙИ РЕТЕДБЮБИ ДМС ПВЕУРЕЮЕОЙС РТЙ УВПТЛЕ РТБЧЙМШОПЗП ЛПОФБЛФБ ЪХВШЕЧ РТЕДХУНБФТЙЧБАФ ЧПЪНПЦОПУФШ ПУЕЧПК ТЕЗХМЙТПЧЛЙ ЪХВЮБФЩИ ЛПМЕУ.
тЙУХОПЛ 66 — лПОЙЮЕУЛЙЕ ЪХВЮБФЩЕ ЛПМЕУБ:Б — У РТСНЩНЙ; В-У ЛПУЩНЙ; Ч — У ЛТХЗПЧЩНЙ ЪХВШСНЙ.
зЕПНЕФТЙЮЕУЛЙЕ ТБУЮЕФЩ ЛПОЙЮЕУЛЙИ ЪХВЮБФЩИ РЕТЕДБЮ. зЕПНЕФТЙЮЕУЛЙЕ ТБУЮЕФЩ ЛПОЙЮЕУЛЙИ ЛПМЕУ БОБМПЗЙЮОЩ ТБУЮЕФБН ГЙМЙОДТЙЮЕУЛЙИ. ъХВШС ЛПОЙЮЕУЛЙИ ЛПМЕУ ПВТБЪХАФУС ПВЛБФЩЧБОЙЕН РП РМПУЛПНХ ЛПМЕУХ У РТСНПМЙОЕКОЩН РТПЖЙМЕН ЪХВШЕЧ БОБМПЗЙЮОП ФПНХ, ЛБЛ ЪХВШС ГЙМЙОДТЙЮЕУЛЙИ ЛПМЕУ ПВТБЪХАФУС ПВЛБФЩЧБОЙЕН РП ТЕКЛЕ. юЙУМП ЪХВШЕЧ РМПУЛПЗП ЛПМЕУБ (НПЦЕФ РПМХЮЙФШУС ДТПВОЩН). чНЕУФП ОБЮБМШОЩИ Й ДЕМЙФЕМШОЩИ ГЙМЙОДТПЧ ГЙМЙОДТЙЮЕУЛЙИ ЛПМЕУ Ч ЛПОЙЮЕУЛЙИ ЛПМЕУБИ ЧЧПДСФУС РПОСФЙС: ОБЮБМШОЩК Й ДЕМЙФЕМШОЩК ЛПОХУЩ, ЛПФПТЩЕ, ЛБЛ РТБЧЙМП, УПЧРБДБАФ, ФБЛ ЛБЛ ДМС ЛПОЙЮЕУЛЙИ ЛПМЕУ ХЗМПЧХА ЛПТТЕЛГЙА РТБЛФЙЮЕУЛЙ ОЕ РТЙНЕОСАФ. ч ЛБЮЕУФЧЕ ФПТГПЧЩИ УЕЮЕОЙК ТБУУНБФТЙЧБАФ УЕЮЕОЙС РПЧЕТИОПУФСНЙ ДПРПМОЙФЕМШОЩИ ЛПОХУПЧ, Ф. Е. ЛПОХУПЧ, ПУЙ ЛПФПТЩИ УПЧРБДБАФ У ПУША ЛПМЕУБ, Б ПВТБЪХАЭЙЕ РЕТРЕОДЙЛХМСТОЩ Л ПВТБЪХАЭЙН ДЕМЙФЕМШОПЗП ЛПОХУБ (ТЙУХОПЛ 67). йУРПМШЪХАФУС РПОСФЙС ЧОЕЫОЕЗП Й ЧОХФТЕООЕЗП ДПРПМОЙФЕМШОЩИ ЛПОХУПЧ (ПЗТБОЙЮЙЧБАЭЙИ ЪХВЮБФЩК ЧЕОЕГ) Й УТЕДОЕЗП ДПРПМОЙФЕМШОПЗП ЛПОХУБ. дЕКУФЧЙФЕМШОЩЕ РТПЖЙМЙ ЪХВШЕЧ ЛПОЙЮЕУЛЙИ ЛПМЕУ ЧЕУШНБ ВМЙЪЛЙ Л РТПЖЙМСН ЧППВТБЦБЕНЩИ ЬЛЧЙЧБМЕОФОЩИ ГЙМЙОДТЙЮЕУЛЙИ ЛПМЕУ У ТБДЙХУБНЙ ДЕМЙФЕМШОЩИ ПЛТХЦОПУФЕК, ТБЧОЩНЙ ДМЙОБН ПВТБЪХАЭЙИ ДПРПМОЙФЕМШОЩИ ЛПОХУПЧ.
тЙУХОПЛ 67 — уИЕНБ Л ЗЕПНЕФТЙЮЕУЛПНХ ТБУЮЕФХ ЛПОЙЮЕУЛЙИ РЕТЕДБЮ.
ъХВШС ЛПОЙЮЕУЛЙИ ЛПМЕУ РП РТЙЪОБЛХ ЙЪНЕОЕОЙС ТБЪНЕТПЧ УЕЮЕОЙК РП ДМЙОЕ ЧЩРПМОСАФ ФТЕИ ЖПТН:
ПУЕЧБС ЖПТНБ I — ОПТНБМШОП РПОЙЦБАЭЙЕУС ЪХВШС; ЧЕТЫЙОЩ ДЕМЙФЕМШОПЗП Й ЧОХФТЕООЕЗП ЛПОХУПЧ УПЧРБДБАФ (ТЙУХОПЛ 68, Б). ьФХ ЖПТНХ РТЙНЕОСАФ ДМС ЛПОЙЮЕУЛЙИ РЕТЕДБЮ У РТСНЩНЙ Й ФБОЗЕОГЙБМШОЩНЙ ЪХВШСНЙ, Б ФБЛЦЕ ПЗТБОЙЮЕОП ДМС РЕТЕДБЮ У ЛТХЗПЧЩНЙ ЪХВШСНЙ РТЙ m_n≥2 Й z_Σ=20. 100;
ПУЕЧБС ЖПТНБ II — ЧЕТЫЙОБ ЧОХФТЕООЕЗП ЛПОХУБ ТБУРПМБЗБЕФУС ФБЛ, ЮФП ЫЙТЙОБ ДОБ ЧРБДЙОЩ ЛПМЕУБ РПУФПСООБ, Б ФПМЭЙОБ ЪХВБ РП ДЕМЙФЕМШОПНХ ЛПОХУХ ТБУФЕФ У ХЧЕМЙЮЕОЙЕН ТБУУФПСОЙС ПФ ЧЕТЫЙОЩ. ьФБ ЖПТНБ РПЪЧПМСЕФ ПВТБВБФЩЧБФШ ПДОЙН ЙОУФТХНЕОФПН УТБЪХ ПВЕ РПЧЕТИОПУФЙ ЪХВШЕЧ ЛПМЕУБ. рПЬФПНХ ПОБ СЧМСЕФУС ПУОПЧОПК ДМС ЛПМЕУ У ЛТХЗПЧЩНЙ ЪХВШСНЙ, ЫЙТПЛП РТЙНЕОСЕФУС Ч НБУУПЧПН РТПЙЪЧПДУФЧЕ (ТЙУХОПЛ 68, В);
ПУЕЧБС ЖПТНБ III (ТЙУХОПЛ 68, Ч) — ТБЧОПЧЩУПЛЙЕ ЪХВШС; ПВТБЪХАЭЙЕ ДЕМЙФЕМШОПЗП Й ЧОХФТЕООЕЗП ЛПОХУПЧ РБТБММЕМШОЩ. ьФХ ЖПТНХ РТЙНЕОСАФ ДМС ЛТХЗПЧЩИ ЪХВШЕЧ РТЙ z_Σ≥ 40, Ч ЮБУФОПУФЙ РТЙ УТЕДОЙИ ЛПОХУОЩИ ТБУУФПСОЙСИ 75-750 НН.
жПТНЩ II Й III РПМХЮБАФ УНЕЭЕОЙЕН ЧЕТЫЙОЩ ЛПОХУБ ЧРБДЙО Й ЧЕТЫЙОЩ ДЕМЙФЕМШОПЗП ЛПОХУБ (ТЙУХОПЛ 68,В, Ч).
х ЛПОЙЮЕУЛЙИ ЛПМЕУ ХДПВОП ЙЪНЕТСФШ, Б РПФПНХ Й ЪБДБЧБФШ ТБЪНЕТЩ ЪХВШЕЧ ОБ ЧОЕЫОЕН ДПРПМОЙФЕМШОПН ЛПОХУЕ. ч ЪХВЮБФЩИ ЛПМЕУБИ У ЪХВШСНЙ ЖПТНЩ I ПВЩЮОП ПРЕТЙТХАФ ПЛТХЦОЩН НПДХМЕН mtЕ ОБ ЧОЕЫОЕН ФПТГЕ. ч ЪХВЮБФЩИ ЛПМЕУБИ У ЪХВШСНЙ ЖПТНЩ II Й III РТЕЙНХЭЕУФЧЕООП ПРЕТЙТХАФ ОПТНБМШОЩН НПДХМЕН m_nm ОБ УЕТЕДЙОЕ ЫЙТЙОЩ ЪХВЮБФПЗП ЧЕОГБ.
тЙУХОПЛ 68 — жПТНЩ ЪХВШЕЧ ЛПОЙЮЕУЛЙИ РЕТЕДБЮ.
лТХЗПЧЩЕ ЪХВШС ОБТЕЪБАФ ОЕНПДХМШОЩН ЙОУФТХНЕОФПН, РПЪЧПМСАЭЙН ПВТБВБФЩЧБФШ ЪХВШС Ч ОЕЛПФПТПН ДЙБРБЪПОЕ НПДХМЕК. рПЬФПНХ ДПРХУЛБЕФУС РТЙНЕОСФШ РЕТЕДБЮЙ У ОЕУФБОДБТФОЩНЙ Й ДТПВОЩНЙ НПДХМСНЙ. уППФОПЫЕОЙЕ НЕЦДХ НПДХМСНЙ m_tЕ Й m_nm УМЕДХАЭЕЕ:
(123)
ЗДЕ R_Е — ЧОЕЫОЕЕ ЛПОХУОПЕ ТБУУФПСОЙЕ (УН. ТЙУХОПЛ 67).
хЗПМ ОБЛМПОБ МЙОЙЙ ЪХВБ ЧЩВЙТБАФ, ХЮЙФЩЧБС, ЮФП ХЧЕМЙЮЕОЙЕ ß_m ХМХЮЫБЕФ РМБЧОПУФШ ЪБГЕРМЕОЙС, ОП РТЙ ЬФПН ЧПЪТБУФБАФ ХУЙМЙС. рТЙ ЛТХЗПЧЩИ ЪХВШСИ РТЕЙНХЭЕУФЧЕООП РТЙНЕОСАФ ß_m=35њ, Б РТЙ ФБОЗЕОГЙБМШОЩИ 20. 30њ, ПВЩЮОП ХЗПМ ß_m ЧЩВЙТБАФ ЛТБФОЩН 5њ.
нЙОЙНБМШОП ДПРХУФЙНЩЕ ЮЙУМБ ЪХВШЕЧ РТЙЧЕДЕОЩ Ч ФБВМЙГЕ 15. дМС ХНЕОШЫЕОЙС ЫХНБ ТЕЛПНЕОДХАФ РТЙНЕОСФШ РТЙФЙТЛХ Й ЧЩВЙТБФШ ОЕЛТБФОЩЕ ЮЙУМБ ЪХВШЕЧ ЛПМЕУ.
дМС ЪХВЮБФЩИ РЕТЕДБЮ У ФЧЕТДПУФША ТБВПЮЙИ РПЧЕТИОПУФЕК ЪХВШЕЧ ЫЕУФЕТОЙ о₁ Й ЛПМЕУБ о₂≥ 45оRу_Ь ЮЙУМП ЪХВШЕЧ ЫЕУФЕТОЙ ТЕЛПНЕОДХАФ ЧЩВЙТБФШ РП ТЙУХОЛХ 69 Ч ЪБЧЙУЙНПУФЙ ПФ ЧОЕЫОЕЗП ДЕМЙФЕМШОПЗП ДЙБНЕФТБ ЫЕУФЕТОЙ d_e1, РТЙ ФЧЕТДПУФЙ о₁ Й H₂≤ 350оч ЧЩВТБООЩЕ ЪОБЮЕОЙС z₁ ХЧЕМЙЮЙЧБАФ Ч 1,6 ТБЪБ; РТЙ H₁≥ 45 оRу_Ь Й H₂≤ 350 оч z₁ ХЧЕМЙЮЙЧБАФ Ч 1,3 ТБЪБ.
фБВМЙГБ 15. — нЙОЙНБМШОП ДПРХУФЙНЩЕ ЮЙУМБ ЪХВШЕЧ ЫЕУФЕТОЙ
рЕТЕДБФПЮОПЕ ЮЙУМП u z₁ РТЙ ß·m
0:15 20:25 30:40
1 17 17 17
1,6 15 15 14
2 13 12 11
≥3,15 12 10 8
тЙУХОПЛ 69 — зТБЖЙЛ ДМС ПРТЕДЕМЕОЙС ЮЙУЕМ ЪХВШЕЧ ЫЕУФЕТОЙ: Б — РТСНПЪХВПК; В- У ЛТХЗПЧЩНЙ ЪХВШСНЙ.
пУОПЧОЩЕ ЗЕПНЕФТЙЮЕУЛЙЕ УППФОПЫЕОЙС Ч ЛПОЙЮЕУЛЙИ РЕТЕДБЮБИ РТЙЧЕДЕОЩ Ч ФБВМЙГБИ 16. 18.
фБВМЙГБ 16. — пУОПЧОЩЕ ТБЪНЕТЩ ЛПОЙЮЕУЛЙИ ЛПМЕУ; У ТБЧОПЧЩУПЛЙНЙ ЪХВШСНЙ (ПУЕЧБС ЖПТНБ ЪХВШЕЧ III)
рБТБНЕФТ ЪБГЕРМЕОЙС жПТНХМБ
чЩУПФБ ЪХВБ
чЩУПФБ ЗПМПЧЛЙ ЪХВБ h=2h * _am_nm+c, ЗДЕ h*_a=1; c=0,25m_nm
h_{a 1}=m_nm(h * _a+x₁); h_{a 2}=2h * _a m_nm— h_{a 1}
хЗПМ ОБЮБМШОПЗП, ОБТХЦОПЗП Й ЧОХФТЕООЕЗП ЛПОХУПЧ tgδ₁=z₁/ z₂; δ₂=90°-δ₁
пЛТХЦОБС ФПМЭЙОБ ЪХВБ Ч УТЕДОЕН ОПТНБМШОПН УЕЮЕОЙЙ S_n1=(0,5π+2x₁tgα_0n+x_τ)m_nm; S_n1=πm_nm-S_n1
рТЙНЕЮБОЙЕ. чЕМЙЮЙОЩ Й ПРТЕДЕМСАФУС ФБЛ ЦЕ, ЛБЛ Й РТЙ ПУЕЧПК ЖПТНЕ ЪХВБ I.
фБВМЙГБ 17. — пУОПЧОЩЕ ТБЪНЕТЩ ЛПОЙЮЕУЛЙИ ЪХВЮБФЩИ ЛПМЕУ У РТСНЩНЙ, ФБОЗЕОГЙБМШОЩНЙ Й ЛТХЗПЧЩНЙ РПОЙЦБАЭЙНЙУС ЪХВШСНЙ (ПУЕЧБС ЖПТНБ ЪХВШЕЧ I) РТЙ НЕЦПУЕЧПН ХЗМЕ Σ =90њ
рБТБНЕФТ ЪБГЕРМЕОЙС жПТНХМБ
чОЕЫОЕЕ ЛПОХУОПЕ ТБУУФПСОЙЕ R_e=0,5m_tez_Σ
ыЙТЙОБ ЧЕОГБ b≤0,3R,sub>e(k_be=b/R_e≤0,3)
уТЕДОЕЕ ЛПОХУОПЕ ТБУУФПСОЙЕ R_m=R,sub>e-0,5b
оБЙВПМШЫБС ЧЩУПФБ
ЪХВШЕЧ (Х ФПТГБ) h_e=2h * _tem_te+c, ЗДЕ h * _te=cosß_m; c=0,2m_te
ЗПМПЧЛЙ ЪХВШЕЧ (Х ФПТГБ) h_ae1=(h * _te+x₁ cosß_m) m_te; h_ae2=2h * _tem_te— h_ae1
ОПЦЛЙ ЪХВШЕЧ h_fe1= h_e— h_ae1; h_fe2= h_e— h_ae2
пЛТХЦОБС ФПМЭЙОБ ЪХВБ РП ЧОЕЫОЕК ДЕМЙФЕМШОПК ПЛТХЦОПУФЙ S_e1=(0,5π+2x₁tgα_n+x_τ)m_te; S_e1=π m_te— S_e1
хЗПМ:
ОПЦЛЙ ЪХВШЕЧ tgθ_t1=h_fe1/R_e; tgθ_f2=h_fe1/R_e;
ДЕМЙФЕМШОПЗП (ОБЮБМШОПЗП) ЛПОХУБ tgδ₁=z₁/z₂; tgδ₂=90°- δ
ЛПОХУБ ЧЕТЫЙО δ_a1=δ₁+θ_f2;δ_a2=δ₂+θ_f1
ЛПОХУБ ЧРБДЙО δ_f1=δ₁+θ_f1; δ_f2=δ₂+θ_f2
дЙБНЕФТ
чОЕЫОЕК ДЕМЙФЕМШОПК ПЛТХЦОПУФЙ d_e1=m_tez₁; d_e2=m_tez₂
чОЕЫОЙК ЧЕТЫЙО d_ae1= d_e1+2h_ae1cosδ₁; d_ae2= d_e2+2h_ae2cosδ₂;
тБУЮЕФОПЕ ВБЪПЧПЕ ТБУУФПСОЙЕ (ПФ ЧЕТЫЙОЩ ДЕМЙФЕМШОПЗП ЛПОХУБ ДП ПУОПЧБОЙС ОБТХЦОПЗП ЛПОХУБ) A₁=R_ecosδ₁— h_ae1sinδ₁; A₂=R_ecosδ₂— h_ae2sinδ₂;
ьЛУГЕОФТЙУЙФЕФ ДМС ФБОЗЕОГЙБМШОЩИ ЪХВШЕЧ e=R_msinß_m
хЗПМ ОБЛМПОБ
ФБОЗЕОГЙБМШОЩИ ЪХВШЕЧ Х ФПТГБ ЛТХЗПЧЩИ ЪХВШЕЧ sinß_e=e/R_e ß_e=ß_m+∆ß, ЗДЕ ∆=b(C_A-C_B/R_m; C_A=57,3/d_ЙОcosß_m; C_B=28,65tgß_m; d_ЙО=(1,7÷2,1)R_m
* пВПЪОБЮБЕФ ЧЕМЙЮЙОХ Ч ДПМСИ НПДХМС.
фБВМЙГБ 18. — пУОПЧОЩЕ ТБЪНЕТЩ ЛПОЙЮЕУЛЙИ ЪХВЮБФЩИ ЛПМЕУ У РПУФПСООПК ЫЙТЙОПК ДОБ ЧРБДЙОЩ (ПУЕЧБС ЖПТНБ ЪХВШЕЧ II)
рБТБНЕФТ ЪБГЕРМЕОЙС жПТНХМБ
уТЕДОЕЕ ЛПОХУОПЕ ТБУУФПСОЙЕ R_m=m_nmz_Σ/2cosß_m
ыЙТЙОБ ЪХВЮБФПЗП ЧЕОГБ b≤0,35R_m(k_bm=b/R_m≤0,35)
чОЕЫОСС ЛПОХУОБС ДЙУФБОГЙС R_e=R_m+0,5b
чЩУПФБ ЗПМПЧЛЙ ЪХВБ РПУТЕДЙОЕ ЫЙТЙОЩ ЧЕОГБ h_a1=(h * _a+x₁)m_nm; h_a2=2h * _a m_nm— h_a1; ЗДЕ h * _a=1
пЛТХЦОБС ФПМЭЙОБ ЪХВБ Ч УТЕДОЕН ОПТНБМШОПН УЕЮЕОЙЙ s_nm1=(0,5π+2x₁tgα_n+x_τ1)m_nm; s_nm2=πm_nm— s_nm1
рТПНЕЦХФПЮОБС ТБУЮЕФОБС ЧЕМЙЮЙОБ (ПРТЕДЕМСЕФУС РТЙ ß≠0 Й ПЛТХЗМСЕФУС ДП ГЕМПЗП ЮЙУМБ, ЛТБФОПЗП 10)
d_ЙО=(1,5:2,3)R_m
уХННБ ХЗМПЧ ОПЦЕЛ ЪХВШЕЧ ЫЕУФЕТОЙ Й ЛПМЕУБ Ч НЙОХФХ рТЙ ß_m≠0 θ_fΣ=a cosecß_m; РТЙ ß=0
хЗПМ ОПЦЛЙ ЪХВБ (ПЛТХЗМЙФШ ДП 1) θ_f2=θ_fΣ-θ_f1
рПРТБЧЛБ ЧЩУПФЩ ЗПМПЧЛЙ РТЙ РЕТЕИПДЕ ОБ ЧОЕЫОЙК ЛПОХУ ∆h_a1=0,5b tgθ_f2; ∆h_a1=0,5b tgθ_f2
оБЙВПМШЫБС ЧЩУПФБ:
ЗПМПЧЛЙ ЪХВШЕЧ (РП ФПТГХ) h_{ae 1}= h_a1+∆h_a1; h_{ae 2}= h_a2+∆h_a2
ЪХВБ РП ФПТГХ h_e= 2h_a+c+∆h_a1+∆h_a1
рТЙНЕЮБОЙЕ. чЕМЙЮЙОЩ δ, δ_a, δ_f, δ_e, δ_ae, A ПРТЕДЕМСАФ ФБЛ ЦЕ, ЛБЛ РТЙ ЖПТНЕ ЪХВБ I
тБУЮЕФЩ ЛПОЙЮЕУЛЙИ ЪХВЮБФЩИ ЛПМЕУ ОБ РТПЮОПУФШ
тБУЮЕФЩ УФТПСФ ЛБЛ ТБУЮЕФЩ ЬЛЧЙЧБМЕОФОЩИ ГЙМЙОДТЙЮЕУЛЙИ ЛПМЕУ.
рПФЕТЙ НПЭОПУФЙ Ч ЪХВЮБФЩИ РЕТЕДБЮБИ Ч ПУОПЧОПН УЛМБДЩЧБАФУС ЙЪ РПФЕТШ:
ОБ ФТЕОЙЕ Ч ЪБГЕРМЕОЙЙ;
ОБ ТБЪВТЩЪЗЙЧБОЙЕ НБУМБ;
Ч РПДЫЙРОЙЛБИ.
Ч ПУПВП ВЩУФТПИПДОЩИ РЕТЕДБЮБИ НПЗХФ ВЩФШ ЪОБЮЙФЕМШОЩНЙ ЧЕОФЙМСГЙПООЩЕ РПФЕТЙ.
ЗДЕ Ψ _Ъ,Ψ_Т,Ψ_Р — ПФОПУЙФЕМШОЩЕ РПФЕТЙ Ч ЪБГЕРМЕОЙЙ, ОБ ТБЪВТЩЪЗЙЧБОЙЕ НБУМБ Й Ч РПДЫЙРОЙЛБИ.
рПФЕТЙ Ч ЪБГЕРМЕОЙЙ ЧЩЪЩЧБАФУС УЙМБНЙ ФТЕОЙС НЕЦДХ ЪХВШСНЙ. уЙМЩ ФТЕОЙС Ч ТЕЦЙНЕ РПМХЦЙДЛПУФОПК УНБЪЛЙ ТБУФХФ У ХЧЕМЙЮЕОЙЕН ЫЕТПИПЧБФПУФЙ РПЧЕТИОПУФЙ, У ХНЕОШЫЕОЙЕН ЧСЪЛПУФЙ НБУМБ Й У ХНЕОШЫЕОЙЕН УЛПТПУФЙ. чМЙСОЙЕ ЬФЙИ ЖБЛФПТПЧ ОБ УЙМХ ФТЕОЙС Ч ЪОБЮЙФЕМШОПК УФЕРЕОЙ УЧСЪБОП У ЙИ ЧМЙСОЙЕН ОБ ОЕУХЭХА УРПУПВОПУФШ НБУМСОПЗП ЛМЙОБ НЕЦДХ ЪХВШСНЙ.
рТЙ ВПМШЫЙИ УЛПТПУФСИ ЧУФХРБАФ Ч УЙМХ ЪБЧЙУЙНПУФЙ, ИБТБЛФЕТОЩЕ ДМС ЗЙДТПДЙОБНЙЮЕУЛПК УНБЪЛЙ.
рПФЕТЙ ОБ ФТЕОЙЕ Ч ЪБГЕРМЕОЙЙ ПВЩЮОП РТЙОЙНБАФ РТПРПТГЙПОБМШОЩНЙ РПМЕЪОПК ОБЗТХЪЛЕ Й ПФОПУСФ Л ФБЛ ОБЪЩЧБЕНЩН ОБЗТХЪПЮОЩН РПФЕТСН. лПЬЖЖЙГЙЕОФ ФТЕОЙС УЛПМШЦЕОЙС НЕЦДХ ЪХВШСНЙ f Ч ЪБЧЙУЙНПУФЙ ПФ ХЛБЪБООЩИ ЖБЛФПТПЧ ПВЩЮОП ЛПМЕВМЕФУС Ч РТЕДЕМБИ 0,025. 0,08. ъБ ТБУЮЕФОЩЕ НПЦОП РТЙОЙНБФШ УМЕДХАЭЙЕ ЕЗП ЪОБЮЕОЙС Ч ЪБЧЙУЙНПУФЙ ПФ УХННБТОПК УЛПТПУФЙ ЛБЮЕОЙС Й v_Σ =2v_ПЛТsinα _t .
v_Σ, Н/У 1 10 20 30 60
f 0,08 0,06 0,05 0,04 0,025
пФОПУЙФЕМШОЩЕ РПФЕТЙ Ч ЪБГЕРМЕОЙЙ РТСНПЪХВЩИ Й ЛПУПЪХВЩИ РЕТЕДБЮ ЧЩЮЙУМСАФ ЛБЛ ПФОПЫЕОЙЕ ТБВПФЩ УЙМ ФТЕОЙС УЛПМШЦЕОЙС НЕЦДХ ЪХВШСНЙ РТЙ РПЧПТПФЕ ЛПМЕУ ОБ ПДЙО ЫБЗ Л РЕТЕДБЧБЕНПК ЛПМЕУБНЙ РПМЕЪОПК ТБВПФЕ ЪБ ФПФ ЦЕ РЕТЙПД:
(125)
ЗДЕ k_Ψ — ЛПЬЖЖЙГЙЕОФ, ТБЧОЩК ДМС:
ОЕЛПТТЙЗЙТПЧБООПЗП ЪБГЕРМЕОЙС 1;
ДМС ЪБГЕРМЕОЙС У ЧЩУПФОПК ЛПТТЕЛГЙЕК РТЙ И=0,5 k_Ψ =1,15; РТЙ И=0,8 k_Ψ=1,4, ЪОБЛ «+» ДМС ЧОЕЫОЕЗП, «-» ДМС ЧОХФТЕООЕЗП ЪБГЕРМЕОЙС.
жПТНХМБ РПЛБЪЩЧБЕФ, ЮФП РПФЕТЙ УЙМШОП ХЧЕМЙЮЙЧБАФУС У ХНЕОШЫЕОЙЕН ЮЙУЕМ ЪХВШЕЧ, ПУПВЕООП ЫЕУФЕТОЙ.
рПФЕТЙ ОБ ТБЪНЕЫЙЧБОЙЕ Й ТБЪВТЩЪЗЙЧБОЙЕ НБУМБ ТБУФХФ У ХЧЕМЙЮЕОЙЕН ЧСЪЛПУФЙ НБУМБ, ПЛТХЦОПК УЛПТПУФЙ, ЫЙТЙОЩ ЛПМЕУ, ЗМХВЙОЩ РПЗТХЦЕОЙС. ч ПФМЙЮЙЕ ПФ РПФЕТШ ОБ ФТЕОЙЕ Ч ЪБГЕРМЕОЙЙ ПОЙ ОЕ ЪБЧЙУСФ ПФ ОБЗТХЪЛЙ Й РПЬФПНХ ПФОПУСФУС Л ЮЙУМХ РПУФПСООЩИ РПФЕТШ.
пФОПУЙФЕМШОЩЕ РПФЕТЙ ОБ ТБЪНЕЫЙЧБОЙЕ Й ТБЪВТЩЪЗЙЧБОЙЕ НБУМБ ДМС ЛПМЕУБ, РПЗТХЦЕООПЗП Ч НБУМП ОБ ЗМХВЙОХ, ТБЧОХА ПДЙОБТОПК ЙМЙ ДЧПКОПК ЧЩУПФЕ ЪХВБ, НПЗХФ ВЩФШ РТЙВМЙЦЕООП ПРТЕДЕМЕОЩ РП УМЕДХАЭЙН ЖПТНХМБН:
(126)
(127)
ЗДЕ F_Т — ПЛТХЦОБС УЙМБ, ЪБФТБЮЙЧБЕНБС ОБ ТБЪНЕЫЙЧБОЙЕ Й ТБЪВТЩЪЗЙЧБОЙЕ НБУМБ, о;
v — ПЛТХЦОБС УЛПТПУФШ, Н/У;
b — ЫЙТЙОБ ЛПМЕУ, НН;
— ДЙОБНЙЮЕУЛБС ЧСЪЛПУФШ НБУМБ РТЙ ТБВПЮЕК ФЕНРЕТБФХТЕ, рБ·У;
У-ЛПЬЖЖЙГЙЕОФ, ТБЧОЩК 30 (РТЙ УФТХКОПК УНБЪЛЕ У =20).
уТЕДОЙЕ ЪОБЮЕОЙС лрд ЪХВЮБФЩИ РЕТЕДБЮ ОБ РПДЫЙРОЙЛБИ ЛБЮЕОЙС РТЙ ЙУРПМШЪПЧБОЙЙ РПМОПК ТБУЮЕФОПК НПЭОПУФЙ РТЙЧЕДЕОЩ Ч ФБВМЙГЕ 19.
рТЙ РЕТЕДБЮЕ ОЕРПМОПК НПЭОПУФЙ лрд ЪОБЮЙФЕМШОП ОЙЦЕ ЧУМЕДУФЧЙЕ ЧМЙСОЙС РПУФПСООЩИ РПФЕТШ, Ф. Е. РПФЕТШ, ОЕ ЪБЧЙУСЭЙИ ПФ РЕТЕДБЧБЕНПК НПЭОПУФЙ.
фБВМЙГБ 19. — уТЕДОЙЕ ЪОБЮЕОЙС лрд ЪХВЮБФЩИ РЕТЕДБЮ ОБ РПДЫЙРОЙЛБИ ЛБЮЕОЙС
лПОУФТХЛГЙС рЕТЕДБЮБ
ГЙМЙОДТЙЮЕУЛБС ЛПОЙЮЕУЛБС
ъБЛТЩФБС УТЕДОЕУЛПТПУФОБС У ЦЙДЛПК УНБЪЛПК 0,98 0,97
ъБЛТЩФБС ЧЩУПЛПК ФПЮОПУФЙ У ЦЙДЛПК УНБЪЛПК ВЩУФТПИПДОБС 0,99 0,98
пФЛТЩФБС У РМБУФЙЮОПК УНБЪЛПК 0,96 0,95
ьЧПМШЧЕОФОБС УЙУФЕНБ ЪБГЕРМЕОЙС, РПМХЮЙЧЫБС Ч ФЕИОЙЛЕ ЧЧЙДХ УЧПЙИ ВЕУУРПТОЩИ ДПУФПЙОУФЧ ЫЙТПЮБКЫЕЕ ТБУРТПУФТБОЕОЙЕ, ЙНЕЕФ, ПДОБЛП, ОЕЛПФПТЩЕ ОЕДПУФБФЛЙ:
НБМЩЕ РТЙЧЕДЕООЩЕ ТБДЙХУЩ ЛТЙЧЙЪОЩ ТБВПЮЙИ РПЧЕТИОПУФЕК;
РПЧЩЫЕООХА Ч УЧСЪЙ У МЙОЕКОЩН ЛПОФБЛФПН ЪХВШЕЧ ЮХЧУФЧЙФЕМШОПУФШ Л РЕТЕЛПУБН;
РПФЕТЙ ОБ ФТЕОЙЕ Ч ЪБГЕРМЕОЙЙ Ч УЧСЪЙ У УХЭЕУФЧЕООЩН УЛПМШЦЕОЙЕН.
ьФЙ ОЕДПУФБФЛЙ ХНЕОШЫЕОЩ Ч ЪБГЕРМЕОЙЙ оПЧЙЛПЧБ.
ч ЬФПН ЪБГЕРМЕОЙЙ (ТЙУХОПЛ 70) ЛПОФБЛФ ЪХВШЕЧ РЕТЕНЕЭБЕФУС ОЕ РП РТПЖЙМА, ЛБЛ Ч РТСНПЪХВПН ЬЧПМШЧЕОФОПН ЪБГЕРМЕОЙЙ, Б ЧДПМШ ЪХВБ, РТЙЮЕН УЛПТПУФШ РЕТЕНЕЭЕОЙС Й ХЗПМ ДБЧМЕОЙС ПУФБАФУС РПУФПСООЩНЙ.
тЙУХОПЛ 70 — гЙМЙОДТЙЮЕУЛБС РЕТЕДБЮБ оПЧЙЛПЧБ пмъ.
ьФП РПЪЧПМСЕФ ПЮЕТЮЙЧБФШ РТПЖЙМЙ ЪХВШЕЧ ОЕУПРТСЦЕООЩНЙ ЛТЙЧЩНЙ, Ч ЮБУФОПУФЙ ДХЗБНЙ ПЛТХЦОПУФЕК У ВМЙЪЛЙНЙ ТБДЙХУБНЙ ЛТЙЧЙЪОЩ РТЙ ЧОХФТЕООЕН ЛБУБОЙЙ. мЙОЙС ЪБГЕРМЕОЙС ТБУРПМПЦЕОБ РБТБММЕМШОП ПУСН ЛПМЕУ, Б ОЕ Ч РМПУЛПУФЙ ЙИ ЧТБЭЕОЙС.
оЕПВИПДЙНЩН ХУМПЧЙЕН ОЕРТЕТЩЧОПУФЙ ЪБГЕРМЕОЙС ЪХВШЕЧ Й РПУФПСОУФЧБ НЗОПЧЕООПЗП РЕТЕДБФПЮОПЗП ПФОПЫЕОЙС СЧМСЕФУС ХУМПЧЙЕ, ЮФПВЩ ЛПЬЖЖЙГЙЕОФ РЕТЕЛТЩФЙС ВЩМ ВПМШЫЕ ЕДЙОЙГЩ. ч ЛПУПЪХВЩИ ЬЧПМШЧЕОФОЩИ РЕТЕДБЮБИ ПО УЛМБДЩЧБЕФУС ЙЪ ФПТГПЧПЗП Й ПУЕЧПЗП ЛПЬЖЖЙГЙЕОФПЧ РЕТЕЛТЩФЙС. ч РЕТЕДБЮЕ оПЧЙЛПЧБ ФПТГПЧЩК ЛПЬЖЖЙГЙЕОФ РЕТЕЛТЩФЙС ТБЧЕО ОХМА. уМЕДПЧБФЕМШОП, ПУЕЧПК ЛПЬЖЖЙГЙЕОФ РЕТЕЛТЩФЙС ДПМЦЕО ВЩФШ ВПМШЫЕ ЕДЙОЙГЩ, Й ЛПМЕУБ ПВСЪБФЕМШОП ДПМЦОЩ ЙНЕФШ ОЕРТСНЩЕ ЪХВШС. бЛФЙЧОЩЕ РПЧЕТИОПУФЙ ЪХВШЕЧ РТЕДУФБЧМСАФ УПВПК ФТХВЮБФЩЕ ЛТХЗПЧЙОФПЧЩЕ РПЧЕТИОПУФЙ, РПЬФПНХ РЕТЕДБЮЙ оПЧЙЛПЧБ НПЦОП ОБЪЩЧБФШ ЛТХЗПЧЙОФПЧЩНЙ РЕТЕДБЮБНЙ.
ч РТПДПМШОПК РМПУЛПУФЙ Ч УЧСЪЙ У ВПМШЫЙНЙ ТБДЙХУБНЙ ЛТЙЧЙЪОЩ БЛФЙЧОЩИ РПЧЕТИОПУФЕК ЛБУБОЙЕ РТПЙУИПДЙФ ФБЛЦЕ У ВПМШЫЙН РТЙЧЕДЕООЩН ТБДЙХУПН ЛТЙЧЙЪОЩ. фБЛЙН ПВТБЪПН, ДБЧМЕОЙЕ ТБУРТПУФТБОСЕФУС ОБ ЪОБЮЙФЕМШОХА РМПЭБДШ ЛПОФБЛФБ.
рЕТЕДБЮЙ оПЧЙЛПЧБ ПВМБДБАФ РПЧЩЫЕООПК ЛПОФБЛФОПК ОЕУХЭЕК УРПУПВОПУФША РП УТБЧОЕОЙА У ЬЧПМШЧЕОФОЩНЙ Ч 1,5. 2 ТБЪБ. ьФП ЧЩЪЧБОП, ЧП-РЕТЧЩИ, ЛБУБОЙЕН ЧЩРХЛМПК РПЧЕТИОПУФЙ РП ЧПЗОХФПК Й УППФЧЕФУФЧЕООП ВПМШЫПК РМПЭБДЛПК ЛПОФБЛФБ Й, ЧП-ЧФПТЩИ, РПЧЩЫЕООПК ХДЕМШОПК ОЕУХЭЕК уРПУПВОПУФША НБУМСОПЗП ЛМЙОБ НЕЦДХ ЪХВШСНЙ. рПУМЕДОЕЕ УЧСЪБОП У ФЕН, ЮФП УЛПТПУФШ ЛБЮЕОЙС ОБРТБЧМЕОБ РЕТРЕОДЙЛХМСТОП Л МЙОЙЙ ЛПОФБЛФБ Й Ч ОЕУЛПМШЛП ТБЪ РТЕЧЩЫБЕФ ФБЛПЧХА Ч ЬЧПМШЧЕОФОЩИ РЕТЕДБЮБИ.
рЕТЕДБЮЙ оПЧЙЛПЧБ РПМХЮЙМЙ ТБУРТПУФТБОЕОЙЕ Ч тПУУЙЙ Й ЪБ ТХВЕЦПН Ч ТЕДХЛФПТБИ ПВЭЕЗП ОБЪОБЮЕОЙС, Ч УХДПУФТПЕОЙЙ Й ТСДЕ ДТХЗЙИ ПФТБУМЕК НБЫЙОПУФТПЕОЙС. ч РМБОЕФБТОЩИ РЕТЕДБЮБИ Й ЛПТПВЛБИ РЕТЕДБЮ (УЛПТПУФЕК) ЧУМЕДУФЧЙЕ ВПМШЫЕК ЫЙТЙОЩ, ЮЕН Ч РТСНПЪХВЩИ ЬЧПМШЧЕОФОЩИ, ЙИ РТЙНЕОЕОЙЕ ЪБФТХДОЕОП.
ч УЧСЪЙ У ГЙЛМЙЮЕУЛЙН ЙЪНЕОЕОЙЕН ПРПТОЩИ ТЕБЛГЙК Ч ПВЩЮОЩИ ЛПУПЪХВЩИ РЕТЕДБЮБИ оПЧЙЛПЧБ УМЕДХЕФ УЮЙФБФШ РЕТУРЕЛФЙЧОЩНЙ ДМС ВЩУФТПИПДОЩИ НПЭОЩИ НБЫЙО ЫЕЧТПООЩЕ РЕТЕДБЮЙ оПЧЙЛПЧБ ЙМЙ РЕТЕДБЮЙ оПЧЙЛПЧБ У БТПЮОЩН ЪХВПН, ПВЕУРЕЮЙЧБАЭЙЕ РПУФПСОУФЧП ТЕБЛГЙК.
рТЙНЕОЕОЙЕ РЕТЕДБЮ оПЧЙЛПЧБ ОБЮБМПУШ У РЕТЕДБЮ У ПДОПК МЙОЙЕК ЪБГЕРМЕОЙС (пмъ), Б Ч ОБУФПСЭЕЕ ЧТЕНС Ч ПУОПЧОПН РТЙНЕОСАФ РЕТЕДБЮЙ У ДЧХНС МЙОЙСНЙ ЪБГЕРМЕОЙС (дмъ), ЛПФПТЩЕ ТБУУНБФТЙЧБАФУС ОЙЦЕ.
ч РЕТЕДБЮБИ У ПДОПК МЙОЙЕК ЪБГЕРМЕОЙС РТПЖЙМШ ЪХВБ ПДОПЗП ЛПМЕУБ (ЛБЛ РТБЧЙМП, ЫЕУФЕТОЙ) ДЕМБЕФУС ЧЩРХЛМЩН (УН. ТЙУХОПЛ 70), Б ДТХЗПЗП — ЧПЗОХФЩН.
еУМЙ ЧЕДХЭЙН СЧМСЕФУС ЪХВЮБФПЕ ЛПМЕУП У ЧЩРХЛМЩН РТПЖЙМЕН ЪХВШЕЧ, ФП ФПЮЛБ ЛПОФБЛФБ ТБУРПМПЦЕОБ ЪБ РПМАУПН Й РЕТЕДБЮХ ОБЪЩЧБАФ ЪБРПМАУОПК. еУМЙ ЧЕДЕФ ЛПМЕУП У ЧПЗОХФЩН РТПЖЙМЕН, ФП РЕТЕДБЮБ УФБОПЧЙФУС ДПРПМАУОПК.
чЩРХЛМЩК РТПЖЙМШ ТБУРПМБЗБЕФУС ЧОЕ ОБЮБМШОПК ПЛТХЦОПУФЙ, ЮФП РПЪЧПМСЕФ ДЕМБФШ ЫЕУФЕТОА ВЕЪ ЧТЕЪБОЙС Ч ЧБМ РТЙ ЪОБЮЙФЕМШОП НЕОШЫЕН ЮЙУМЕ ЪХВШЕЧ, ЮЕН РТЙ ЬЧПМШЧЕОФОПН РТПЖЙМЕ. тБДЙХУЩ ЛТЙЧЙЪОЩ РТПЖЙМЕК ЧЩВЙТБАФ ЧЕУШНБ ВМЙЪЛЙНЙ РП БВУПМАФОПК ЧЕМЙЮЙОЕ. ч ТЕЪХМШФБФЕ РТЙТБВПФЛЙ ПВЕУРЕЮЙЧБЕФУС ЛБУБОЙЕ РП ЧЩУПФЕ ЪХВШЕЧ, ВМЙЪЛПЕ Л МЙОЕКЮБФПНХ.
рЕТЕДБЮХ У ДЧХНС МЙОЙСНЙ ЪБГЕРМЕОЙС НПЦОП РТЕДУФБЧЙФШ ЛБЛ УПЮЕФБОЙЕ ДПРПМАУОПК Й ЪБРПМАУОПК РЕТЕДБЮЙ. зПМПЧЛЙ ЪХВШЕЧ ЫЕУФЕТОЙ Й ЛПМЕУБ ЙНЕАФ ЧЩРХЛМЩК РТПЖЙМШ, Б ОПЦЛЙ — ЧПЗОХФЩК.
дМС ОБТЕЪБОЙС ЧЩРХЛМЩИ Й ЧПЗОХФЩИ ЪХВШЕЧ ФТЕВХАФУС ТБЪОЩЕ ЙОУФТХНЕОФЩ. ъХВШС РЕТЕДБЮ У ДЧХНС МЙОЙСНЙ ЪБГЕРМЕОЙС ОБТЕЪБАФ ПДОЙН ЙОУФТХНЕОФПН. ьФЙ РЕТЕДБЮЙ ПВМБДБАФ ВПМШЫЕК ЛПОФБЛФОПК Й ЙЪЗЙВОПК РТПЮОПУФША.
йУИПДОЩК ЛПОФХТ Ч ОПТНБМШОПН УЕЮЕОЙЙ РЕТЕДБЮ У ПДОПК МЙОЙЕК ЪБГЕРМЕОЙС У ФЧЕТДПУФША ЪХВШЕЧ ДП 320 оч (ТЙУХОПЛ 71) ХУФБОПЧМЕО ОПТНБМША но 4229-63. хЗПМ ДБЧМЕОЙС РТЙОСФ ТБЧОЩН 30°, ЗМХВЙОБ ЪБИПДБ ЪХВШЕЧ 1,15 Ф, УППФОПЫЕОЙЕ ТБДЙХУПЧ ЛТЙЧЙЪОЩ РТПЖЙМЕК ρ _f ≈ 1,1ρ _Б.
пУОПЧОПЕ РТЙНЕОЕОЙЕ Ч ОБУФПСЭЕЕ ЧТЕНС РПМХЮЙМЙ РЕТЕДБЮЙ оПЧЙЛПЧБ дмъ У ЙУИПДОЩН ЛПОФХТПН РП зпуф 15023-76 Й РЕТУРЕЛФЙЧОЩНЙ ЛПОФХТБНЙ дмъ 1,0-0,15 Й дмъ 0,7-0,15.
лПОФХТ РП зпуф 15023-76 (ТЙУХОПЛ 72) ТБУРТПУФТБОСЕФУС ОБ РЕТЕДБЮЙ ФЧЕТДПУФША ≤320оч У m≤16 НН Й v≤20 Н/У. вПМЕЕ ЧЩУПЛЙЕ РПЛБЪБФЕМЙ ПВЕУРЕЮЙЧБАФ ЛПОФХТЩ дмъ 1,0-0,15 Й дмъ 0,7-0,15.
лПОФХТ дмъ 1,0-0,15 (ТЙУХОПЛ 73) У ТБДЙХУБНЙ РТПЖЙМЕК Ч ДПМСИ ПФ ОПТНБМШОПЗП НПДХМС 1,0 Й 1,15 РТЙНЕОСАФ РТЙ ФЧЕТДПУФЙ ЪХВШЕЧ ≤40оRу_Ь.
лПОФХТ дмъ 0,7-0,15 (ТЙУХОПЛ 74) У ТБДЙХУБНЙ РТПЖЙМЕК 0,7 Й 0,85 РТЙНЕОСАФ РТЙ ФЧЕТДПУФЙ ≥45оRу_Ь. рЕТЕДБЮЙ У ЛПОФХТПН дмъ 1,0-0,15 РТПЧЕТЕОЩ Ч ЬЛУРМХБФБГЙЙ РТЙ v ДП 98 Н/У.
тЙУХОПЛ 71 — йУИПДОЩК ЛПОФХТ, ОПТНБМШ но 4229-63. тЙУХОПЛ 72 — йУИПДОЩК ЛПОФХТ РП зпуф 15023-76.
нПДХМШ m тЙУХОПЛ 73 — йУИПДОЩК ЛПОФХТ дмъ 1,0-0,15. тЙУХОПЛ 74 — йУИПДОЩК ЛПОФХТ дмъ 0,7-0,15.
ч РПУМЕДОЙЕ ЗПДЩ РПМХЮБАФ ТБУРТПУФТБОЕОЙЕ ГЙМЙОДТЙЮЕУЛЙЕ РЕТЕДБЮЙ У БТПЮОЩНЙ ЪХВШСНЙ (БТПЮОЩЕ). бТПЮОЩЕ РЕТЕДБЮЙ ЧЕУШНБ РЕТУРЕЛФЙЧОЩ ВМБЗПДБТС УХЭЕУФЧЕООЩН РТЕЙНХЭЕУФЧБН: НБМПК ЮХЧУФЧЙФЕМШОПУФЙ Л РЕТЕЛПУХ ПУЕК Й РПЧЩЫЕООПК РТПЮОПУФЙ ЪХВШЕЧ ОБ ЙЪЗЙВ.
бТПЮОЩЕ ЪХВШС ОБТЕЪБАФ ТЕЪГПЧЩНЙ ЗПМПЧЛБНЙ НЕФПДБНЙ РЕТЙПДЙЮЕУЛПЗП ЙМЙ ОЕРТЕТЩЧОПЗП ДЕМЕОЙС. ч РЕТЧПН УМХЮБЕ МЙОЙС ЪХВБ РТЕДУФБЧМСЕФ УПВПК ДХЗХ ПЛТХЦОПУФЙ, ЧП ЧФПТПН — ДХЗХ ХДМЙОЕООПК ГЙЛМПЙДЩ. рТЙ ЬФПН ДПУФБФПЮОПК ДМС РТБЛФЙЮЕУЛЙИ ТБУЮЕФПЧ ФПЮОПУФША РТПЖЙМШ БТПЮОПЗП ЪХВБ Ч УТЕДОЕН ФПТГПЧПН УЕЮЕОЙЙ УППФЧЕФУФЧХЕФ РТПЖЙМА РТСНПЗП ЬЧПМШЧЕОФОПЗП ЪХВБ.
жПТНБ БТПЮОПЗП ЪХВБ ИБТБЛФЕТЙЪХЕФУС УМЕДХАЭЙНЙ ДЧХНС ЗЕПНЕФТЙЮЕУЛЙНЙ РБТБНЕФТБНЙ:
ЛПЬЖЖЙГЙЕОФПН ДМЙОЩ ЪХВБ Ψ _m=b_w/m
ЛПЬЖЖЙГЙЕОФПН ЛТХФЙЪОЩ БТЛЙ ЪХВБ Ψ _R=b_w/R, ЗДЕ R — ХУФБОПЧПЮОЩК ТБДЙХУ ТЕЪГБ ОБ ТЕЪГПЧПК ЗПМПЧЛЕ, b_w — ЫЙТЙОБ ЪХВЮБФПЗП ЧЕОГБ.
пВЩЮОП РТЙОЙНБАФ Ψ_m =10. 20, Ψ_R =1,1. 1,3.
дМС ТБУЮЕФБ ОБ РТПЮОПУФШ ЛПМЕУП У БТПЮОЩНЙ ЪХВШСНЙ ЪБНЕОСАФ ЬЛЧЙЧБМЕОФОЩН ЛПМЕУПН У ЫЕЧТПООЩНЙ ЪХВШСНЙ У ФБЛЙНЙ ЦЕ ДЙБНЕФТПН ОБЮБМШОПК ПЛТХЦОПУФЙ, ЮЙУМПН ЪХВШЕЧ Й НПДХМЕН. хЗПМ ОБЛМПОБ ЬЛЧЙЧБМЕОФОПЗП РПМХЫЕЧТПОБ ДМС ХЛБЪБООПЗП ДЙБРБЪПОБ ЪОБЮЕОЙК R УППФЧЕФУФЧЕООП ТБЧЕО 16. 20њ.
ъХВЮБФЩЕ ТЕДХЛФПТЩ — ЬФП НЕИБОЙЪНЩ, УМХЦБЭЙЕ ДМС РПОЙЦЕОЙС ХЗМПЧЩИ УЛПТПУФЕК Й ХЧЕМЙЮЕОЙС ЛТХФСЭЙИ НПНЕОФПЧ Й ЧЩРПМОСЕНЩЕ Ч ЧЙДЕ ПФДЕМШОЩИ БЗТЕЗБФПЧ. ъХВЮБФЩЕ ТЕДХЛФПТЩ ЙНЕАФ ЫЙТПЛПЕ РТЙНЕОЕОЙЕ, ПУПВЕООП Ч РПДЯЕНОП-ФТБОУРПТФОПН, НЕФБММХТЗЙЮЕУЛПН, ИЙНЙЮЕУЛПН НБЫЙОПУФТПЕОЙЙ, Ч УХДПУФТПЕОЙЙ Й Ф. Д.
рТЙ НБМЩИ ПВЭЙИ РЕТЕДБФПЮОЩИ ПФОПЫЕОЙСИ РТЙНЕОСАФ ПДОПУФХРЕОЮБФЩЕ ТЕДХЛФПТЩ (ТЙУХОПЛ 75,Б). рЕТЕДБФПЮОЩЕ ЮЙУМБ ГЕМЕУППВТБЪОП ЧЩВЙТБФШ ОЕ ВПМШЫЕ 6,3 (РТЕДРПЮФЙФЕМШОП ДП 5) ЧП ЙЪВЕЦБОЙЕ ХЧЕМЙЮЕОЙС ЗБВБТЙФПЧ.
тЙУХОПЛ 75 — оБЙВПМЕЕ ТБУРТПУФТБОЕООЩЕ УИЕНЩ ТЕДХЛФПТПЧ.
оБЙВПМШЫЕЕ ТБУРТПУФТБОЕОЙЕ Ч ОБУФПСЭЕЕ ЧТЕНС ЙНЕАФ ДЧХИУФХРЕОЮБФЩЕ ТЕДХЛФПТЩ (ТЙУХОПЛ 75,В, Ч, З). дМС ОЙИ ОБЙВПМЕЕ ИБТБЛФЕТОЩ РЕТЕДБФПЮОЩЕ ПФОПЫЕОЙС 6,3. 40 (50).
рТЙ РЕТЕДБФПЮОЩИ ПФОПЫЕОЙСИ 25. 250 РТЙНЕОСАФ ФТЕИУФХРЕОЮБФЩЕ ТЕДХЛФПТЩ (ТЙУХОПЛ 75, Д, Е). йИ ПВМБУФШ РТЙНЕОЕОЙС ТБУЫЙТСЕФУС ЪБ УЮЕФ ДЧХИУФХРЕОЮБФЩИ ТЕДХЛФПТПЧ У ВПМШЫЙНЙ РЕТЕДБФПЮОЩНЙ ПФОПЫЕОЙСНЙ, ОП ПДОПЧТЕНЕООП ЙИ, ЕУФЕУФЧЕООП, ВХДХФ ЮБУФЙЮОП ЪБНЕОСФШ ВПМЕЕ ЛПНРБЛФОЩНЙ РМБОЕФБТОЩНЙ Й ЧПМОПЧЩНЙ ТЕДХЛФПТБНЙ.
нЕЦПУЕЧЩЕ ТБУУФПСОЙС ТЕДХЛФПТПЧ ОБЪОБЮБАФ ЙЪ ТСДБ R20.
рЕТЕДБФПЮОЩЕ ПФОПЫЕОЙС ТЕДХЛФПТПЧ ЧЩВЙТБАФ РП ОПТНБМШОПНХ ТСДХ ЮЙУЕМ ЪОБНЕОБФЕМЕН 1,25 (1-К РТЕДРПЮФЙФЕМШОЩК ТСД) ЙМЙ УП ЪОБНЕОБФЕМЕН 1,12 (2-К ТСД).
йЪ ДЧХИУФХРЕОЮБФЩИ ТЕДХЛФПТПЧ ОБЙВПМШЫЕЕ ТБУРТПУФТБОЕОЙЕ ЙНЕАФ ТЕДХЛФПТЩ РП ТБЪЧЕТОХФПК УИЕНЕ (ТЙУХОПЛ 75,В). ьФЙ ТЕДХЛФПТЩ ОБЙВПМЕЕ РТПУФЩ. пОЙ ЙНЕАФ ОБЙНЕОШЫХА ЫЙТЙОХ, ОП ОЕУЙННЕФТЙЮОПЕ ТБУРПМПЦЕОЙЕ ЛПМЕУ ОБ ЧБМБИ РТЙЧПДЙФ Л РПЧЩЫЕООПК ЛПОГЕОФТБГЙЙ ОБЗТХЪЛЙ ДМЙОЕ ЪХВБ. рПЬФПНХ ФБЛЙЕ ТЕДХЛФПТЩ ФТЕВХАФ ЦЕУФЛЙИ ЧБМПЧ. хЛБЪБООЩК ОЕДПУФБФПЛ ВПМШЫЕ УЛБЪЩЧБЕФУС РТЙ ЪБЛБМЕООЩИ ДП ЧЩУПЛПК ФЧЕТДПУФЙ ЛПМЕУБИ Й ОЕТБЧОПНЕТОПК ОБЗТХЪЛЕ (РТЙТБВПФЛБ ЪБФТХДОЕОБ).
ч ГЕМСИ ХМХЮЫЕОЙС ХУМПЧЙК ТБВПФЩ ОБЙВПМЕЕ ОБЗТХЦЕООПК ФЙИПИПДОПК УФХРЕОЙ РТЙНЕОСАФ ТЕДХЛФПТЩ У ТБЪДЧПЕООПК ВЩУФТПИПДОПК УФХРЕОША (ТЙУХОПЛ 75, З). дМС ПВЕУРЕЮЕОЙС ТБЧОПНЕТОПК ОБЗТХЪЛЙ — ПВЕЙИ ЪХВЮБФЩИ РБТ ВЩУФТПИПДОПК УФХРЕОЙ ЙИ ДЕМБАФ ЛПУПЪХВЩНЙ. РТЙЮЕН ПДОХ РБТХ — РТБЧПК, Б ДТХЗХА — МЕЧПК, Й ПДЙО ЧБМ ХУФБОБЧМЙЧБАФ ОБ РПДЫЙРОЙЛБИ, ДПРХУЛБАЭЙИ ПУЕЧХА УБНПХУФБОПЧЛХ. дЕЖПТНБГЙЙ ЧБМПЧ ФЙИПИПДОПК УФХРЕОЙ ОЕ ЧЩЪЩЧБАФ ЛБЛПК-МЙВП УХЭЕУФЧЕООПК ЛПОГЕОФТБГЙЙ ОБЗТХЪЛЙ РП ДМЙОЕ ЪХВШЕЧ ЧУМЕДУФЧЙЕ УЙННЕФТЙЮОПЗП ТБУРПМПЦЕОЙС ЛПМЕУ. тЕДХЛФПТЩ РПМХЮБАФУС ОБ 20 % МЕЗЮЕ ТЕДХЛФПТПЧ РП ТБЪЧЕТОХФПК УИЕНЕ.
пФОПЫЕОЙЕ НЕЦПУЕЧЩИ ТБУУФПСОЙК ФЙИПИПДОПК Й ВЩУФТПИПДОПК УФХРЕОЙ ДЧХИУФХРЕОЮБФЩИ ТЕДХЛФПТПЧ Б_wф/Б_wв =1,12. 1,6. вПМШЫЕЕ ЪОБЮЕОЙЕ ПРФЙНБМШОП РТЙ ВПМШЫЙИ РЕТЕДБФПЮОЩИ ПФОПЫЕОЙСИ Й РПУФПСООПН ТЕЦЙНЕ ОБЗТХЪЛЙ, ч УППФЧЕФУФЧЙЙ У РТЕЙНХЭЕУФЧЕООЩНЙ ХУМПЧЙСНЙ ЙУРПМШЪПЧБОЙС ТЕДХЛФПТПЧ ГЕМЕУППВТБЪОБ ФЕОДЕОГЙС ХНЕОШЫЕОЙС ЬФПЗП ПФОПЫЕОЙС. фБЛ, ДМС ЛТБОПЧЩИ ТЕДХЛФПТПЧ ТЕЛПНЕОДХАФ 1,25.
уППУОЩЕ ТЕДХЛФПТЩ (ТЙУХОПЛ 75, Ч) ЙНЕАФ НБМЩЕ ЗБВБТЙФЩ РП ДМЙОЕ. йИ РТЙНЕОЕОЙЕ УМЕДХЕФ ТБУЫЙТСФШ.
фТЕИУФХРЕОЮБФЩЕ ТЕДХЛФПТЩ ЧЩРПМОСАФ РП ТБЪЧЕТОХФПК УИЕНЕ (ТЙУХОПЛ 75,Д), БОБМПЗЙЮОПК УИЕНЕ, РПЛБЪБООПК ОБ ТЙУХОЛЕ 75, В, ЙМЙ РП УИЕНЕ (ТЙУХОПЛ 75, Е) У ТБЪДЧПЕООПК РТПНЕЦХФПЮОПК УФХРЕОША. ч РПУМЕДОЙИ ПВЕУРЕЮЙЧБАФУС ВМБЗПРТЙСФОЩЕ ХУМПЧЙС ДМС ТБВПФЩ ВЩУФТПИПДОПК Й ФЙИПИПДОПК УФХРЕОЕК.
рТЙ ОЕПВИПДЙНПУФЙ ЧЪБЙНОПК РЕТРЕОДЙЛХМСТОПУФЙ ЧИПДОПЗП Й ЧЩИПДОПЗП ЧБМПЧ Й ОЕВПМШЫПН РЕТЕДБФПЮОПН ПФОПЫЕОЙЙ РТЙНЕОСАФ ЛПОЙЮЕУЛЙЕ ТЕДХЛФПТЩ (ТЙУХОПЛ 75, Ц), Б РТЙ ВПМШЫЙИ РЕТЕДБФПЮОЩИ ПФОПЫЕОЙСИ — ЛПНВЙОЙТПЧБООЩЕ ЛПОЙЮЕУЛП-ГЙМЙОДТЙЮЕУЛЙЕ ТЕДХЛФПТЩ (ТЙУХОПЛ 75,Ъ). вЩУФТПИПДОПК ДЕМБАФ ЛПОЙЮЕУЛХА РЕТЕДБЮХ.
пВЭЕЕ РЕТЕДБФПЮОПЕ ПФОПЫЕОЙЕ ДЧХИ- Й НОПЗПУФХРЕОЮБФЩИ ТЕДХЛФПТПЧ ТБЪВЙЧБАФ НЕЦДХ УФХРЕОСНЙ Ч УППФЧЕФУФЧЙЙ У ЪБДБООЩНЙ ХУМПЧЙСНЙ ПРФЙНЙЪБГЙЙ. пУОПЧОЩН ХУМПЧЙЕН ДМС ТЕДХЛФПТПЧ ПВЭЕЗП ОБЪОБЮЕОЙС СЧМСЕФУС НЙОЙНХН НБУУЩ Й УППФЧЕФУФЧЕООП НЙОЙНХН ПВЯЕНБ. дМС ДЧХИУФХРЕОЮБФЩИ ОЕУППУОЩИ ТЕДХЛФПТПЧ ЧЩЗПДОП ПВЕУРЕЮЙЧБФШ ТБЧЕОУФЧП ДЙБНЕФТПЧ ЛПМЕУ ВЩУФТПИПДОПК Й ФЙИПИПДОПК УФХРЕОЙ. уППФЧЕФУФЧЕООП РЕТЕДБФПЮОПЕ ЮЙУМП ВЩУФТПИПДОПК УФХРЕОЙ u_в=(0,75. 1), ЗДЕ ЛПЬЖЖЙГЙЕОФ 0,75 РТЙОЙНБАФ РТЙ РЕТЕНЕООПН ТЕЦЙНЕ (ЛПЬЖЖЙГЙЕОФ ДПМЗПЧЕЮОПУФЙ T Ч о·Н. еЗП ЧЕМЙЮЙОБ Ч ОБЙВПМШЫЕК УФЕРЕОЙ ЪБЧЙУЙФ ПФ ФЧЕТДПУФЙ ЪХВЮБФЩИ ЛПМЕУ. х ТЕДХЛФПТПЧ ПУОПЧОЩИ ФЙРПЧ У ГЕНЕОФПЧБООЩНЙ Й ЪБЛБМЕООЩНЙ ЪХВШСНЙ γ= 0,03. 0,05 Й ЙНЕЕФ ФЕОДЕОГЙА Л УОЙЦЕОЙА.
ч РЕТЕДБЮБИ У РЕТЕУЕЛБАЭЙНЙУС ПУСНЙ (ЛПОЙЮЕУЛЙНЙ ЛПМЕУБНЙ) ПДОП ЙЪ ЛПМЕУ, ЛБЛ РТБЧЙМП, РТЙИПДЙФУС ХУФБОБЧМЙЧБФШ ЛПОУПМШОП, ЮФП ХИХДЫБЕФ ХУМПЧЙС ТБВПФЩ РЕТЕДБЮЙ.
ч РЕТЕДБЮБИ У РЕТЕЛТЕЭЙЧБАЭЙНЙУС ПУСНЙ ПВБ ЧБМБ НПЦОП ЧЩЧЕУФЙ ЪБ РТЕДЕМЩ РЕТЕДБЮЙ Ч ПВПЙИ ОБРТБЧМЕОЙСИ. ьФП НПЦЕФ РТЕДУФБЧЙФШ УХЭЕУФЧЕООЩЕ РТЕЙНХЭЕУФЧБ РТЙ ОЕПВИПДЙНПУФЙ РТЙЧПДЙФШ ПФ ПДОПЗП ЧБМБ ОЕУЛПМШЛП ДТХЗЙИ. дМС РЕТЕДБЮ У РЕТЕЛТЕЭЙЧБАЭЙНЙУС ПУСНЙ ИБТБЛФЕТОБ РМБЧОПУФШ ТБВПФЩ. оП Ч ОЙИ ЙНЕАФ НЕУФП РПЧЩЫЕООЩЕ УЛПТПУФЙ УЛПМШЦЕОЙС, ЙЪОБЫЙЧБОЙС Й РПФЕТЙ ОБ ФТЕОЙЕ.
чЙОФПЧЩЕ ЪХВЮБФЩЕ РЕТЕДБЮЙ.
чЙОФПЧЩНЙ ОБЪЩЧБАФУС РЕТЕДБЮЙ, УПУФПСЭЙЕ ЙЪ ЛПУПЪХВЩИ ГЙМЙОДТЙЮЕУЛЙИ ЛПМЕУ У РЕТЕЛТЕЭЙЧБАЭЙНЙУС ПУСНЙ (ТЙУХОПЛ 76).
тЙУХОПЛ 76 — чЙОФПЧБС ЪХВЮБФБС РЕТЕДБЮБ Й УИЕНБ ЧЙОФПЧПК ЪХВЮБФПК РЕТЕДБЮЙ.
ч ЧЙОФПЧЩИ РЕТЕДБЮБИ ОБЮБМШОПЕ ЛБУБОЙЕ НЕЦДХ ЪХВШСНЙ РТПЙУИПДЙФ Ч ФПЮЛЕ Ч ХУМПЧЙСИ ЪОБЮЙФЕМШОЩИ УЛПТПУФЕК УЛПМШЦЕОЙС. рПЬФПНХ ОЕУХЭБС УРПУПВОПУФШ ЬФЙИ РЕТЕДБЮ ОЕЧЕМЙЛБ, Й ПОЙ РТЙ ЪОБЮЙФЕМШОЩИ ОБЗТХЪЛБИ ХУФХРБАФ НЕУФП ЗЙРПЙДОЩН Й НОПЗПЪБИПДОЩН ЮЕТЧСЮОЩН.
пУОПЧОПЕ РТЙНЕОЕОЙЕ ЙНЕАФ ЧЙОФПЧЩЕ РЕТЕДБЮЙ У НЕЦПУЕЧЩН ХЗМПН, ТБЧОЩН 90њ.
зЙРПЙДОЩЕ ЙМЙ ЛПОЙЮЕУЛЙЕ ЧЙОФПЧЩЕ РЕТЕДБЮЙ ПУХЭЕУФЧМСАФУС ЛПОЙЮЕУЛЙНЙ ЛПМЕУБНЙ У РЕТЕЛТЕЭЙЧБАЭЙНЙУС ПУСНЙ (ТЙУХОПЛ 77). зЙРПЙДОЩЕ ЛПМЕУБ, ЛБЛ РТБЧЙМП, ЧЩРПМОСАФ У ЛТХЗПЧЩНЙ ЪХВШСНЙ. рЕТЕДБФПЮОЩЕ ЮЙУМБ ПВЩЮОП ЧЩВЙТБАФ Ч ДЙБРБЪПОЕ ПФ 1 ДП 10, Ч РТЕДЕМЕ ДП 60. дПРПМОЙФЕМШОП Л ХЛБЪБООЩН ПВЭЙН ДПУФПЙОУФЧБН РЕТЕДБЮ ЪБГЕРМЕОЙЕН У РЕТЕЛТЕЭЙЧБАЭЙНЙУС ПУСНЙ (РМБЧОПУФШ ТБВПФЩ, ЧПЪНПЦОПУФШ ЧЩЧПДЙФШ ЧБМЩ ЪБ РТЕДЕМЩ РЕТЕДБЮЙ Ч ПВЕ УФПТПОЩ) ЗЙРПЙДОЩЕ РЕТЕДБЮЙ ПВМБДБАФ РПЧЩЫЕООПК ОЕУХЭЕК УРПУПВОПУФША. ьФП РТЕЦДЕ ЧУЕЗП УЧСЪБОП У ФЕН, ЮФП Ч ЗЙРПЙДОЩИ РЕТЕДБЮБИ ПФМЙЮЙЕ ПФ ЧЙОФПЧЩИ ПВЕУРЕЮЙЧБЕФУС ЛПОФБЛФ, ВМЙЪЛЙК Л МЙОЕКОПНХ, У ПРФЙНБМШОЩНЙ ЖПТНПК Й ТБЪНЕТБНЙ РСФОБ ЛПОФБЛФБ.
ч ЬФПН ПФОПЫЕОЙЙ ПОЙ БОБМПЗЙЮОЩ ЛПОЙЮЕУЛЙН РЕТЕДБЮБН У ЛТЙЧПМЙОЕКОЩНЙ ЪХВШСНЙ. уЛПТПУФЙ УЛПМШЦЕОЙС Ч ЗЙРПЙДОЩИ РЕТЕДБЮБИ ЪОБЮЙФЕМШОП НЕОШЫЕ, ЮЕН Ч ЧЙОФПЧЩИ. рТЙ ФПН ЦЕ ДЙБНЕФТЕ ЛПМЕУБ Й РЕТЕДБФПЮОПН ЮЙУМЕ ДЙБНЕФТ ЫЕУФЕТОЙ Ч ЗЙРПЙДОЩИ РЕТЕДБЮБИ РПМХЮБЕФУС ВПМШЫЕ, ЮЕН ЛПОЙЮЕУЛЙИ.
тЙУХОПЛ 77 — зЙРПЙДОБС РЕТЕДБЮБ.
лТПНЕ ФПЗП, ЪХВШС Ч ЗЙРПЙДОЩИ РЕТЕДБЮБИ ИПТПЫП РТЙФЙТБАФУС Й ОЕ РПДЧЕТЦЕОЩ УХЭЕУФЧЕООЩН ЙУЛБЦЕОЙСН ЧУМЕДУФЧЙЕ ДПУФБФПЮОП ТБЧОПНЕТОПЗП УЛПМШЦЕОЙС РП ТБВПЮЕК РПЧЕТИОПУФЙ ЪХВШЕЧ. вМБЗПДБТС ФПНХ, ЮФП Ч ЪБГЕРМЕОЙЙ ПДОПЧТЕНЕООП ОБИПДЙФУС ОЕУЛПМШЛП РБТ ЪХВШЕЧ, ЗЙРПЙДОЩЕ РЕТЕДБЮЙ НПЗХФ РТЙНЕОСФШУС Ч НЕИБОЙЪНБИ ЧЩУПЛПК ФПЮОПУФЙ, Ч ЮБУФОПУФЙ Ч ЛБЮЕУФЧЕ ДЕМЙФЕМШОЩИ РЕТЕДБЮ РТЕГЙЪЙПООЩИ ЪХВПТЕЪОЩИ УФБОЛПЧ. ъОБЮЙФЕМШОПЕ ТБУРТПУФТБОЕОЙЕ ЗЙРПЙДОЩЕ РЕТЕДБЮЙ РПМХЮЙМЙ Ч БЧФПНПВЙМСИ Й ДТХЗЙИ ФТБОУРПТФОЩИ НБЫЙОБИ, Ч ВХНБЗПДЕМБФЕМШОЩИ, Ч ФЕЛУФЙМШОЩИ Й ДТХЗЙИ НБЫЙОБИ. ч ФЕЛУФЙМШОЩИ НБЫЙОБИ ЗЙРПЙДОЩЕ РЕТЕДБЮЙ ДЕМБАФ ЧПЪНПЦОЩН РТЙЧПД ПФ ПДОПЗП ЧБМБ ДП 200 ЧЕТЕФЕО.
оЕДПУФБФЛПН ЗЙРПЙДОЩИ РЕТЕДБЮ СЧМСЕФУС РПЧЩЫЕООБС ПРБУОПУФШ ЪБЕДБОЙК, УЧСЪБООБС У ОБМЙЮЙЕН УЛПМШЦЕОЙС ЧДПМШ ЛПОФБЛФОЩИ МЙОЙК. уТЕДУФЧПН РПЧЩЫЕОЙС УПРТПФЙЧМЕОЙС ЪБЕДБОЙА ЗЙРПЙДОЩИ РЕТЕДБЮ УМХЦЙФ РТЙНЕОЕОЙЕ РТПФЙЧПЪБДЙТОЩИ УНБЪПЮОЩИ НБФЕТЙБМПЧ, ЛПФПТЩЕ ВЩМЙ ЧРЕТЧЩЕ ТБЪТБВПФБОЩ РТЙНЕОЙФЕМШОП Л ЗЙРПЙДОЩН РЕТЕДБЮБН.
пРБУОПУФШ ЪБЕДБОЙК ФЕН НЕОШЫЕ, ЮЕН НЕОШЫЕ ЗЙРПЙДОПЕ УНЕЭЕОЙЕ, Ф. Е. НЕЦПУЕЧПЕ ТБУУФПСОЙЕ е (УН. ТЙУХОПЛ 77).
рТЙ РТПЕЛФЙТПЧБОЙЙ ЗЙРПЙДОЩИ РЕТЕДБЮ ПВЩЮОП ЧЩВЙТБАФ ЗЙРПЙДОПЕ УНЕЭЕОЙЕ е=(0,2. 0,3)d_БЕ2; Ч РЕТЕДБЮБИ МЕЗЛПЧЩИ БЧФПНПВЙМЕК Й МЕЗЛЙИ ЗТХЪПЧЙЛПЧ е≤0,2m_tЕ·z_У, Б Ч РЕТЕДБЮБИ ФСЦЕМЩИ ФТБОУРПТФОЩИ НБЫЙО е≤0,1m_tЕ·z_У, ЗДЕ:
(128)
хЗМЩ ОБЛМПОБ ЪХВШЕЧ ЫЕУФЕТОЙ У ЕЕ ПУША ПВЩЮОП ЧЩВЙТБАФ ß₁=50· ЙМЙ ОЕУЛПМШЛП ХНЕОШЫБАФ У ХЧЕМЙЮЕОЙЕН ЮЙУМБ ЪХВШЕЧ:
рТЙ ЬФПН ХЗМЩ ОБЛМПОБ ЪХВШЕЧ ЛПМЕУБ ß₂=30. 35њ (УДЧЙЗ ФПТГПЧ ЪХВШЕЧ ЛПМЕУБ ДПМЦЕО ВЩФШ ВМЙЪЛЙН Л 1,3 ФПТГПЧПЗП ЫБЗБ).
хЗМЩ ЪБГЕРМЕОЙС α ДМС РТПФЙЧПРПМПЦОЩИ УФПТПО ЪХВШЕЧ РПМХЮБАФУС ТБЪМЙЮОЩНЙ. пОЙ НЕОШЫЕ ДМС ЧПЗОХФПК УФПТПОЩ ЪХВШЕЧ ЫЕУФЕТОЙ Й УПРТСЦЕООПК ЧЩРХЛМПК УФПТПОЩ ЪХВШЕЧ ЛПМЕУБ Й УППФЧЕФУФЧЕООП ВПМШЫЕ ДМС РТПФЙЧПРПМПЦОЩИ УФПТПО. ч ЮЕТФЕЦБИ ДПУФБФПЮОП ХЛБЪЩЧБФШ УТЕДОЙК ХЗПМ α_УТ, ЛПФПТЩК ДМС РЕТЕДБЮ НБЫЙО ПВЭЕЗП НБЫЙОПУФТПЕОЙС Й МЕЗЛПЧЩИ БЧФПНПВЙМЕК z₁≥8 ПВЩЮОП РТЙОЙНБАФ ТБЧОЩН 21њ15′, Б ДМС РЕТЕДБЮ ФСЦЕМЩИ ФТБОУРПТФОЩИ НБЫЙО 22 30′.
чЩВПТ ОБРТБЧМЕОЙС ЪХВШЕЧ ЫЕУФЕТОЙ (РТБЧПЕ ЙМЙ МЕЧПЕ) ОЕ СЧМСЕФУС РТПЙЪЧПМШОЩН, Б ЪБЧЙУЙФ ПФ ОБРТБЧМЕОЙС ЗЙРПЙДОПЗП УНЕЭЕОЙС.
зЕПНЕФТЙЮЕУЛЙК ТБУЮЕФ ЗЙРПЙДОЩИ РЕТЕДБЮ БОБМПЗЙЮЕО ТБУЮЕФХ ЛПОЙЮЕУЛЙИ У ЛТХЗПЧЩНЙ ЪХВШСНЙ, ОП ОЕУЛПМШЛП УМПЦОЕЕ. рТЙ ТБУЮЕФЕ РПМШЪХАФУС ТБУЮЕФОЩНЙ ФБВМЙГБНЙ Й ЗТБЖЙЛБНЙ. пДЙО ЙЪ РБТБНЕФТПЧ РТЙИПДЙФУС ПРТЕДЕМСФШ РТЕДЧБТЙФЕМШОП, Б РПФПН ХФПЮОСФШ, Ф. Е. РПМШЪПЧБФШУС НЕФПДПН РПУМЕДПЧБФЕМШОПЗП РТЙВМЙЦЕОЙС.
рЕТЕДБФПЮОПЕ ЮЙУМП ЗЙРПЙДОЩИ РЕТЕДБЮ РП БОБМПЗЙЙ У ЧЙОФПЧЩНЙ ГЙМЙОДТЙЮЕУЛЙНЙ РЕТЕДБЮБНЙ:
(129)
ЗДЕ ß₁ Й ß₂ — ХЗМЩ ОБЛМПОБ ЪХВШЕЧ ЫЕУФЕТОЙ Й ЛПМЕУБ, РТЙЮЕН ß₁+ß₂≠ 90 фБЛ ЛБЛ ß₁ ЧЩВЙТБАФ ВПМШЫЙН, ЮЕН ß₂, ФП РТЙ ПДЙОБЛПЧЩИ ДЙБНЕФТБИ ЛПМЕУ d₂ Й РЕТЕДБФПЮОПН ЮЙУМЕ u ДЙБНЕФТ ЫЕУФЕТОЙ d1 ЗЙРПЙДОПК РЕТЕДБЮЙ РПМХЮБЕФУС Ч k=УПsß₂/УПsß₁ ТБЪ ВПМШЫЕ, ЮЕН Ч ЛПОЙЮЕУЛПК.
тБУЮЕФ ЗЙРПЙДОЩИ РЕТЕДБЮ РП ЛПОФБЛФОЩН ОБРТСЦЕОЙСН Й ОБ ЙЪЗЙВ НПЦОП РТПЙЪЧПДЙФШ ФБЛ ЦЕ, ЛБЛ ЛПОЙЮЕУЛЙИ, РТЙ ПДЙОБЛПЧЩИ ДЙБНЕФТБИ, ЫЙТЙОБИ Й ФПТГПЧЩИ НПДХМСИ.
рТЙ ЬФПН РП ЛПОФБЛФОПК РТПЮОПУФЙ РПМХЮБЕФУС ДПРПМОЙФЕМШОЩК ТЕУХТУ, ФБЛ ЛБЛ РТЙЧЕДЕООЩК ТБДЙХУ ЛТЙЧЙЪОЩ Ч ЗЙРПЙДОЩИ РЕТЕДБЮБИ РПМХЮБЕФУС Ч k 3 ТБЪ ВПМШЫЕ, ЮЕН Ч БОБМПЗЙЮОЩИ ЛПОЙЮЕУЛЙИ. рПМОЩК ЗЕПНЕФТЙЮЕУЛЙК Й РТПЮОПУФОПК ТБУЮЕФ ЗЙРПЙДОЩИ РЕТЕДБЮ РТЙЧЕДЕО Ч ТБВПФЕ.
рМБОЕФБТОЩНЙ ОБЪЩЧБАФ РЕТЕДБЮЙ, ЙНЕАЭЙЕ ЪХВЮБФЩЕ ЛПМЕУБ У РЕТЕНЕЭБАЭЙНЙУС ЗЕПНЕФТЙЮЕУЛЙНЙ ПУСНЙ. дЧЙЦЕОЙЕ ЬФЙИ ЛПМЕУ, ОБЪЩЧБЕНЩИ РМБОЕФБТОЩНЙ ЙМЙ УБФЕММЙФБНЙ, УИПДОП У ДЧЙЦЕОЙЕН РМБОЕФ, ПФЮЕЗП РЕТЕДБЮЙ Й РПМХЮЙМЙ УЧПЕ ОБЪЧБОЙЕ. уБФЕММЙФЩ ПВЛБФЩЧБАФУС РП ГЕОФТБМШОЩН ЛПМЕУБН, ЙНЕАЭЙН ЧОЕЫОЕЕ ЙМЙ ЧОХФТЕООЕЕ ЪБГЕРМЕОЙЕ. пУЙ УБФЕММЙФПЧ ЪБЛТЕРМЕОЩ Ч ЧПДЙМЕ Й ЧТБЭБАФУС ЧНЕУФЕ У ОЙН ЧПЛТХЗ ГЕОФТБМШОПК ПУЙ.
рМБОЕФБТОЩЕ РЕТЕДБЮЙ ЙНЕАФ ЫЙТПЛЙЕ ПВМБУФЙ ОБЪОБЮЕОЙС Й РТЙНЕОЕОЙС:
тЕДХГЙТПЧБОЙЕ УЛПТПУФЙ — УЙМПЧЩЕ РЕТЕДБЮЙ У НБМЩНЙ ХДЕМШОЩНЙ ЗБВБТЙФБНЙ Й НБУУПК, ЛЙОЕНБФЙЮЕУЛЙЕ РЕТЕДБЮЙ У ВПМШЫЙНЙ РЕТЕДБФПЮОЩНЙ ПФОПЫЕОЙСНЙ.
уМПЦЕОЙЕ Й ТБЪМПЦЕОЙЕ ДЧЙЦЕОЙС, Ч ФПН ЮЙУМЕ У БЧФПНБФЙЮЕУЛЙН ХРТБЧМЕОЙЕН УЛПТПУФЙ Ч УФБОЛБИ, БЧФПНПВЙМСИ Й ДТХЗЙИ НБЫЙОБИ, НОПЗПУФХРЕОЮБФЩЕ РМБОЕФБТОЩЕ ЛПТПВЛЙ УЛПТПУФЕК, ХРТБЧМСЕНЩЕ РППЮЕТЕДОЩН ФПТНПЦЕОЙЕН ЪЧЕОШЕЧ, ЪБНЛОХФЩЕ РМБОЕФБТОЩЕ РЕТЕДБЮЙ У ЧУФТПЕООПК ВЕУУФХРЕОЮБФПК РЕТЕДБЮЕК Й Ф. Д.
рТЕЙНХЭЕУФЧБ РМБОЕФБТОЩИ РЕТЕДБЮ (НБМЩЕ ЗБВБТЙФЩ Й НЕОШЫБС НБУУБ) ПВЯСУОСАФУС УМЕДХАЭЙНЙ РТЙЮЙОБНЙ:
ТБУРТЕДЕМЕОЙЕН ОБЗТХЪЛЙ НЕЦДХ УБФЕММЙФБНЙ, ВМБЗПДБТС ЮЕНХ ОБЗТХЪЛЙ ОБ ЪХВШСИ НЕОШЫЕ Ч ОЕУЛПМШЛП ТБЪ;
ВПМШЫЙН РЕТЕДБФПЮОЩН ПФОПЫЕОЙЕН Ч ПДОПК УФХРЕОЙ, ЮФП ЮБУФП РПЪЧПМСЕФ ОЕ РТЙВЕЗБФШ Л УМПЦОЩН НОПЗПУФХРЕОЮБФЩН РЕТЕДБЮБН;
ЫЙТПЛЙН РТЙНЕОЕОЙЕН РЕТЕДБЮ У ЧОХФТЕООЙН ЪБГЕРМЕОЙЕН, ПВМБДБАЭЙИ РПЧЩЫЕООПК ОЕУХЭЕК УРПУПВОПУФША.
лТПНЕ ФПЗП, Ч УЧСЪЙ У НЕОШЫЙНЙ ТБЪНЕТБНЙ РМБОЕФБТОЩЕ РЕТЕДБЮЙ ДПРХУЛБАФ ФЕТНЙЮЕУЛХА ПВТБВПФЛХ ЛПМЕУ ДП ВПМЕЕ ЧЩУПЛПК ФЧЕТДПУФЙ.
рМБОЕФБТОЩЕ РЕТЕДБЮЙ ТБВПФБАФ У НЕОШЫЙН ЫХНПН, ЮЕН РТПУФЩЕ, ЮФП УЧСЪБОП У РПЧЩЫЕООПК РМБЧОПУФША ЧОХФТЕООЕЗП ЪБГЕРМЕОЙС, НЕОШЫЙНЙ ТБЪНЕТБНЙ ЛПМЕУ, ЪБНЩЛБОЙЕН УЙМ Ч НЕИБОЙЪНЕ Й РЕТЕДБЮЕК НЕОШЫЙИ УЙМ ОБ ЛПТРХУ.
ъБФП РМБОЕФБТОЩЕ РЕТЕДБЮЙ ФТЕВХАФ РПЧЩЫЕООПК ФПЮОПУФЙ ЙЪЗПФПЧМЕОЙС, ЙНЕАФ, ЛБЛ РТБЧЙМП, ВПМШЫЕЕ ЮЙУМП ДЕФБМЕК Й УМПЦОЕЕ Ч УВПТЛЕ, ЮЕН РЕТЕДБЮЙ У ОЕРПДЧЙЦОЩНЙ ПУСНЙ.
рМБОЕФБТОЩЕ РЕТЕДБЮЙ ХДПВОП ЧУФТБЙЧБАФУС Ч ЬМЕЛФТПДЧЙЗБФЕМЙ, ИПДПЧЩЕ ЛПМЕУБ, ВБТБВБОЩ, ЫЛЙЧЩ.
рМБОЕФБТОЩЕ РЕТЕДБЮЙ Ч ОБУФПСЭЕЕ ЧТЕНС ЧЩРПМОСАФ ДМС НПНЕОФПЧ ДП 5·10 6 о·Н, У ЫЙТЙОПК ЪХВЮБФЩИ ЧЕОГПЧ ДП 800 НН.
оБЙВПМЕЕ ТБУРТПУФТБОЕООЩЕ ФЙРЩ РМБОЕФБТОЩИ РЕТЕДБЮ Й ЙИ ИБТБЛФЕТЙУФЙЛЙ РТЙЧЕДЕОЩ Ч ФБВМЙГЕ 20.
вПМШЫЙОУФЧП РТПУФЩИ РМБОЕФБТОЩИ РЕТЕДБЮ ЙНЕАФ РП ДЧБ ГЕОФТБМШОЩИ ЛПМЕУБ Й ЧПДЙМП, ХЮБУФЧХАЭЕЕ Ч РЕТЕДБЮЕ НПНЕОФПЧ (ПВПЪОБЮЕОЙЕ 2k-h, ТЙУХОПЛ 78). рТЙНЕОСАФ ФБЛЦЕ РЕТЕДБЮЙ У ФТЕНС ГЕОФТБМШОЩНЙ ЛПМЕУБНЙ Й ЧПДЙМПН, УМХЦБЭЙН ФПМШЛП ДМС РПДДЕТЦЙЧБОЙС УБФЕММЙФПЧ (ПВПЪОБЮЕОЙЕ ъk, ТЙУХОПЛ 79).
фБВМЙГБ 20. — пУОПЧОЩЕ ФЙРЩ РМБОЕФБТОЩИ РЕТЕДБЮ
рЕТЕДБЮБ У ЧЩУПЛЙН лрд, ИБТБЛФЕТОЩН ДМС УЙМПЧЩИ РЕТЕДБЮ, Й ПЗТБОЙЮЕООЩН ЙОФЕТЧБМПН РЕТЕДБФПЮОЩИ ПФОПЫЕОЙК. йНЕЕФ ЫЙТПЛПЕ РТЙНЕОЕОЙЕ Ч УЙМПЧЩИ Й ЧУРПНПЗБФЕМШОЩИ РТЙЧПДБИ. ч УЙМПЧЩИ РЕТЕДБЮБИ РТЙНЕОСАФ ПФ 2 ДП 20 УБФЕММЙФПЧ. пДОПТСДОБС (ПДОПУФХРЕОЮБФБС) РЕТЕДБЮБ РП УИЕНЕ 1 СЧМСЕФУС РТПУФЕКЫЕК Й ЙНЕЕФ НЙОЙНБМШОЩЕ ЗБВБТЙФЩ
рЕТЕДБЮБ У ДЧХИТСДОЩН УБФЕММЙФПН РП УИЕНЕ 2 ЙНЕЕФ ВПМШЫЙЕ ЛЙОЕНБФЙЮЕУЛЙЕ ЧПЪНПЦОПУФЙ ЪБ УЮЕФ ОЕЛПФПТПЗП ХУМПЦОЕОЙС ЛПОУФТХЛГЙЙ Й ОЕУЛПМШЛП ВПМШЫЙИ ПУЕЧЩИ ЗБВБТЙФПЧ
рЕТЕДБЮЙ, ЙНЕАЭЙЕ ВПМШЫЙЕ ЛЙОЕНБФЙЮЕУЛЙЕ ЧПЪНПЦОПУФЙ. рТЙНЕОСАФ РТЙ ОЕПВИПДЙНПУФЙ ВПМШЫЙИ РЕТЕДБФПЮОЩИ ПФОПЫЕОЙК Ч УМХЮБЕ, ЛПЗДБ лрд ОЕ ЙНЕЕФ ЪОБЮЕОЙС (ОБРТЙНЕТ, Ч РЕТЕДБЮБИ РТЙВПТПЧ). рТЙ ПЮЕОШ ВПМШЫЙИ РЕТЕДБФПЮОЩИ ПФОПЫЕОЙСИ НЗОПЧЕООПЕ РЕТЕДБФПЮОПЕ ПФОПЫЕОЙЕ НПЦЕФ УЙМШОП ЛПМЕВБФШУС Ч УЧСЪЙ У ВЙЕОЙСНЙ ЛПМЕУ
рЕТЕДБЮБ, Ч ЛПФПТПК ЧОЕЫОЙЕ НПНЕОФЩ ЧПУРТЙОЙНБАФУС ФТЕНС ГЕОФТБМШОЩНЙ ЛПМЕУБНЙ, Б ЧПДЙМП ФПМШЛП РПДДЕТЦЙЧБЕФ УБФЕММЙФЩ. рТЙ УТЕДОЙИ РЕТЕДБФПЮОЩИ ПФОПЫЕОЙСИ РТЙНЕОСЕФУС ДМС УЙМПЧЩИ РТЙЧПДПЧ, РТЙ ВПМШЫЙИ — ДМС ЧУРПНПЗБФЕМШОЩИ РТЙЧПДПЧ Й РТЙВПТПЧ. лПОУФТХЛГЙС УМПЦОЕЕ РТЕДЩДХЭЙИ
дЧХИУФХРЕОЮБФЩК ТЕДХЛФПТ, УПУФБЧМЕООЩК ЙЪ ДЧХИ ПДОПТСДОЩИ РЕТЕДБЮ. йНЕЕФ ЧЩУПЛЙК лрд. рТЙНЕОСЕФУС ДМС УЙМПЧЩИ РТЙЧПДПЧ Ч УМХЮБСИ, ЛПЗДБ РЕТЕДБФПЮОПЕ ПФОПЫЕОЙЕ РЕТЕДБЮ РП УИЕНБН 1 Й 2 ОЕДПУФБФПЮОП
рЕТЕДБЮБ, ДПРХУЛБАЭБС Ч ПДОПК РБТЕ ЪОБЮЙФЕМШОЩЕ РЕТЕДБФПЮОЩЕ ПФОПЫЕОЙС. чЕДХЭЙК ЧБМ РТЙЧПДЙФ ЧПДЙМП. чТБЭЕОЙЕ УБФЕММЙФПЧ, УГЕРМЕООЩИ У ОЕРПДЧЙЦОЩН ЛПМЕУПН 2, РЕТЕДБЕФУС ЮЕТЕЪ РБМШГЩ ЧЕДПНПНХ ЧБМХ. ч РЕТЕДБЮЕ ЙУРПМШЪХЕФУС ЬЧПМШ-ЧЕОФОПЕ ЪБГЕРМЕОЙЕ ЙМЙ ГЕЧПЮОПЕ, РПЪЧПМСАЭЕЕ ХНЕОШЫЙФШ ЗБВБТЙФЩ Й РПЧЩУЙФШ лрд ТЕДХЛФПТБ
рМБОЕФБТОЩЕ РЕТЕДБЮЙ РП ЙИ ЛЙОЕНБФЙЮЕУЛЙН ЧПЪНПЦОПУФСН НПЦОП ТБЪВЙФШ ОБ УМЕДХАЭЙЕ ЗТХРРЩ:
рТПУФЩЕ РЕТЕДБЮЙ У ОЕВПМШЫЙНЙ РЕТЕДБФПЮОЩНЙ ПФОПЫЕОЙСНЙ, ОП У ЧЩУПЛЙН лрд (УИЕНЩ 1, 2 Ч ФБВМЙГЕ 20 Й ТЙУХОПЛ78). рЕТЕДБЮЙ РТЙЗПДОЩ ДМС УЙМПЧЩИ РТЙЧПДПЧ.
рТПУФЩЕ РЕТЕДБЮЙ У ВПМШЫЙН ЙОФЕТЧБМПН РЕТЕДБФПЮОЩИ ПФОПЫЕОЙК, ОП У РПОЙЦЕООЩН лрд (УИЕНЩ 3, 4 Ч ФБВМЙГЕ 20). х ЬФЙИ РЕТЕДБЮ РТЙЧЕДЕООЩЕ НЕИБОЙЪНЩ ЙНЕАФ РПМПЦЙФЕМШОЩЕ РЕТЕДБФПЮОЩЕ ПФОПЫЕОЙС. рПЬФПНХ ЖПТНХМЩ ДМС РЕТЕДБФПЮОЩИ ПФОПЫЕОЙК РМБОЕФБТОЩИ РЕТЕДБЮ ЙНЕАФ ПФТЙГБФЕМШОЩЕ ЮМЕОЩ, РПЪЧПМСАЭЙЕ ЧБТШЙТПЧБФШ РЕТЕДБФПЮОЩЕ ПФОПЫЕОЙС Ч ЫЙТПЛЙИ РТЕДЕМБИ Й РПМХЮБФШ ЪОБЮЙФЕМШОХА ТЕДХЛГЙА,
лПНВЙОЙТПЧБООЩЕ РЕТЕДБЮЙ, УПУФБЧМСЕНЩЕ ЙЪ ДЧХИ РТПУФЩИ ЪХВЮБФЩИ РМБОЕФБТОЩИ РЕТЕДБЮ ЙМЙ ЪХВЮБФПК РМБОЕФБТОПК РЕТЕДБЮЙ Й НЕИБОЙЪНБ РБТБММЕМШОЩИ ЛТЙЧПЫЙРПЧ Й Ф. Д. (УИЕНЩ 5, 6, 7, ФБВМЙГЕ 20). х ОЙИ ТБУЫЙТЕООЩЕ ЧПЪНПЦОПУФЙ. дЧХИУФХРЕОЮБФЩЕ РЕТЕДБЮЙ ГЕМЕУППВТБЪОП ЧЩРПМОСФШ У ПДЙОБЛПЧЩНЙ ТБДЙХУБНЙ ЧПДЙМ.
рТЙ РТПЕЛФЙТПЧБОЙЙ РМБОЕФБТОЩИ РЕТЕДБЮ ПЮЕОШ ЧБЦОП ЧЩВТБФШ ПРФЙНБМШОХА УИЕНХ, ФБЛ ЛБЛ РМБОЕФБТОЩЕ РЕТЕДБЮЙ ТБЪОЩИ УИЕН ДМС ПДОПК Й ФПК ЦЕ ГЕМЙ НПЗХФ ЙНЕФШ УХЭЕУФЧЕООП ТБЪМЙЮОЩЕ ЗБВБТЙФЩ Й Ч ОЕУЛПМШЛП ТБЪ ПФМЙЮБАЭЙЕУС РПФЕТЙ.
лрд РМБОЕФБТОЩИ РЕТЕДБЮ ПВЩЮОП ТЕЪЛП РБДБЕФ У ТПУФПН РЕТЕДБФПЮОПЗП ПФОПЫЕОЙС (УН. ФБВМЙГХ 20). рТЙ ОЕПВИПДЙНПУФЙ РПМХЮЕОЙС РПЧЩЫЕООПЗП лрд ЙОПЗДБ ПЛБЪЩЧБЕФУС ГЕМЕУППВТБЪОЩН УПЕДЙОСФШ РМБОЕФБТОХА РЕТЕДБЮХ У ОЕ РМБОЕФБТОПК ЙМЙ ДБЦЕ РПУМЕДПЧБФЕМШОП УПЕДЙОСФШ ДЧЕ РМБОЕФБТОЩЕ РЕТЕДБЮЙ (УН. ТЙУХОПЛ 79).
ч РМБОЕФБТОЩИ РЕТЕДБЮБИ ЫЙТПЛП РТЙНЕОСАФ ЪХВЮБФЩЕ РБТЩ У ЧОХФТЕООЙН ЪБГЕРМЕОЙЕН. хНЕОШЫБС ТБЪОПУФЙ ЮЙУЕМ ЪХВШЕЧ ЛПМЕУ У ЧОХФТЕООЙН ЪБГЕРМЕОЙЕН, НПЦОП ЪОБЮЙФЕМШОП ТБУЫЙТЙФШ ЛЙОЕНБФЙЮЕУЛЙЕ ЧПЪНПЦОПУФЙ РЕТЕДБЮ.
рТЙНЕОСС РЕТЕДБ У ХЗМПН ЪБГЕРМЕОЙС α=30њ Й ЛПЬЖЖЙГЙЕОФПН ЧЩУПФЩ ЗПМПЧЛЙ h_a=0.75 НПЦОП ДПЧЕУФЙ ТБЪОПУФШ ЮЙУЕМ ЪХВШЕЧ ДП 3, Б ЕЭЕ ОЕВПМШЫЙН ДПРПМОЙФЕМШОЩН ХНЕОШЫЕОЙЕН ЧЩУПФЩ ЗПМПЧЛЙ ЪХВШЕЧ — ДП 2. хЗМПЧПК ЛПТТЕЛГЙЕК ЪБГЕРМЕОЙС, ОБТЕЪБЕНПЗП ОПТНБМШОЩН ДЧБДГБФЙЗТБДХУОЩН ДПМВСЛПН, НПЦОП ДПЧЕУФЙ ТБЪОПУФШ ЮЙУЕМ ЪХВШЕЧ ДП 1, ОП У РПОЙЦЕООЩН лрд.
ч ГЕЧПЮОЩИ РМБОЕФБТОЩИ РЕТЕДБЮБИ (РТПЕЛФЙТХЕНЩИ РП УИЕНЕ 7, ФБВМЙГБ 20) УПМОЕЮОПЕ ЛПМЕУП ЧЩРПМОСАФ У ГЕЧЛБНЙ (ТПМЙЛБНЙ ОБ ПУСИ), Б ЪХВШС УБФЕММЙФПЧ ПЮЕТЮЙЧБАФ РП ЬЛЧЙДЙУФБОФБН Л ЬРЙГЙЛМПЙДБН. тБЪОПУФШ ЮЙУЕМ ГЕЧПЛ Й ЪХВШЕЧ ПВЩЮОП ТБЧОБ 1.
уХЭЕУФЧЕООПЕ РПЧЩЫЕОЙЕ ЛБЮЕУФЧЕООЩИ РПЛБЪБФЕМЕК РМБОЕФБТОЩИ РЕТЕДБЮ ДПУФЙЗБЕФУС РХФЕН ХУФТБОЕОЙС ЙЪВЩФПЮОЩИ УЧСЪЕК.
дМС ХУФТБОЕОЙС ЛПОГЕОФТБГЙЙ ОБЗТХЪЛЙ РП РПФПЛБН Й ДМЙОЕ ЪХВШЕЧ УМЕДХЕФ ХУФБОБЧМЙЧБФШ ПДОПЧЕОГПЧЩЕ УБФЕММЙФЩ ОБ УЖЕТЙЮЕУЛЙИ РПДЫЙРОЙЛБИ Й ДЕМБФШ УПМОЕЮОПЕ ЛПМЕУП РМБЧБАЭЙН.
тЙУХОПЛ 78 — пДОПТСДОБС РМБОЕФБТОБС РЕТЕДБЮБ РП УИЕНЕ 1, ФБВМЙГБ 20. тЙУХОПЛ 79 — рМБОЕФБТОБС РЕТЕДБЮБ РП УИЕНЕ 6, ФБВМЙГБ 20.
рТЙНЕОСАФ ФБЛЦЕ РМБОЕФБТОЩЕ РЕТЕДБЮЙ У ЧЩТБЧОЙЧБОЙЕН ОБЗТХЪЛЙ НЕЦДХ РПФПЛБНЙ ЪБ УЮЕФ РПДБФМЙЧПУФЙ ЧПДЙМБ ЙМЙ ПВПДБ У ЧОХФТЕООЙНЙ ЪХВШСНЙ.
тБУЮЕФ РМБОЕФБТОЩИ РЕТЕДБЮ. ъХВЮБФЩЕ ЛПМЕУБ РМБОЕФБТОЩИ РЕТЕДБЮ НПЦОП ТБУУЮЙФЩЧБФШ ФБЛ ЦЕ, ЛБЛ ОЕ РМБОЕФБТОЩИ.
юЙУМБ ЪХВШЕЧ ЛПМЕУ ПРТЕДЕМСАФ ЙУИПДС ЙЪ ЪБДБООПЗП РЕТЕДБФПЮОПЗП ПФОПЫЕОЙС (УН. ФБВМЙГХ 20) Й ХУМПЧЙК:
УППУОПУФЙ z₂=0,5(z₃-z ₁) ;
УПВЙТБЕНПУФЙ (z₁+z₃)/n_c= ГЕМПЕ ЮЙУМП;
УПУЕДУФЧБ z₂+2 тЙУХОПЛ 80 — уИЕНБ ЧПМОПЧПК РЕТЕДБЮЙ.
рТЙОГЙР ЧПМОПЧЩИ РЕТЕДБЮ ЪБЛМАЮБЕФУС Ч НОПЗПРБТОПУФЙ ЪБГЕРМЕОЙС ЪХВШЕЧ, ЛПФПТБС ПРТЕДЕМСЕФ ЧУЕ РПМПЦЙФЕМШОЩЕ ЛБЮЕУФЧБ ЬФЙИ РЕТЕДБЮ РП УТБЧОЕОЙА У ДТХЗЙНЙ.
чПМОПЧЩЕ РЕТЕДБЮЙ Ч УТБЧОЕОЙЙ У ПВЩЮОЩНЙ ЪХВЮБФЩНЙ ЙНЕАФ НЕОШЫХА НБУУХ Й НЕОШЫЙЕ ЗБВБТЙФЩ, ПВЕУРЕЮЙЧБАФ ВПМЕЕ ЧЩУПЛХА ЛЙОЕНБФЙЮЕУЛХА ФПЮОПУФШ, ЙНЕАФ НЕОШЫЙК НЕТФЧЩК ИПД, ПВМБДБАФ ЧЩУПЛПК ДЕНРЖЙТХАЭЕК УРПУПВОПУФША (Ч 4-5 ТБЪ ВПМШЫЕК, ЮЕН Х ПВЩЮОЩИ), ТБВПФБАФ У НЕОШЫЙН ЫХНПН.
рТЙ ОЕПВИПДЙНПУФЙ ЧПМОПЧЩЕ РЕТЕДБЮЙ РПЪЧПМСАФ РЕТЕДБЧБФШ ДЧЙЦЕОЙЕ Ч ЗЕТНЕФЙЪЙТПЧБООПЕ РТПУФТБОУФЧП ВЕЪ РТЙНЕОЕОЙС УБМШОЙЛПЧ.
чПМОПЧЩЕ РЕТЕДБЮЙ РПЪЧПМСАФ ПУХЭЕУФЧМСФШ ВПМШЫЙЕ РЕТЕДБФПЮОЩЕ ПФОПЫЕОЙС Ч ПДОПК УФХРЕОЙ; РТЙ ЪХВЮБФЩИ ЛПМЕУБИ ЙЪ УФБМЙ u_min=60 (ПЗТБОЙЮЙЧБЕФУС РТПЮОПУФША РТЙ ЙЪЗЙВЕ ЗЙВЛПЗП ЛПМЕУБ) Й u_max=300 (ПЗТБОЙЮЙЧБЕФУС НЙОЙНБМШОП ДПРХУФЙНПК ЧЕМЙЮЙОПК НПДХМС, ТБЧОПК 0,2:0,15 НН). рТЙ ЬФПН лрд ТБЧЕО 80. 90 %, ЛБЛ Й Ч РМБОЕФБТОЩИ РЕТЕДБЮБИ У ФЕН ЦЕ РЕТЕДБФПЮОЩН ПФОПЫЕОЙЕН. л ОЕДПУФБФЛБН ЧПМОПЧЩИ РЕТЕДБЮ НПЦОП ПФОЕУФЙ ПЗТБОЙЮЕООЩЕ ЮБУФПФЩ ЧТБЭЕОЙС ЧЕДХЭЕЗП ЧБМБ ЗЕОЕТБФПТБ ЧПМО РТЙ ВПМШЫЙИ ДЙБНЕФТБИ ЛПМЕУ (ЧП ЙЪВЕЦБОЙЕ ВПМШЫЙИ ПЛТХЦОЩИ УЛПТПУФЕК ЗЕОЕТБФПТБ), НЕМЛЙЕ НПДХМЙ ЪХВЮБФЩИ ЛПМЕУ (0,15. 2 НН). рТЙ УЕТЙКОПН ЙЪЗПФПЧМЕОЙЙ Ч УРЕГЙБМЙЪЙТПЧБООПН РТПЙЪЧПДУФЧЕ ЧПМОПЧЩЕ РЕТЕДБЮЙ ДЕЫЕЧМЕ РМБОЕФБТОЩИ. лТХФЙМШОБС ЦЕУФЛПУФШ ЧПМОПЧЩИ РЕТЕДБЮ ОЕУЛПМШЛП НЕОШЫЕ РТПУФЩИ ЪХВЮБФЩИ, ОП ПВЩЮОП СЧМСЕФУС ДПУФБФПЮОПК.
оБ ТЙУХОЛЕ 80 ЗЙВЛЙК ЧЕОЕГ 1 ОБТЕЪБО ОБ ДЕЖПТНЙТХЕНПН ЛПОГЕ ФПОЛПК ГЙМЙОДТЙЮЕУЛПК ПВПМПЮЛЙ 5, ДТХЗПК ЛПОЕГ ЛПФПТПК ЮЕТЕЪ ФПОЛПЕ ДОП УПЕДЙОСЕФУС У ЧЩИПДОЩН ЧБМПН 4.
зЕОЕТБФПТ ЧПМО 3 УПУФПЙФ ЙЪ ПЧБМШОПЗП ЛХМБЮЛБ УППФЧЕФУФЧХАЭЕЗП РТПЖЙМС Й УРЕГЙБМШОПЗП ЫБТЙЛПРПДЫЙРОЙЛБ 6 У ЗЙВЛЙНЙ ЛПМШГБНЙ. йОПЗДБ ЧЩРПМОСАФ ЗЕОЕТБФПТ ЧПМО Ч ЧЙДЕ ДЧХИ ДЙУЛПЧ (ТПМЙЛПЧ), ТБУРПМПЦЕООЩИ ОБ ЧБМХ ЙМЙ Ч ЧЙДЕ ЮЕФЩТЕИ ТПМЙЛПЧ. уВПТЛХ ЪБГЕРМЕОЙС НПЦОП ПУХЭЕУФЧЙФШ ФПМШЛП РПУМЕ ДЕЖПТНБГЙЙ ЗЙВЛПЗП ЛПМЕУ.
оБ ЛПОГБИ ВПМШЫПК ПУЙ ЧБМБ ЪХВШС ЪБГЕРМСАФУС РП ЧУЕК ЧЩУПФЕ, ОБ НБМПК ПУЙ ЪХВШС ОЕ ЪБГЕРМСАФУС. нЕЦДХ ЬФЙНЙ ХЮБУФЛБНЙ ЪХВШС ЗЙВЛПЗП ЛПМЕУБ РПЗТХЦЕОЩ ЧП ЧРБДЙОЩ ЦЕУФЛПЗП ЛПМЕУБ ОБ ТБЪОХА ЗМХВЙОХ. ъБГЕРМЕОЙЕ ОБРПНЙОБЕФ ЫМЙГЕЧПЕ УПЕДЙОЕОЙЕ.
рТЙ ЧТБЭЕОЙЙ ЗЕОЕТБФПТБ ЧПМО ЗЙВЛЙК ЪХВЮБФЩК ЧЕОЕГ ПВЛБФЩЧБЕФУС РП ОЕРПДЧЙЦОПНХ ЛПМЕУХ, ЧТБЭБС ПВПМПЮЛХ Й ЧБМ. рТЙОГЙР ТБВПФЩ ЧПМОПЧПК РЕТЕДБЮЙ БОБМПЗЙЮЕО РМБОЕФБТОПК РЕТЕДБЮЕ У РБТБММЕМШОЩНЙ ЛТЙЧПЫЙРБНЙ (УИЕНБ 7. ФБВМ. 20).
тБДЙБМШОЩЕ РЕТЕНЕЭЕОЙС w ЗЙВЛПЗП ЛПМЕУБ РП ПЛТХЦОПУФЙ ЙНЕАФ ДЧБ НБЛУЙНХНБ Й ДЧБ НЙОЙНХНБ, Ф. Е. ДЧЕ ЧПМОЩ. рПЬФПНХ РЕТЕДБЮХ ОБЪЩЧБАФ ДЧХИЧПМОПЧПК. чПЪНПЦОЩ ФТЕИЧПМОПЧЩЕ РЕТЕДБЮЙ, ОП ЙИ РТЙНЕОСАФ ТЕДЛП, ФБЛ ЛБЛ Ч ФТЕИЧПМОПЧПК РЕТЕДБЮЕ ЧЩЫЕ ОБРТСЦЕОЙС ЙЪЗЙВБ Ч ЗЙВЛПН ЛПМЕУЕ.
еУМЙ ПВПМПЮЛБ ОЕРПДЧЙЦОП УПЕДЙОЕОБ У ЛПТРХУПН, ФП ЧТБЭЕОЙЕ ПФ ЗЕОЕТБФПТБ РЕТЕДБЕФУС ЦЕУФЛПНХ ЛПМЕУХ У ЧОХФТЕООЙНЙ ЪХВШСНЙ. ч УИЕНЕ ДМС РЕТЕДБЮЙ ДЧЙЦЕОЙС Ч ЗЕТНЕФЙЪЙТПЧБООПЕ РТПУФТБОУФЧП ЗЙВЛПЕ ЛПМЕУП ЙНЕЕФ ЪХВЮБФЩК ЧЕОЕГ, ТБУРПМПЦЕООЩК Ч УЕТЕДЙОЕ ХДМЙОЕООПЗП ГЙМЙОДТЙЮЕУЛПЗП УФБЛБОБ, МЕЧЩК ЖМБОЕГ ЛПФПТПЗП ЗЕТНЕФЙЮОП УПЕДЙОЕО У ЛПТРХУПН. чТБЭЕОЙЕ РЕТЕДБЕФУС ПФ ЗЕОЕТБФПТБ ЧПМО Л ЦЕУФЛПНХ ЛПМЕУХ z₂, ЧЩРПМОЕООПНХ Ч ЧЙДЕ УФБЛБОБ, ПИЧБФЩЧБАЭЕЗП ЮБУФШ ЗЙВЛПЗП ЛПМЕУБ.
рЕТЕДБЮЙ (УН. ТЙУХОПЛ 80) НПЗХФ ТБВПФБФШ Ч ЛБЮЕУФЧЕ ТЕДХЛФПТБ (лрд 80: 90 %) Й НХМШФЙРМЙЛБФПТБ (лрд 60. 70%). ч РЕТЧПН УМХЮБЕ ЧЕДХЭЙН ЪЧЕОПН СЧМСЕФУС ЗЕОЕТБФПТ ЧПМО, ЧП ЧФПТПН — ЧБМ ЗЙВЛПЗП ЙМЙ ЦЕУФЛПЗП ЛПМЕУБ.
рЕТЕДБФПЮОПЕ ПФОПЫЕОЙЕ ЧПМОПЧЩИ РЕТЕДБЮ ПРТЕДЕМСЕФУС ФБЛ ЦЕ, ЛБЛ Й ДМС РМБОЕФБТОЩИ, РП ХТБЧОЕОЙА чЙММЙУБ.
рТЙ ОЕРПДЧЙЦОПН ЦЕУФЛПН ЛПМЕУЕ 2 (УН. ТЙУХОПЛ 80):
(130)
ЪОБЛ НЙОХУ ХЛБЪЩЧБЕФ ОБ ТБЪОЩЕ ОБРТБЧМЕОЙС ЧТБЭЕОЙС ЧЕДХЭЕЗП Й ЧЕДПНПЗП ЪЧЕОШЕЧ.
рТЙ ОЕРПДЧЙЦОПН ЗЙВЛПН ЛПМЕУЕ (УН. ТЙУХОПЛ 81):
(131)
ЗДЕ n_o, n₁ (n ₂) — ЮБУФПФЩ ЧТБЭЕОЙС ЧЕДХЭЕЗП Й ЧЕДПНЩИ ЪЧЕОШЕЧ;
z₁, z₂ — ЮЙУМБ ЪХВШЕЧ ЛПМЕУ ЗЙВЛПЗП Й ЦЕУФЛПЗП УППФЧЕФУФЧЕООП.
тЙУХОПЛ 81 — уИЕНБ ЧПМОПЧПК РЕТЕДБЮЙ ДЧЙЦЕОЙС Ч ЗЕТНЕФЙЪЙТПЧБООПЕ РТПУФТБОУФЧП.
тБЪОПУФШ ЪХВШЕЧ ЛПМЕУ ДПМЦОБ ВЩФШ ТБЧОБ ЙМЙ ЛТБФОБ ЮЙУМХ ЧПМО (ЛБЛ Ч РМБОЕФБТОПК РЕТЕДБЮЕ — ЮЙУМХ УБФЕММЙФПЧ), Ф. Е.:
ЗДЕ n_w — ЮЙУМП ЧПМО, ПВЩЮОП ТБЧОПЕ 2;
k_z — ЛПЬЖЖЙГЙЕОФ ЛТБФОПУФЙ, ПВЩЮОП ТБЧОЩК ЕДЙОЙГЕ; РТЙ u тЙУХОПЛ 82 — чПМОПЧПК ЪХВЮБФЩК ТЕДХЛФПТ.
ч уыб, сРПОЙЙ ОБМБЦЕОП УЕТЙКОПЕ РТПЙЪЧПДУФЧП ЧПМОПЧЩИ ТЕДХЛФПТПЧ ПВЭЕЗП ОБЪОБЮЕОЙС.
тБЪТБВПФБО УФБОДБТФОЩК ТСД ТЕДХЛФПТПЧ Ч тПУУЙЙ. уФБОДБТФОЩК ТСД УПДЕТЦЙФ 11 ФЙРПТБЪНЕТПЧ (ДЙБНЕФТЩ ДЕМЙФЕМШОЩИ ПЛТХЦОПУФЕК ЗЙВЛПЗП ЬМЕНЕОФБ ОБИПДСФУС Ч ДЙБРБЪПОЕ 50,8-508 НН). ч ЛБЦДПН ФЙРПТБЪНЕТЕ ТЕДХЛФПТЩ ЙНЕАФ ЮЕФЩТЕ ЙМЙ Ч УТЕДОЕН ДЙБРБЪПОЕ (80-320 НН) УЕНШ РЕТЕДБФПЮОЩИ ПФОПЫЕОЙК, РПМХЮБЕНЩИ ЪБ УЮЕФ ЙЪНЕОЕОЙС НПДХМС Й ЮЙУМБ ЪХВШЕЧ.
нБЛУЙНБМШОБС ЮБУФПФБ ЧТБЭЕОЙС ЗЕОЕТБФПТБ ЧПМО У ЫБТЙЛПРПДЫЙРОЙЛПН 3500 НЙО -1 ДМС ДЙБНЕФТПЧ ЗЙВЛЙИ ЛПМЕУ 50,8. 203 НН Й 1750 НЙО -1 ДМС ДЙБНЕФТПЧ 254. 407 НН. юБУФПФБ ЧТБЭЕОЙС ПЗТБОЙЮЙЧБЕФУС ФЕНРЕТБФХТПК ОБЗТЕЧБ Й ТБВПФПУРПУПВОПУФША РПДЫЙРОЙЛБ ЗЕОЕТБФПТБ ЧПМО.
дЙБРБЪПО РЕТЕДБЧБЕНЩИ ЧТБЭБАЭЙИ НПНЕОФПЧ 30. 30000 о Н, НПЭОПУФЕК 0,095:48 ЛчФ.
ч ОБЫЕК УФТБОЕ ТБЪТБВПФБОЩ Й ЙУРЩФБОЩ ТЕДХЛФПТЩ У РЕТЕДБЧБЕНЩН НПНЕОФПН 150000о Н.
тБУЮЕФ ЧПМОПЧЩИ ЪХВЮБФЩИ РЕТЕДБЮ ПФМЙЮБЕФУС ПФ ТБУЮЕФБ ПВЩЮОЩИ ЪХВЮБФЩИ РЕТЕДБЮ ФЕН, ЮФП ХЮЙФЩЧБЕФ ЙЪНЕОЕОЙС РЕТЧПОБЮБМШОПК ЖПТНЩ ЪХВЮБФЩИ ЧЕОГПЧ Й ЗЕОЕТБФПТБ ЧПМО ПФ ХРТХЗЙИ ДЕЖПТНБГЙК.
ьЛУРЕТЙНЕОФБМШОЩЕ ЙУУМЕДПЧБОЙС РПЛБЪЩЧБАФ, ЮФП ЧПМОПЧЩЕ РЕТЕДБЮЙ УФБОПЧСФУС ОЕТБВПФПУРПУПВОЩНЙ РП УМЕДХАЭЙН РТЙЮЙОБН.
тБЪТХЫЕОЙЕ РПДЫЙРОЙЛПЧ ЗЕОЕТБФПТБ ЧПМО ПФ ОБЗТХЪЛЙ Ч ЪБГЕРМЕОЙЙ ЙМЙ ЙЪ-ЪБ ЪОБЮЙФЕМШОПЗП РПЧЩЫЕОЙС ФЕНРЕТБФХТЩ.
рПЧЩЫЕОЙЕ ФЕНРЕТБФХТЩ НПЦЕФ ЧЩЪЧБФШ ОЕДПРХУФЙНПЕ ХНЕОШЫЕОЙЕ ЪБЪПТБ НЕЦДХ ЗЕОЕТБФПТПН Й ЗЙВЛЙН ЪХВЮБФЩН ЧЕОГПН. оПНЙОБМШОЩК ЪБЪПТ ОБ ДЙБНЕФТ РТЙНЕТОП ТБЧЕО 0,00015 ДЙБНЕФТБ ПВПМПЮЛЙ. чПЪТБУФБОЙЕ ОБЗТХЪЛЙ Й ФЕНРЕТБФХТЩ Ч ОЕЛПФПТЩИ УМХЮБСИ УЧСЪБОП У ЙОФЕТЖЕТЕОГЙЕК ЧЕТЫЙО ЪХВШЕЧ ОБ ЧИПДЕ Ч ЪБГЕРМЕОЙЕ, РПСЧМСАЭЕКУС РТЙ ВПМШЫЙИ ЙЪНЕОЕОЙСИ РЕТЧПОБЮБМШОПК ЖПТНЩ ЗЕОЕТБФПТБ ЧПМО, ЗЙВЛПЗП Й ЦЕУФЛПЗП ЪХВЮБФЩИ ЧЕОГПЧ.
рТПУЛПЛ ЗЕОЕТБФПТБ ЧПМО РТЙ ВПМШЫЙИ ЛТХФСЭЙИ НПНЕОФБИ (РП БОБМПЗЙЙ У РТЕДПИТБОЙФЕМШОПК НХЖФПК). рТПУЛПЛ УЧСЪБО У ЙЪНЕОЕОЙЕН ЖПТНЩ ЗЕОЕТБФПТБ ЧПМО, ЗЙВЛПЗП Й ЦЕУФЛПЗП ЪХВЮБФЩИ ЧЕОГПЧ РПД ОБЗТХЪЛПК ЧУМЕДУФЧЙЕ ЙИ ОЕДПУФБФПЮОПК ТБДЙБМШОПК ЦЕУФЛПУФЙ ЙМЙ РТЙ ВПМШЫЙИ ПФЛМПОЕОЙСИ ТБДЙБМШОЩИ ТБЪНЕТПЧ ЗЕОЕТБФПТБ. рТПУЛПЛ ОБУФХРБЕФ ФПЗДБ, ЛПЗДБ ЪХВШС ОБ ЧИПДЕ Ч ЪБГЕРМЕОЙЕ ХРЙТБАФУС ПДЙО Ч ДТХЗПК РПЧЕТИОПУФСНЙ ЧЕТЫЙО. рТЙ ЬФПН ЗЕОЕТБФПТ ЧПМО УЦЙНБЕФУС, Б ЦЕУФЛПЕ ЛПМЕУП ТБУРЙТБЕФУС Ч ТБДЙБМШОПН ОБРТБЧМЕОЙЙ, ЮФП РТЙЧПДЙФ Л РТПУЛПЛХ.
дМС РТЕДПФЧТБЭЕОЙС РТПУЛПЛБ ТБДЙБМШОПЕ ХРТХЗПЕ РЕТЕНЕЭЕОЙЕ ЗЙВЛПЗП ЛПМЕУБ РТЕДХУНБФТЙЧБАФ ВПМШЫЕ ОПНЙОБМШОПЗП, Б ЪБГЕРМЕОЙЕ УПВЙТБАФ У ОБФСЗПН ЙМЙ ХЧЕМЙЮЙЧБАФ ТБЪНЕТЩ РЕТЕДБЮЙ.
рПМПНЛБ ЗЙВЛПЗП ЛПМЕУБ ПФ ФТЕЭЙО ХУФБМПУФЙ, РПСЧМСАЭЙИУС ЧДПМШ ЧРБДЙО ЪХВЮБФПЗП ЧЕОГБ РТЙ ОБРТСЦЕОЙСИ, РТЕЧЩЫБАЭЙИ РТЕДЕМ ЧЩОПУМЙЧПУФЙ. у ХЧЕМЙЮЕОЙЕН ФПМЭЙОЩ ЗЙВЛПЗП ЛПМЕУБ ОБРТСЦЕОЙС Ч ОЕН ПФ РПМЕЪОПЗП РЕТЕДБЧБЕНПЗП НПНЕОФБ ХНЕОШЫБАФУС, Б ПФ ДЕЖПТНЙТПЧБОЙС ЗЕОЕТБФПТПН ЧПМО ХЧЕМЙЮЙЧБАФУС. рПЬФПНХ ЕУФШ ПРФЙНБМШОБС ФПМЭЙОБ.
дПМЗПЧЕЮОПУФШ ЗЙВЛПЗП ЬМЕНЕОФБ МЕЗЛП ПВЕУРЕЮЙЧБЕФУС РТЙ РЕТЕДБФПЮОПН ПФОПЫЕОЙЙ Ч УФХРЕОЙ u>ф20 Й ЮТЕЪЧЩЮБКОП ФТХДОП РТЙ u 100. 120 ОЕУХЭБС УРПУПВОПУФШ ПВЩЮОП ПЗТБОЙЮЙЧБЕФУС УФПКЛПУФША РПДЫЙРОЙЛБ ЗЕОЕТБФПТБ ЧПМО; РТЙ u 100-РТПЮОПУФША ЗЙВЛПЗП ЬМЕНЕОФБ, РТЙЮЕН ХТПЧЕОШ ОБРТСЦЕОЙК ПРТЕДЕМСЕФУС Ч РЕТЧХА ПЮЕТЕДШ ЧЕМЙЮЙОПК ТБДЙБМШОПЗП ХРТХЗПЗП РЕТЕНЕЭЕОЙС wП Й Ч НЕОШЫЕК УФЕРЕОЙ ЧТБЭБАЭЙН НПНЕОФПН.
нБЛУЙНБМШОП ДПРХУФЙНЩК ЧТБЭБАЭЙК НПНЕОФ УЧСЪБО У РПДБФМЙЧПУФША ЪЧЕОШЕЧ.
хДПВОП ЪБ ЛТЙФЕТЙК ТБВПФПУРПУПВОПУФЙ ХУМПЧОП РТЙОСФШ ДПРХУФЙНЩЕ ОБРТСЦЕОЙС УНСФЙС [σ]_УН ОБ ВПЛПЧЩИ РПЧЕТИОПУФСИ ЪХВШЕЧ РП БОБМПЗЙЙ УП ЫМЙГЕЧЩНЙ УПЕДЙОЕОЙСНЙ:
(137)
(138)
ЗДЕ ф — ЧТБЭБАЭЙК НПНЕОФ ОБ ФЙИПИПДОПН ЧБМХ РЕТЕДБЮЙ, о· Н;
d-ДЙБНЕФТ ДЕМЙФЕМШОПК ПЛТХЦОПУФЙ ЗЙВЛПЗП ЪХВЮБФПЗП ЧЕОГБ, НН;
-ЛПЬЖЖЙГЙЕОФ ЫЙТЙОЩ ЪХВЮБФПЗП ЧЕОГБ (ВЕТЕФУС 0,2. 0,18 ДМС УЙМПЧЩИ, 0,15. 0,1 ДМС НБМПОБЗТХЦЕООЩИ Й ЛЙОЕНБФЙЮЕУЛЙИ РЕТЕДБЮ);
л — ЛПЬЖЖЙГЙЕОФ, ЪБЧЙУСЭЙК ПФ ТЕЦЙНБ ТБВПФЩ, ТБЧОЩК:
РТЙ УРПЛПКОПК ОБЗТХЪЛЕ (ф_max / T -1 ; ПФ ТБЪНЕТПЧ РЕТЕДБЮЙ d.
(140)
(141)
K_d=l,25 РТЙ d 130 НН.
ч УТЕДОЙИ ХУМПЧЙСИ [σ]_УН ДМС УФБМШОЩИ ЛПМЕУ 10. 20, ДМС РМБУФНБУУПЧЩИ 3. 15 нрБ; РТЙ НБМЩИ УЛПТПУФСИ ЗЕОЕТБФПТБ ХЧЕМЙЮЙЧБАФУС Ч 5. 10 ТБЪ.
тБЪНЕТЩ РЕТЕДБЮЙ, РПМХЮЕООЩЕ РП РТЕДМПЦЕООЩН ЪБЧЙУЙНПУФСН, УПЗМБУХАФУС У ДБООЩНЙ ЛБФБМПЗПЧ ЙОПУФТБООЩИ ЖЙТН. рБТБНЕФТЩ ЪБГЕРМЕОЙС ЧЩВЙТБАФ У ХЮЕФПН РПДБФМЙЧПУФЙ ЪЧЕОШЕЧ.
дМС ХРТПЭЕОЙС ТБУЮЕФПЧ РТЙНЕОСАФ ХРТПЭЕООЩЕ ЪБЧЙУЙНПУФЙ, РТПЧЕТЕООЩЕ ЬЛУРЕТЙНЕОФБНЙ. пОЙ УРТБЧЕДМЙЧЩ ФПМШЛП ДМС ЬЧПМШЧЕОФОЩИ ЪХВЮБФЩИ ЛПМЕУ, ОБТЕЪБООЩИ УФБОДБТФОЩН ЙОУФТХНЕОФПН У ЙУИПДОЩН ЛПОФХТПН, ЙНЕАЭЙН α=20њ, ЛПЬЖЖЙГЙЕОФ ЧЩУПФЩ h_a*=1, ЛПЬЖЖЙГЙЕОФ ТБДЙБМШОПЗП ЪБЪПТБ у* =0,25 (ЙМЙ у*=0,35 ДМС НПДХМС ДП 1 НН); ДМС РЕТЕДБФПЮОПЗП ЮЙУМБ Ч ПДОПК УФХРЕОЙ u=60. 320, Б ФБЛЦЕ ДМС ХЛБЪБООЩИ ОЙЦЕ УППФОПЫЕОЙК ТБЪНЕТПЧ Й ЖПТНЩ ДЕЖПТНБГЙЙ ЗЕОЕТБФПТБ ЧПМО.
нПДХМШ ЪБГЕРМЕОЙС ЧЩЮЙУМСЕФУС РП ЪБЧЙУЙНПУФЙ m=d/z Й ПЛТХЗМСЕФУС ДП УФБОДБТФОПЗП.
тБЪНЕТЩ ЪХВЮБФЩИ ЛПМЕУ ПРТЕДЕМСАФ РП ЪБЧЙУЙНПУФСН, БОБМПЗЙЮОЩН ЪБЧЙУЙНПУФСН ДМС ПВЩЮОПЗП ЪБГЕРМЕОЙС.
🌟 Видео
Штангензубомер ШЗН-18. Как измерить зуб шестерни?Скачать
Измерение радиального биения зубчатого венца цилиндрической шестерни.Скачать
Зубчатые передачиСкачать
Расчет 2 (3.2) открытой цилиндрической зубчатой передачиСкачать
КПД эвольвентного прямозубого зацепления. (Excel-калькулятор).Скачать
4 5 расчет зубчатого колесаСкачать
Длина общей нормали. Измерение и программа для расчетаСкачать
Нарезка косозубой шестерниСкачать
Выбираем степень точности шестерен и зубчатых колес.Обозначение на чертеже. ГОСТ 1643-81Скачать
Чертежи зубчатого колеса и зубчатой парыСкачать
Лекция 3.2 Расчет цилиндрических зубчатых передачСкачать
Лекция «Конические зубчатые передачи»Скачать
Поделиться или сохранить к себе:
Search for:
Вектор
Вектор ав плюс вектор ва равно
1150
Окружность
Как построить центр окружности с помощью только
1145
Вектор
Как находить угол между векторами в кубе
1143
Четырехугольники
В четырехугольнике авсд векторы ав и сд противоположные точка к середина сд прямая ак
1165

Полезное
📏 Математика и архитектура: от древних пирамид до современных небоскребов
1154
Смотрите также
Ящик тянут по земле по горизонтальной окружности длиной 60
Ящик тянут по земле по горизонтальной окружности длиной 40
Ящик тянут по земле по горизонтальной окружности диаметром 20
Ящик тянут по земле за веревку по горизонтальной окружности длиной
Ящик тянут по земле за веревку по горизонтальной окружности диаметром
Электрон равномерно движется по окружности в однородном магнитном поле
Электрон и протон ускоренные разностью потенциалов движутся по окружности
Шарик скатывается по желобу изогнутому в виде дуги окружности
О сайте | | © 2024 Курс школьной геометрии.
№ УИЕНЩ уИЕНБ рЕТЕДБФПЮОПЕ
ПФОПЫЕОЙЕ йОФЕТЧБМЩ ТБГЙПОБМШОЩИ РЕТЕДБФПЮОЩИ ПФОПЫЕОЙК лрд РЕТЕДБЮ У ПРПТБНЙ ЛБЮЕОЙС иБТБЛФЕТЙУФЙЛБ Й ПВМБУФЙ РТЙНЕОЕОЙС
1 рТЙ ω₃=0
3. 12,5 0,96. 0,99
2 рТЙ ω₄=0
7. 16 0,96. 0,99
3 рТЙ ω ₁=0
дП 1600 Й ВПМЕЕ
4 31,5. 1600 Й ВПМЕЕ
5 рТЙ ω ₃=0
125. 10 000
6 рТЙ ω ₃=ω
₆=0 16. 125 0,93. 0,97
7 рТЙ ω ₂=0
7,1. 71 пВЩЮОП 16. 63 0,7. 0,94