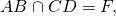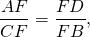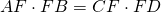в окружности проведены две пересекающиеся хорды. одна из них делится на отрезки 2 см и 6 см, а длина другой хорды 7 см. найдите отрезки второй хорды
Для решения рассмотрим рисунок (https://bit.ly/2WKEJvR).
Пусть длина отрезка СО = Х см, тогда величина отрезка ДО = (СД – СО) = (7 – Х) см.
Так как хорды АВ и СД пересекаются, то по свойству пересекающихся хорд, произведение длин отрезков одной хорды, образованных при пересечении, равно произведению отрезков другой хорды.
Тогда: АО * ВО = СО * ДО.
Х 2 – 7 * Х + 12 = 0.
Решим квадратное уравнение.
D = b 2 – 4 * a * c = (-7) 2 – 4 * 1 * 12 = 49 — 48 = 1.
x1 = (7 — √1) / (2 * 1) = (7 – 1) / 2 = 6 / 2 = 3.
x2 = (7 + √1) / (2 * 1) = (7 + 1) / 2 = 8 / 2 = 4.
Если СО = 3 см, то ДО = 4 см.
Если СО = 4 см, то ДО = 3 см.
Ответ: Длины отрезков второй хорды равны 3 см и 4 см.
Видео:№636. Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающиесяСкачать
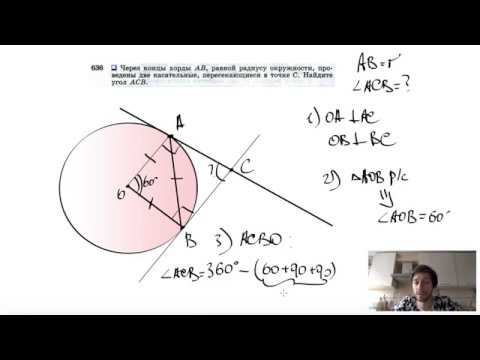
В окружности проведены две пересекающиеся хорды одна из хорд
Вопрос по геометрии:
В окружности проведены две пересекающиеся хорды. Одна из них делится на отрезки 2 см и 6 см, а длина другой 7 см. Найдите отрезки второй хорды. Даю 25 баллов!
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Рассмотрим вторую хорду. Она делится первой хордой в отношении: х и (7-х)
2*6=х(7-х)12=7х- х ² решаем квадратное уравнение.
х=4 см (первый корень)
х=3 см (второй корень)
Отрезки второй хорды : 4 и 3 (см) ; либо 3 и 4 (см)
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать
Хорды пересекаются
Если хорды пересекаются, как этот факт можно использовать при решении задач?
Теорема
(Свойство отрезков пересекающихся хорд (пропорциональность хорд окружности))
Произведения длин отрезков пересекающихся хорд, на которые эти хорды делятся точкой пересечения, есть число постоянное.
То есть, если хорды AB и CD пересекаются в точке F, то
AF ∙ FB=CF ∙ FD
Дано : окружность (O; R), AB и CD — хорды,
Доказать : AF ∙ FB=CF ∙ FD
1) Проведём отрезки BC и AD.
2) Рассмотрим треугольники AFD и CFB.
∠AFD=∠CFB (как вертикальные);
Следовательно, треугольники AFD и CFB подобны (по двум углам).
Из подобия треугольников следует пропорциональность соответствующих сторон:
то есть отрезки пересекающихся хорд пропорциональны.
По основному свойству пропорции:
Что и требовалось доказать .
При решении задач с пересекающимися хордами можно использовать не только вывод теоремы, но также полученный в ходе её доказательства факт, что пересекающиеся хорды образуют пары подобных треугольников.
Через точку M, лежащую внутри окружности, проведена хорда, которая делится точкой M на отрезки, длины которых равны 6 см и 16 см. Найти расстояние от точки M до центра окружности, если радиус окружности равен 14 см.
Дано : окружность (O; R), R=14 см, AB — хорда, M∈AB, AM=16 см, MB=6 см
Проведём через точку M диаметр CD.
По свойству отрезков пересекающихся хорд:
Пусть OM=x см (x>0). Так как радиус равен 14 см, то MD= (14-x) см, CM=(14+x) см.
Составим и решим уравнение:
Следовательно, расстояние от точки M до центра окружности равно 10 см.
В окружности проведены хорды AB и CD , пересекающиеся в точке F. Найти длину отрезка AC, если AF=6, DF=8, BD=20.
Дано : окружность (O; R), AB и CD — хорды,
В треугольниках AFC и BFD:
∠AFC=∠BFD (как вертикальные);
∠ACF=∠DBF (как вписанные углы, опирающиеся на одну хорду AD).
Следовательно, треугольники AFC и BFD подобны (по двум углам). Поэтому
📽️ Видео
№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать
теоренма об отрезках пересекающихся хордСкачать
Теорема о произведении отрезков пересекающихся хорд.Скачать
№672. Через точку А, лежащую вне окружности, проведены две секущие, одна из которых пересекаетСкачать
Всё про углы в окружности. Геометрия | МатематикаСкачать
Свойство пересекающихся хорд окружности. Геометрия 8-9 классСкачать
Теорема об отрезках хорд и секущихСкачать
Это Свойство Поможет Решить Задачи по Геометрии — Хорда, Окружность, Секущая (Геометрия)Скачать
Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать
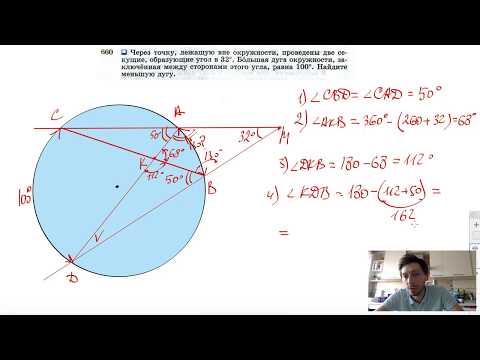
№660. Через точку, лежащую вне окружности, проведены две секущие, образующие угол в 32Скачать
11 класс, 41 урок, Две теоремы об отрезках, связанных с окружностьюСкачать
"Сложнее, чем кажется" — арабская олимпиадная задача, которую могли решить единицыСкачать
Свойство хорд в ОГЭ.Скачать
Пересекающиеся хорды окружности. Решишь задачу?Скачать
Свойство хорд, пересекающихся внутри окружностиСкачать
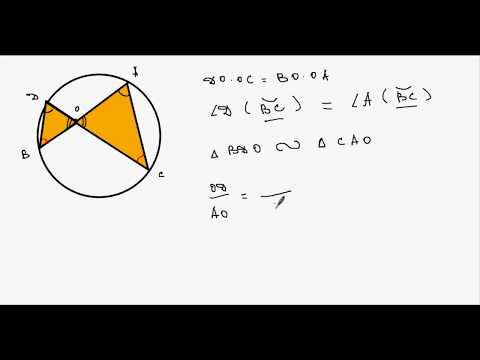
Окружность, диаметр, хорда геометрия 7 классСкачать
Докажите, что произведение отрезков одной хорды равно произведению отрезков другой хордыСкачать
Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать
