Которое из утверждений неверно центр окружности описанной около равностороннего

Ответ оставил Гость

1,2 верно, 3 нет, нужно написать 20 символов.

Если твой вопрос не раскрыт полностью, то попробуй воспользоваться поиском на сайте и найти другие ответы по предмету Геометрия.

Видео:2047 радиус окружности описанной около правильного треугольника равна 36 корней из 3Скачать

Верные, неверные утверждения. Геометрия

Верные, неверные утверждения. Задания для подготовки к ГВЭ по математике в 9 классе

Просмотр содержимого документа
«Верные, неверные утверждения. Геометрия»

Верные, неверные утверждения.

Укажите номера верных утверждений. Если их несколько, то записывайте их в порядке возрастания:
1) В равнобедренном треугольнике боковая сторона равна 10см, а основание 5см.
2) Одна из диагоналей параллелограмма со сторонами 7см и 6см равна 10см.
3) Существует треугольник со сторонами 11см, 10см, 21см
4) Треугольник со сторонами 10см, 5см, 8см — прямоугольный.

1. Выберите номера верных утверждений.

1). В треугольнике против большей стороны лежит больший угол.

2). Сумма односторонних углов при пересечении двух параллельных прямых секущей меньше 180°.

3). Если углы при основании треугольника равны, то треугольник равнобедренный.

2. Выберите номера неверных утверждений.

1). Если две противоположные стороны четырехугольника равны то этот четырехугольник — параллелограмм.

2). Диагонали ромба делят углы ромба пополам.

3). Трапеция равнобедренная, если её боковые стороны параллельны..

3. Выберите номера верных утверждений.

1). Серединный перпендикуляр к хорде проходит через центр окружности.

2). Точка касания двух окружностей лежит на линии центров.

3). Угол между двумя секущими, пересекающимися вне круга, равен полусумме дуг, высекаемых секущими на окружности.

4. Выберите номера верных утверждений.

1). Площадь треугольника равна произведению основания на высоту.

2). Площадь квадрата равна квадрату ее диагоналей.

3). Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

1. Выберите номера верных утверждений.

1). Если при пересечении двух прямых третьей образуются равные соответственные углы, то прямые параллельны.

2). Если гипотенуза одного прямоугольного треугольника равна гипотенузе другого прямоугольного треугольника, то такие треугольники равны.

3). Точка пересечения медиан треугольника- центр описанной окружности.

2. Выберите номера верных утверждений.

1). Диагонали ромба точкой пересечения делятся пополам.

2). В трапеции сумма углов при боковой стороне равна 90°.

3). Четырехугольник, у которого противоположные стороны попарно параллельны называется параллелограммом.

3. Выберите номера неверных утверждений.

1). Центр окружности, вписанной в треугольник,- это точка пересечения высот.

2). Угол, вершина которого лежит в центре окружности, называется вписанным.

3). Угол между касательной и хордой, проведенной из точки касания, равен половине угловой величины дуги,высекаемой на окружности этой хордой.

4. Выберите номера верных утверждений.

1). Площадь треугольника равна произведению периметра на радиус вписанной окружности.

2). Площадь прямоугольника равна половине произведения на синус угла между ними.

3). Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.

1. Выберите номера верных утверждений.

1). В треугольнике против меньшего угла лежит большая сторона.

2). При пересечении двух параллельных прямых секущей накрест лежащие углы равны.

3). В равнобедренном треугольнике углы при основании равны.

2. Выберите номера неверных утверждений.

1). В четырехугольнике сумма углов равна 360°.

2). Ромбом называют параллелограмм, у которого все стороны равны.

3). Если в трапецию вписана окружность, то трапеция равнобедренная.

3. Выберите номера верных утверждений.

1). Величина дуги окружности равна величине вписанного угла, на неё опирающегося.

2). Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.

3). Если к окружности из одной точки проведена касательная и секущая, то произведение всей секущей на её внешнюю часть равна квадрату касательной.

4. Выберите номера верных утверждений.

1). Площадь круга диаметром d равна .

2). Площадь параллелограмма равна половине произведения на высоту.

3). Если в подобные треугольники вписаны окружности, то отношение их радиусов равно коэффициенту подобия.

1. Выберите номера верных утверждений.

1). Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

2). Сумма двух сторон треугольника меньше третьей стороны.

3). Если две прямы параллельны третьей прямой, то они параллельны между собой.

2. Выберите номера верных утверждений.

1). Высота параллелограмма разбивает его на два равных треугольника.

2). В равнобедренной трапеции боковые стороны равны.

3). В ромбе противоположные углы равны.

3. Выберите номера неверных утверждений.

1). В ромбе диагонали являются биссектрисами углов.

2). Окружность симметрична относительно любого своего диаметра.

3). Гипотенуза прямоугольного треугольника равна радиусу окружности, описанной около этого треугольника.

4. Выберите номера верных утверждений.

1). Площадь треугольник равна отношению длин его сторон к радиусу описанной окружности.

2). Площадь трапеции равна произведению средней линии на высоту.

3). В прямоугольном треугольнике отношение катета к гипотенузе равно синусу угла, противолежащего этому катету.

Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Какие из следующих утверждений верны?

Математика | 5 — 9 классы

Какие из следующих утверждений верны?

1) Около любого правильного многоугольника можно описать не более одной окружности.

2) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.

3) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.

4) Около любого ромба можно описать окружность.

1) «Около лю­бо­го правильного мно­го­уголь­ни­ка можно опи­сать не более одной окружности.

»—верно, около лю­бо­го правильного мно­го­уголь­ни­ка можно опи­сать окружность, и при­том только одну.

2) «Центр окружности, опи­сан­ной около тре­уголь­ни­ка со сторонами, рав­ны­ми 3, 4, 5, на­хо­дит­ся на сто­ро­не этого треугольника.

» —верно, тре­уголь­ник с та­ки­ми сторонами яв­ля­ет­ся прямоугольным, таким образом, центр окруж­но­сти лежит на гипотенузе.

3) «Центром окружности, опи­сан­ной около квадрата, яв­ля­ет­ся точка пе­ре­се­че­ния его диагоналей.

» —верно, диа­го­на­ли квадрата точ­кой пересечения де­лят­ся пополам, таким образом, цен­тром окружности яв­ля­ет­ся точка пре­се­че­ния диагоналей.

4) «Около лю­бо­го ромба можно опи­сать окружность.

» —неверно, чтобы около четырёхуголь­ни­ка можно было опи­сать окруж­ность, не­об­хо­ди­мо, чтобы сумма про­ти­во­по­лож­ных углов четырёхуголь­ни­ка со­став­ля­ла 180°.

Это верно не для лю­бо­го ромба.

Видео:Радиус описанной окружностиСкачать

Квадрат описан около окружности радиуса 3 см найти радиус окружности, описанной около квадрата?

Квадрат описан около окружности радиуса 3 см найти радиус окружности, описанной около квадрата.

Видео:Задание 16 ОГЭ по математике. Окружность описана около равностороннего треугольника. Задача 2Скачать

1)Окружность вписанная в треугольник?

1)Окружность вписанная в треугольник?

Где находится центр такой окружности?

Какой отрезок будет являться её радиусом?

2)Окружность описанная около треугольника?

Где находится центр такой окружности?

Какой отрезок будет являться её радиусом?

3)Окружность описанная около прямоугольного треугольника?

Где находится центр такой окружности?

Чему равен её радиус?

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Какое из следующих утверждений верно?

Какое из следующих утверждений верно?

1) Диагонали ромба равны.

2) Отношение площадей подобных треугольников равно коэффициенту подобия.

3) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.

Видео:Построить описанную окружность (Задача 1)Скачать

Около квадрата со стороной 5(корень из 2) описана окружность?

Около квадрата со стороной 5(корень из 2) описана окружность.

Найдите сторону шестиугольника, описанного возле этой окружности.

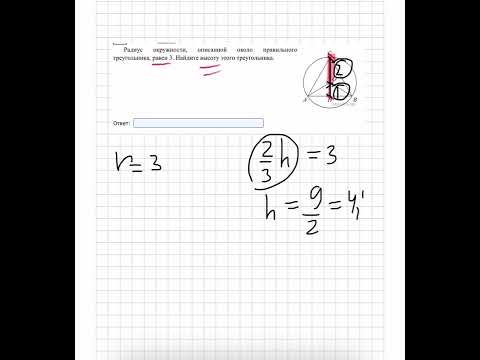
Видео:Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту треугольникаСкачать

Отмете верные утверждения 21?

Отмете верные утверждения 21.

1) Около всякого треугольника можно описать не более одной окружности.

2) В любой треугольник можно вписать не менее одной окружности.

3) Центром окружности, описанной около треугольника, является точка пересечения бис —

4) Центром окружности, вписанной в треугольник, является точка пересечения серединных

перпендикуляров к его сторонам.

22. 1) Около любого правильного многоугольника можно описать не более одной окружности.

2) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, нахо —

дится на стороне этого треугольника.

3) Центром окружности, описанной около квадрата, является точка пересечения его диаго —

4) Около любого ромба можно описать окружность.

23. 1) Окружность имеет бесконечно много центров симметрии.

2) Прямая не имеет осей сим —

3) Правильный пятиугольник имеет пять осей симметрии.

4) Квадрат не имеет центра сим —

24. 1) Правильный шестиугольник имеет шесть осей симметрии.

2) Прямая не имеет осей сим —

3) Центром симметрии ромба является точка пересечения его диагоналей.

4) Равнобедренный треугольник имеет три оси симметрии.

25. 1) Центром симметрии прямоугольника является точка пересечения диагоналей.

2) Центром симметрии ромба является точка пересечения его диагоналей

3) Правильный пятиугольник имеет пять осей симметрии.

4) Центром симметрии равнобедренной трапеции является точка пересечения ее диагона —

Видео:ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Сторона правильного треугольника, вписанного в некоторую окружность, равна 4 корня из 3 — ёх?

Сторона правильного треугольника, вписанного в некоторую окружность, равна 4 корня из 3 — ёх.

Найдите сторону правильного четырёхугольника, описанного около этой окружности.

Видео:Геометрия Найдите радиус окружности описанной около равнобедренного треугольника с основанием 16 смСкачать

ПОМОГИТЕ1?

Окружность описана около треугольника.

Верно ли, что вне точки окружности принадлежат плоскости треугольника?

Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Вокруг квадрата со стороной 6 см описана окружность?

Вокруг квадрата со стороной 6 см описана окружность.

Найдите : а) Радиус окружности.

Б)Сторону правильного треугольника, описанного около окружности.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Найдите радиус окружности, описанной около равностороннего треугольника, если его сторона равно 15 / корень3?

Найдите радиус окружности, описанной около равностороннего треугольника, если его сторона равно 15 / корень3.

Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Около квадрата со стороной a описана окружность, а около окружности описан правильный треугольник?

Около квадрата со стороной a описана окружность, а около окружности описан правильный треугольник.

Найдите сторону треугольника.

Видео:2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

Найдите радиус окружности, описанной около треугольника АВС, если центр окружности О удален от стороны АВ = 24см на расстояние 9см?

Найдите радиус окружности, описанной около треугольника АВС, если центр окружности О удален от стороны АВ = 24см на расстояние 9см.

Вы перешли к вопросу Какие из следующих утверждений верны?. Он относится к категории Математика, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Математика. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

1. 8, 5 / 3, 4 = 85 / 34 = 2, 5 17 — 2, 5 = 14, 5 14, 5 * 0, 6 = 8, 7 2. 5, 4 / 3, 6 = 54 / 36 = 1, 5 1, 5 — 1, 3 = 0, 2 0, 2 * 8, 5 = 1, 7 3. 1, 8 * 3, 4 = 6, 12 6, 12 + 0, 88 = 7 7 / 0, 35 = 700 / 35 = 20.

1200 : 3 = 400м — 1 / 8 400 * 8 = 3200 весь путь.

1. (0, 2х + 15у = 9, 8 * 2 = > (0, 4х + 30у = 19, 6 = > (2, 65х = 10, 6 = > (0, 75х — 10у = — 3 * 3 = > (2, 25х — 30у = — 9 = > (0, 4х + 30у = 19, 6 = > (х = 4 = > (х = 4 (0, 4 * 4 + 30у = 19, 6 = > (у = 0, 6 ( — типа фигурной скобки.

1)24х — 12х(в квадрате) + 120 — 60х = 0 — 48х + 120 = 0 — 48х = 120 х = — 2, 5 2)7х — 14 / 3 + 1 / 3 = 4х + 4 / 3 7х — 13 / 3 = 4х + 4 / 3 3х = 17 / 3 х = 1 8 / 9.

2354 * 47 = 110638 3187 * 32 = 101984 4823 * 26 = 125398.

Число 12 делится на 3 и 4 12 : 3 = 4 ; 12 : 4 = 3 — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — Число 12 делится на 6 и 12 12 : 6 = 2 ; 12 : 12 = 1 — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — ..

Кратное, значит делится на эти 2 числа без остатка 1)12 2)24 3) 36.

Пусть х кг огурцов в первой корзине , тогда х + 25 = 3х — 15 2х = 40 х = 20 кг в первой корзине 3 * 20 = 60 кг во второй корзине.

🎥 Видео

Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

5.5.5. Задачи на верность утверждений. Решение геометрических задач. Подготовка к ОГЭ по математикеСкачать

Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Разбор задания 13 ОГЭ по математикеСкачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Задание 19 (часть 1) | ОГЭ 2024 Математика | Анализ геометрических высказыванийСкачать

Задача на выбор неверных утвержденийСкачать