Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
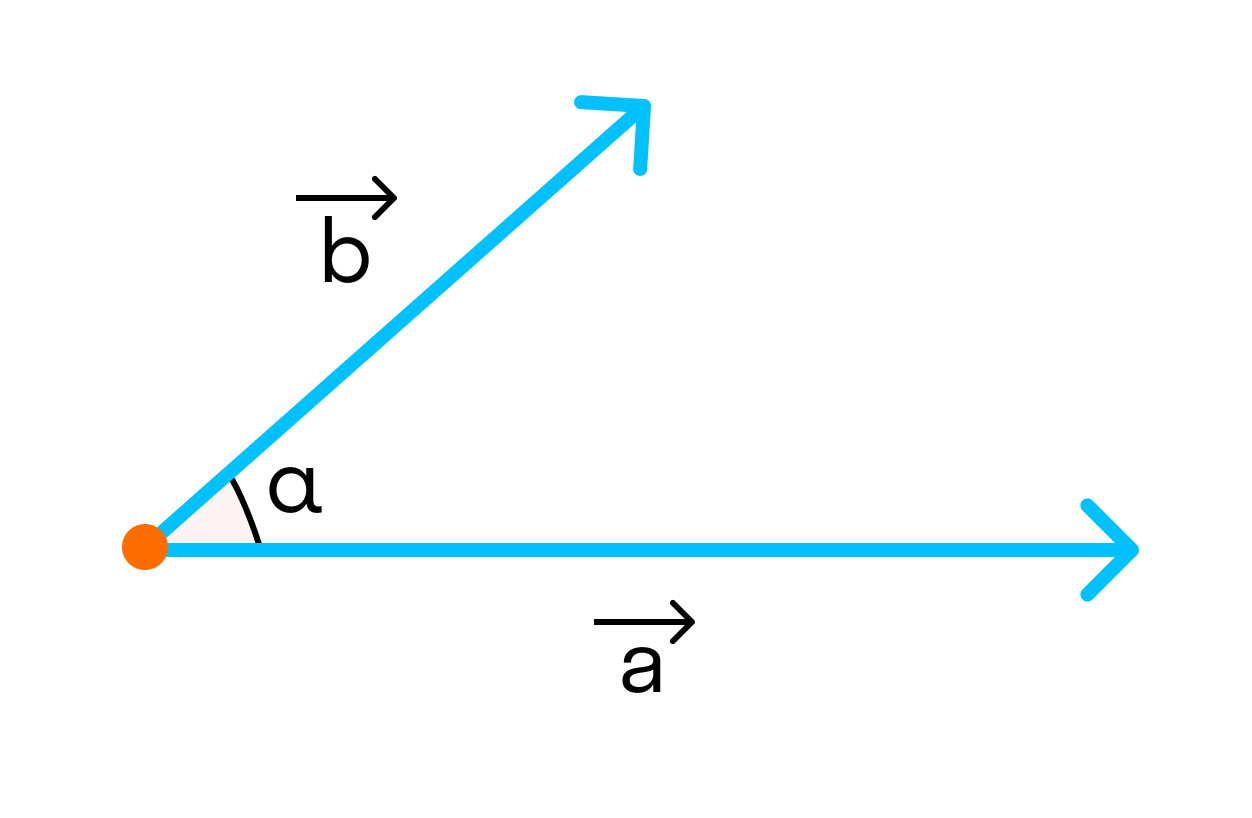
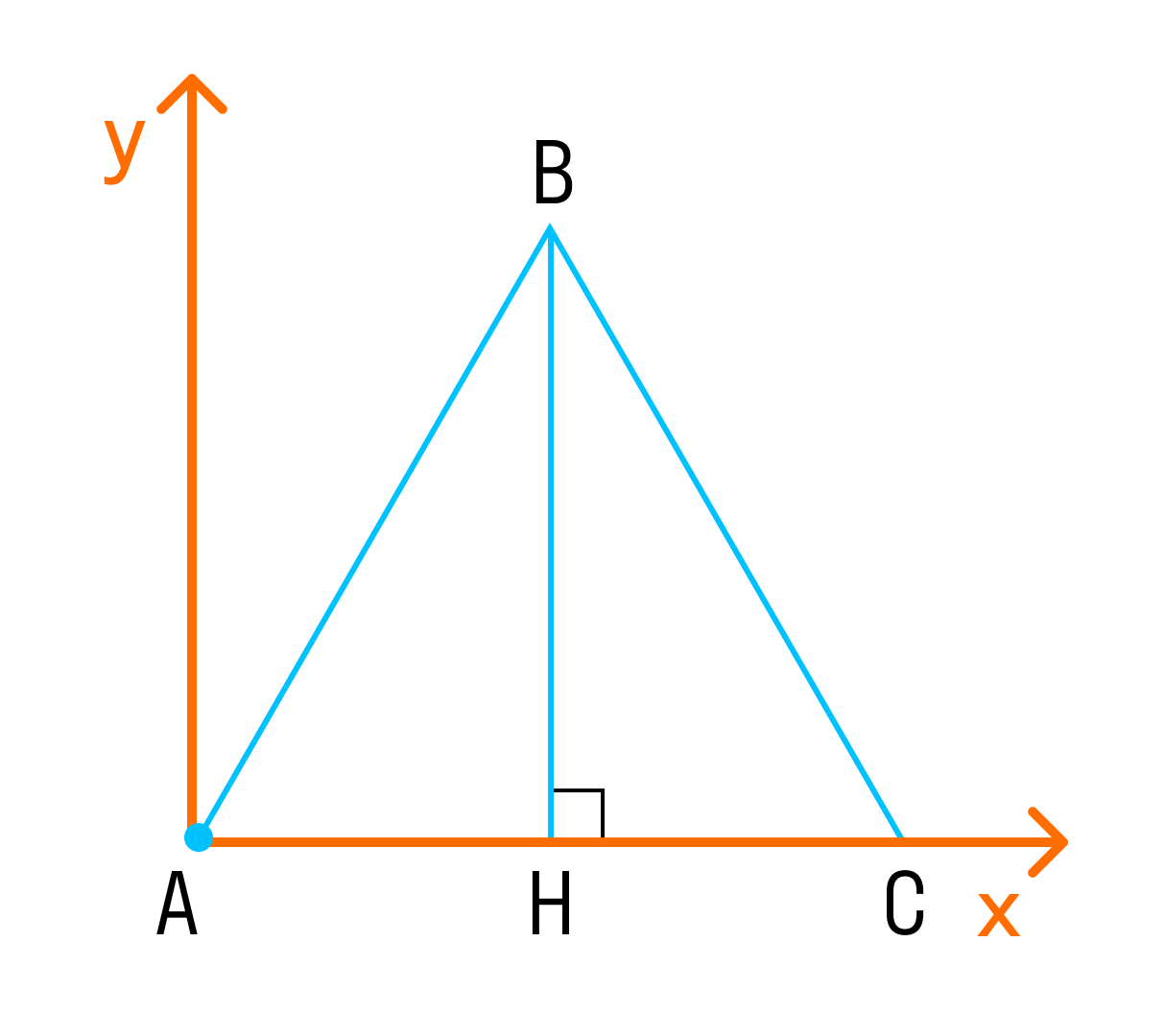
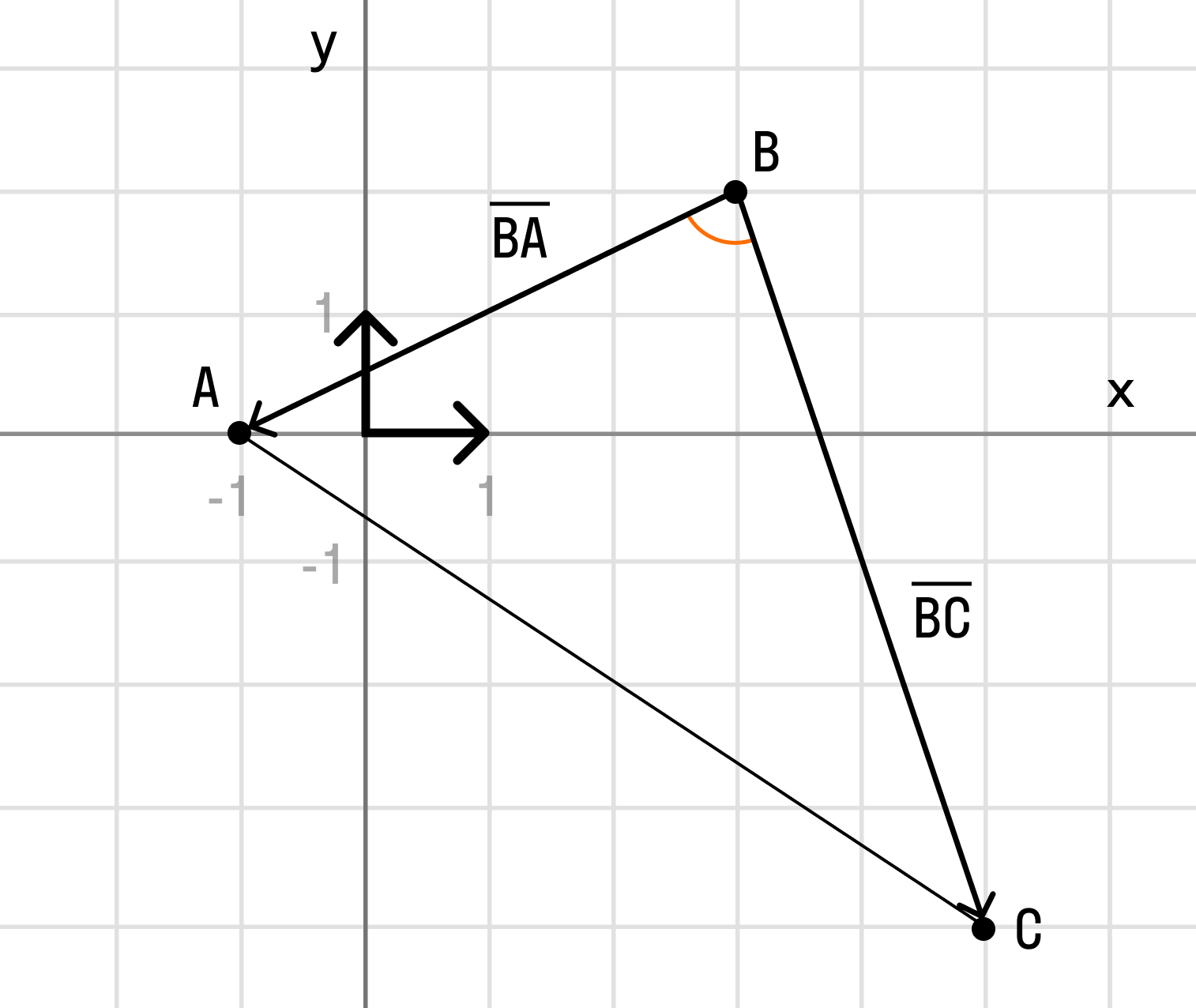
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →
Углом между векторами a → и b → называется угол между лучами О А и О В .
Полученный угол будем обозначать следующим образом: a → , b → ^
Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
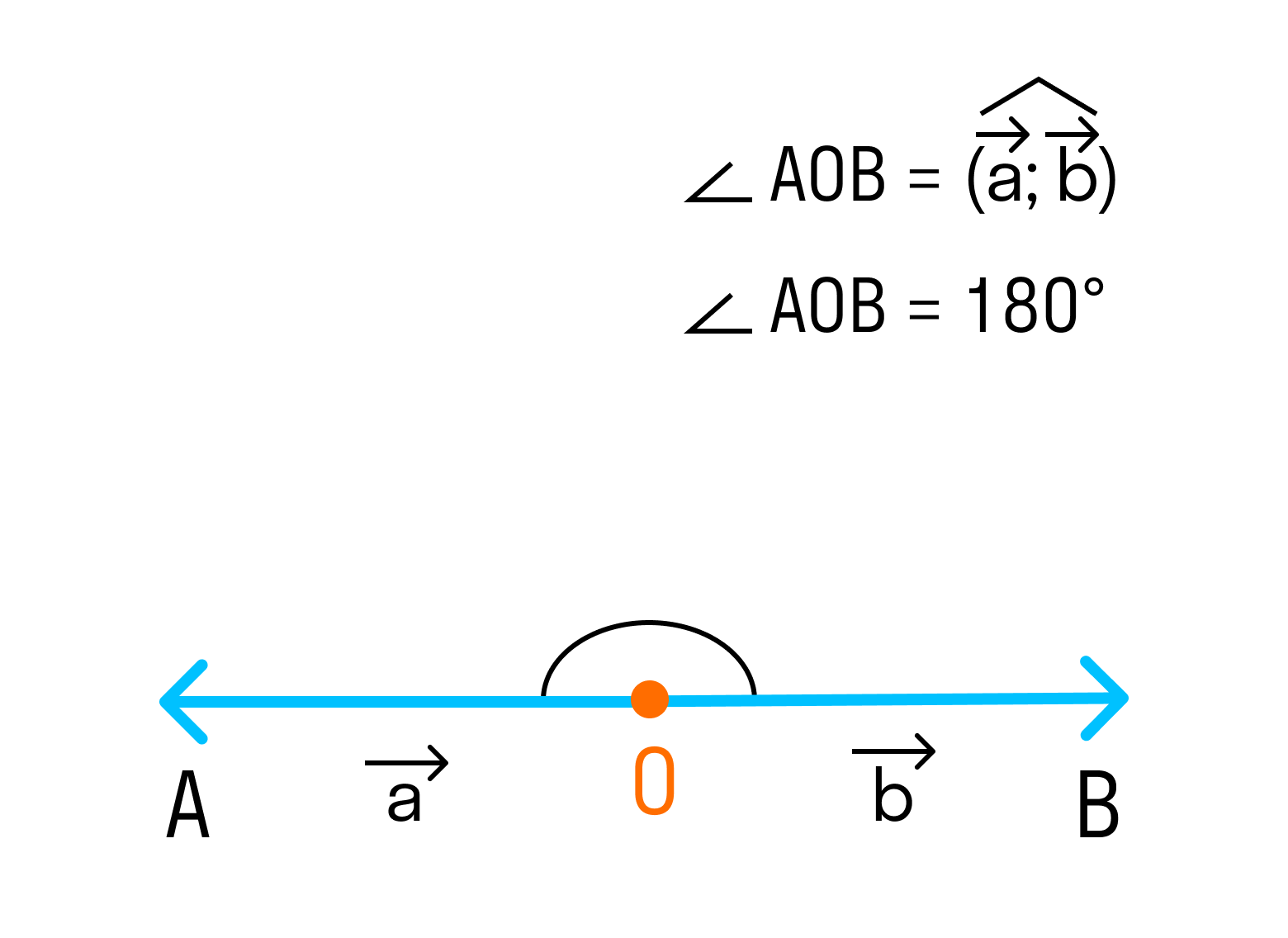
a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.
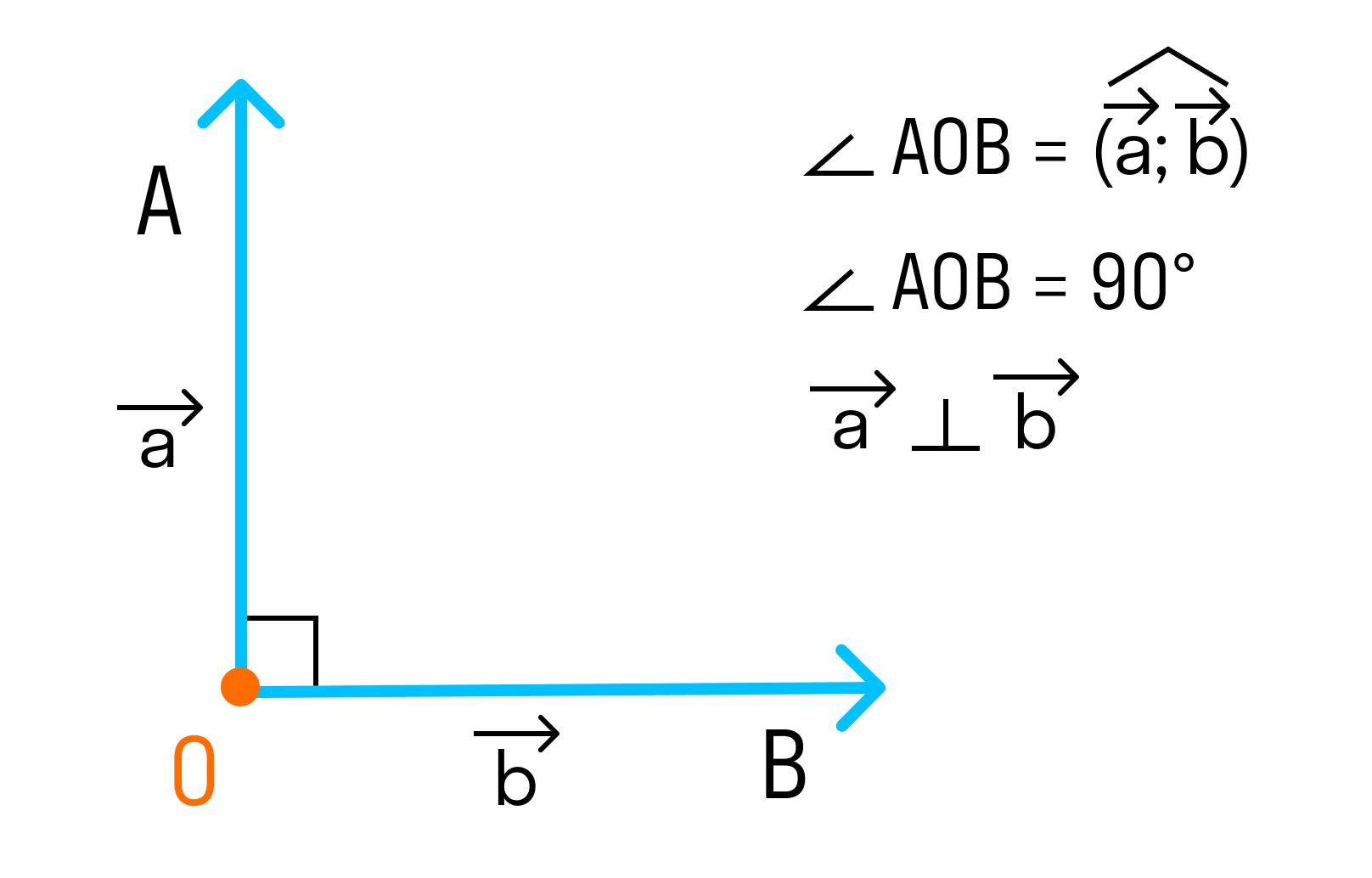
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.
Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.
- Нахождение угла между векторами
- Скалярное произведение векторов
- Основные определения
- Угол между векторами
- Скалярное произведение векторов
- Скалярное произведение в координатах
- Формулы скалярного произведения векторов заданных координатами
- Свойства скалярного произведения
- Примеры вычислений скалярного произведения
- Геометрия. 11 класс
- 🔍 Видео
Видео:Угол между векторами. 9 класс.Скачать

Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .
Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cos a → , b → ^ = a → , b → a → · b →
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно — 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = — 9 3 · 6 = — 1 2 ,
Теперь определим угол между векторами: a → , b → ^ = a r c cos ( — 1 2 ) = 3 π 4
Ответ: cos a → , b → ^ = — 1 2 , a → , b → ^ = 3 π 4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:
cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2
Исходные данные: векторы a → = ( 2 , 0 , — 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cos a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 2 2 + 0 2 + ( — 1 ) 2 · 1 2 + 2 2 + 3 2 = — 1 70 ⇒ a → , b → ^ = a r c cos ( — 1 70 ) = — a r c cos 1 70
- Также можно определить угол по формуле:
cos a → , b → ^ = ( a → , b → ) a → · b → ,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( — 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 = — 1 cos a → , b → ^ = a → , b → ^ a → · b → = — 1 5 · 14 = — 1 70 ⇒ a → , b → ^ = — a r c cos 1 70
Ответ: a → , b → ^ = — a r c cos 1 70
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , — 1 ) , B ( 3 , 2 ) , C ( 7 , — 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .
Решение
Найдем координаты векторов по координатам заданных точек A C → = ( 7 — 2 , — 2 — ( — 1 ) ) = ( 5 , — 1 ) B C → = ( 7 — 3 , — 2 — 2 ) = ( 4 , — 4 )
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( — 1 ) · ( — 4 ) 5 2 + ( — 1 ) 2 · 4 2 + ( — 4 ) 2 = 24 26 · 32 = 3 13
Ответ: cos A C → , B C → ^ = 3 13
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:
A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos ( ∠ A O B ) ,
b → — a → 2 = a → + b → — 2 · a → · b → · cos ( a → , b → ) ^
и отсюда выведем формулу косинуса угла:
cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 — b → — a → 2 a → · b →
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
Видео:Нахождение угла между векторами через координаты. 9 класс.Скачать

Скалярное произведение векторов
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Угол между векторами | МатематикаСкачать

Основные определения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
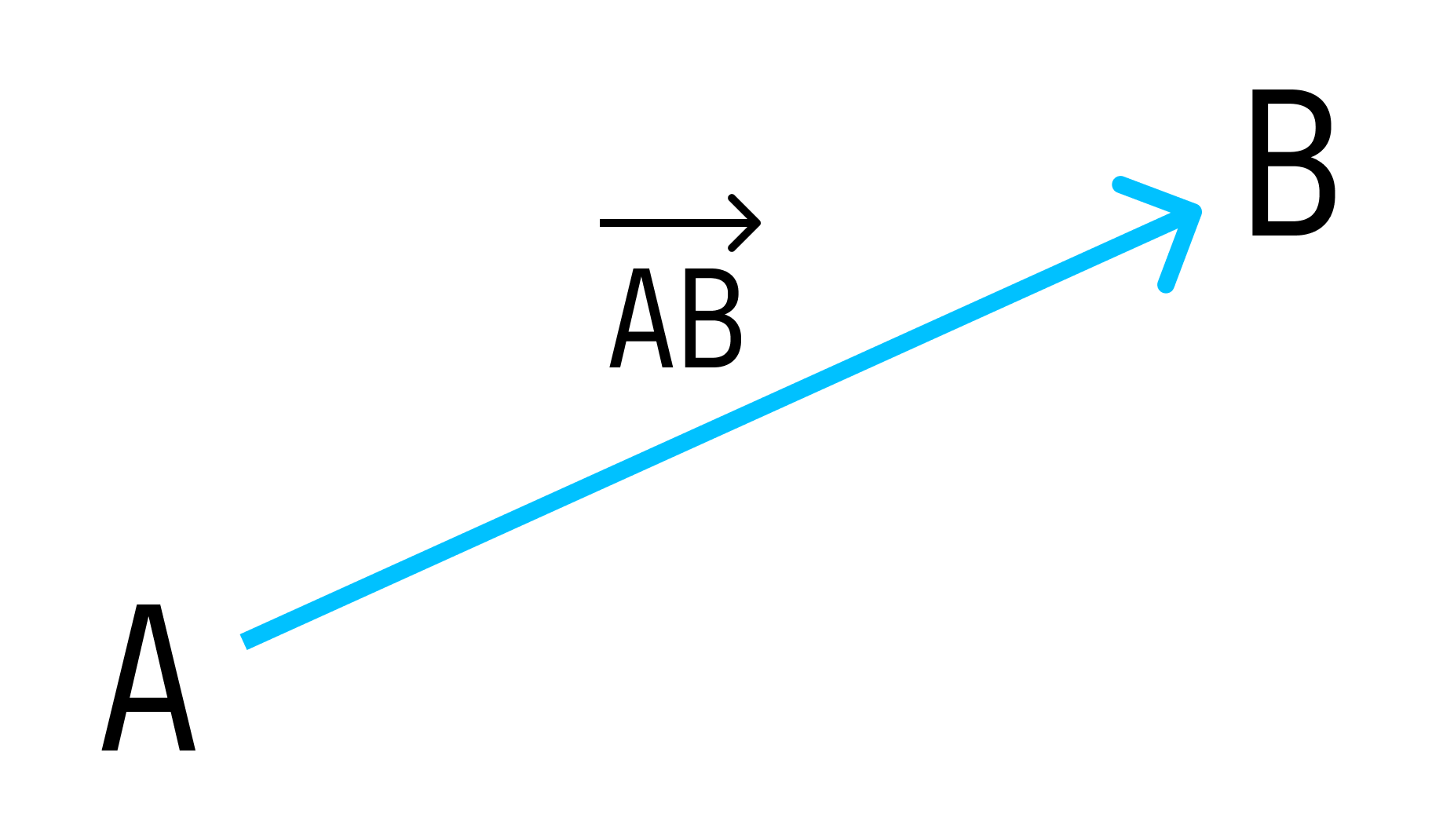
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.
Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.
Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.
Видео:Геометрия 9 класс (Урок№18 - Угол между векторами. Скалярное произведение векторов.)Скачать

Угол между векторами
Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства: 0°=
2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.
3. Если векторы направлены в разные стороны, тогда угол между ними 180°.
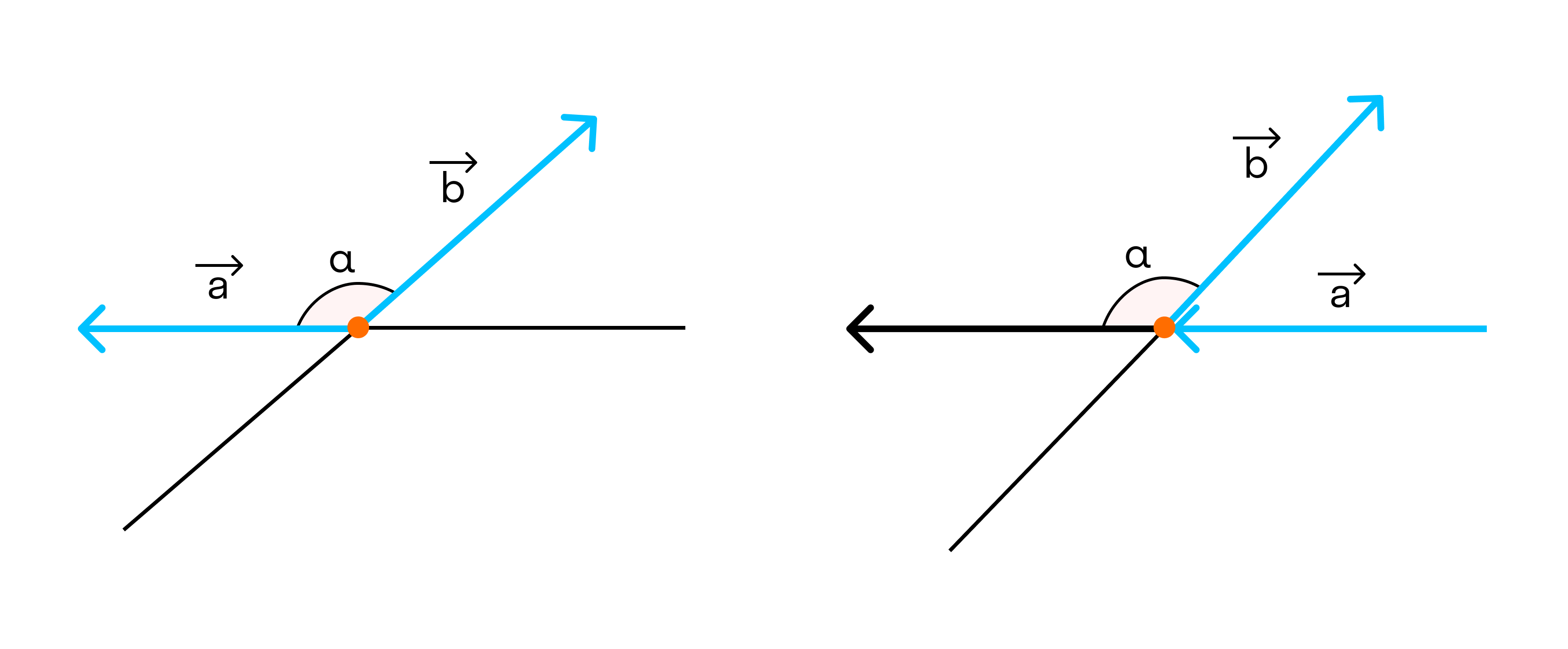
Также векторы могут образовывать тупой угол. Это выглядит так:
Видео:Как находить угол между векторамиСкачать

Скалярное произведение векторов
Определение скалярного произведения можно сформулировать двумя способами:
Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.
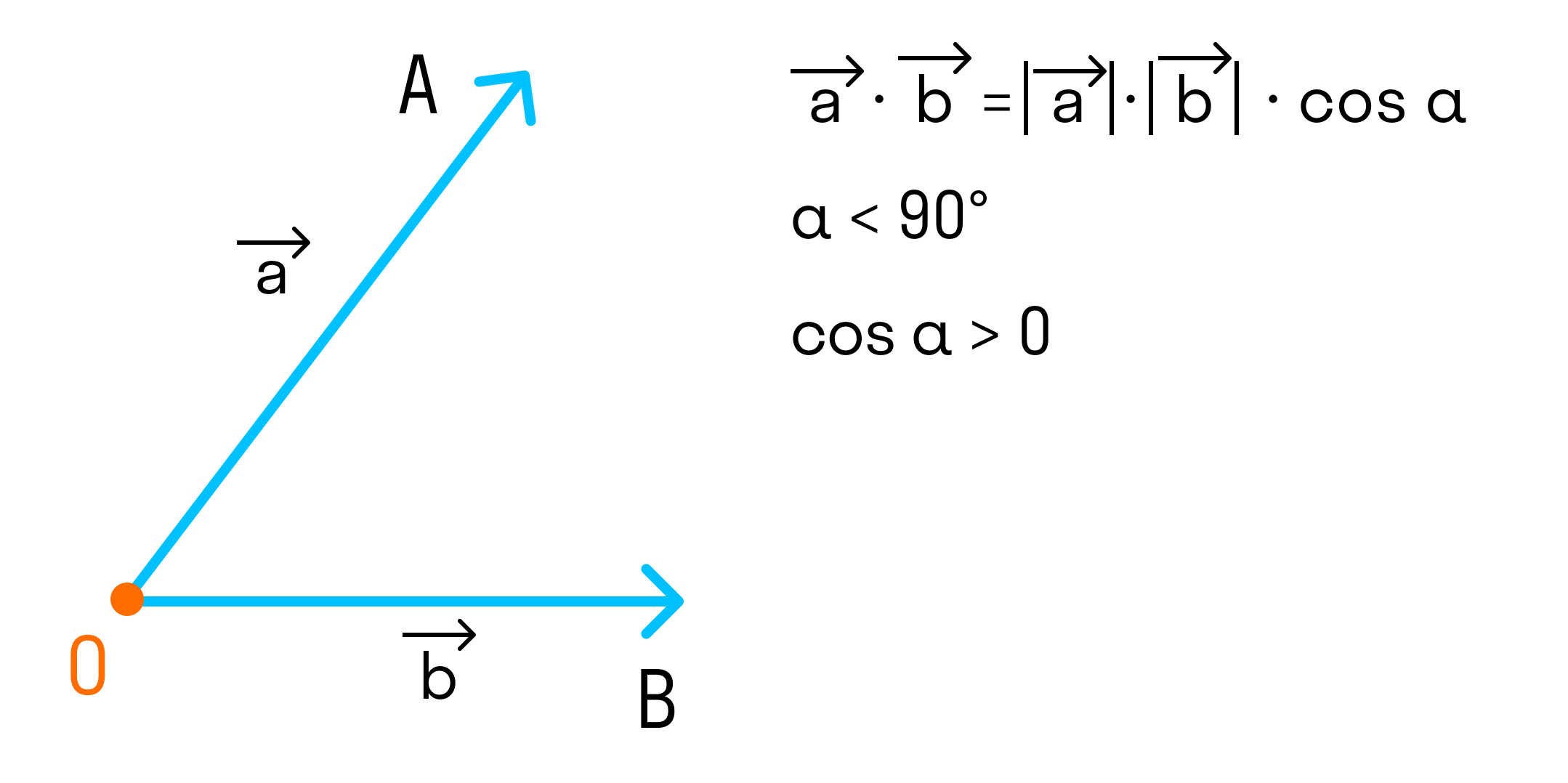
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:
→a * →b = →|a| * →|b| * cosα
Что важно запомнить про геометрическую интерпретацию скалярного произведения:
- Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, то есть cosα > 0.
- Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как cosα
Видео:Косинус угла между векторами. Коллинеарность векторовСкачать

Скалярное произведение в координатах
Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.
Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов →a и →b.
То есть для векторов →a = (ax, ay), →b = (bx, by) на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид: (→a, →b) = ax*bx + ay*by
А для векторов →a = (ax, ay, az), →b = (bx, by, bz) в трехмерном пространстве скалярное произведение в координатах находится так: (→a, →b) = ax*bx + ay*by + az*bz
Докажем это определение:
Сначала докажем равенства
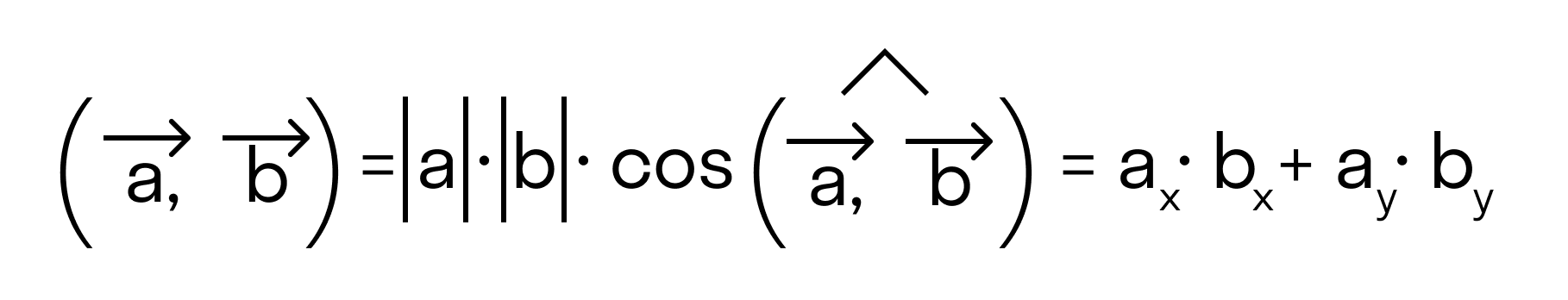
для векторов →a = (ax, ay), →b = (bx, by) на плоскости, заданных в прямоугольной декартовой системе координат.
Отложим от начала координат (точка О) векторы →OB = →b = (bx, by) и →OA = →a = (ax, ay)
Тогда, →AB = →OB — →OA = →b — →a = (bx — ax, by — ay)
Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов можно записать:
то последнее равенство можно переписать так:
а по первому определению скалярного произведения имеем
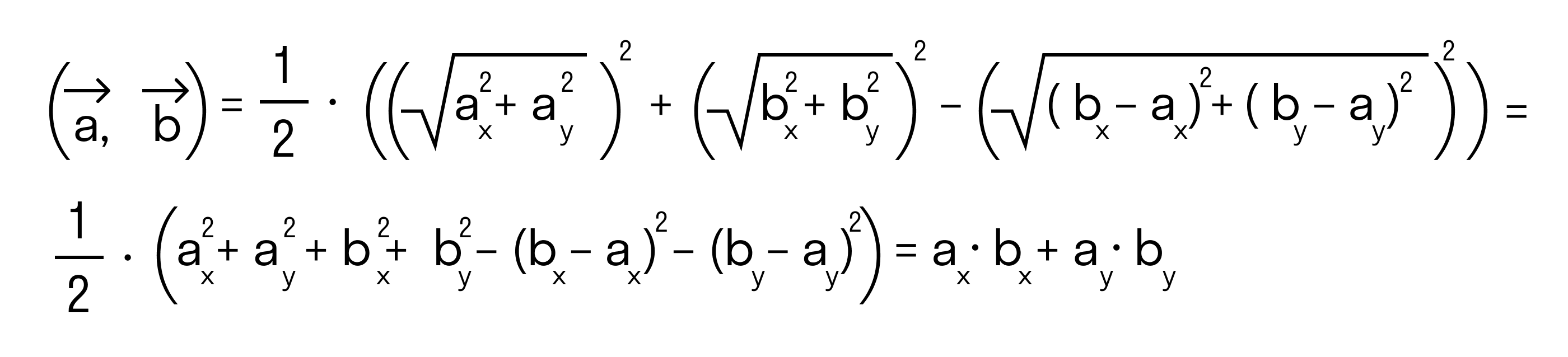



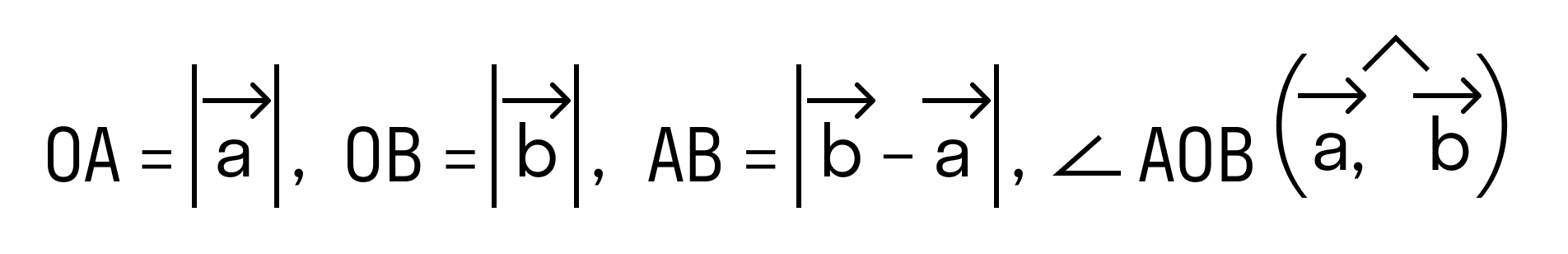
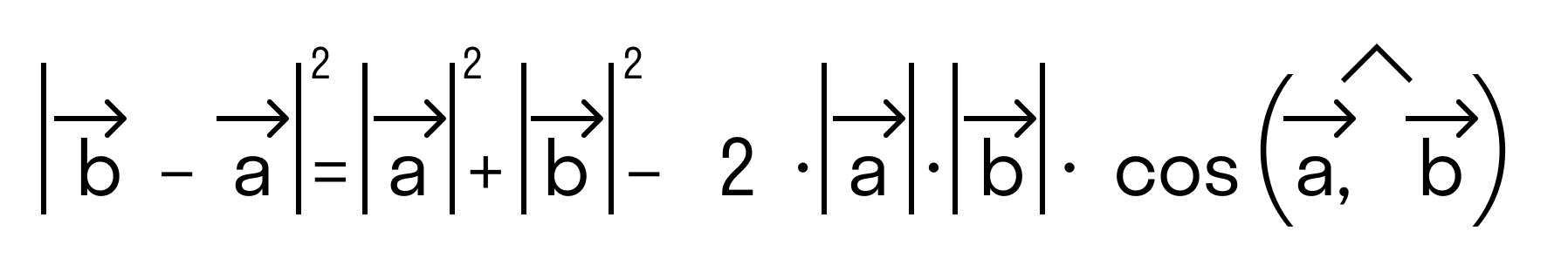
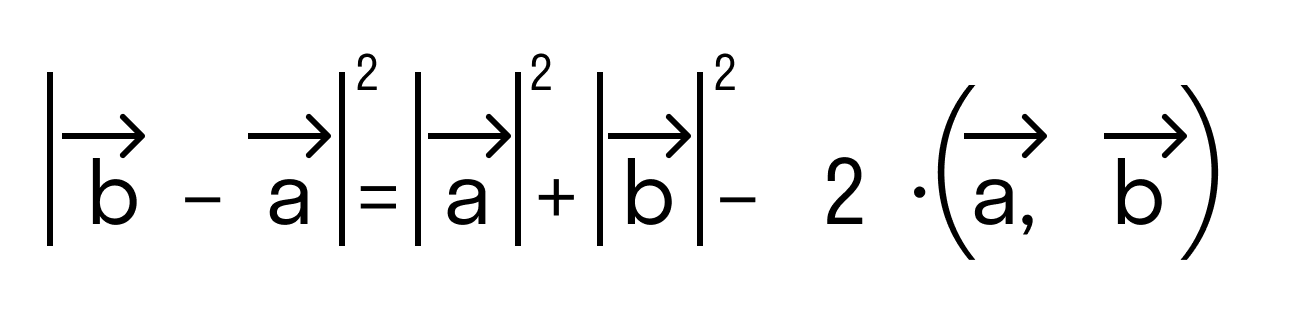
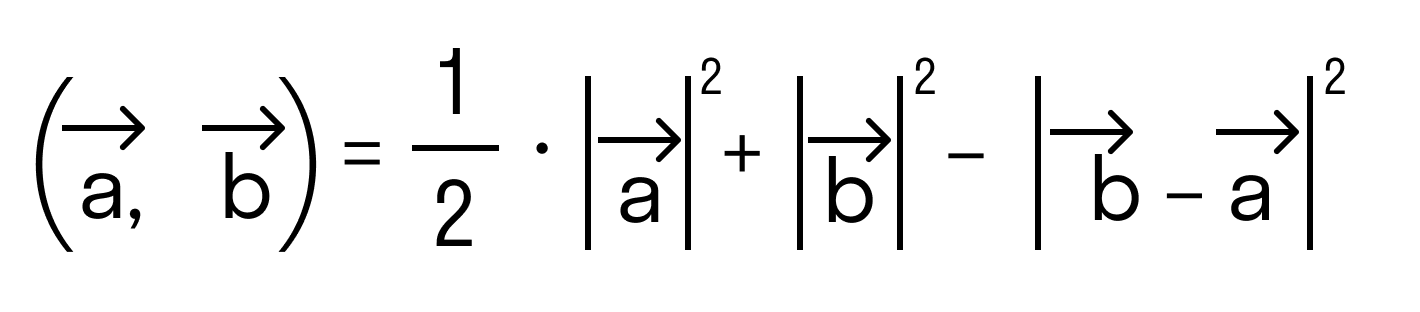


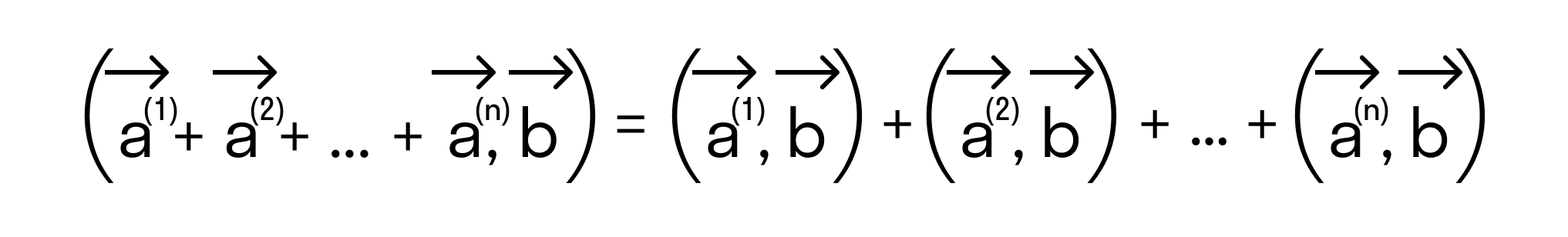
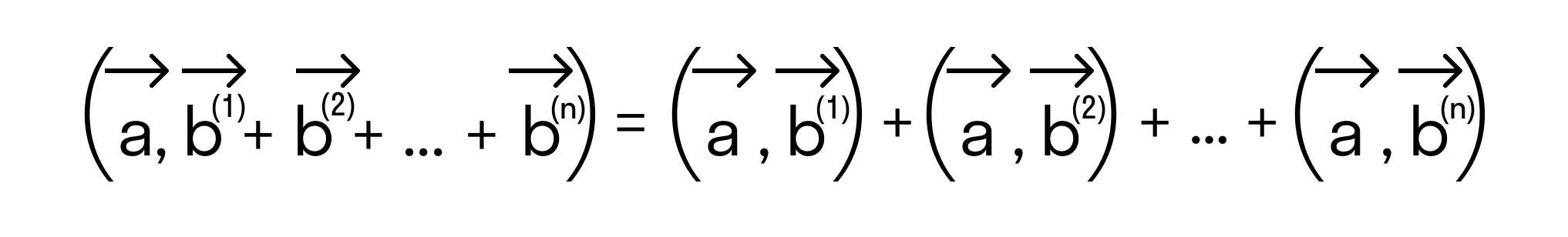
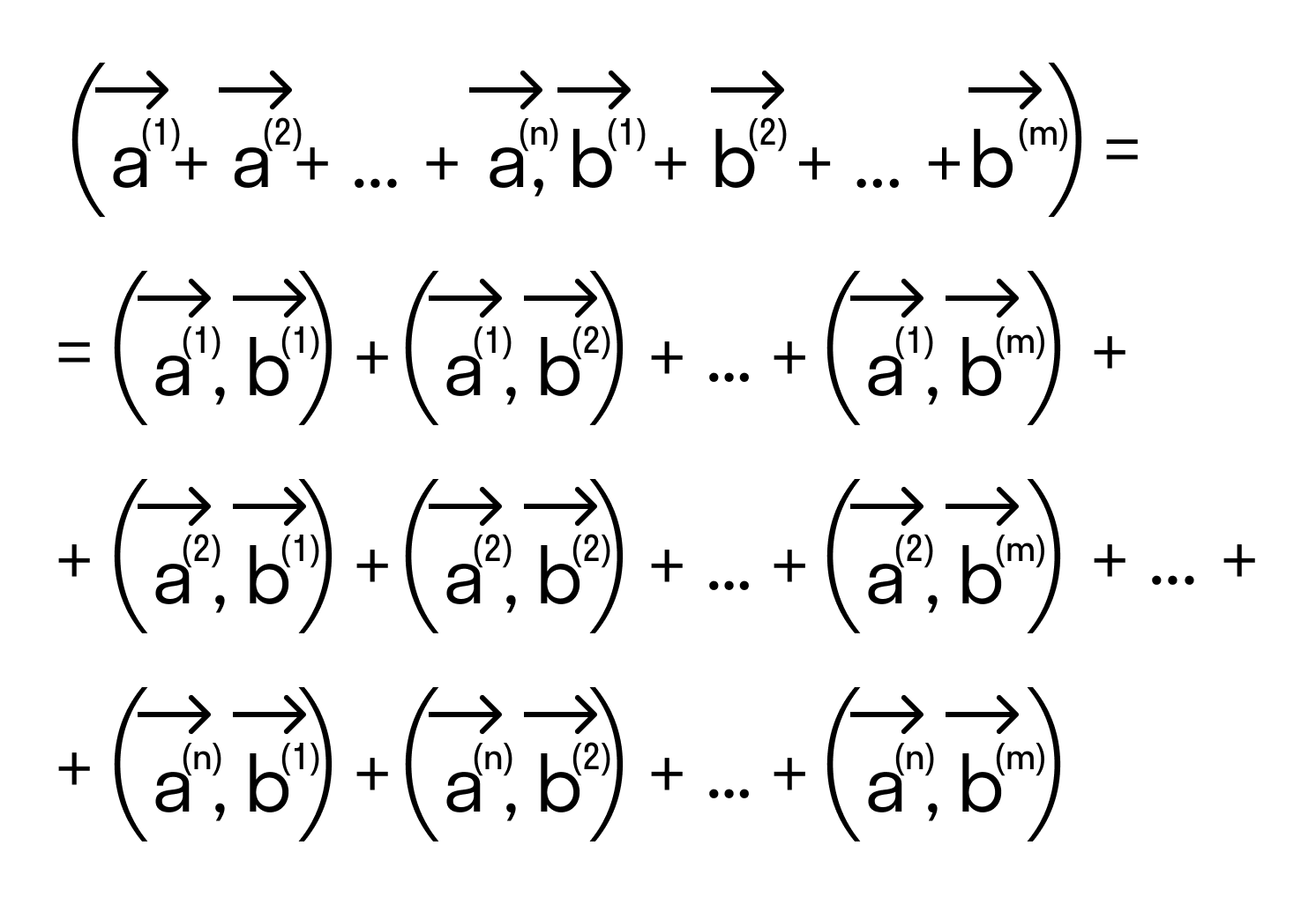

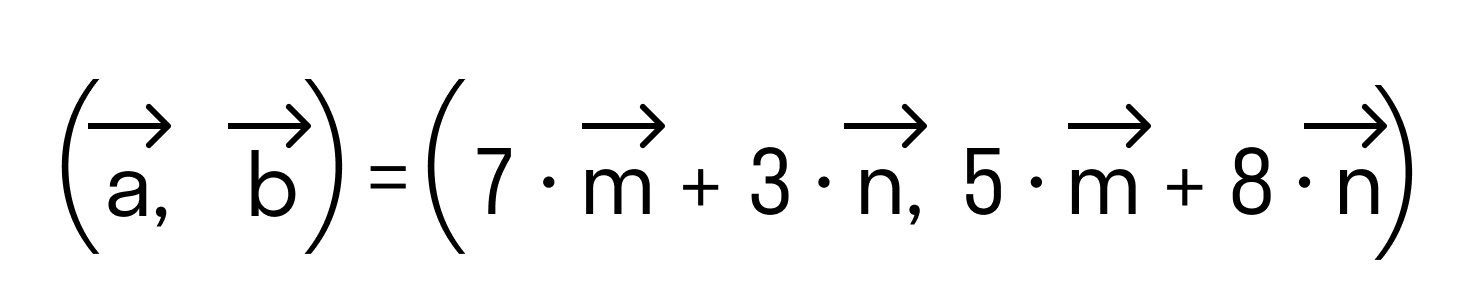
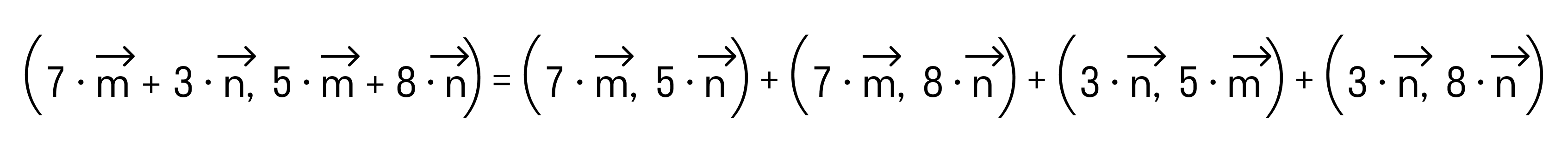
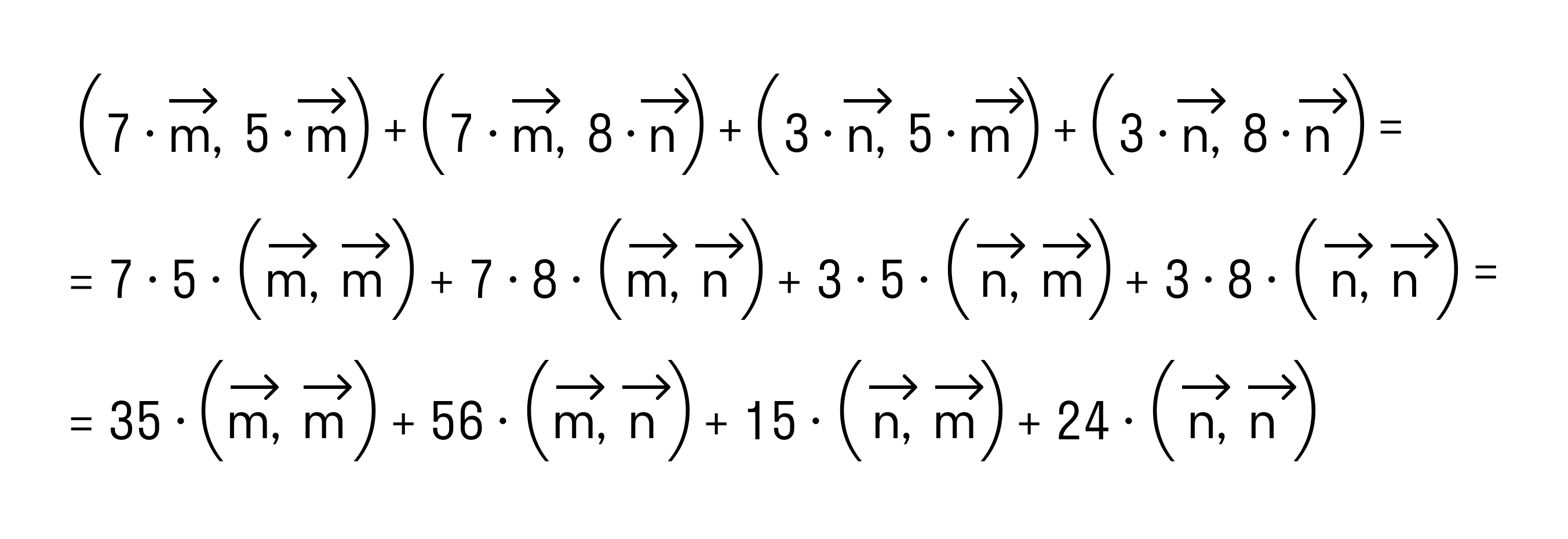
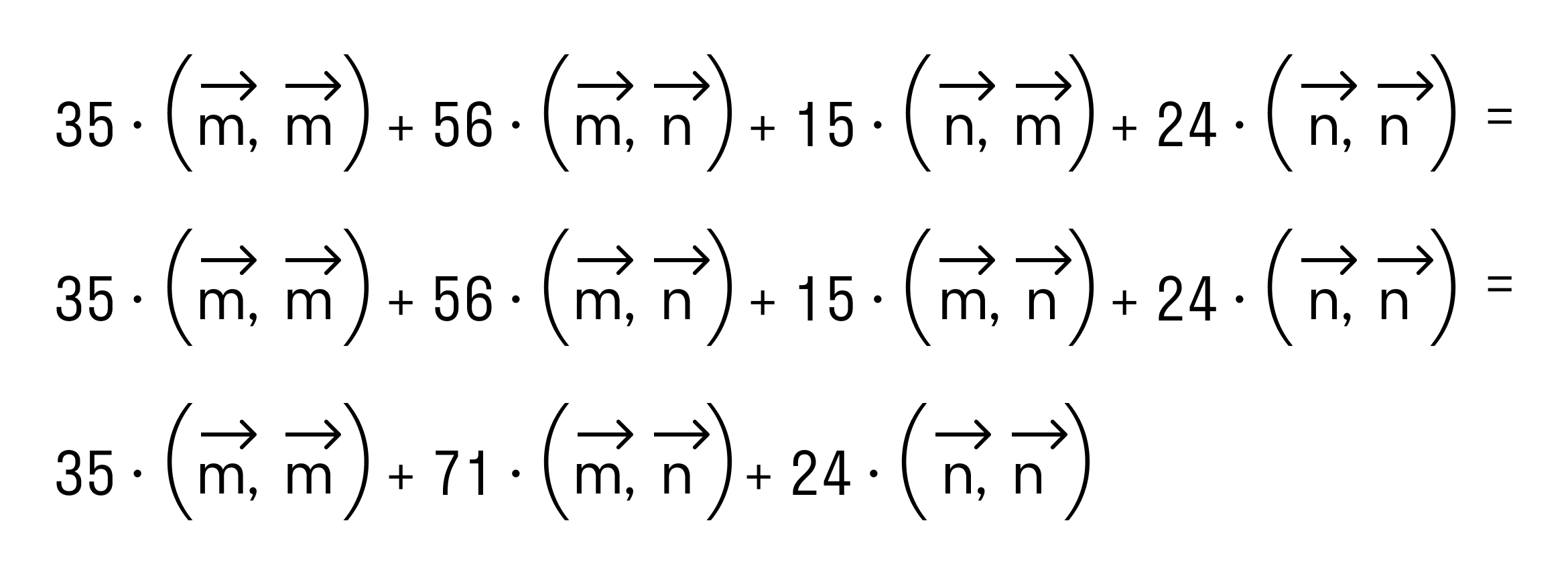
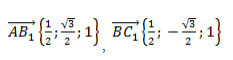
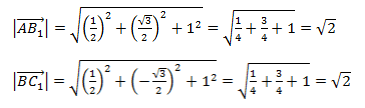
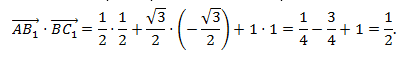
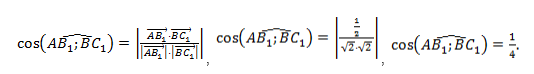
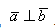
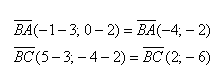
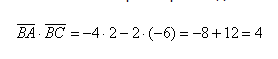
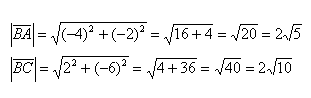
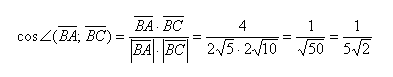
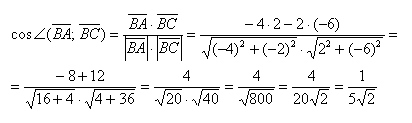
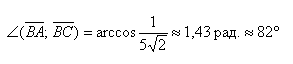







 равен квадрату его длины.
равен квадрату его длины. 
 и
и 



 , заданными в ортонормированном базисе
, заданными в ортонормированном базисе  , выражается формулой:
, выражается формулой: 
 и любого числа k справедливы равенства:
и любого числа k справедливы равенства: причем
причем  при
при 
 (переместительный закон).
(переместительный закон). (распределительный закон).
(распределительный закон). (сочетательный закон).
(сочетательный закон).
 прямоугольный параллелепипед, где
прямоугольный параллелепипед, где  . Найти
. Найти  и
и  .
.
 Только для этого необходимо знать координаты направляющих векторов прямых. В данном случае, для прямой BD направляющим может является вектор BD , а для прямой
Только для этого необходимо знать координаты направляющих векторов прямых. В данном случае, для прямой BD направляющим может является вектор BD , а для прямой 






 .
.