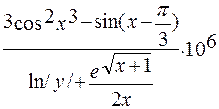В ML существует большое количество элементарных математических функций для выполнения действий с числами: тригонометрические, степенные, логарифмические, экспоненциальные и функции округления. Каждая функция обладает именем и списком аргументов, которые задаются в круглых скобках и, если их несколько, перечисляются через запятую.
Существуют встроенные тригонометрические и гиперболические функции: sin(x), cos(x), tan(x), cot(x), asin(x), acos(x), atan(x), acot(x), sinh(x) и т.д. Аргументы этих функций (в следующих версиях, начиная с версии 7.0) могут задаваться в радианах и градусах. У функций в градусной мере после названия добавляется буква d. sin(x) – аргумент в радианах, а sind(x) – аргумент в градусах.
Некоторые часто используемые математические функции:
· exp(x)–экспонента числа x;
· log(x)– натуральный логарифм;
· log10(x)– десятичный логарифм;
· sqrt(x)– квадратный корень;
· abs(x)– абсолютное значение x;
· mod(x, y)– остаток от целочисленного деления с учетом знака;
· rem(x, y)– остаток от целочисленного деления без учета знака;
· real(z)– вещественная часть комплексного числа;
· imag(z)– мнимая часть комплексного числа;
· round(x)– округление до ближайшего целого.
Более полный список основных математических функций MatLab:
| sqrt(x) | вычисление квадратного корня |
| exp(x) | возведение в степень числа e |
| pow2(x) | возведение в степень числа 2 |
| log(x) | вычисление натурального логарифма |
| log10(x) | вычисление десятичного логарифма |
| log2(x) | вычисление логарифма по основанию 2 |
| sin(x) | синус угла x, заданного в радианах |
| cos(x) | косинус угла x, заданного в радианах |
| tan(x) | тангенс угла x, заданного в радианах |
| cot(x) | котангенс угла x, заданного в радианах |
| asin(x) | арксинус |
| acos(x) | арккосинус |
| atan(x) | арктангенс |
| pi | число пи |
| round(x) | округление до ближайшего целого |
| fix(x) | усечение дробной части числа |
| floor(x) | округление до меньшего целого |
| ceil(x) | округление до большего целого |
| mod(x,y) | остаток от деления с учётом знака |
| sign(x) | знак числа |
| factor(x) | разложение числа на простые множители |
| isprime(x) | истинно, если число простое |
| rand | генерация псевдослучайного числа с равномерным законом распределения |
| randn | генерация псевдослучайного числа с нормальным законом распределения |
| abs(x) | вычисление модуля числа |
С использованием вышеупомянутых функций, записать и сосчитать значение арифметического выражения:
Вычислить: res=
Составление арифметического выражения лучше всего начинать с расстановки основных скобок выражения. Причем открытую скобку следует сразу закрывать и продолжать набор формулы внутри скобок. В этом случае число открывающих скобок будет равно числу закрывающих, и вероятность ошибки будет минимальной.
Если в выражении многократно встречаются одинаковые фрагменты, то их целесообразно вычислять 1 раз и результат помещать в отдельные переменные. Это позволяет избежать одинаковых вычислений и тем самым оптимизирует вычисления.
res=(3*cos(x^3)^2-sin(x-pi/3))/(log(abs(y))+exp (sqrt (x+1))/(2*x))*1E6
Для эффективной работы с большими наборами данных или при необходимости многократных вычислений рассмотренных средств недостаточно. В ML существует возможность записать последовательность команд в файл, сохранить его, дать ему имя и выполнить, набрав в командной строке имя файла. Это можно сделать во встроенном редакторе системы. Такие файлы называются файлами-сценариями или скрипт-файлами. При сохранении они автоматически получают расширение системы – m.
Файлы-программы (их называют скриптами или сценариями) являются самым простым типом m-файлов. Script-файл состоит из последовательности команд, не содержит заголовка, а также входных и выходных параметров. Все объекты, используемые внутри script-файла, считаются глобальными. Если в рабочем пространстве есть данные, то внутри script-файла их можно использовать, а по окончании его выполнения использовать данные, созданные с его помощью. Такие файлы используются для автоматизации выполнения большого набора инструкций. Их текст набирают в окне встроенного редактора ML.
Для выполнения файла-программы достаточно в командной строке указать имя этого скрипта. Перед запуском программы на выполнение необходимо установить нужный каталог в качестве текущего. Запуск файла на выполнение можно осуществить двумя способами: из окна редактора и из командного окна.
Для запуска программы на выполнение из окна редактора надо выбрать пункт меню Debug, Run или нажать функциональную клавишу F5, или выбрать соответствующую пиктограмму на панели инструментов. Выполнить программу, уже сохраненную на диске, можно из командного окна ML, просто набрав имя файла без расширения.
Дата добавления: 2016-04-02 ; просмотров: 5836 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
- Косинус между векторами matlab
- Syntax
- Description
- Examples
- Plot Cosine Function
- Cosine of Vector of Complex Angles
- Input Arguments
- X — Input angle in radians scalar | vector | matrix | multidimensional array
- Output Arguments
- Y — Cosine of input angle scalar | vector | matrix | multidimensional array
- More About
- Cosine Function
- Extended Capabilities
- Tall Arrays Calculate with arrays that have more rows than fit in memory.
- C/C++ Code Generation Generate C and C++ code using MATLAB® Coder™.
- GPU Code Generation Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.
- Thread-Based Environment Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool .
- GPU Arrays Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
- Distributed Arrays Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
- Угол между двумя векторами matlab
- Художественные модели для рисования — эталонные изображения для рисования фигур (NON-NUDE SERIES DLDS # 6) в Ultra HD 4K
- 📽️ Видео
Видео:Угол между векторами. 9 класс.Скачать

Косинус между векторами matlab
Cosine of argument in radians
Видео:Угол между векторами | МатематикаСкачать

Syntax
Видео:Косинус угла между векторами. Коллинеарность векторовСкачать

Description
Y = cos( X ) returns the cosine for each element of X . The cos function operates element-wise on arrays. The function accepts both real and complex inputs.
For real values of X , cos(X) returns real values in the interval [-1, 1].
For complex values of X , cos(X) returns complex values.
Видео:Нахождение угла между векторами через координаты. 9 класс.Скачать

Examples
Plot Cosine Function
Plot the cosine function over the domain — π ≤ x ≤ π .
Cosine of Vector of Complex Angles
Calculate the cosine of the complex angles in vector x .
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Input Arguments
X — Input angle in radians
scalar | vector | matrix | multidimensional array
Input angle in radians, specified as a scalar, vector, matrix, or multidimensional array.
Data Types: single | double
Complex Number Support: Yes
Видео:Как находить угол между векторамиСкачать

Output Arguments
Y — Cosine of input angle
scalar | vector | matrix | multidimensional array
Cosine of input angle, returned as a real-valued or complex-valued scalar, vector, matrix or multidimensional array.
Видео:Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

More About
Cosine Function
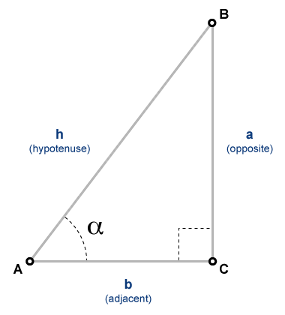
The cosine of an angle, α, defined with reference to a right angled triangle is
cos ( α ) = adjacent side hypotenuse = b h .
The cosine of a complex argument, α, is
cos ( α ) = e i α + e − i α 2 .
Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Extended Capabilities
Tall Arrays
Calculate with arrays that have more rows than fit in memory.
This function fully supports tall arrays. For more information, see Tall Arrays.
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool .
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox) .
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
This function fully supports distributed arrays. For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox) .
Видео:Скалярное произведение векторов. 9 класс.Скачать

Угол между двумя векторами matlab
Видео:Задача 3. Найти косинус угла между векторами.Скачать

Художественные модели для рисования — эталонные изображения для рисования фигур (NON-NUDE SERIES DLDS # 6) в Ultra HD 4K
Я хочу рассчитать угол между двумя векторами V = [Vx Vy Vz] а также B = [Bx By Bz] . эта формула верна?
и есть ли другой способ его вычислить?
Мой вопрос не в том, чтобы нормализовать векторы или сделать это проще. Я спрашиваю, как получить угол между этими двумя векторами
- 1 Кажется, это скорее вопрос математики, чем вопрос программирования.
- 1 В зависимости от вашего языка вы должны добавить круглые скобки, чтобы убедиться, что продукт оценивается до разделения. Если оценивать слева направо, это было бы неправильно.
Судя по этой ссылке, это кажется наиболее стабильным решением:
- 1 Вот почему я запутался и не знаю, какой из них правильный и почему
- 2 Просто прочитайте больше по предоставленной мной ссылке. Оба они верны в теории, но на практике этот вариант упоминается для обеспечения более стабильных результатов (в то время как альтернатива с acos вычисляет немного быстрее).
Вариантов очень много:
Все формулы из этой ветки mathworks. Говорят, что а3 самая стабильная, но я не знаю почему.
За несколько векторов хранящиеся в столбцах матрицы, можно вычислить углы с помощью этого кода:
Вы можете вычислить VdotB намного быстрее и для векторов произвольной длины с помощью оператора точки, а именно:
Кроме того, как упоминалось в комментариях, в Matlab есть функция точки для прямого вычисления внутренних продуктов.
Кроме того, формула такова, что вы делаете правильно.
- 4 Если вы хотите быть лаконичным, по крайней мере рекомендую V*B’
- 1 Есть ли причина, по которой вы избегаете внутреннего dot функция?
- @HighPerformanceMark Не говоря уже о том, чтобы забыть о его существовании.
- нет, нет причин, и функция точки работает очень хорошо, но я просто написал такой вопрос.
Эта функция должна возвращать угол в радианах.
Решение Денниса Джахеруддина отлично подходит для трехмерных векторов, для векторов более высокой размерности я бы предложил использовать:
Это исправляет числовые проблемы, из-за которых аргумент acos может быть чуть выше 1 или ниже -1. Однако все еще проблематично, когда один из векторов является нулевым вектором. Этот метод также требует всего 3 * N + 1 умножения и 1 sqrt. Однако для этого также требуются 2 сравнения, в которых метод atan не требуется.
📽️ Видео
11 класс, 5 урок, Угол между векторамиСкачать

9 класс, 17 урок, Угол между векторамиСкачать

Математика это не ИсламСкачать

Угол между векторамиСкачать

Задание 3 ЕГЭ профиль #121Скачать
100 тренировочных задач #135 Угол между векторамиСкачать

105. Угол между векторамиСкачать

Геометрия 9 класс (Урок№18 - Угол между векторами. Скалярное произведение векторов.)Скачать

MATLAB 04 Массивы и матрицыСкачать