методическая разработка
Методическая разработка темы «Координаты и векторы» по учебной дисциплине «Математика: алгебра и начала математического анализа; геометрия» для студентов 1 курса специальности 34.02.01 Сестринское дело
- Скачать:
- Предварительный просмотр:
- Прямоугольная система координат в пространстве
- Формулы вычисления расстояния между двумя точками:
- 2. Формулы вычисления расстояния между двумя точками
- Определение вектора
- Коллинеарные вектора
- Сонаправленные вектора
- Компланарные вектора
- Равные вектора
- Единичный вектор
- Формулы длины вектора
- Формула длины вектора для плоских задач
- Формула длины вектора для пространственных задач
- Формулы сложения и вычитания векторов для плоских задач
- Формулы сложения и вычитания векторов для пространственных задач
- Формулы умножения вектора на число
- Формула умножения вектора на число для плоских задач
- Формула умножения вектора на число для пространственных задач
- Выучить определения и формулы
- Ответить на вопросы:
- Коллинеарные вектора
- Сонаправленные вектора
- Лекция на тему: «Векторы».
- «Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
- Примеры задач на равенство векторов
- Примеры плоских задач на равенство векторов
- Примеры пространственных задач на равенство векторов
- Формулы определения координат вектора заданного координатами его начальной и конечной точки
- Формула определения координат вектора для плоских задач
- Формула определения координат вектора для пространственных задач
- Формула определения координат вектора для n -мерного пространства
- Примеры для плоских задач
- Примеры для пространственных задач
- Примеры для n -мерного пространства
- Определение длины вектора
- Формулы длины вектора
- Формула длины вектора для плоских задач
- Формула длины вектора для пространственных задач
- Примеры вычисления длины вектора для плоских задачи
- Примеры вычисления длины вектора для пространственных задачи
- Примеры вычисления длины вектора для пространств с размерностью большей 3
- Формулы скалярного произведения векторов заданных координатами
- Формула скалярного произведения векторов для плоских задач
- Формула скалярного произведения векторов для пространственных задач
- Формула скалярного произведения n -мерных векторов
- Формула вычисления проекции вектора на вектор
- Примеры задач на проекцию вектора
- Примеры вычисления проекции вектора для плоских задач
- Примеры вычисления проекции вектора для пространственных задачи
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Дистанционные курсы для педагогов
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Конспект урока «Векторы в пространстве», 1 курс
- Просмотр содержимого документа «Конспект урока «Векторы в пространстве», 1 курс»
Видео:11 класс, 2 урок, Координаты вектораСкачать

Скачать:
| Вложение | Размер |
|---|---|
| mr_1_sd.docx | 448.33 КБ |
Видео:Координаты вектора. 9 класс.Скачать

Предварительный просмотр:
Областное государственное бюджетное профессиональное образовательное учреждение
«НИЖНЕУДИНСКОЕ МЕДИЦИНСКОЕ УЧИЛИЩЕ»
Рассмотрено ЦМК общеобразовательных, общих гуманитарных, социально-экономических, математических и общих естественнонаучных дисциплин
Председатель ________ / _______________/
«_____» ____________ 2019 г.
темы «Координаты и векторы»
по учебной дисциплине
«Математика: алгебра и начала
математического анализа; геометрия»
для студентов 1 курса
по специальности 34.02.01 Сестринское дело
Организация-разработчик: Областное государственное бюджетное профессиональное образовательное учреждение «Нижнеудинское медицинское училище».
Быкова Н.Г. – преподаватель математики, высшая квалификационная категория
Данная методическая разработка предназначена для проведения учебных занятий по теме «Координаты и векторы» в соответствии с рабочей программой по учебной дисциплине «Математика: алгебра и начала математического анализа; геометрия» для специальности 34.02.01 Сестринское дело.
На изучение данной темы отводится 10 часов по рабочей программе
Прямоугольная система координат в пространстве. 2ч
Расстояния между двумя точками 2ч
Методическая разработка содержит информационный материал в виде опорного конспекта, задания для исходного уровня знаний и контролирующего материала для закрепления знаний, а так же задания для внеаудиторной самостоятельной работы.
Тема: «Прямоугольная система координат в пространстве»
Тип занятия: изучение нового материала
Оснащение: раздаточный материал.
Место проведения: учебный кабинет.
Ввести понятия: Прямоугольная (декартова) система координат в пространстве. Формула расстояния между двумя точками.
- Развитие пространственного воображения учащихся.
- Развивать умения строить логическую цепочку рассуждений, анализировать, выделять главное, сравнивать, строить аналогии, обобщать и систематизировать, делать выводы.
- Развивать умение работать в должном темпе.
- Воспитание умения слушать, умения работать в малых группах.
- Воспитание познавательного интереса к предмету.
- Воспитание умений и навыков самоконтроля при выполнении самостоятельной работы
- Внедрение интерактивных технологий обучения (работа в малых группах).
- Активизация мыслительно-познавательной деятельности учащихся.
- Создание условий для формирования знаний, умений и навыков;
Студент должен уметь:
Применять теорию при решении задач на действия с векторами, координатный метод, применение векторов для вычисления величин углов и расстояний.
Студент должен знать:
Прямоугольная (декартова) система координат в пространстве. Формула расстояния между двумя точками. Понятие вектора. Модуль вектора. Равенство векторов. Сложение векторов. Умножение вектора на число. Разложение вектора по направлениям. Угол между двумя векторами. Проекция вектора на ось. Координаты вектора. Скалярное произведение векторов. Использование координат и векторов при решении математических и прикладных задач.
Технологическая карта занятия
1. Организационный момент
Проверка внешнего вида студентов, отметка отсутствующих
Готовятся к занятию
2.Опеделение целей занятия. Мотивация темы.
Сообщение темы и цели занятия, плана его проведения. Мотивация цели занятия
Слушают, записывают в тетради тему занятия
3.Определение исходного уровня знаний
Отвечает на вопросы с места,
4.Изучение нового материала
Излагает новый материал
Слушают, конспектируют в тетради
5.Закрепление нового материала. Контроль конечного уровня знаний.
Демонстрирует задания, активизирует деятельность студентов, корректирует ответы
6.Рефлексия. Подведение итогов занятия.
Оценивается работа группы и в целом и каждого студента с обоснованием оценок
Анализируют свою работу
7. Домашнее задание
Задает и комментирует домашнее задание
Записывают задание на дом
- Действия над векторами в координатной форме.
- Сложение, вычитание векторов.
- Правило параллелограмма.
- Даны векторы и Постойте векторы:
Видео:9 класс, 2 урок, Координаты вектораСкачать

Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для всех осей. OX — ось абсцисс, OY — ось ординат, OZ — ось апликат. Положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Такая система координат называется правой. Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси ( Рис. 2).
Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: A(a, b, c).
Видео:Координаты точки и координаты вектора 1.Скачать

Формулы вычисления расстояния между двумя точками:
Формула вычисления расстояния между двумя точками A(x a , y a ) и B(x b , y b ) на плоскости:
AB = √(x b — x a ) 2 + (y b — y a ) 2
Формула вычисления расстояния между двумя точками A(x a , y a , z a ) и B(x b , y b , z b ) в пространстве:
AB = √(x b — x a ) 2 + (y b — y a ) 2 + (z b — z a ) 2
Найти расстояние между точками A(-1, 3) и B(6,2).
Найти расстояние между точками A(-1, 3, 3) и B(6, 2, -2)
Найти длину вектора a = .
Найти длину вектора a = .
Найти координаты вектора = , если А (-1; -2), В (4; 5)
Запишите координаты вектора: = 2 +4 -3 , = -3 -2 +2 , = — , = 3 , =- —
Запишите координаты вектора: = 3 +2 -5 , = -2 -3 +4 , = — , = 2 , =- +
Даны векторы , , , запишите разложение этих векторов по координатным векторам , , .
Вершины треугольника имеют координаты А(1; 2; 0), В(5; -1; 3), С(6; 5; 4). Найдите длины сторон треугольника ABC.
Выразить через единичные векторы и следующие векторы:
1) = (-2; 4) 2) = , А (-2; -1), В (4; -3)
1. Выучить формулы
2. Выполнить задание
Вершины треугольника имеют координаты А( -1; 1), В(1; -1), С(0; 4). Найдите длины сторон треугольника ABC.
3. Самостоятельная работа
Подготовить реферат на тему «Векторное задание прямых и плоскостей в пространстве»
Занятие №2. Расстояния между двумя точками
Тип занятия: изучение нового материала
Оснащение: раздаточный материал.
Место проведения: учебный кабинет.
Ввести понятия: Формула расстояния между двумя точками. Использование координат и векторов при решении математических и прикладных задач.
- Развитие пространственного воображения учащихся.
- Развивать умения строить логическую цепочку рассуждений, анализировать, выделять главное, сравнивать, строить аналогии, обобщать и систематизировать, делать выводы.
- Развивать умение работать в должном темпе.
- Воспитание умения слушать, умения работать в малых группах.
- Воспитание познавательного интереса к предмету.
- Воспитание умений и навыков самоконтроля при выполнении самостоятельной работы
- Внедрение интерактивных технологий обучения (работа в малых группах).
- Активизация мыслительно-познавательной деятельности учащихся.
- Создание условий для формирования знаний, умений и навыков;
Студент должен уметь:
Применять теорию при решении задач на применения формулы расстояния между двумя точками, применение векторов для вычисления величин углов и расстояний.
Студент должен знать:
Формула расстояния между двумя точками. Использование координат и векторов при решении математических и прикладных задач.
Технологическая карта занятия
1. Организационный момент
Проверка внешнего вида студентов, отметка отсутствующих
Готовятся к занятию
2.Опеделение целей занятия. Мотивация темы.
Сообщение темы и цели занятия, плана его проведения. Мотивация цели занятия
Слушают, записывают в тетради тему занятия
3.Определение исходного уровня знаний
Приложение № 2. 1
Отвечает на вопросы с места
4.Изучение нового материала
Излагает новый материал
Слушают, конспектируют в тетради
5.Закрепление нового материала. Контроль конечного уровня знаний.
Приложение № 2. 3
Демонстрирует задания, активизирует деятельность студентов, корректирует ответы
6.Рефлексия. Подведение итогов занятия.
Оценивается работа группы и в целом и каждого студента с обоснованием оценок
Анализируют свою работу
7. Домашнее задание
Задает и комментирует домашнее задание
Записывают задание на дом
1. Понятие прямоугольной системы координат в пространстве. Ее элементы.
Видео:Координаты вектора в пространстве. 11 класс.Скачать

2. Формулы вычисления расстояния между двумя точками
1. Выучить определения и формулы
2. Объясните, как задаются точки в пространстве?
∙ Какие прямые называются координатными осями?
∙ Формула расстояния между двумя точками, заданными координатами в пространстве .
Занятие №3 . Векторы.
Тип занятия: изучение нового материала
Оснащение: раздаточный материал.
Место проведения: учебный кабинет.
Ввести понятия: Векторы. Модуль вектора. Равенство векторов. Сложение векторов. Умножение вектора на число. Разложение вектора по направлениям. Угол между двумя векторами. Проекция вектора на ось. Координаты вектора. Скалярное произведение векторов. Использование координат и векторов при решении математических и прикладных задач.
- Развитие пространственного воображения учащихся.
- Развивать умения строить логическую цепочку рассуждений, анализировать, выделять главное, сравнивать, строить аналогии, обобщать и систематизировать, делать выводы.
- Развивать умение работать в должном темпе.
- Воспитание умения слушать, умения работать в малых группах.
- Воспитание познавательного интереса к предмету.
- Воспитание умений и навыков самоконтроля при выполнении самостоятельной работы
- Внедрение интерактивных технологий обучения (работа в малых группах).
- Активизация мыслительно-познавательной деятельности учащихся.
- Создание условий для формирования знаний, умений и навыков;
Студент должен уметь:
Применять теорию при решении задач на действия с векторами, координатный метод, применение векторов для вычисления величин углов и расстояний.
Студент должен знать:
Понятие вектора. Модуль вектора. Равенство векторов. Сложение векторов. Умножение вектора на число. Разложение вектора по направлениям. Угол между двумя векторами. Проекция вектора на ось. Координаты вектора. Скалярное произведение векторов. Использование координат и векторов при решении математических и прикладных задач.
Технологическая карта занятия
1. Организационный момент
Проверка внешнего вида студентов, отметка отсутствующих
Готовятся к занятию
2.Опеделение целей занятия. Мотивация темы.
Сообщение темы и цели занятия, плана его проведения. Мотивация цели занятия
Слушают, записывают в тетради тему занятия
3.Определение исходного уровня знаний
Отвечает на вопросы
4.Изучение нового материала
Излагает новый материал
Слушают, конспектируют в тетради
5.Закрепление нового материала. Контроль конечного уровня знаний.
Приложение № 3 .3
Демонстрирует задания, активизирует деятельность студентов, корректирует ответы
6.Рефлексия. Подведение итогов занятия.
Оценивается работа группы и в целом и каждого студента с обоснованием оценок
Анализируют свою работу
7. Домашнее задание
Приложение № 3. 4
Задает и комментирует домашнее задание
Записывают задание на дом
- вектор в пространстве,
- длина по координатам начала и конца вектора
- основные действия над векторами: сложение, вычитание, умножение на число
- коллинеарные
- компланарные векторы.
В наши дни понятие «вектор» постоянно встречается в газетных и журнальных публикациях, в выступлениях политиков, ученых, педагогов. Обсуждая важнейшие процессы в жизни общества, говорят о векторе реформ и его социальной составляющей, о векторе экономических преобразований и его изменении, о направлении вектора развития системы образования. Понятие о векторе как направленном отрезке вошло в сознание и речь современного образованного человека. Термин «вектор» ввел в науку в середине XIX в. выдающийся ученый Уильям Гамильтон (1805-1865), профессор астрономии в Дублинском университете и королевский астроном Ирландии. Механика и астрономия дали важнейший импульс процессу создания векторного исчисления, где впервые были изучены векторные величины — сила и скорость. Еще в школе Аристотеля был введен термин «сложение движений», т. е. скоростей и астрономы средневекового Востока постоянно использовали «сложение движений». В 1844 г. в первой публикации по теории кватернионов Гамильтон ввел термин «вектор», образовав его от латинского слова «vehere» — «нести». Он писал: «Шаг от точки А к точке В можно рассматривать как работу по транспортировке или переносу подвижной точки из начального положения в конечное».
Так в геометрии трудами многих ученых к середине XIX в. была создана теория направленных отрезков, включающая операции сложения и вычитания, умножения на число, отыскания длин отрезков и углов между ними.
В курсе 9 класса вы изучали векторы на плоскости.
Перед нами стоит задача – дать определение вектора в пространстве, научиться находить его длину по координатам начала и конца вектора и рассмотреть основные действия над векторами: сложение, вычитание, умножение на число, а также рассмотреть коллинеарные и компланарные векторы.
Поставленную перед нами задачу мы будем решать на основе сравнительного анализа и установления закономерностей: как давались определения вектора и операций над векторами на плоскости и как они формулируются для векторов в пространстве. На каждой парте лежат опорные конспекты, правую часть которых необходимо заполнить учащимся, пользуясь материалом учебника.
Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Определение вектора
Вектор — это направленный отрезок, то есть отрезок, имеющий длину и определенное направление. Графически вектора изображаются в виде направленных отрезков прямой определенной длины. (рис.1)
Вектор началом которого есть точка А, а концом — точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a.
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.
Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.
Определение. Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают. Нулевой вектор обычно обозначается как 0.Длина нулевого вектора равна нулю.
Видео:90. Координаты вектораСкачать
Коллинеарные вектора
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 2).
Видео:Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Сонаправленные вектора
Определение. Два коллинеарных вектора a и b называются сонаправленными векторами, если их направления совпадают: a↑↑b (рис. 3).
Противоположно направленные вектора
Определение. Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a↑↓b (рис. 4).
Видео:Координаты вектора.Скачать

Компланарные вектора
Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами . (рис. 5).
Всегда возможно найти плоскости параллельную двум произвольным векторам, по-этому любые два вектора всегда компланарные.
Видео:Математика это не ИсламСкачать

Равные вектора
Определение. Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны (рис. 6).
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины: a = b, если a↑↑b и |a| = |b|.
Видео:18+ Математика без Ху!ни. Векторное произведение.Скачать

Единичный вектор
Единичным вектором или ортом — называется вектор, длина которого равна единице.
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.
Длина вектора |a| в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.
Видео:Встреча с Путиным в общежитии МГУ на Воробьевых горах!Скачать

Формулы длины вектора
Формула длины вектора для плоских задач
В случае плоской задачи модуль вектора a = можно найти воспользовавшись следующей формулой:
|a| = √a x 2 + a y 2
Формула длины вектора для пространственных задач
В случае пространственной задачи модуль вектора a = можно найти воспользовавшись следующей формулой:
|a| = √a x 2 + a y 2 + a z 2
Формулы сложения и вычитания векторов для плоских задач
В случае плоской задачи сумму и разность векторов a = и b = можно найти воспользовавшись следующими формулами:
Формулы сложения и вычитания векторов для пространственных задач
В случае пространственной задачи сумму и разность векторов a = и b = можно найти воспользовавшись следующими формулами:
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Формулы умножения вектора на число
Формула умножения вектора на число для плоских задач
В случае плоской задачи произведение вектора a = и числа k можно найти воспользовавшись следующей формулой:
Формула умножения вектора на число для пространственных задач
В случае пространственной задачи произведение вектора a = и числа k можно найти воспользовавшись следующей формулой:
При каких значениях k и c данные векторы коллинеарные:
Выяснить при каких значениях m и n данные векторы коллинеарные: и .
Дан вектор ( -1; -2). Найдите координаты точки В, если известны координаты точки А:
Перпендикулярны ли векторы:
1) (-2;3) и (-1;2); 2) (4;-1) и (3;12); 3) (3,5; 2; -1) и (4; -1,25; 0,5); 4) (2; 3; -5) и (-1; 4; 2).
Коллинеарны ли векторы:
1) (1;2) и (-2;-4); 2) (1;-1;2) и (2; 2;-4);
3) и , если А (8;2), В (3;4), С (11;7), D (21, 19).
Найти сумму векторов a = и b = .
Найти сумму векторов a = и b = .
Найти разность векторов a = и b = .
Найти разность векторов a = и b = .
Найти произведение вектора a = на 3.
Найти произведение вектора a = на -2.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Выучить определения и формулы
Видео:9 класс, 3 урок, Связь между координатами вектора и координатами его начала и концаСкачать

Ответить на вопросы:
Видео:Координаты вектора | Геометрия 7-9 класс #86 | ИнфоурокСкачать

Коллинеарные вектора
Видео:ГЕОМЕТРИЯ 9 класс: Координаты векторовСкачать

Сонаправленные вектора
2. Выполнить задание
Найти сумму векторов a = и b = .
Использование координат и векторов при решении математических и прикладных задач.
Тип занятия: обобщение и систематизация знаний
Вид занятия: практическое занятие
Оснащение: раздаточный материал.
Место проведения: учебный кабинет.
Обобщение понятий: Прямоугольная (декартова) система координат в пространстве. Формула расстояния между двумя точками. Векторы. Модуль вектора. Равенство векторов. Сложение векторов. Умножение вектора на число. Разложение вектора по направлениям. Угол между двумя векторами. Проекция вектора на ось. Координаты вектора. Скалярное произведение векторов. Использование координат и векторов при решении математических и прикладных задач.
- Развитие пространственного воображения учащихся.
- Развивать умения строить логическую цепочку рассуждений, анализировать, выделять главное, сравнивать, строить аналогии, обобщать и систематизировать, делать выводы.
- Развивать умение работать в должном темпе.
- Воспитание умения слушать, умения работать в малых группах.
- Воспитание познавательного интереса к предмету.
- Воспитание умений и навыков самоконтроля при выполнении самостоятельной работы
- Внедрение интерактивных технологий обучения (работа в малых группах).
- Активизация мыслительно-познавательной деятельности учащихся.
- Создание условий для формирования знаний, умений и навыков;
Студент должен уметь:
Применять теорию при решении задач на действия с векторами, координатный метод, применение векторов для вычисления величин углов и расстояний.
Студент должен знать:
Прямоугольная (декартова) система координат в пространстве. Формула расстояния между двумя точками. Понятие вектора. Модуль вектора. Равенство векторов. Сложение векторов. Умножение вектора на число. Разложение вектора по направлениям. Угол между двумя векторами. Проекция вектора на ось. Координаты вектора. Скалярное произведение векторов. Использование координат и векторов при решении математических и прикладных задач.
Тип занятия: закрепления изученного материала
Видео:Координаты вектора. Видеоурок по геометрии 9 классСкачать

Лекция на тему: «Векторы».
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:§3 Координаты вектораСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
Вектор — это отрезок, который имеет направление. Конец вектора совпадает со стрелкой, начало — точка. Модуль вектора (абсолютная величина) — длина этого направленного отрезка.
Если начало вектора совпадает с его концом, получим нулевой вектор.
Два вектора являются равными , если их длина одинаковая и они имеют одинаковое направление. Они совмещаются при переносе.
Определение. Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.
Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.
Определение. Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.
Нулевой вектор обычно обозначается как 0.
Длина нулевого вектора равна нулю.
Определение. Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 2).
Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны , если существует число n такое, что
Условия коллинеарности векторов 2. Два вектора коллинеарны , если отношения их координат равны.
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
Условия коллинеарности векторов 3. Два вектора коллинеарны , если их векторное произведение равно нулевому вектору.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
Определение. Два коллинеарных вектора a и b называются сонаправленными векторами , если их направления совпадают: a↑↑b (рис. 3).
Противоположно направленные вектора
Определение. Два коллинеарных вектора a и b называются противоположно направленными векторами , если их направления противоположны: a↑↓b (рис. 4).
Определение. Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами . (рис. 5).
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.
Условия компланарности векторов
Для 3-х векторов. Три вектора компланарны если их смешанное произведение равно нулю.
Для 3-х векторов. Три вектора компланарны если они линейно зависимы.
Для n векторов. Вектора компланарны если среди них не более двух линейно независимых векторов.
Определение. Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны (рис. 6).
Условие равенства векторов. Вектора равны , если их координаты равны.
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b , если a ↑↑ b и | a | = | b |.
Примеры задач на равенство векторов
Примеры плоских задач на равенство векторов
Пример 1. Определить какие из векторов равны a = , b = , c = .
a = b — так как их координаты равны,
a ≠ c — так как их координаты не равны,
b ≠ c — так как их координаты не равны.
Пример 2. При каком значении параметра n вектора a = и b = равны.
Проверим равенство компонентов векторов
a x = b x = 1
a y = b y => 8 = 2 n => n = 8/2 = 4
Ответ: при n = 4 вектора a и b равны.
Примеры пространственных задач на равенство векторов
Пример 3. Определить какие из векторов равны a = , b = , c = .
a = c — так как их координаты равны,
a ≠ b — так как их координаты не равны,
b ≠ c — так как их координаты не равны.
Пример 4. При каком значении параметра n вектора a = и b = равны.
Проверим равенство компонентов векторов
a x = b x = 1
a y = b y = 2
a z = b z => 4 = 2 n => n = 4/2 = 2
Ответ: при n = 2 вектора a и b равны.
Определение. Единичным вектором или ортом — называется вектор, длина которого равна единице.
Основное соотношение. Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.
Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1).
Условие ортогональности векторов. Два вектора a и b ортогональны (перпендикулярны) , если их скалярное произведение равно нулю.
Формулы определения координат вектора заданного координатами его начальной и конечной точки
Формула определения координат вектора для плоских задач
В случае плоской задачи вектор AB заданный координатами точек A(A x ; A y ) и B(B x ; B y ) можно найти воспользовавшись следующей формулой
Формула определения координат вектора для пространственных задач
В случае пространственной задачи вектор AB заданный координатами точек A(A x ; A y ; A z ) и B(B x ; B y ; B z ) можно найти воспользовавшись следующей формулой
Формула определения координат вектора для n -мерного пространства
В случае n -мерного пространства вектор AB заданный координатами точек A(A 1 ; A 2 ; . ; A n ) и B(B 1 ; B 2 ; . ; B n ) можно найти воспользовавшись следующей формулой
Примеры для плоских задач
Пример 1. Найти координаты вектора AB, если A(1; 4), B(3; 1).
Пример 2. Найти координаты точки B вектора AB = , если координаты точки A(3; -4).
Пример 3. Найти координаты точки A вектора AB = , если координаты точки B(3; -4).
Примеры для пространственных задач
Пример 4. Найти координаты вектора AB, если A(1; 4; 5), B(3; 1; 1).
Пример 5. Найти координаты точки B вектора AB = , если координаты точки A(3; -4; 3).
Пример 6. Найти координаты точки A вектора AB = , если координаты точки B(3; -4; 1).
Примеры для n -мерного пространства
Пример 7. Найти координаты вектора AB, если A(1; 4; 5; 5; -3), B(3; 0; 1; -2; 5).
Пример 8. Найти координаты точки B вектора AB = , если координаты точки A(3; -4; 3; 2).
Пример 9. Найти координаты точки A вектора AB = , если координаты точки B(3; -4; 1; 8).
Определение длины вектора
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.
Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.
Основное соотношение. Длина вектора | a | в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.
Формулы длины вектора
Формула длины вектора для плоских задач
В случае плоской задачи модуль вектора a = < a x ; a y > можно найти воспользовавшись следующей формулой:
Формула длины вектора для пространственных задач
В случае пространственной задачи модуль вектора a = < a x ; a y ; a z > можно найти воспользовавшись следующей формулой:
Примеры вычисления длины вектора для плоских задачи
Пример 1. Найти длину вектора a = .
Решение: | a | = √ 2 2 + 4 2 = √ 4 + 16 = √ 20 = 2√ 5 .
Пример 2. Найти длину вектора a = .
Решение: | a | = √ 3 2 + (-4) 2 = √ 9 + 16 = √ 25 = 5.
Примеры вычисления длины вектора для пространственных задачи
Пример 3. Найти длину вектора a = .
Решение: | a | = √ 2 2 + 4 2 + 4 2 = √ 4 + 16 + 16 = √ 36 = 6.
Пример 4. Найти длину вектора a = .
Решение: | a | = √ (-1) 2 + 0 2 + (-3) 2 = √ 1 + 0 + 9 = √ 10 .
Примеры вычисления длины вектора для пространств с размерностью большей 3
Пример 5. Найти длину вектора a = .
Решение: | a | = √ 1 2 + (-3) 2 + 3 2 + (-1) 2 = √ 1 + 9 + 9 + 1 = √ 20 = 2√ 5
Пример 6. Найти длину вектора a = .
Решение: | a | = √ 2 2 + 4 2 + 4 2 + 6 2 + 2 2 = √ 4 + 16 + 16 + 36 + 4 = √ 76 = 2√ 19 .
Формулы скалярного произведения векторов заданных координатами
Формула скалярного произведения векторов для плоских задач
В случае плоской задачи скалярное произведение векторов a = < a x ; a y > и b = < b x ; b y > можно найти воспользовавшись следующей формулой:
Формула скалярного произведения векторов для пространственных задач
В случае пространственной задачи скалярное произведение векторов a = < a x ; a y ; a z > и b = < b x ; b y ; b z > можно найти воспользовавшись следующей формулой:
Формула скалярного произведения n -мерных векторов
В случае n -мерного пространства скалярное произведение векторов a = < a 1 ; a 2 ; . ; a n > и b = < b 1 ; b 2 ; . ; b n > можно найти воспользовавшись следующей формулой:
Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:
a · b = |a| · |b| cos α
Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.
Определение. Проекцией вектора AB на ось l называется число, равное величине отрезка A 1 B 1 оси l , где точки A 1 и B 1 являются проекциями точек A и B на ось l . (рис. 1).
Определение. Проекцией вектора a на направление вектора b , называется число, равное величине проэкции вектора a на ось проходящую через вектор b .
Формула вычисления проекции вектора на вектор
Для вычисления проекции вектора a на направление вектора b из определения скалярного произведения получена формула:
Примеры задач на проекцию вектора
Примеры вычисления проекции вектора для плоских задач
Пример 1. Найти проекцию вектора a = на вектор b = .
Найдем скалярное произведение этих векторов
a · b = 1 · 3 + 2 · 4 = 3 + 8 = 11
Найдем модуль вектора b
| b | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
Найдем проекцию вектора a на вектор b
Примеры вычисления проекции вектора для пространственных задачи
Пример 2. Найти проекцию вектора a = на вектор b = .
Найдем скалярное произведение этих векторов
a · b = 1 · 4 + 4 · 2 + 0 · 4 = 4 + 8 + 0 = 12
Найдем модуль вектора b
| b | = √ 4 2 + 2 2 + 4 2 = √ 16 + 4 + 16 = √ 36 = 6
Найдем проекцию вектора a на вектор b
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 949 человек из 80 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 325 человек из 69 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 698 человек из 75 регионов
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 482 651 материал в базе
Материал подходит для УМК
«Геометрия. Базовый уровень», Шарыгин И.Ф.
9*. Движения пространства
Дистанционные курсы для педагогов
Другие материалы
- 13.06.2019
- 5047
- 13.06.2019
- 283
- 13.06.2019
- 505
- 06.06.2019
- 233
- 22.05.2019
- 765
- 11.04.2019
- 4828
- 14.01.2019
- 1769
- 12.01.2019
- 415
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 13.06.2019 3787 —> —> —> —>
- DOCX 3.1 мбайт —> —>
- Оцените материал:
Настоящий материал опубликован пользователем Аюпова Илюза Каюмовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 3 года и 1 месяц
- Подписчики: 0
- Всего просмотров: 25958
- Всего материалов: 21
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
548 курсов от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей
Время чтения: 1 минута
Первые результаты по сокращению отчетности у учителей ожидаются осенью
Время чтения: 1 минута
Крупнейшие вузы Татарстана откроют цифровые кафедры в 2022 году
Время чтения: 1 минута
В России утвердили новые правила аккредитации образовательных учреждений
Время чтения: 1 минута
В Якутске все классы, кроме девятых и одиннадцатых, перейдут на удаленку
Время чтения: 1 минута
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Конспект урока «Векторы в пространстве», 1 курс
Конспект урока «Векторы в пространстве», 1 курс
Просмотр содержимого документа
«Конспект урока «Векторы в пространстве», 1 курс»
ОГБПОУ Фурмановский технический колледж, преподаватель Цветкова Елена Ивановна
Разработка урока на тему:
Векторы в пространстве. Действия с векторами. Разложение вектора на составляющие.
Ввести определения вектора в пространстве, равенства векторов. Рассмотреть правила действия над векторов, правило сложения нескольких векторов в пространстве.
Воспитывать личностные качества обучающихся (умение слушать), доброжелательность по отношению к окружающим, внимательность, аккуратность, дисциплинированность.
Развивать пространственное воображение и логическое мышление обучающихся, умение быстро ориентироваться в обстановке; развивать сообразительность, находчивость, тренировать память.
1. Орг. момент. Настрой на урок.
2. Мотивация урока.
Поразмышляйте над содержанием пословицы «Плохо, когда сила живет без ума, да нехорошо, когда и ум без силы». То есть, если есть сила, то надо знать, куда ее направить. От этого зависит, будет ли пружина сжиматься или растягиваться, полетит ли мяч в ворота противника или в собственные и многое другое. Вы уже, конечно, догадались, что сегодня речь пойдет о векторах, причем о векторах в пространстве. Геометрия – одна из самых интереснейших наук, которая изучает много важных и интересных тем. Одна из них – это “Векторы”. С понятием “Вектор” вы уже знакомы, но вы знакомы с векторами на плоскости, а сегодня мы пополним свои знания о векторах и рассмотрим “Векторы в пространстве”
3. Актуализация опорных знаний. Проверка д/з.
Решить № 8, стр. 68.
Что называется вектором на плоскости?
Приведите пример векторных величин.
Что такое абсолютная величина вектора; направление вектора?
Какие векторы называются равными?
Сформулируйте правила сложения двух векторов на плоскости.
Какой вектор называют разницей двух векторов?
4. Объяснение нового материала сопровождается презентацией:
Впервые понятие вектора появилось в работах немецкого математика 19 века Г. Грассмана и ирландского математика У. Гамильтона; затем его использовали в своих открытиях многие ученые. Современная символика для обозначения вектора была введена в 1853 году французским математиком О. Коши. Применение векторов играет важнейшую роль в современной математике, химии, биологии, экономике и в других науках.
Векторы на плоскости были изучены в 9 классе в разделе “Планиметрия”. Сегодня на уроке рассмотрим векторы в пространстве. Определение вектора в пространстве и связанные с ним понятия сходны с определением вектора на плоскости и связанными с ним понятиями.
Раз мы уже знакомы с векторами на плоскости, то нам будет не трудно говорить о векторах в пространстве. Результатом нашей работы станет опорный конспект.
Что такое вектор? Как построить вектор? Как обозначаются вектора?
Обратите внимание: что над буквенным обозначением вектора ставится стрелка или черта- в разной литературе по- разному. Так, например, в учебнике физики — стрелка, а в учебнике геометрии — черта.
Вектором называется направленный отрезок.
Вектор характеризуется следующими элементами:
1) начальной точкой (точкой приложения);
2 )направлением;
3) длиной («модулем вектора»).
Если начало вектора — точка А, а его конец — точка В, то вектор обозначается 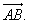
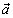

От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос.
Нулевой вектор — точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления. Обозначается: 
Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора 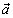

Два вектора называются равными, если они совмещаются параллельным переносом.
АВСD — параллелограмм,
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Если векторы 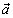
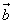
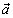
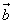
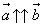
Если векторы 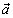

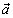

Обозначаются 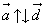
Свойство коллинеарных векторов
Если векторы 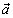
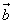
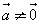
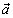
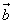
Правило треугольника. Каковы бы ни были точки А, В, С, имеет место векторное равенство:
Правило параллелограмма. Если векторы 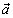
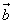
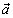
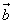
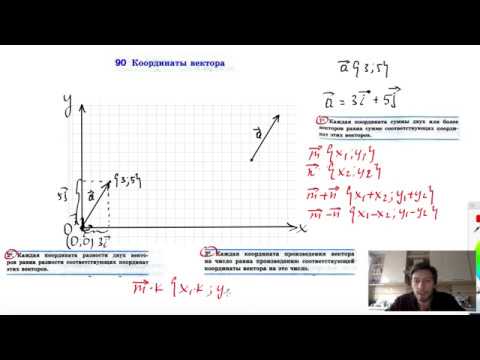
Координаты вектора. Числа x, y и z называются координатами вектора в данном базисе. В этом случае пишут:
Действия над векторами, заданными своими координатами
При сложении векторов их соответстветственные координаты
складываются.
При вычитании векторов их соответстветственные координаты
вычитаются.
При умножении вектора на число все его координаты умножаются на это число.
5. Первичное закрепление нового материала. Выполнение устных упражнений
Дан прямоугольный параллелепипед. Назовите сонаправленные векторы; противоположно направленные векторы.
Запишите координаты вектора АО, если А(6;-2;4), О – начало координат?
Найти координаты вектора АВ, если А(3; 4; -1) и В( -2; 0; 4)
Дано: АВ= СD, где А ( 1;0;1),В ( -1; 1;2), С (0;2;-1). Найти: D( х ,у,z)
Коллективное решение задач:
В пространстве даны точки А, В, С, D. Найдите вектор с началом и концом в этих точках, который равен: а) ВС+СА+АD; б) АВ+ВD+BA-CD.
Найдите координаты конца вектора АВ(1;-3;7), если А(2;5;-1).
У какого из приведенных векторов самая большая длина:
Решить № 3, 5, 6, 7 стр.73
6. Зарядка для глаз.
Решение задач П-23,24. Устно 1-3,5,10,11. П-23, 1-3,
Работа в группах остальные номера.
Итоги урока. Рефлексия.
Что называют вектором?
Выполняется ли правило параллелограмма и правило треугольника в случае сложения векторов в пространстве?
Сформулируйте правило параллелепипеда для сложения векторов в пространстве?
Какие векторы называются равными?
Какие векторы называются сонаправленными в пространстве; противоположно направленными в пространстве?
Д/з: учить пп. 23, 24. Решить : 14,15. Сообщение «Применение векторов».