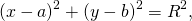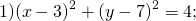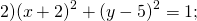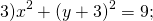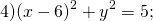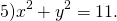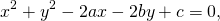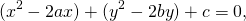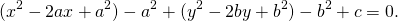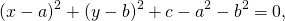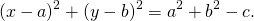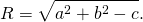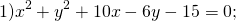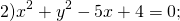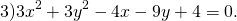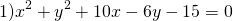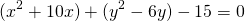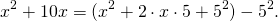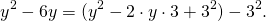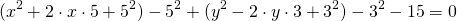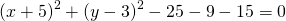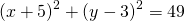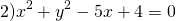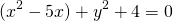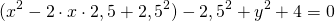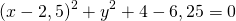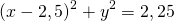Координаты центра окружности примеры (5 видео)

Найти центр и радиус окружности

Если окружность задана уравнением вида

найти центр (a;b) и радиус R такой окружности несложно.

Определить по уравнению окружности координаты её центра и радиуса:

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

Центр окружности — (0;-3), радиус R=3.

Центр — в точке (6;0), радиус R=√5.

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c

Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:

Центром этой окружности является точка (-5;3), радиус R=7.

Центр окружности — точка (2,5;0), радиус R=1,5.

Содержание

Как найти координаты центр окружности??
Декартовы координаты точек плоскости. Уравнение окружности
Числовая ось
Прямоугольная декартова система координат на плоскости
Формула для расстояния между двумя точками координатной плоскости
Уравнение окружности на координатной плоскости
💡 Видео

Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Как найти координаты центр окружности??

Инструкция
1
Аналитически окружность задается уравнением вида (x-x0)²+(y-y0)²=R², где x0 и y0 − координаты центра окружности, R − ее радиус. Итак, центр окружности (x0;y0) здесь задан в явном виде.
2
Пример. Установите центр фигуры, заданной в декартовой системе координат уравнением (x-2)²+(y-5)²=25.
Решение. Данное уравнение является уравнением окружности. Ее центр имеет координаты (2;5). Радиус такой окружности равен 5.
3
Уравнение x²+y²=R² соответствует окружности с центром в начале координат, то есть, в точке (0;0). Уравнение (x-x0)²+y²=R² означает, что центр окружности имеет координаты (x0;0) и лежит на оси абсцисс. Вид уравнения x²+(y-y0)²=R² говорит о расположении центра с координатами (0;y0) на оси ординат.
4
Общее уравнение окружности в аналитической геометрии запишется как: x²+y²+Ax+By+C=0. Чтобы привести такое уравнение к выше обозначенному виду, надо сгруппировать члены и выделить полные квадраты: [x²+2(A/2)x+(A/2)²]+[y²+2(B/2)y+(B/2)²]+C-(A/2)²-(B/2)²=0. Для выделения полных квадратов, как можно заметить, требуется добавлять дополнительные величины: (A/2)² и (B/2)². Чтобы знак равенства сохранялся, эти же величины надо вычесть. Прибавление и вычитание одного и того же числа не меняет уравнения.
5
Таким образом, получается: [x+(A/2)]²+[y+(B/2)]²=(A/2)²+(B/2)²-C. Из этого уравнения уже видно, что x0=-A/2, y0=-B/2, R=√[(A/2)²+(B/2)²-C]. Кстати, выражение для радиуса можно упростить. Домножьте обе части равенства R=√[(A/2)²+(B/2)²-C] на 2. Тогда: 2R=√[A²+B²-4C]. Отсюда R=1/2·√[A²+B²-4C].
6
Окружность не может быть графиком функции в декартовой системе координат, так как, по определению, в функции каждому x соответствует единственное значение y, а для окружности таких «игреков» будет два. Чтобы убедиться в этом, проведите перпендикуляр к оси Ox, пересекающий окружность. Вы увидите, что точек пересечения две.
7
Но окружность можно представить как объединение двух функций: y=y0±√[R²-(x-x0)²]. Здесь x0 и y0, соответственно, представляют собой искомые координаты центра окружности. При совпадении центра окружности с началом координат объединение функций принимает вид: y=√[R²-x²].

Видео:Уравнение окружности (1)Скачать

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Видео:Найти центр и радиус окружностиСкачать

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Видео:УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.