Геометрия 9 класс Контрольные работы по геометрии в четырех вариантах. Используется в комплекте с учебником «Геометрия» (авт. А.Г. Мерзляк, В.Б. Полонский, М.С. Якир). Цитаты из пособия «Геометрия 9 класс. Методическое пособие / Е.В. Буцко и др. — М.: Вентана-Граф» использованы в учебных целях.
- Геометрия 9 класс (Мерзляк) Контрольные работы:
- Геометрия 9 класс Контрольные (Мерзляк): 2 комментария
- Добавить комментарий Отменить ответ
- Предметы
- Новые работы
- Найти контрольную:
- Авторы работ и УМК
- Предметы
- Важные страницы
- Популярное
- Предупреждение
- Контрольные работы по геометрии в 9 классе (УМК А.Г. Мерзляк) материал по геометрии (9 класс)
- Скачать:
- Предварительный просмотр:
- Контрольная работа № 4 по теме «Векторы» (9 класс, Мерзляк А.Г. и др.)
- Просмотр содержимого документа «Контрольная работа № 4 по теме «Векторы» (9 класс, Мерзляк А.Г. и др.)»
- 📹 Видео
Геометрия 9 класс (Мерзляк)
Контрольные работы:
К-1 «Решение треугольников»
К-2 «Правильные многоугольники»
К-3 «Декартовы координаты»
К-4 «Векторы»
К-5 «Геометрические преобразования»
К-6 «Обобщение и систематизация знаний учащихся» (Итоговая за 9 класс)
6 контрольных работ в соответствии с календарным планированием. Каждая работа содержит 4 варианта. Такой обширный материал поможет учителю организовать объективный и эффективный контроль знаний.
Адресовано учителям, работающим по учебнику «Геометрия. 9 класс» авторов А.Г. Мерзляка, В.Б. Полонского, М.С. Якира.
Вы смотрели: Геометрия 9 класс Контрольные работы по геометрии в четырех вариантах УМК Мерзляк, Полонский, Якир.
Видео:ВЕКТОРЫ. Контрольная № 4 Геометрия 9 класс.Скачать

Геометрия 9 класс Контрольные (Мерзляк): 2 комментария
Когда будут опубликованы остальные контрольные по геометрии за 9 класс? У нас например итоговая за 9 класс контрольная завтра, а ее здесь еще нет
Итоговая работа опубликована.
Добавить комментарий Отменить ответ
Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Предметы
Видео:РАЗБОР КОНТРОЛЬНОЙ РАБОТЫ | 9 КЛАСС ГЕОМЕТРИЯ АТАНАСЯН | ВЕКТОРЫСкачать

Новые работы
Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Найти контрольную:
Видео:9 кл Геометрия КР№1 ВекторыСкачать

Авторы работ и УМК
Видео:ДЕКАРТОВЫ КООРДИНАТЫ. Контрольная № 3 Геометрия 9 класс.Скачать

Предметы
Видео:Геометрия 9 Контрольная 4 (Мерзляк). Контрольная работа по геометрии в 9 классе «Векторы»Скачать

Важные страницы
Соглашение о конфиденциальности
(с) 2021. Дистанционный информационный Центр НПИ (г.Москва). Бесплатная помощь школьникам, находящимся на домашнем или семейном обучении. Цитаты из учебных пособий размещены в учебных целях. Контакты: kip1979@mail.ru
Видео:Геометрия 9. Подготовка к КР по теме ВекторыСкачать

Популярное
Видео:Координаты вектора. 9 класс.Скачать

Предупреждение
Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie, пользовательских данных (сведения о местоположении; тип и версия ОС; тип и версия Браузера; тип устройства и разрешение его экрана; источник откуда пришел на сайт пользователь; с какого сайта или по какой рекламе; язык ОС и Браузера; какие страницы открывает и на какие кнопки нажимает пользователь; ip-адрес) в целях функционирования сайта, проведения ретаргетинга и проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.
Видео:Контрольная работа №2. Геометрия. 9 класс. 2 вариант.Скачать

Контрольные работы по геометрии в 9 классе (УМК А.Г. Мерзляк)
материал по геометрии (9 класс)
Представлены контрольные работы по геометрии в 9 классе (УМК А.Г.Мерзляк, базовый уровень). Всего 6 контрольных работ, каждая из которых содержит 4 однотипных варианта. Предусмотрена уровневая дифференциация, которая позволяет провести проверку знаний в любом классе.
Видео:9 класс КОНТРОЛЬНАЯ РАБОТА №1 по ГЕОМЕТРИИ - МерзлякСкачать

Скачать:
| Вложение | Размер |
|---|---|
| geometriya-9_k.r._bazovyy_uroven.docx | 34.65 КБ |
Видео:9 класс КОНТРОЛЬНАЯ РАБОТА №4 по ГЕОМЕТРИИ - МерзлякСкачать

Предварительный просмотр:
Контрольная работа № 1
по теме: «Решение треугольников»
1. Две стороны треугольника равны 6 см и 8 см, а угол между ними 60 
2. В треугольнике АВС известно, что АВ= 3 



3. Определите, остроугольным, прямоугольным или тупоугольным является треугольник со сторонами 7 см, 10 см и 13 см.
4. Одна сторона треугольника на 8 см больше другой, а угол между ними равен 120 
5. Найдите радиус окружности, описанной около треугольника со сторонами 13 см, 20 см и 21 см.
6. Две стороны треугольника равна 6 см и 8 см, а медиана, проведённая к третьей стороне — 
Контрольная работа № 1
по теме: «Решение треугольников»
1. Две стороны треугольника равны 10 см и 12 см, а угол между ними 120 
2.В треугольнике АВС известно, что АС= 5 



3. Определите, остроугольным, прямоугольным или тупоугольным является треугольник со сторонами 6 см, 8 см и 11 см.
4. Одна сторона треугольника на 3 см меньше другой, а угол между ними равен 60 
5. Найдите радиус окружности, вписанной в треугольник со сторонами 4 см, 13 см и 15 см.
6. Стороны треугольника равны 4 см, 5 см и 7 см. Найдите медиану треугольника, проведённую к его меньшей стороне.
Контрольная работа № 1
по теме: «Решение треугольников»
1. Две стороны треугольника равны 8 см и 4 

2. В треугольнике АВС известно, что 



3. Определите, остроугольным, прямоугольным или тупоугольным является треугольник со сторонами 5 см, 9см и 12 см.
4. Одна сторона треугольника на 6 см больше другой, а угол между ними равен 120 
5. Найдите радиус окружности, описанной около треугольника со сторонами 18 см, 20 см и 34 см.
6. Две стороны треугольника равна 7 см и 9 см, а медиана, проведённая к третьей стороне 
Найдите неизвестную сторону треугольника.
Контрольная работа № 1
по теме: «Решение треугольников»
1. Две стороны треугольника равны 6 см и 4 

2. В треугольнике АВС известно, что АС= 9 



3. Определите, остроугольным, прямоугольным или тупоугольным является треугольник со сторонами 9 см, 10 см и 14 см.
4. Одна сторона треугольника на 10 см меньше другой, а угол между ними равен 60 
5. Найдите радиус окружности, вписанной в треугольник со сторонами 5 см, 12 см и 15 см.
6. Стороны треугольника равны 5 см, 7 см и 10 см. Найдите медиану треугольника, проведённую к его большей стороне.
Контрольная работа № 2
по теме: «Правильные многоугольники»
1. Найдите углы правильного сорокаугольника.
2. Найдите длину окружности, вписанной в правильный треугольник со стороной 12 см.
3. В окружность вписан квадрат со стороной 8 см. Найдите сторону правильного шестиугольника, описанного около этой окружности.
4. Радиус окружности, описанной около правильного многоугольника, равен 4 см, а сторона многоугольника – 4 
5. Сторона треугольника равна 6 

6. Углы правильного треугольника со сторонами 6 см срезали так, что получили правильный шестиугольник. Найдите сторону образовавшегося шестиугольника.
Контрольная работа № 2
по теме: «Правильные многоугольники »
1. Найдите углы правильного сорокапятиугольника.
2. Найдите площадь круга, вписанного в правильный шестиугольник со стороной 10 см.
3. Около окружности описан правильный треугольник со стороной 18 см. Найдите сторону квадрата , вписанного в эту окружность.
4. Радиус окружности, вписанной в правильный многоугольник, равен 5 см, а сторона многоугольника — 10 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.
5. Сторона треугольника равна 8 

6. Углы квадрата со стороной 8 см срезали так, что получили правильный восьмиугольник. Найдите сторону образовавшегося восьмиугольника.
Контрольная работа № 2
по теме: «Правильные многоугольники»
1. Найдите углы правильного тридцатишестиугольника.
2. Найдите длину окружности, вписанной в правильный треугольник со стороной 9 см.
3. В окружность вписан правильный шестиугольник со стороной 9 см. Найдите сторону правильного треугольника, описанного около этой окружности.
4. Радиус окружности, описанной около правильного многоугольника, равен 8 
5. Сторона треугольника равна 5 см, а прилежащие к ней углы равны 
6. Углы правильного треугольника срезали так, что получили правильный шестиугольник со стороной 8 см. Найдите сторону данного треугольника.
Контрольная работа № 2
по теме: «Правильные многоугольники»
1. Найдите углы правильного тридцатиугольника.
2. Найдите площадь круга, описанного около квадрата со стороной 16 см.
3. Около окружности описан квадрат со стороной 36 см. Найдите сторону правильного треугольника , вписанного в эту окружность.
4. Радиус окружности, вписанной в правильный многоугольник, равен 12 см, а сторона многоугольника 8 
5. Сторона треугольника равна 10 

6. Углы квадрата срезали так, что получили правильный восьмиугольник со стороной 4 см. Найдите сторону данного квадрата.
Контрольная работа № 3
по теме: « Декартовы координаты»
1. Найдите длину отрезка ВС и координаты его середины, если В (-2;5) и С (4;1).
2. Составьте уравнение окружности, центр которой находится в точке А (-1;2) и которая проходит через точку М (1;7).
3. Найдите координаты вершины В параллелограмма АВСD, если А (3;-2), С (9;8), D (-4;-5).
4. Составьте уравнение прямой, проходящей через точки А (1;1) и В (-2;13).
5. Найдите координаты точки, принадлежащей оси абсцисс и равноудалённой от точек А(-1;4) и В(5;2).
6. Составьте уравнение прямой, которая параллельна прямой у= -2х +7 и проходит через центр окружности


Контрольная работа № 3
по теме: « Декартовы координаты »
1. Найдите длину отрезка АВ и координаты его середины, если А (-3;-4) и В (5;-2).
2. Составьте уравнение окружности, центр которой находится в точке М (1;-3) и которая проходит через точку В (-2;5).
3. Найдите координаты вершины М параллелограмма МNKF, если N(5;5), С (8;-1), D (6;-2).
4. Составьте уравнение прямой, проходящей через точки А (2;-1) и C (-3;15).
5. Найдите координаты точки, принадлежащей оси ординат и равноудалённой от точек М(-1;2) и N (5;4).
6. Составьте уравнение прямой, которая параллельна прямой у= 7х — 2 и проходит через центр окружности


Контрольная работа № 3
по теме : « Декартовы координаты»
1. Найдите длину отрезка MN и координаты его середины, если M (-4;3) и N (6;-5).
2. Составьте уравнение окружности, центр которой находится в точке F (3;-2) и которая проходит через точку N (5;-9).
3. Найдите координаты вершины C параллелограмма АВСD, если А (-3;3), B (-1;4), D (8;1).
4. Составьте уравнение прямой, проходящей через точки D (3;-4) и В (5;8).
5. Найдите координаты точки, принадлежащей оси абсцисс и равноудалённой от точек D(1;10) и K(7;8).
6. Составьте уравнение прямой, которая параллельна прямой у= -6х -1 и проходит через центр окружности


Контрольная работа № 3
по теме : « Декартовы координаты»
1. Найдите длину отрезка EF и координаты его середины, если E (-5;2) и F (7;-6).
2. Составьте уравнение окружности, центр которой находится в точке C (5;-3) и которая проходит через точку N (2;-4).
3. Найдите координаты вершины K параллелограмма EFPK, если E(3;-1), F (-3;3), P (2;-2).
4. Составьте уравнение прямой, проходящей через точки D (-3;9) и K (5;-7).
5. Найдите координаты точки, принадлежащей оси ординат и равноудалённой от точек A(-5;2) и B (-3;6).
6. Составьте уравнение прямой, которая параллельна прямой у= 4х +9 и проходит через центр окружности


Контрольная работа № 4 по теме: «Векторы»
1. Даны точки А(-3;1), В(1;-2) и С (-1;0) Найдите:
1) координаты векторов 
2)модули векторов 
3)координаты векторов 

4) скалярное произведение векторов 
5) косинус угла между векторами 
2. Начертите треугольник АВС. Постройте вектор:
1) 




3. Даны векторы 



4. На сторонах ВС и СD параллелограмма АВСD отмечены соответственно точки М и P так, что
ВМ:МС = 2:5, СР : РD = 3 :1. Выразите вектор 



5. Найдите косинус угла между векторами 










Контрольная работа № 4 по теме: «Векторы»
1. Даны точки А(2;-1), C(3;2) и D (-3;1) Найдите:
1) координаты векторов 
2)модули векторов 
3)координаты векторов 

4) скалярное произведение векторов 
5) косинус угла между векторами 
2. Начертите треугольник АВС. Постройте вектор:
1) 




3. Даны векторы 



4. На сторонах AВ и BС параллелограмма АВСD отмечены соответственно точки М и K так, что
AМ:МB = 3:4, BK : KC = 2 :3. Выразите вектор 




5. Найдите косинус угла между векторами 










Контрольная работа № 4 по теме: «Векторы»
1. Даны точки А(3;-2), В(1;-1) и С (-1;1) Найдите:
1) координаты векторов 
2)модули векторов 
3)координаты векторов 

4) скалярное произведение векторов 
5) косинус угла между векторами 
2. Начертите треугольник АВС. Постройте вектор:
1) 




3. Даны векторы 



4. На сторонах AВ и AD параллелограмма АВСD отмечены соответственно точки E и F так, что
AE:EB = 7:2, AF : FD = 5 :1. Выразите вектор 




5. Найдите косинус угла между векторами 










Контрольная работа № 4 по теме: «Векторы»
1. Даны точки А(1;5), B(-3;2) и C (2;3) Найдите:
1) координаты векторов 
2)модули векторов 
3)координаты векторов 

4) скалярное произведение векторов 
5) косинус угла между векторами 
2. Начертите треугольник DEF. Постройте вектор:
1) 




3. Даны векторы 



4. На сторонах AD и СD параллелограмма АВСD отмечены соответственно точки S и T так, что
AS:SD = 5:3, CT : TD = 2 :1. Выразите вектор 




5. Найдите косинус угла между векторами 










Контрольная работа № 5
по теме: «Геометрические преобразования»
1. Найдите координаты точек, симметричных точкам
М (-6;8) и К (0;-2) относительно: 1)оси абсцисс; 2)оси ординат;3)начала координат.
2. Начертите треугольник АВС. Постройте образ треугольника АВС:
1) при параллельном переносе на вектор 
2) при симметрии относительно точки B;
3) при симметрии относительно прямой АС.
3. Точка 
4. Прямая, параллельная стороне АС треугольника АВС, пересекает его сторону АВ в точке М, а сторону ВС в точке К. Найдите площадь трапеции АМКС, если ВМ=4 см, АМ=8 см, а площадь треугольника МВК равна 5
5. Из точек А и В, лежащих в одной полуплоскости относительно прямой а , опущены перпендикуляры 




Контрольная работа № 5
по теме: «Геометрические преобразования»
1. Найдите координаты точек, симметричных точкам
С (4;-3) и D (8;0) относительно: 1)оси ординат; 2) оси абсцисс; 3)начала координат.
2. Начертите треугольник DEF. Постройте образ треугольника DEF:
1) при параллельном переносе на вектор 
2) при симметрии относительно точки D;
3) при симметрии относительно прямой EF.
3. Точка 
4. Прямая, параллельная стороне MF треугольник MNF, пересекает его сторону MN в точке D, а сторону NF в точке К. Найдите площадь трапеции МDKF, если DK=9 см, МF=27 см, а площадь треугольника МNF равна 72
5. Из точек M и K, лежащих в одной полуплоскости относительно прямой b , опущены перпендикуляры 




Контрольная работа № 5
по теме: «Геометрические преобразования»
1. Найдите координаты точек, симметричных точкам
А (7;-9) и В (0;6) относительно: 1)оси абсцисс; 2)оси ординат;3)начала координат.
2. Начертите треугольник ВСD. Постройте образ треугольника ВСD:
1) при параллельном переносе на вектор 
2) при симметрии относительно точки B;
3) при симметрии относительно прямой BС.
3. Точка 

4. Прямая, параллельная стороне АB треугольника АВС, пересекает его сторону АC в точке F, а сторону ВС в точке D. Найдите площадь трапеции АFDB, если CD=6 см, DB=9 см, а площадь треугольника FCD равна 20
5. Из точек C и D, лежащих в одной полуплоскости относительно прямой c , опущены перпендикуляры 




Контрольная работа № 5
по теме: «Геометрические преобразования»
1.Найдите координаты точек, симметричных точкам
E (9;-5) и F (-4;0) относительно: 1)оси ординат; 2) оси абсцисс; 3)начала координат.
2. Начертите треугольник MNK. Постройте образ треугольника MNK:
1) при параллельном переносе на вектор 
2) при симметрии относительно точки K;
3) при симметрии относительно прямой NK.
3. Точка 

4. Прямая, параллельная стороне DM треугольник DKM, пересекает его сторону DK в точке P, а сторону MK в точке N. Найдите площадь трапеции DPNM, если KP=8 см, PD=20 см, а площадь треугольника DKМ равна 98
5. Из точек A и B, лежащих в одной полуплоскости относительно прямой m , опущены перпендикуляры 





Итоговая контрольная работа
Обобщение и систематизация знаний учащихся
1. Две стороны параллелограмма равны 3 см и 2 

1) большую диагональ параллелограмма;
2) площадь параллелограмма.
2. В треугольнике АВС известно, что ВС = 



3. Около правильного треугольника АВС со стороной 12 см описана окружность с центром О. 1) Найдите площадь сектора, содержащего дугу АС. 2)Какой отрезок является образом стороны ВС при повороте вокруг центра О против часовой стрелки на угол 120
4. Докажите, что четырёхугольник АВСD с вершинами в точках А (-1;-1), В(-3;1), С(1;5) и D (3;3) является прямоугольником.
5. Найдите уравнение окружности, являющейся образом окружности 


6. Найдите косинус угла между векторами 









Итоговая контрольная работа
Обобщение и систематизация знаний учащихся
1. Две стороны параллелограмма равны 4 см и 4 

1) большую диагональ параллелограмма;
2) площадь параллелограмма.
2.В треугольнике АВС известно, что АС = 



3. Около квадрата АВСD со стороной 8 см описана окружность с центром О. 1) Найдите площадь сектора, содержащего дугу BС. 2)Какой отрезок является образом стороны AD при повороте вокруг центра О против часовой стрелки на угол 90
4. Докажите, что четырёхугольник АВСD с вершинами в точках А (-3;3), В(2;4), С(1;-1) и D (-4;-2) является ромбом.
5. Найдите уравнение окружности, являющейся образом окружности 


6. Найдите косинус угла между векторами 








Итоговая контрольная работа
Обобщение и систематизация знаний учащихся
1. Две стороны параллелограмма равны 8 см и 3 см, а угол между ними — 120 
1) большую диагональ параллелограмма;
2) площадь параллелограмма.
2. В треугольнике DEF известно, что DF = 



3. Около правильного шестиугольника АВСDEF со стороной 6 см описана окружность с центром О. 1) Найдите площадь сектора, содержащего дугу СD. 2)Какой отрезок является образом стороны AВ при повороте вокруг центра О против часовой стрелки на угол 120
4. Докажите, что четырёхугольник АВСD с вершинами в точках
А (-2;2), В(-5;-1), С(-1;-5) и D (2;-2) является прямоугольником.
5. Найдите уравнение окружности, являющейся образом окружности 


6. Найдите косинус угла между векторами 









Итоговая контрольная работа
Обобщение и систематизация знаний учащихся
1. Две стороны параллелограмма равны 3 см и 4 

1) большую диагональ параллелограмма;
2) площадь параллелограмма.
2. В треугольнике DEF известно, что EF = 



3.Около правильного шестиугольника АВСDEF со стороной 3 см описана окружность с центром О. 1) Найдите площадь сектора, содержащего дугу АBС. 2)Какой отрезок является образом стороны ВС при повороте вокруг центра О против часовой стрелки на угол 60
4. Докажите, что четырёхугольник АВСD с вершинами в точках
А (3;3), В(5;-1), С(1;1) и D (-1;5) является ромбом.
5. Найдите уравнение окружности, являющейся образом окружности 


6. Найдите косинус угла между векторами 







Видео:ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Контрольная работа № 4 по теме «Векторы» (9 класс, Мерзляк А.Г. и др.)
Даны четыре варианта контрольной работы, удобно вносить изменения и печатать.
Просмотр содержимого документа
«Контрольная работа № 4 по теме «Векторы» (9 класс, Мерзляк А.Г. и др.)»
Контрольная работа № 4 по теме «Векторы»
1. Даны точки A (−3; 1), B (1; −2) и C (−1; 0). Найдите:
1) координаты векторов 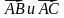
2) модули векторов 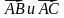
3) координаты вектора 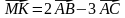
4) скалярное произведение векторов 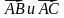
5) косинус угла между векторами 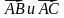
2. Начертите треугольник ABC. Постройте вектор:
1) 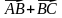
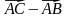
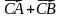
3. Даны векторы 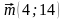
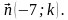
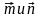
1) коллинеарны; 2) перпендикулярны?
4. На сторонах BC и CD параллелограмма ABCD отмечены соответственно точки M и P так, что BM : MC = 2 : 5, CP : PD = 3 : 1. Выразите вектор 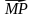
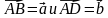
5. Найдите косинус угла между векторами 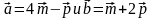
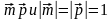
1. Даны точки A (2; −1), C (3; 2) и D (−3; 1). Найдите:
1) координаты векторов 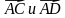
2) модули векторов 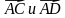
3) координаты вектора 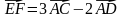
4) скалярное произведение векторов 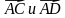
5) косинус угла между векторами 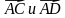
2. Начертите треугольник ABC. Постройте вектор:
1) 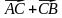
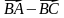
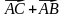
3. Даны векторы 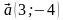
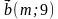
1) коллинеарны; 2) перпендикулярны?
4. На сторонах AB и BC параллелограмма ABCD отмечены соответственно точки M и K так, что AM : MB = 3 : 4, BK : KC = 2 : 3. Выразите вектор через векторы
5. Найдите косинус угла между векторами , если .
1. Даны точки A (3; −2), B (1; −1) и C (−1; 1). Найдите:
1) координаты векторов ;
2) модули векторов ;
3) координаты вектора ;
4) скалярное произведение векторов ;
5) косинус угла между векторами .
2. Начертите треугольник ABC. Постройте вектор:
3. Даны векторы и При каком значении p векторы 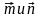
1) коллинеарны; 2) перпендикулярны?
4. На сторонах AB и AD параллелограмма ABCD отмечены соответственно точки E и F так, что AE : EB = 7 : 2, AF : FD = 5 : 1. Выразите вектор через векторы
5. Найдите косинус угла между векторами , если .
1. Даны точки A (1; 5), B (−3; 2) и C (2; 3). Найдите:
1) координаты векторов ;
2) модули векторов ;
3) координаты вектора ;
4) скалярное произведение векторов ;
5) косинус угла между векторами .
2. Начертите треугольник DEF. Постройте вектор:
3. Даны векторы и . При каком значении x векторы :
1) коллинеарны; 2) перпендикулярны?
4. На сторонах AD и CD параллелограмма ABCD отмечены соответственно точки S и T так, что AS : SD = 5 : 3, CT : TD = 2 : 1. Выразите вектор через векторы
5. Найдите косинус угла между векторами , если .
📹 Видео
Векторы. Метод координат. Вебинар | МатематикаСкачать

МЕРЗЛЯК-7 ГЕОМЕТРИЯ КОНТРОЛЬНАЯ РАБОТА-1Скачать

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

МЕРЗЛЯК-7 ГЕОМЕТРИЯ. КОНТРОЛЬНАЯ РАБОТА -2. ТРЕУГОЛЬНИКИСкачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать









