Даны четыре варианта контрольной работы, удобно вносить изменения и печатать.
- Просмотр содержимого документа «Контрольная работа № 4 по теме «Векторы» (9 класс, Мерзляк А.Г. и др.)»
- Геометрия 9 Контрольная 4 (Мерзляк)
- Геометрия 9 класс (УМК Мерзляк) Контрольная работа № 4
- Вариант 1
- Вариант 2
- Вариант 3
- Вариант 4
- Добавить комментарий Отменить ответ
- Предметы
- Новые работы
- Найти контрольную:
- Авторы работ и УМК
- Предметы
- Важные страницы
- Популярное
- Предупреждение
- Контрольная работа по геометрии 9 класс на тему » Векторы»
- «Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
- 🎬 Видео
Просмотр содержимого документа
«Контрольная работа № 4 по теме «Векторы» (9 класс, Мерзляк А.Г. и др.)»
Контрольная работа № 4 по теме «Векторы»
1. Даны точки A (−3; 1), B (1; −2) и C (−1; 0). Найдите:
1) координаты векторов 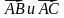
2) модули векторов 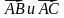
3) координаты вектора 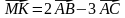
4) скалярное произведение векторов 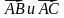
5) косинус угла между векторами 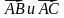
2. Начертите треугольник ABC. Постройте вектор:
1) 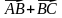
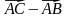
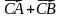
3. Даны векторы 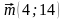
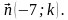
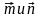
1) коллинеарны; 2) перпендикулярны?
4. На сторонах BC и CD параллелограмма ABCD отмечены соответственно точки M и P так, что BM : MC = 2 : 5, CP : PD = 3 : 1. Выразите вектор 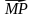
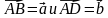
5. Найдите косинус угла между векторами 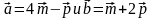
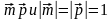
1. Даны точки A (2; −1), C (3; 2) и D (−3; 1). Найдите:
1) координаты векторов 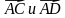
2) модули векторов 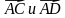
3) координаты вектора 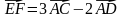
4) скалярное произведение векторов 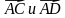
5) косинус угла между векторами 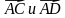
2. Начертите треугольник ABC. Постройте вектор:
1) 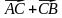
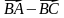
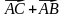
3. Даны векторы 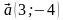
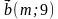
1) коллинеарны; 2) перпендикулярны?
4. На сторонах AB и BC параллелограмма ABCD отмечены соответственно точки M и K так, что AM : MB = 3 : 4, BK : KC = 2 : 3. Выразите вектор через векторы
5. Найдите косинус угла между векторами , если .
1. Даны точки A (3; −2), B (1; −1) и C (−1; 1). Найдите:
1) координаты векторов ;
2) модули векторов ;
3) координаты вектора ;
4) скалярное произведение векторов ;
5) косинус угла между векторами .
2. Начертите треугольник ABC. Постройте вектор:
3. Даны векторы и При каком значении p векторы 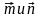
1) коллинеарны; 2) перпендикулярны?
4. На сторонах AB и AD параллелограмма ABCD отмечены соответственно точки E и F так, что AE : EB = 7 : 2, AF : FD = 5 : 1. Выразите вектор через векторы
5. Найдите косинус угла между векторами , если .
1. Даны точки A (1; 5), B (−3; 2) и C (2; 3). Найдите:
1) координаты векторов ;
2) модули векторов ;
3) координаты вектора ;
4) скалярное произведение векторов ;
5) косинус угла между векторами .
2. Начертите треугольник DEF. Постройте вектор:
3. Даны векторы и . При каком значении x векторы :
1) коллинеарны; 2) перпендикулярны?
4. На сторонах AD и CD параллелограмма ABCD отмечены соответственно точки S и T так, что AS : SD = 5 : 3, CT : TD = 2 : 1. Выразите вектор через векторы
5. Найдите косинус угла между векторами , если .
Видео:ВЕКТОРЫ. Контрольная № 4 Геометрия 9 класс.Скачать

Геометрия 9 Контрольная 4 (Мерзляк)
Геометрия 9 Контрольная 4 (Мерзляк). Контрольная работа по геометрии в 9 классе «Векторы» для УМК Мерзляк, Полонский, Якир в 4-х вариантов. Ответов нет.
Геометрия 9 класс (УМК Мерзляк)
Контрольная работа № 4
Векторы
Вариант 1
- Даны точки A (–3; 1), B (1; –2) и C (–1; 0). Найдите:
1) координаты векторов AB и AC;
2) модули векторов AB и AC;
3) координаты вектора MK = 2AB – 3AC;
4) скалярное произведение векторов AB и AC;
5) косинус угла между векторами AB и AC. - Начертите треугольник ABC. Постройте вектор:
1) AB + BC; 2) AC – AB; 3) CA + CB. - Даны векторы m (4;14) и n (–7; k). При каком значении k векторы m и n: 1) коллинеарны; 2) перпендикулярны?
- На сторонах BC и CD параллелограмма ABCD отмечены соответственно точки M и P так, что BM : MC = 2 : 5, CP : PD = 3 : 1. Выразите вектор MP через векторы AB = а и AD = b.
- Найдите косинус угла между векторами а = 4m – p и b = m + 2p, если m ⊥ p и m = |p| = 1.
Вариант 2
- Даны точки A (2; –1), C (3; 2) и D (–3; 1). Найдите:
1) координаты векторов AC и AD;
2) модули векторов AC и AD;
3) координаты вектора EF = 3AC – 2AD;
4) скалярное произведение векторов AC и AD;
5) косинус угла между векторами AC и AD. - Начертите треугольник ABC. Постройте вектор:
1) AC + CB; 2) BA – BC; 3) AC + AB. - Даны векторы а (3; – 4) и b (m; 9). При каком значении m векторы а и b: 1) коллинеарны; 2) перпендикулярны?
- На сторонах AB и BC параллелограмма ABCD отмечены соответственно точки M и K так, что AM : MB = 3 : 4, BK : KC = 2 : 3. Выразите вектор MK через векторы DA = а и DC = b.
- Найдите косинус угла между векторами m = 5а + b и n = 2а – b, если a ⊥ b и |a| = |b| = 1.
Вариант 3
- Даны точки A (3; –2), B (1; –1) и C (–1; 1). Найдите:
1) координаты векторов BA и BC;
2) модули векторов BA и BC;
3) координаты вектора MP = 4BA – BC;
4) скалярное произведение векторов BA и BC;
5) косинус угла между векторами BA и BC. - Начертите треугольник ABC. Постройте вектор:
1) CA + AB; 2) BC – BA; 3) BA + BC. - Даны векторы m (2; p) и n (9; –3). При каком значении p векторы m и n: 1) коллинеарны; 2) перпендикулярны?
- На сторонах AB и AD параллелограмма ABCD отмечены соответственно точки E и F так, что AE : EB = 7 : 2, AF : FD = 5 : 1. Выразите вектор EF через векторы CD = а и CB = b .
- Найдите косинус угла между векторами b = 6m – n и c = m + 3n, если m ⊥ n и |m| = |n| = 1.
Вариант 4
- Даны точки A (1; 5), B (–3; 2) и C (2; 3). Найдите:
1) координаты векторов CA и CB;
2) модули векторов CA и CB;
3) координаты вектора DM = 3CA – 4CB;
4) скалярное произведение векторов CA и CB;
5) косинус угла между векторами CA и CB. - Начертите треугольник DEF. Постройте вектор:
1) DE + EF; 2) ED – EF; 3) FE + FD. - Даны векторы а (x;10) и b (–5; 4). При каком значении x векторы а и b: 1) коллинеарны; 2) перпендикулярны?
- На сторонах AD и CD параллелограмма ABCD отмечены соответственно точки S и T так, что AS : SD = 5 : 3, CT : TD = 2 : 1. Выразите вектор ST через векторы BA = а и BC = b.
- Найдите косинус угла между векторами m = 3а – b и n = a + 4b, если а ⊥ b и |a| = |b| = 1.
Вы смотрели: Геометрия 9 Контрольная 4 (Мерзляк). Контрольная работа по геометрии в 9 классе «Векторы» для УМК Мерзляк, Полонский, Якир в 4-х вариантов. Цитаты из пособия «Геометрия 9 класс. Методическое пособие / Е.В. Буцко и др.» использованы в учебных целях.
Добавить комментарий Отменить ответ
Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.
Видео:РАЗБОР КОНТРОЛЬНОЙ РАБОТЫ | 9 КЛАСС ГЕОМЕТРИЯ АТАНАСЯН | ВЕКТОРЫСкачать

Предметы
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Новые работы
Видео:9 класс КОНТРОЛЬНАЯ РАБОТА №4 по ГЕОМЕТРИИ - МерзлякСкачать

Найти контрольную:
Видео:9 кл Геометрия КР№1 ВекторыСкачать

Авторы работ и УМК
Видео:Геометрия 9. Подготовка к КР по теме ВекторыСкачать

Предметы
Видео:Подготовка к контрольной работе Координаты и векторыСкачать

Важные страницы
Соглашение о конфиденциальности
(с) 2021. Дистанционный информационный Центр НПИ (г.Москва). Бесплатная помощь школьникам, находящимся на домашнем или семейном обучении. Цитаты из учебных пособий размещены в учебных целях. Контакты: kip1979@mail.ru
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Популярное
Видео:Контрольная работа №2. Геометрия. 9 класс. 2 вариант.Скачать

Предупреждение
Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie, пользовательских данных (сведения о местоположении; тип и версия ОС; тип и версия Браузера; тип устройства и разрешение его экрана; источник откуда пришел на сайт пользователь; с какого сайта или по какой рекламе; язык ОС и Браузера; какие страницы открывает и на какие кнопки нажимает пользователь; ip-адрес) в целях функционирования сайта, проведения ретаргетинга и проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.
Видео:Геометрия 9 Контрольная 4 (Мерзляк). Контрольная работа по геометрии в 9 классе «Векторы»Скачать

Контрольная работа по геометрии 9 класс на тему » Векторы»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Координаты вектора. 9 класс.Скачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
Конт рольная работа по геометрии по теме «Векторы»
1. Начертите два неколлинеарных вектора a и b . Постройте векторы, равные: а) – a /2 + 3 b ; б) 2 b – a .
2. На стороне ВС ромба ABCD лежит точка К так, что ВК = КС, О — точка пересечения диагоналей. Выразите векторы АО, АК, KD через векторы a = АВ и b = AD.
3. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 см и 12 см. Найдите среднюю линию трапеции.
4. * В треугольнике АВС точка О — точка пересечения медиан. Выразите вектор АО через векторы а = АВ и b = АС.
1. Начертите два неколлинеарных вектора m и n . Постройте векторы, равные: а) — m /3 + 2 n ; б) 3 n – m .
2. На стороне CD квадрата ABCD лежит точка Р так, что СР = PD, О – точка пересечения диагоналей. Выразите векторы ВО, ВР, РА через векторы х = ВА и у = ВС.
3. В равнобедренной трапеции один из углов равен 60°, боковая сторона равна 8 см, а меньшее основание — 7 см. Найдите среднюю линию трапеции.
4. * В треугольнике MNK точка О — точка пересечения медиан, MN = а , МК = у , МО = k (х + у) . Найдите число k .
Ответы на задачи Вариант 1
№ 2. На стороне ВС ромба ABCD лежит точка К так, что ВК = КС, О — точка пересечения диагоналей. Выразите векторы АО, АК, KD через векторы a = АВ и b = AD.
ОТВЕТ: АО = 1/2 • (а + b); АК = а + b/2; KD = b/2 – а.
№ 3. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 см и 12 см. Найдите среднюю линию трапеции.
ОТВЕТ: 12 см.
№ 4*. В треугольнике АВС точка О — точка пересечения медиан. Выразите вектор АО через векторы а = АВ и b = АС.
ОТВЕТ: а/3 + b/3.
Ответы на задачи Вариант 2
№ 2. На стороне CD квадрата ABCD лежит точка Р так, что СР = PD, О – точка пересечения диагоналей. Выразите векторы ВО, ВР, РА через векторы х = ВА и у = ВС.
ОТВЕТ: ВО = 1/2 • (x + y): BP = y + х/2; АР = у – х/2.
№ 3. В равнобедренной трапеции один из углов равен 60°, боковая сторона равна 8 см, а меньшее основание — 7 см. Найдите среднюю линию трапеции.
ОТВЕТ: 11 см.
№ 4*. В треугольнике MNK точка О — точка пересечения медиан, MN = а, МК = у, МО = k (х + у). Найдите число k.
ОТВЕТ: k = 1/3.
🎬 Видео
Контрольная работа #4. Геометрия 7 класс. Второй вариантСкачать

Контрольная работа по геометрии по теме "Метод координат". Разбор заданий. Геометрия 9 классСкачать

ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

Разбор контрольной работы по геометрии: Векторы в пространствеСкачать

9 класс. Контрольная №1 (из 6). Тема: Векторы. Подробное решение с объяснением. Пробуем свои силы!Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

9 кл Геометрия Векторы КР№1 2 уровень сложностиСкачать

Векторы. Метод координат. Вебинар | МатематикаСкачать


