Даны четыре варианта контрольной работы, удобно вносить изменения и печатать.
- Просмотр содержимого документа «Контрольная работа № 4 по теме «Векторы» (9 класс, Мерзляк А.Г. и др.)»
- ОТВЕТЫ на КР-4 Геометрия 9 Мерзляк
- ОТВЕТЫ на КР-4 Геометрия 9 Мерзляк
- Ответы на Контрольную работу № 4
- Добавить комментарий Отменить ответ
- Предметы
- Новые работы
- Найти контрольную:
- Авторы работ и УМК
- Предметы
- Важные страницы
- Популярное
- Предупреждение
- Контрольная работа по теме: «Векторы» (вариант 2)
- 📺 Видео
Просмотр содержимого документа
«Контрольная работа № 4 по теме «Векторы» (9 класс, Мерзляк А.Г. и др.)»
Контрольная работа № 4 по теме «Векторы»
1. Даны точки A (−3; 1), B (1; −2) и C (−1; 0). Найдите:
1) координаты векторов 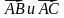
2) модули векторов 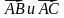
3) координаты вектора 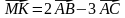
4) скалярное произведение векторов 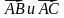
5) косинус угла между векторами 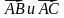
2. Начертите треугольник ABC. Постройте вектор:
1) 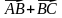
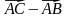
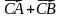
3. Даны векторы 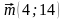
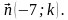
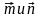
1) коллинеарны; 2) перпендикулярны?
4. На сторонах BC и CD параллелограмма ABCD отмечены соответственно точки M и P так, что BM : MC = 2 : 5, CP : PD = 3 : 1. Выразите вектор 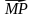
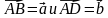
5. Найдите косинус угла между векторами 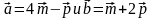
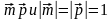
1. Даны точки A (2; −1), C (3; 2) и D (−3; 1). Найдите:
1) координаты векторов 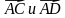
2) модули векторов 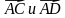
3) координаты вектора 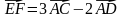
4) скалярное произведение векторов 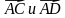
5) косинус угла между векторами 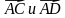
2. Начертите треугольник ABC. Постройте вектор:
1) 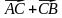
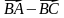
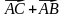
3. Даны векторы 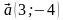
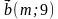
1) коллинеарны; 2) перпендикулярны?
4. На сторонах AB и BC параллелограмма ABCD отмечены соответственно точки M и K так, что AM : MB = 3 : 4, BK : KC = 2 : 3. Выразите вектор через векторы
5. Найдите косинус угла между векторами , если .
1. Даны точки A (3; −2), B (1; −1) и C (−1; 1). Найдите:
1) координаты векторов ;
2) модули векторов ;
3) координаты вектора ;
4) скалярное произведение векторов ;
5) косинус угла между векторами .
2. Начертите треугольник ABC. Постройте вектор:
3. Даны векторы и При каком значении p векторы 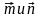
1) коллинеарны; 2) перпендикулярны?
4. На сторонах AB и AD параллелограмма ABCD отмечены соответственно точки E и F так, что AE : EB = 7 : 2, AF : FD = 5 : 1. Выразите вектор через векторы
5. Найдите косинус угла между векторами , если .
1. Даны точки A (1; 5), B (−3; 2) и C (2; 3). Найдите:
1) координаты векторов ;
2) модули векторов ;
3) координаты вектора ;
4) скалярное произведение векторов ;
5) косинус угла между векторами .
2. Начертите треугольник DEF. Постройте вектор:
3. Даны векторы и . При каком значении x векторы :
1) коллинеарны; 2) перпендикулярны?
4. На сторонах AD и CD параллелограмма ABCD отмечены соответственно точки S и T так, что AS : SD = 5 : 3, CT : TD = 2 : 1. Выразите вектор через векторы
5. Найдите косинус угла между векторами , если .
Видео:ВЕКТОРЫ. Контрольная № 4 Геометрия 9 класс.Скачать

ОТВЕТЫ на КР-4 Геометрия 9 Мерзляк
Видео:Контрольная работа №2. Геометрия. 9 класс. 2 вариант.Скачать

ОТВЕТЫ на КР-4 Геометрия 9 Мерзляк
ОТВЕТЫ на КР-4 Геометрия 9 Мерзляк — это решения и ответы на контрольную работу № 4 (в 2-х вариантах) из пособия для учащихся «Геометрия. Дидактические материалы. 9 класс ФГОС» (авт. А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, изд-во «Вентана-Граф»), которые используются в комплекте с учебником «Геометрия 9 класс» (авт. А.Г. Мерзляк, В.Б. Полонский, М.С. Якир) системы «Алгоритм успеха».
Ответы на Контрольную работу № 4
ОТВЕТЫ НА ВАРИАНТ 1
№ 1. 1) AB (3; -4); CA (-4; 1); 2) |AB| = 5; |CA| = √17; 3) 3AB – 2CA; 4) -8; 5) –(8√17)/85.
№ 2.
№ 3. 1) 9; 2) 1.
№ 4. -4a/5 – b/4.
№ 5. √2/10.
ОТВЕТЫ НА ВАРИАНТ 2
№ 1. 1) AB (3; -4); CA (-4; -1); 2) |AB| = 5; |CA| = √17; 3) (17; -10) 4) -8; 5) –(8√17)/85.
№ 2.
№ 3. 1) 9; 2) 1.
№ 4. -4a/5 – b/4.
№ 5. √2/10.
Решения и ответы на контрольную работу № 4 по Геометрии в 9 классе, которая используется в комплекте с учебником «Геометрия 9 класс» (авт. А.Г. Мерзляк, В.Б. Полонский, М.С. Якир) системы «Алгоритм успеха». Вернуться на страницу «Контрольные работы по геометрии 9 класс».
Добавить комментарий Отменить ответ
Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.
Видео:РАЗБОР КОНТРОЛЬНОЙ РАБОТЫ | 9 КЛАСС ГЕОМЕТРИЯ АТАНАСЯН | ВЕКТОРЫСкачать

Предметы
Видео:Контрольная работа 4 вариант 2Скачать

Новые работы
Видео:Контрольная работа #4. Геометрия 7 класс. Второй вариантСкачать

Найти контрольную:
Видео:Геометрия 9. Подготовка к КР по теме ВекторыСкачать

Авторы работ и УМК
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Предметы
Видео:КР № 4 В-2 - Алгебра 8 класс Мерзляк дидактические материалыСкачать

Важные страницы
Соглашение о конфиденциальности
(с) 2021. Дистанционный информационный Центр НПИ (г.Москва). Бесплатная помощь школьникам, находящимся на домашнем или семейном обучении. Цитаты из учебных пособий размещены в учебных целях. Контакты: kip1979@mail.ru
Видео:9 кл Геометрия КР№1 ВекторыСкачать

Популярное
Видео:9 кл Геометрия Векторы КР№1 2 уровень сложностиСкачать

Предупреждение
Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie, пользовательских данных (сведения о местоположении; тип и версия ОС; тип и версия Браузера; тип устройства и разрешение его экрана; источник откуда пришел на сайт пользователь; с какого сайта или по какой рекламе; язык ОС и Браузера; какие страницы открывает и на какие кнопки нажимает пользователь; ip-адрес) в целях функционирования сайта, проведения ретаргетинга и проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.
Видео:МЕРЗЛЯК-7 ГЕОМЕТРИЯ. КОНТРОЛЬНАЯ РАБОТА -2. ТРЕУГОЛЬНИКИСкачать

Контрольная работа по теме: «Векторы» (вариант 2)
КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ: «ВЕКТОРЫ» (вариант 2)
Тема: Контрольная работа по теме ”Векторы” (вариант 2)
Класс: 9 класс
Педагог: , заместитель директора по воспитательной работе, учитель математики и информатики.
Учреждение образования: МОУ Шуринская средняя общеобразовательная школа Кемеровской области
Город: Кемеровская область
Цель урока: контроль знаний учащихся
Организационный момент: объяснить цель урока. Контрольная работа (тестирование)
1. Вектором называется направленный . (отрезок)
2. Векторы называются равными, если они сонаправлены и. (их длины равны)
3. Дан треугольник АВС.





А) 









А) 





Б) 





В) 





4. ABCD — параллелограмм, О — точка пересечения диагоналей, М — середина ВС, 





А) 


А) А) 









Б) А) 









В) А) 










1. Закончи предложение.
От любой точки М можно отложить вектор, равный данному вектору, и притом только. (один)
2. Вставь пропущенное слово.
Ненулевые векторы называются коллинеарными, если они лежат на одной прямой, либо на. прямых
3. Дан треугольник АВС. Выразите через векторы 




А) 
Б) 
В) 




а) 




б) 




в) 




5. ABCD — параллелограмм, О — точка пересечения диагоналей, М — середина АВ, 








А) ABCD — параллелограмм, О — точка пересечения диагоналей, М — середина АВ, 








Б) а)









В) а)









Глава X. §1 Координаты вектора ( 2 часа)
Урок 7. Разложение вектора по двум неколлинеарным векторам.
Знать формулировку и доказательство леммы о коллинеарных векторах, и теорему о разложении по двум неколлинеарным векторам;
Уметь решать задачи, применяя полученные знания.
I. Организационный момент: назвать цели урока.
III. Объяснение нового материала:
1. Разложение вектора по двум неколлинеарным векторам.
При решении задач часто возникает необходимость выразить какой-либо вектор через уже заданные векторы. Такая операция называется разложением вектора по неколлинеарным векторам.
2. Лемма о коллинеарных векторах.
Лемма — это вспомогательное утверждение, с помощью которого доказывается следующая теорема или несколько теорем.
Теорема:Если векторы 




Так как рассматриваемые векторы, по условию коллинеарны, то они могут иметь одинаковые направления. Рассмотрим два случая, когда векторы 


1) 












📺 Видео
ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

9 класс КОНТРОЛЬНАЯ РАБОТА №4 по ГЕОМЕТРИИ - МерзлякСкачать

Контрольная работа по геометрии 9 класса номер 2, вариант 2Скачать

Контрольная работа по геометрии по теме "Метод координат". Разбор заданий. Геометрия 9 классСкачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Контрольная работа "Вектора" Задание 2Скачать

Геометрия 9 Контрольная 4 (Мерзляк). Контрольная работа по геометрии в 9 классе «Векторы»Скачать

Контрольная работа по геометрии #2. Второй вариант. 7 классСкачать

Новое задание профиля №2. Все, что нужно знать о векторах | Аня МатеманяСкачать











