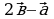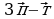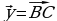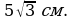Контрольная работа геометрия вектора (7 видео)

Контрольные работы по геометрии 9 кл. УМК Л.С. Атанасян

Содержание

Просмотр содержимого документа «Контрольные работы по геометрии 9 кл. УМК Л.С. Атанасян»
ГДЗ самостоятельные и контрольные работы по геометрии 9 класс Иченская Просвещение
Приоритетные группы пользователей онлайн справочника
Неоспоримые плюсы регулярной работы с учебно-практическими пособиями
Контрольные работы по геометрии (9 кл.) материал по геометрии (9 класс) по теме
Скачать:
Предварительный просмотр:
Предварительный просмотр:
Предварительный просмотр:
Предварительный просмотр:
📺 Видео

Просмотр содержимого документа
«Контрольные работы по геометрии 9 кл. УМК Л.С. Атанасян»

Контрольная работа № 1. Векторы

1. Начертите два неколлинеарных вектора и . Постройте векторы, равные:

а) ; б)

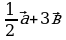
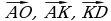
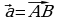
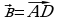
2. На стороне ВС ромба АВСD лежит точкаК такая, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы через векторы и .

3. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 и 12 см. Найдите среднюю линию трапеции.

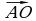
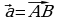
4.* В треугольнике АВС О – точка пересечения медиан. Выразите вектор через векторы и .

1. Начертите два неколлинеарных вектора 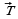и . Постройте векторы, ра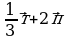вные:

а) ; б)

_2. На стороне СD квадрата АВСD лежит точка Р такая, что СР = РD , О – точка пересечения диагоналей. Выразите векторы через векторы и

3. В равнобедренной трапеции один из углов равен 60 0 , боковая сторона равна 8 см, а меньшее основание 7 см. Найдите среднюю линию трапеции.

4. * В треугольнике МNK О – точка пересечения медиан, 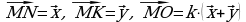. Найдите число k.

Контрольная работа № 2. Метод координат.

1. Найдите координаты и длину вектора , если .

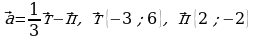
2. Напишите уравнение окружности с центром в точкеА (- 3;2), проходящей через точку В (0; — 2).

3. Треугольник МNK задан координатами своих вершин: М (- 6; 1), N (2; 4), К (2; — 2).

а) Докажите, что _Δ — равнобедренный;

б) Найдите высоту, проведённую из вершины М.

4. * Найдите координаты точки N, лежащей на оси абсцисс и равноудалённой от точек Р и К, если Р( — 1; 3 ) и К( 0; 2 ).

1). Найдите координаты и длину вектора , если .

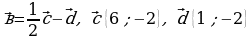
2). Напишите уравнение окружности с центром в точке С ( 2; 1 ), проходящей через точку D ( 5; 5 ).

3). Треугольник СDЕ задан координатами своих вершин: С (2; 2), D (6; 5), Е (5; — 2).

а) Докажите, что _Δ 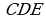— равнобедренный;

б) Найдите биссектрису, проведённую из вершины С.

4. * Найдите координаты точки А, лежащей на оси ординат и равноудалённой от точек В и С, если В( 1; — 3 ) и С( 2; 0 ).

Контрольная работа № 3.

Соотношения между сторонами и углами треугольника.

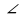
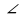
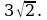
В треугольнике АВС А = 45 0 ,

В = 60 0 , ВС = Найдите АС.

Две стороны треугольника равны

7 см и 8 см, а угол между ними равен 120 0 . Найдите третью сторону треугольника.

Определите вид треугольника АВС, если

А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).

* В _ΔАВС АВ = ВС, 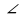САВ = 30 0 , АЕ – биссектриса, ВЕ = 8 см. Найдите площадь треугольника АВС.

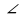
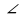
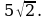
В треугольнике СDE С = 30 0 ,

D = 45 0 , СЕ = Найдите DE.

Две стороны треугольника равны

5 см и 7 см, а угол между ними равен 60 0 . Найдите третью сторону треугольника.

Определите вид треугольника АВС, если

А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).

* В ромбе АВСD АК – биссектриса угла САВ, 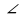ВАD = 60 0 , ВК = 12 см. Найдите площадь ромба.

Контрольная работа № 4.

Длина окружности и площадь круга.

1. Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна

2. Вычислите длину дуги окружности с радиусом 4 см, если её градусная мера равна 120 0 . Чему равна площадь соответствующего данной дуге кругового сектора?

3. Периметр правильного треугольника, вписанного в окружность, равен Найдите периметр правильного шестиугольника, описанного около той же окружности.

1. Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, описанного около него, равна 6 см.

2. Вычислите длину дуги окружности с радиусом 10 см, если её градусная мера равна 150 0 . Чему равна площадь соответствующего данной дуге кругового сектора?

3. Периметр квадрата, описанного около окружности, равен 16 дм. Найдите периметр правильного пятиугольника, вписанного в эту же окружность.

Контрольная работа № 5.

1. Начертите ромб АВСD. Постройте образ этого ромба:

а) при симметрии относительно точки С;

б) при симметрии относительно прямой АВ;

в) при параллельном переносе на вектор ;

г) при повороте вокруг точки D на 60 0 по часовой стрелке.

2. Докажите, что прямая, содержащая середины двух параллельных хорд окружности, проходит через её центр.

3. * Начертите два параллельных отрезка, длины которых равны.начертите точку, являющуюся центром симметрии, при котором один отрезок отображается на другой.

1. Начертите параллелограмм АВСD. Постройте образ этого параллелограмма:

а) при симметрии относительно точки D;

б) при симметрии относительно прямой CD;

в) при параллельном переносе на вектор ;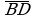

г) при повороте вокруг точки А на 45 0 против часовой стрелки.

2. Докажите, что прямая, содержащая середины противоположных сторон параллелограмма, проходит через точку пересечения его диагоналей.

3. * Начертите два параллельных отрезка, длины которых равны. Постройте центр поворота, при котором один отрезок отображается на другой.

Видео:9 кл Геометрия КР№1 ВекторыСкачать

ГДЗ самостоятельные и контрольные работы по геометрии 9 класс Иченская Просвещение

Чтобы эффективно сдать ОГЭ по математике в девятом классе, очень важно детально изучить все разделы школьной программы, которые входят в перечень экзаменационный заданий. Много сложностей у детей возникает во время обучения дисциплине геометрия. Систематически контролируя свои навыки с помощью гдз по геометрии самостоятельные и контрольные работы за 9 класс Иченская можно осуществлять самоконтроль своих знаний во время учебного года. Чтобы хорошо сдать итоговые экзамены школьник должен быть уверен в собственных силах. В учебнике упор сделан на штудирование сложных тем, которые взаимосвязаны с базовыми теоремами и аксиомами.

Видео:ВЕКТОРЫ. Контрольная № 4 Геометрия 9 класс.Скачать

Приоритетные группы пользователей онлайн справочника

Имея доступ к сборнику решений к самостоятельным и контрольным работам по геометрии для 9 класса Иченской, хорошо подготовиться и получить эффективный результат в обучении, могут следующие категории людей:

ученики девятых классов, которые в текущем году будут сдавать итоговые экзамены. Школьники смогут повторить основы геометрии, нужные правила и формулы, на основе которых придется решать задачи. После использования решебника ученик будет чувствовать себя на экзамене намного увереннее;
ребята, которые занимаются по усиленной программе с целью достичь хороших результатов в дисциплине. Можно освоить самые сложные темы досконально, чтобы поучаствовать в важном состязании и получить высокий результат;
учащиеся десятых и девятых классов, которым нужно еще раз повторить пройденные разделы, которые нужны для написания ЕГЭ;
абитуриенты, которые поступают в профильное высшее заведение, смогут воспользоваться источником в качестве справочника и сдать вступительные экзамены на высокий балл;
дети, которые обучаются на дому. Можно самостоятельно ознакомиться с темами, которые предусмотрены школьной программой;
педагоги и репетиторы, которые применяют информацию из пособия для составления интересных и ярких занятий, и оказать помощь детям, которым сложно освоить некоторые темы;
родители девятиклассников, которые не так хорошо ориентируются в дисциплине, смогут помочь ребенку, поговорив с ними о пройденной на уроке теме или проверив домашнее задание.

Видео:РАЗБОР КОНТРОЛЬНОЙ РАБОТЫ | 9 КЛАСС ГЕОМЕТРИЯ АТАНАСЯН | ВЕКТОРЫСкачать

Неоспоримые плюсы регулярной работы с учебно-практическими пособиями

Использующие решебник по геометрии к самостоятельным и контрольным работам 9 класс автор Иченская учителя и дети выделяют ряд достоинств по сравнению с другими источниками:

с помощью решебника можно хорошо сэкономить время и силы, особенно ученикам выпускных классов;
можно проверить домашнее задание перед тем, как сдать тетрадь на проверку;
все ответы оформлены в полном соответствии со структурой учебник;
доступ к решебнику есть с любого гаджета;
при низком семейном бюджете можно использовать сборник, так как он совершенно бесплатный.

Дети, которые любят математику, с удовольствием будут заниматься по индивидуальному плану с использованием решебника и осуществляя регулярный самоконтроль. Благодаря платформе еуроки ГДЗ обучение станет легким и комфортным, а количество хороших оценок в дневнике резко увеличиться.

Видео:Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

Контрольные работы по геометрии (9 кл.)
материал по геометрии (9 класс) по теме

Контрольные работы по геометриидля 9 класса ориентированы на учебник «Геометрия, 7-9» (Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.)

Видео:Разбор контрольной работы по геометрии: Векторы в пространствеСкачать

Скачать:

Вложение	Размер
k.rpogeomno19kl.doc	37 КБ
k.rpogeomno39kl.doc	659 КБ
k.r_po_geom_no49kl.doc	150 КБ
k.rpogeomno59kl.doc	162 КБ

Видео:Геометрия 9. Подготовка к КР по теме ВекторыСкачать

Предварительный просмотр:

К — 1

• 1. Начертите два неколлинеарных вектора a и b. Постройте векторы, равные: а) —- a + 3 b;

2. На стороне BC ромба ABCD лежит точка K так, что BK = KC, O – точка пересечения диагоналей. Выразите векторы AO, AK через векторы a = AB и b = AD

К — 1

• 1. Начертите два неколлинеарных вектора a и b. Постройте векторы, равные: а) —- a + 3 b;

К — 1

• 1. Начертите два неколлинеарных вектора a и b. Постройте векторы, равные: а) —- a + 3 b;

К — 1

• 1. Начертите два неколлинеарных вектора a и b. Постройте векторы, равные: а) —- a + 3 b;

• 1. Начертите два неколлинеарных вектора m и n. Постройте векторы, равные: а) —- m + 2 n;

2. На стороне CD квадрата ABCD лежит точка P так, что CP = PD, O – точка пересечения диагоналей. Выразите векторы BO, BP, PA через векторы x = BA и y = BC

3. В равнобедренной трапеции один из углов равен 60 0 , боковая сторона равна 8 см, а меньшее основание 7 см. Найдите среднюю линию трапеции.

• 1. Начертите два неколлинеарных вектора m и n. Постройте векторы, равные: а) —- m + 2 n;

Видео:ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Предварительный просмотр:

К — 3

• 1. В АВС , А = 45 , В = 60 , ВС = 3 .

2. Две стороны треугольника равны 7 см и 8 см, а

угол между ними равен 120 . Найдите третью

3. В АВС , АВ = ВС , САВ = 30 , АЕ – биссектриса,

ВЕ = 8 см. Найдите площадь треугольника АВС .

К — 3

• 1. В АВС , А = 45 , В = 60 , ВС = 3 .

2. Две стороны треугольника равны 7 см и 8 см, а

угол между ними равен 120 . Найдите третью

3. В АВС , АВ = ВС , САВ = 30 , АЕ – биссектриса,

ВЕ = 8 см. Найдите площадь треугольника АВС .

К — 3

• 1. В АВС , А = 45 , В = 60 , ВС = 3 .

2. Две стороны треугольника равны 7 см и 8 см, а

угол между ними равен 120 . Найдите третью

3. В АВС , АВ = ВС , САВ = 30 , АЕ – биссектриса,

ВЕ = 8 см. Найдите площадь треугольника АВС .

К — 3

• 1. В АВС , А = 45 , В = 60 , ВС = 3 .

2. Две стороны треугольника равны 7 см и 8 см, а

угол между ними равен 120 . Найдите третью

3. В АВС , АВ = ВС , САВ = 30 , АЕ – биссектриса,

ВЕ = 8 см. Найдите площадь треугольника АВС .

К — 3

• 1. В АВС , А = 45 , В = 60 , ВС = 3 .

2. Две стороны треугольника равны 7 см и 8 см, а

угол между ними равен 120 . Найдите третью

3. В АВС , АВ = ВС , САВ = 30 , АЕ – биссектриса,

ВЕ = 8 см. Найдите площадь треугольника АВС .

• 1. В СДЕ , С = 30 , Д = 45 , СЕ = 5 .

2. Две стороны треугольника равны 5 см и 7 см, а

угол между ними равен 60 . Найдите третью

3. В ромбе АВСД , АК – биссектрису угла САВ,

ВАД = 60 , ВК = 12 см. Найдите площадь ромба.

• 1. В СДЕ , С = 30 , Д = 45 , СЕ = 5 .

2. Две стороны треугольника равны 5 см и 7 см, а

угол между ними равен 60 . Найдите третью

3. В ромбе АВСД , АК – биссектрису угла САВ,

ВАД = 60 , ВК = 12 см. Найдите площадь ромба.

• 1. В СДЕ , С = 30 , Д = 45 , СЕ = 5 .

2. Две стороны треугольника равны 5 см и 7 см, а

угол между ними равен 60 . Найдите третью

3. В ромбе АВСД , АК – биссектрису угла САВ,

ВАД = 60 , ВК = 12 см. Найдите площадь ромба.

• 1. В СДЕ , С = 30 , Д = 45 , СЕ = 5 .

2. Две стороны треугольника равны 5 см и 7 см, а

угол между ними равен 60 . Найдите третью

3. В ромбе АВСД , АК – биссектрису угла САВ,

ВАД = 60 , ВК = 12 см. Найдите площадь ромба.

• 1. В СДЕ , С = 30 , Д = 45 , СЕ = 5 .

2. Две стороны треугольника равны 5 см и 7 см, а

угол между ними равен 60 . Найдите третью

3. В ромбе АВСД , АК – биссектрису угла САВ,

ВАД = 60 , ВК = 12 см. Найдите площадь ромба.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Предварительный просмотр:

К — 4

• 1. Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 5 см.

2. Вычислите длину дуги окружности с радиусом 4 см, если её градусная мера равна 120 . Чему равна площадь соответствующего данной дуге кругового сектора?

3. Периметр правильного треугольника, вписанного в окружность, равен 6 дм. Найдите периметр правильного шестиугольника, описанного около той же окружности.

К — 4

• 1. Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, описанного около него, равна 6 см.

2. Вычислите длину дуги окружности с радиусом 10 см, если её градусная мера равна 150 . Чему равна площадь соответствующего данной дуге кругового сектора?

3. Периметр квадрата, описанного около окружности, равен 16 дм. Найдите периметр правильного пятиугольника, вписанного в эту же окружность.

Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Предварительный просмотр:

К — 5

• 1. Начертите треугольник АВС . Постройте его образ:

при симметрии относительно его высоты, выходящей из вершины А ;
при симметрии относительно точки D , являющейся серединой стороны АВ ;
при параллельном переносе на вектор АМ , где М – точка пересечения медиан треугольника;
при повороте вокруг вершины С на 45 против часовой стрелки.