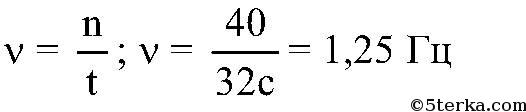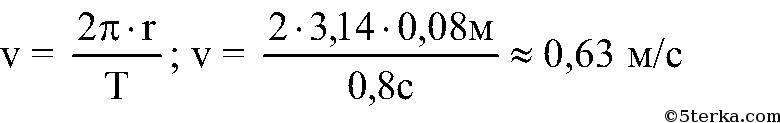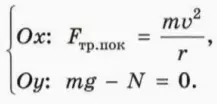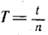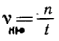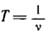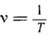Конический маятник движение по окружности

Видео:Конический маятник представляет собой маленький шарик, закрепленный на нити - №22706Скачать

Цель работы: Изучить равномерное движение по окружности и определить его основные характеристики: частоту, период, скорость и центростремительное ускорение.

Мы знаем из учебника (стр.15-16), что при равномерном движении по окружности скорость частицы не меняется по величине. На самом же деле с физической точки зрения это движение ускоренное, так как направление скорости непрерывно меняется во времени. При этом скорость в каждой точке практически направлена по касательной (рис. 9 в учебнике на стр. 16). В этом случае ускорение характеризует быстроту изменения направления скорости. Оно все время направлено к центру окружности, по которой движется частица. По этой причине его принято называть центростремительным ускорением.

Это ускорение можно вычислить по формуле:

Быстроту движения тела по окружности характеризуют числом полных оборотов, совершаемых в единицу времени. Это число называется частотой вращения. Если тело делает v оборотов в секунду, то время, за которое совершается один оборот,

секунд. Это время называется периодом вращения

Чтобы вычислить скорость движения тела по окружности, надо путь, проходимый телом за один оборот, (он равен длине

окружности) поделить на период:

в этой работе мы

будем наблюдать за движением шарика, подвешенного на ните и движущегося по окружности.

Пример выполнения работы:

Вывод: Входе проделанного эксперимента были определены:

1) Период Т = 0,8с;

2) Частота v = 1,25 Гц;

3) Скорость при равномерном движении по окружности v = 0,63м/с

4) Центростремительное ускорение а = 5м/с 2 .

Решебник по физике за 7 класс (С.В Громов, Н.А. Родина, 2000 год),
задача №2
к главе «Лабораторные работы».

Видео:Физика в школе Движение по окружности КОНИЧЕСКИЙ МАЯТНИК ЕГЭ ГИАСкачать

Движение по окружности под действием нескольких сил

1. Поворот транспорта

Движение по горизонтальной дороге

Напомним, что ускорение тела, движущегося со скоростью v по окружности радиусом r, направлено к центру окружности (центростремительное ускорение). Модуль ускорения

Согласно второму закону Ньютона

= m,

где – равнодействующая всех приложенных к телу сил.

Пусть автомобиль совершает поворот на горизонтальной дороге, двигаясь равномерно по дуге окружности. На него действуют сила тяжести m и сила нормальной реакции (рис. 21.1). Но обе они направлены вертикально и поэтому не могут вызвать ускорения, направленного горизонтально. Это ускорение вызывает горизонтально направленная сила трения, действующая на автомобиль со стороны дороги.

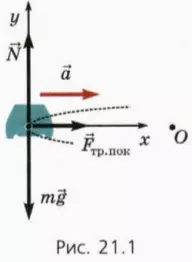
Если колеса автомобиля не проскальзывают, то нижние точки колес покоятся относительно дороги. Следовательно, ускорение вызывает сила трения покоя _тр.пок (рис. 21.1). (Эта сила возникает, когда вследствие поворота руля оси вращения передних колес поворачиваются. Причины появления этой силы можно объяснить, только рассматривая автомобиль не как материальную точку.)

? 1. Используя рисунок 21.1, объясните смысл следующих уравнений:

? 2. Чему равен радиус окружности r, по которой может равномерно двигаться автомобиль на горизонтальной дороге со скоростью v, если коэффициент трения между колесами и дорогой равен μ?
Подсказка. F_тр.пок ≤ μN.

? 3. С какой наибольшей скоростью (в километрах в час) автомобиль может совершить поворот на перекрестке нешироких улиц, двигаясь по дуге окружности радиусом 10 м? Рассмотрите движение автомобиля по сухому асфальту и по льду.

Выполнив это задание, вы лучше поймете, почему водитель притормаживает перед поворотом, особенно на скользкой дороге.

Движение по наклонной дороге

Если полотно дороги наклонить в сторону поворота, то сила нормальной реакции опоры будет наклонена под углом к вертикали (рис. 21.2).

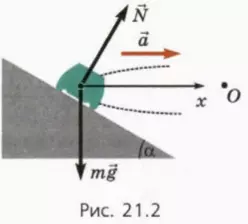
В таком случае появляется горизонтальная составляющая силы нормальной реакции, направленная в сторону поворота. Это позволяет увеличить скорость на повороте при тех же значениях радиуса поворота и коэффициента трения.

? 4. При каком угле наклона дороги автомобиль, который едет со скоростью v = 72 км/ч по дуге окружности радиусом r = 30 м, может совершить поворот даже на очень скользкой дороге?
Подсказка. В данном случае проекция силы нормальной реакции на ось x равна mg tg α.

? 5. Почему велотреки делают с наклоном внутрь (рис. 21.3)?

Гонки по вертикальной стене

Ехать по окружности можно и по вертикальной стене (рис. 21.4)! В таком случае центростремительное ускорение обеспечивает только сила нормальной реакции (рис. 21.5). (Автомобиль, который едет по вертикальной стене, не переворачивается потому, что на его нижние колеса стена давит с большей силой, чем на верхние.)

? 6. С какой скоростью (в километрах в час) можно ехать по вертикальной цилиндрической стене радиусом 5 м, если коэффициент трения μ между колесами и стеной равен 0,5?

2. Конический маятник

Подвешенный на нити груз, который равномерно движется по окружности в горизонтальной плоскости, называют коническим маятником (рис. 21.6).

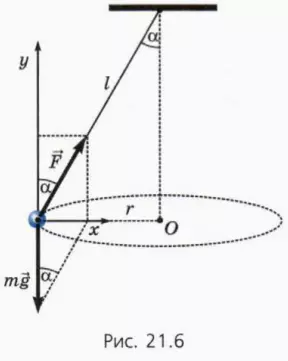
На груз действуют сила тяжести m и сила натяжения нити , направленная вдоль нити. (Силу натяжения нити в данном случае неудобно обозначать , потому что буквой T обозначен период обращения груза по окружности.) Равнодействующая этих сил вызывает центростремительное ускорение груза.

Введем обозначения:
l — длина нити,
r — радиус окружности,
α — угол между нитью и вертикалью,
T — период обращения груза по окружности.

? 7. Используя рисунок 21.6, объясните смысл следующих уравнений:

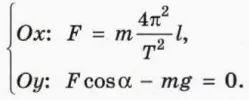
Подсказка. Воспользуйтесь тем, что r = l cos α.

? 8. Чему равен период обращения конического маятника, если длина нити равна l?

? 9. Шарик массой 100 г, подвешенный на нити длиной 50 см, вращается по окружности в горизонтальной плоскости. При этом сила натяжения нити 2 Н.
а) Какой угол составляет нить с вертикалью?
б) Чему равен период обращения шарика по окружности?
в) Чему равен радиус окружности, по которой движется шарик?
г) С какой скоростью движется шарик?
д) Во сколько раз ускорение шарика больше ускорения свободного падения?
е) За какое время шарик пройдет путь, равный 1 км?

Движение по гладкой поверхности

Пусть небольшая шайба скользит по горизонтальной окружности внутри гладкой полусферы (рис. 21.7).

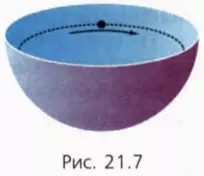
Главное в таких задачах – увидеть, что это видоизмененный конический маятник: роль силы натяжения нити играет сила нормальной реакции.

? 10. Шайба массой 50 г движется со скоростью 2 м/с по горизонтальной окружности радиусом 20 см внутри гладкой полусферы.
а) С каким ускорением движется шайба?
б) Под каким углом к вертикали направлена сила нормальной реакции, действующая на шайбу со стороны полусферы?
в) Чему равна сила нормального давлениям?
г) Чему равен радиус полусферы?
д) Чему равна частота обращения шайбы по окружности?

Рассмотрим также движение тела по внутренней поверхности конуса.

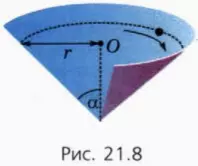
? 11. Шайба движется по горизонтальной окружности радиусом r по гладкой поверхности конуса (рис. 21.8, для наглядности конус разрезан). Образующая конуса составляет угол α с вертикалью. Чему равен период обращения шайбы?

Дополнительные вопросы и задания

12. На горизонтальном диске на расстоянии 10 см от оси лежит небольшая шайба массой 20 г. Диск начинают вращать вокруг его оси, медленно увеличивая частоту обращения. Когда частота становится равной 1 с-1, шайба начинает скользить по диску.
а) Каков коэффициент трения между шайбой и диском?
б) Чему равна сила трения, действующая на шайбу, при частоте обращения 0,5 с -1 ?
в) Начертите примерный график зависимости силы трения от частоты обращения диска.

13. Груз массой 100 г, подвешенный на пружине жесткостью 200 Н/м, вращают по окружности, лежащей в горизонтальной плоскости. Чему равна частота обращения, если длина пружины в 2 раза больше ее длины в недеформированном состоянии?

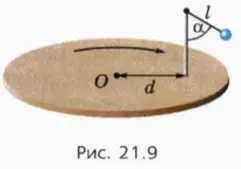
14. На стержне, укрепленном на расстоянии d от оси вращения горизонтального диска, на нити длиной l подвешен шарик (рис. 21.9). При вращении диска нить отклоняется от вертикали на угол α.
а) Каково ускорение шарика?
б) Каков период обращения диска?

Видео:Движение тела по окружности. Конический маятник.Многоуровневая задачаСкачать

Лабораторная работа «Изучение движения конического маятника» 8 класс

Лабораторная работа № 3

Тема: Изучение движения конического маятника

Цель: научиться определять период, частоту, скорость и ускорение при движении конического маятника

Оборудование: Штатив с муфтой и кольцом, шарик, нить, секундомер, лист бумаги с начерченной на нём окружностью радиусом R = 8 см

1.Подготовьте таблицу для записи измерений и вычислений

2.Привяжите нить к шарику, после чего подвесьте его к кольцу

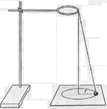
3.Взявшись двумя пальцами за нить у точки подвеса, заставьте шарик двигаться по окружности, заранее нарисованной на листе бумаги. Это и есть конический маятник.

4.Измерьте время t , за которое маятник совершит n =40 оборотов

5.Занесите в таблицу значения величин

6.Посчитайте по формулам значения величин:

7.Сравните полученные значения, через формулы:

8.Выразите и определите скорость из формулы:

🎦 Видео

Задача о коническом маятникеСкачать

Движение тела по окружности. Конический маятник ЗАДАЧА 8Скачать

ЕГЭ Физика Задание 4 #19721Скачать

Движение тела по окружности Конический маятник ЗАДАЧА 9Скачать

Выполнялка 74-Конический маятникСкачать

Конический маятникСкачать

Урок 90. Движение по окружности (ч.2)Скачать

Задача на конический маятникСкачать

Урок 89. Движение по окружности (ч.1)Скачать

Урок 92 (осн). Колебательное движение. МаятникиСкачать

Конический маятник представляет собой маленький грузик массой m=100 г, вращающийся с - №31029Скачать

Конический маятник.Решение задачСкачать

Физика - движение по окружностиСкачать

Конический маятник.Решение задач 2023-5Скачать

Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать