Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.
Переменным током (напряжением, ЭДС и т.д.) называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, — периодом Т. Для периодического тока имеем
 , , | (1) |
Величина, обратная периоду, есть частота, измеряемая в герцах (Гц):
 , , | (2) |
Диапазон частот, применяемых в технике: от сверхнизких частот (0.01 ¸ 10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .
Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:
i — мгновенное значение тока 
u – мгновенное значение напряжения 
е — мгновенное значение ЭДС 
р — мгновенное значение мощности 
Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m ) .



Действующее значение переменного тока
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:
 , , | (3) |
Аналогично определяются действующие значения ЭДС и напряжения.
Синусоидально изменяющийся ток
Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.
Изображение синусоидальных ЭДС, напряжений
и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е1 и е2 соответствуют уравнения:



Значения аргументов синусоидальных функций 





Величину 


При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.
Для синусоидальных ЭДС е1 и е2 угол сдвига фаз:

Векторное изображение синусоидально
изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е1 и е2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени ( t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
Пусть, например, в точке разветвления цепи (рис. 5) общий ток 



Каждый из этих токов синусоидален и может быть представлен уравнением


Результирующий ток также будет синусоидален:

Определение амплитуды 

На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов для t =0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным 
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

Построение векторной диаграммы в масштабе позволяет определить значения 



Представление синусоидальных ЭДС, напряжений
и токов комплексными числами
Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.
Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в :
показательной
тригонометрической 
алгебраической 
Например, ЭДС 

Фазовый угол 

В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:
 , , | (4) |
Комплексное число 
 , , | (5) |
Параметр 


Параметр 
Вообще говоря, умножение вектора на оператор поворота 
Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака “j” произведения комплекса амплитуды 


Переход от одной формы записи синусоидальной величины к другой осуществляется с помощью формулы Эйлера:
 , , | (6) |
Если, например, комплексная амплитуда напряжения задана в виде комплексного числа в алгебраической форме:

— то для записи ее в показательной форме, необходимо найти начальную фазу 


Тогда мгновенное значение напряжения:

где 
При записи выражения для определенности было принято, что 


 , , | (7) |
а при 
 | (8) |
 | (9) |
Если задано мгновенное значение тока в виде 

Следует указать, что при сложении и вычитании комплексов следует пользоваться алгебраической формой их записи, а при умножении и делении удобна показательная форма.
Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами. Так при определении комплексной амплитуды результирующего тока 

где 

Действующее значение синусоидальных ЭДС, напряжений и токов
В соответствии с выражением (3) для действующего значения синусоидального тока запишем:

Аналогичный результат можно получить для синусоидальных ЭДС и напряжений. Таким образом, действующие значения синусоидальных тока, ЭДС и напряжения меньше своих амплитудных значений в 
 . . | (10) |
Поскольку, как будет показано далее, энергетический расчет цепей переменного тока обычно проводится с использованием действующих значений величин, по аналогии с предыдущим введем понятие комплекса действующего значения

1. Основы теории цепей: Учеб. для вузов /Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
1. Какой практический смысл имеет изображение синусоидальных величин с помощью векторов?
2. Какой практический смысл имеет представление синусоидальных величин с использованием комплексных чисел?
3. В чем заключаются преимущества изображения синусоидальных величин с помощью комплексов по сравнению с их векторным представлением?
4. Для заданных синусоидальных функций ЭДС и тока 
5. На рис. 5 


Ответ: 
- Комплексные числа
- Алгебраическая форма записи комплексных чисел
- Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме
- Комплексно сопряженные числа
- Модуль комплексного числа
- Деление комплексных чисел, записанных в алгебраической форме
- Изображение комплексных чисел радиус-векторами координатной плоскости
- Аргумент комплексного числа
- Формула Эйлера. Экспоненциальная форма записи комплексного числа
- Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме
- Извлечение корня натуральной степени из комплексного числа
- Комплексная форма записи вектора
- 🌟 Видео
Видео:Тригонометрическая форма комплексного числаСкачать

Комплексные числа
 Алгебраическая форма записи комплексных чисел Алгебраическая форма записи комплексных чисел |
 Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме |
 Комплексно сопряженные числа Комплексно сопряженные числа |
 Модуль комплексного числа Модуль комплексного числа |
 Деление комплексных чисел, записанных в алгебраической форме Деление комплексных чисел, записанных в алгебраической форме |
 Изображение комплексных чисел радиус-векторами на координатной плоскости Изображение комплексных чисел радиус-векторами на координатной плоскости |
 Аргумент комплексного числа Аргумент комплексного числа |
 Тригонометрическая форма записи комплексного числа Тригонометрическая форма записи комплексного числа |
 Формула Эйлера. Экспоненциальная форма записи комплексного числа Формула Эйлера. Экспоненциальная форма записи комплексного числа |
 Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме |
 Извлечение корня натуральной степени из комплексного числа Извлечение корня натуральной степени из комплексного числа |
Видео:10 класс, 34 урок, Тригонометрическая форма записи комплексного числаСкачать

Алгебраическая форма записи комплексных чисел
Пусть x и y — произвольные вещественные числа.
Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.
Множество комплексных чисел является расширением множества вещественных чисел, поскольку множество вещественных чисел содержится в нём в виде пар (x, 0) .
Комплексные числа, заданные парами (0, y) , называют чисто мнимыми числами .
Для комплексных чисел существует несколько форм записи: алгебраическая форма записи, тригонометрическая форма записи и экспоненциальная (показательная) форма записи .
Алгебраическая форма — это такая форма записи комплексных чисел, при которой комплексное число z, заданное парой вещественных чисел (x, y) , записывается в виде
| z = x + i y . | (1) |
где использован символ i , называемый мнимой единицей .
Число x называют вещественной (реальной) частью комплексного числа z = x + i y и обозначают Re z .
Число y называют мнимой частью комплексного числа z = x + i y и обозначают Im z .
Комплексные числа, у которых Im z = 0 , являются вещественными числами .
Комплексные числа, у которых Re z = 0 , являются чисто мнимыми числами .
Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.
Видео:Математика без Ху!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.Скачать

Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме
Умножение комплексных чисел z1 = x1 + i y1 и z2 = x2 + i y2 , так же, как и операции сложения и вычитания, осуществляется по правилам умножения двучленов (многочленов), однако при этом учитывается важнейшее равенство, имеющее вид:
| i 2 = – 1 . | (2) |
По этой причине
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Комплексно сопряженные числа
Два комплексных числа z = x + iy и 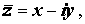
Операция перехода от комплексного числа к комплексно сопряженному с ним числу называется операцией комплексного сопряжения , обозначается горизонтальной чертой над комплексным числом и удовлетворяет следующим свойствам:
 |  |
 |  |
 |  |
 |  |
 |  |
Видео:Изображение комплексных чисел. Модуль комплексного числа. 11 класс.Скачать

Модуль комплексного числа
Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое | z | и определенное по формуле
Для произвольного комплексного числа z справедливо равенство:
а для произвольных комплексных чисел z1 и z2 справедливы неравенства:
 |  |
 |  |
 |  |
 |  |
Замечание . Если z — вещественное число, то его модуль | z | равен его абсолютной величине.
Видео:Координаты вектора. 9 класс.Скачать

Деление комплексных чисел, записанных в алгебраической форме
Деление комплексного числа z1 = x1 + i y1 на отличное от нуля комплексное число z2 = x2 + i y2 осуществляется по формуле
Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:
Деление на нуль запрещено.
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Изображение комплексных чисел радиус-векторами координатной плоскости
Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.
Назовем рассматриваемую плоскость комплексной плоскостью , и будем представлять комплексное число z = x + i y радиус–вектором с координатами (x , y).
Назовем ось абсцисс Ox вещественной осью , а ось ординат Oy – мнимой осью .
При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.
Видео:КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Аргумент комплексного числа
Рассмотрим радиус–вектор произвольного, но отличного от нуля, комплексного числа z .
Аргументом комплексного числа z называют угол φ между положительным направлением вещественной оси и радиус-вектором z .
Аргумент комплексного числа z считают положительным, если поворот от положительного направления вещественной оси к радиус-вектору z происходит против часовой стрелки, и отрицательным — в случае поворота по часовой стрелке (см. рис.).
Считается, что комплексное число нуль аргумента не имеет.
Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где k — произвольное целое число, то вводится, главное значение аргумента , обозначаемое arg z и удовлетворяющее неравенствам:
Тогда оказывается справедливым равенство:
Если для комплексного числа z = x + i y нам известны его модуль r = | z | и его аргумент φ , то мы можем найти вещественную и мнимую части по формулам
 | (3) |
Если же комплексное число z = x + i y задано в алгебраической форме, т.е. нам известны числа x и y , то модуль этого числа, конечно же, определяется по формуле
 | (4) |
а аргумент определяется в соответствии со следующей Таблицей 1.
Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.
Таблица 1. – Формулы для определения аргумента числа z = x + i y
| Расположение числа z | Знаки x и y | Главное значение аргумента | Аргумент | Примеры |
| Положительная вещественная полуось | 0 | φ = 2kπ |  | |
| Первый квадрант |  |  |  | |
| Положительная мнимая полуось |  |  |  | |
| Второй квадрант |  |  |  | |
| Отрицательная вещественная полуось | Положительная вещественная полуось | |||
| Знаки x и y | ||||
| Главное значение аргумента | 0 | |||
| Аргумент | φ = 2kπ | |||
| Примеры |  |
| Расположение числа z | Первый квадрант |
| Знаки x и y | |
| Главное значение аргумента |  |
| Аргумент |  |
| Примеры |  |
| Расположение числа z | Положительная мнимая полуось |
| Знаки x и y | |
| Главное значение аргумента |  |
| Аргумент |  |
| Примеры |  |
| Расположение числа z | Второй квадрант |
| Знаки x и y | |
| Главное значение аргумента |  |
| Аргумент |  |
| Примеры |  |
| Расположение числа z | Отрицательная вещественная полуось | ||||||||||
| Знаки x и y | Третий квадрант | ||||||||||
| Знаки x и y | Отрицательная мнимая полуось | ||||||||||
| Знаки x и y | Четвёртый квадрант | ||||||||||
| Знаки x и y | |||||||||||
| z = r (cos φ + i sin φ) , | (5) |
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .
Запись комплексного числа в форме (5) называют тригонометрической формой записи комплексного числа .
Видео:4. Показательная форма комплексного числаСкачать

Формула Эйлера. Экспоненциальная форма записи комплексного числа
В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера :
| cos φ + i sin φ = e iφ . | (6) |
Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде
| z = r e iφ , | (7) |
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .
Запись комплексного числа в форме (7) называют экспоненциальной (показательной) формой записи комплексного числа .
Из формулы (7) вытекают, в частности, следующие равенства:
а из формул (4) и (6) следует, что модуль комплексного числа
или, что то же самое, числа e iφ , при любом значении φ равен 1.
Видео:1.2 Комплексные числа и их представление векторами на комплексной плоскостиСкачать

Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме
Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.
Действительно, умножение и деление двух произвольных комплексных чисел 

Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.
При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.
Возведение комплексного числа z = r e iφ в натуральную степень осуществляется по формуле
Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Извлечение корня натуральной степени из комплексного числа
Пусть 
Корнем n — ой степени из числа z0 , где 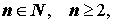
| z n = z0 . | (8) |
Для того, чтобы решить уравнение (8), перепишем его в виде
и заметим, что два комплексных числа, записанных в экспоненциальной форме, равны тогда и только тогда, когда их модули равны, а разность аргументов равна 2kπ , где k — произвольное целое число. По этой причине справедливы равенства
следствием которых являются равенства
 | (9) |
Из формул (9) вытекает, что уравнение (8) имеет n различных корней
 | (10) |
причем на комплексной плоскости концы радиус-векторов zk при k = 0 , . , n – 1 располагаются в вершинах правильного n — угольника, вписанного в окружность радиуса 
Замечание . В случае n = 2 уравнение (8) имеет два различных корня z1 и z2 , отличающихся знаком:
Пример 1 . Найти все корни уравнения
то по формуле (10) получаем:
Пример 2 . Решить уравнение
Решение . Поскольку дискриминант этого квадратного уравнения отрицателен, то вещественных корней оно не имеет. Для того, чтобы найти комплексные корни, выделим, как и в вещественном случае, полный квадрат:
Видео:Экспоненциальная запись комплексного числаСкачать
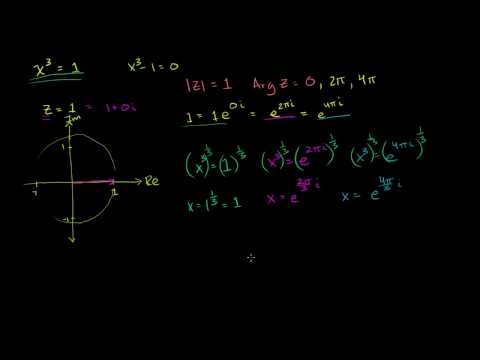
Комплексная форма записи вектора
Комплексным числом называется выражение вида z = x + iy , (7.1)
где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для мнимой единицы
Если x =0, то число 0+ iy = iy называется чисто мнимым; если y =0, то число x + i ∙0= x отождествляется с действительным числом x , а это означает, что множество R всех действительных чисел является подмножеством множества C всех комплексных чисел, то есть 
Число x называется действительной частью комплексного числа z и обозначается x = Re z , а y – мнимой частью комплексного числа z и обозначается y = Im z .
Понятия «больше» и «меньше» для комплексных чисел не вводятся.
Числа z = x + iy и 
Всякое комплексное число z = x + iy можно изобразить точкой M ( x ; y ) плоскости x 0 y такой, что x = Re z , y = Im z . Верно и обратное: каждую точку M ( x ; y ) координатной плоскости можно рассматривать как образ комплексного числа z = x + iy (рис. 7.1).
Комплексное число z = x + iy можно задавать с помощью радиус-вектора 


Для комплексного числа z =0 аргумент не определен. Аргумент комплексного числа 

Алгебраической формой комплексного числа называется з апись числа z в виде z = x + iy.
Модуль r и аргумент φ можно рассматривать как полярные координаты вектора 
Равенство (7.3) есть тригонометрическая форма комплексного числа. Модуль r = |z| однозначно определяется по формуле
Аргумент определяется из формул:
При переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить главное значение аргумента комплексного числа z , то есть считать φ= arg z . Знаки полученных значений cos φ и sin φ по формулам (7.5), дают возможность определить, какой координатной четверти принадлежит угол φ.
Используя формулу Эйлера
комплексное число 
где r =| z | — модуль комплексного числа, а угол 
Функция e i φ – периодическая с основным периодом 2 π, поэтому для записи комплексного числа в показательной форме по формуле 7.7 достаточно найти главное значение его аргумента, то есть считать φ = arg z .
Пример 7.1. Записать комплексные числа 
Решение. Для z 1 имеем 

Для действительного числа 
На множестве комплексны х чисел определен ряд операций.
Из равенства (7.9) следует, что геометрически комплексные числа вычитаются как векторы. При этом число z = z 1 – z 2 изображается вектором, соединяющим концы векторов 


Из (7.11) следует важнейшее соотношение i 2 = –1. Действительно,
Найдем произведение комплексных чисел 

Видно, что при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. Нетрудно видеть, что если есть n множителей и все они одинаковые, то частным случаем равенства (7.12) является формула возведения комплексного числа в натуральную степень:
(7.13) называется первой формулой Муавра.
Произведение двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
4. Частным двух комплексных чисел z 1 и 


Пусть 
На практике при нахождении частного двух комплексных чисел удобно умножить числитель и знаменатель дроби 
Деление комплексных чисел осуществляется также и в тригонометрической форме, при этом имеет место формула:
Видно, что при делении комплексных чисел их модули делятся, а аргументы вычитаются соответственно.
Частное двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
Пример 7.2. Найти сумму, разность, произведение и частное комплексных чисел 
Решение. По формуле (7.8) сумма заданных чисел равна 
Согласно формуле (7.9) разность заданных чисел равна 
Пользуясь формулой (7.11), вычислим их произведение
На основании формулы (7.14) вычислим их частное
Пример 7.3. Найти произведение и частное комплексных чисел 
Решение. Используя (7.4) и (7.5), получаем:
Аналогично, для z 2 можно записать:
По формулам (7.12) и (7.16) получим в тригонометрической форме:
Пользуясь формулами (7.14) и (7.17), получим в показательной форме:
5. Извлечение корня n -ой степени – операция, обратная возведению
в натуральную степень, определенному ранее формулой (7.13).
Корнем n -ой степени из комплексного числа z называется комплексное число ω, удовлетворяющее равенству ω n = z , то есть 
Пусть 



(7.18) называется второй формулой Муавра.
Видно, что для любого 
Пример 7.4. Найти все корни уравнения z 4 +16=0.
Решение. Запишем уравнение в виде z 4 =–16+0∙ i . Отсюда по формуле (7.18) получим:
Сформулируем несколько иначе основную теорему алгебры 3.2 над полем комплексных чисел .
Теорема 7.1 (основная теорема алгебры). Для всякого многочлена с комплексными коэффициентами
Приведем еще одну теорему, имеющую место над множеством комплексных чисел.
Теорема 7.2. Если многочлен Pn ( x ) с действительными коэффициентами имеет комплексный корень a + ib , то он имеет и сопряженный корень a – ib
В разложение многочлена 

Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.
🌟 Видео
Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

Математика это не ИсламСкачать

2. Геометрическая интерпретация комплексных чисел. Модуль и аргумент комплексного числаСкачать

➡️ КАК ВЫЧИТАТЬ ВЕКТОРЫ?Скачать

Показательная форма комплексного числаСкачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Как разложить вектор по базису - bezbotvyСкачать






































