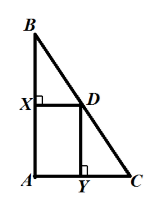Четыре точки окружности замечательные (6 видео)

Замечательные точки окружности. I. Математический диктант Вариант 1 1. Биссектрисой треугольника называется … 2. Высотой треугольника называется … 3. — презентация

Презентация была опубликована 8 лет назад пользователемВиталий Недоплясов

Содержание

Похожие презентации
Презентация на тему: » Замечательные точки окружности. I. Математический диктант Вариант 1 1. Биссектрисой треугольника называется … 2. Высотой треугольника называется … 3.» — Транскрипт:
Презентация по геометрии на тему»Четыре замечательные точки»(8класс)
«Управление общеобразовательной организацией: новые тенденции и современные технологии»
Дистанционное обучение как современный формат преподавания
Математика: теория и методика преподавания в образовательной организации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Оставьте свой комментарий
Подарочные сертификаты
Четыре замечательные точки треугольника
Точка пересечения медиан треугольника
Точка пересечения биссектрис треугольника
Готовые работы на аналогичную тему
Точка пересечения серединных перпендикуляров треугольника
Точка пересечения высот треугольника
Пример задачи на использование 4 замечательных точек треугольника
📺 Видео

Презентация на тему: » Замечательные точки окружности. I. Математический диктант Вариант 1 1. Биссектрисой треугольника называется … 2. Высотой треугольника называется … 3.» — Транскрипт:

1 Замечательные точки окружности

2 I. Математический диктант Вариант 1 1. Биссектрисой треугольника называется … 2. Высотой треугольника называется … 3. Если точка пересечения серединных перпендикуляров сторон треугольника находится вне его, то … 4. Треугольник имеет … медиан. Вариант 2 1. Медианой треугольника называется … 2. Серединным перпендикуляром стороны треугольника называется … 3. Если точка пересечения серединных перпендикуляров сторон треугольника находится на его стороне, то … 4. Треугольник имеет … биссектрис.

3 Новый материал Изобразим треугольник ABC: а) остроугольный; б) прямоугольный; в) тупоугольный. Проведем все его высоты. Сделаем соответствующее предположение и докажем следующую теорему.

4 Теорема. Высоты треугольника или их продолжения пересекаются в одной точке (ортоцентре треугольника).

5 Доказательство. Через вершины данного треугольника АВС проведем прямые, параллельные противоположным сторонам.

7 Заметим, что высоты треугольника могут не пересекаться. Изображен тупоугольный треугольник ABC, в котором продолжения высот AA1, BB1, CC1 пересекаются в одной точке H, а сами высоты не пересекаются. не пересекаются.

8 Задание Изобразим треугольник ABC: а) остроугольный; б) прямоугольный; в) тупоугольный. Проведем все его медианы. Сделаем соответствующее предположение о том, что все медианы треугольника пересекаются в одной точке. Теперь измерим все медианы от вершины до точки пересечения всех медиан, и от этой точки до соответствующей стороны. Сделаем предположение об отношении, в котором делит каждую медиану точка их пересечения и докажем следующую теорему.

9 Теорема. Медианы треугольника пересекаются в одной точке (центроиде треугольника), и делятся в этой точке в отношении 2:1, считая от вершин.

10 Доказательство. В треугольнике АВС проведем медианы АD и ВЕ и их точку пересечения обозначим через О. Отрезок ED будет средней линией треугольника АВС. Проведем среднюю линию HG в треугольнике АВО. Треугольники HGO и EDO равны (по второму признаку равенства треугольников). Следовательно, HO=OE и GO=OD. Таким образом, имеем AG=GO=OD, BH=HO=OE, т.е. медианы АD и BE в точке пересечения делятся в отношении 2:1, считая от соответствующей вершины. Медиана, проведенная из вершины С, также должна делить медиану АD в отношении 2:1. Следовательно, она будет проходить через точку О, т.е. все три медианы будут пересекаться в одной точке.

14 VI. Задание на дом 1. Выучить разобранную на уроке теорию (п. 38 учебника). 2. Решить задачи.7,8,11,22,23

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Презентация по геометрии на тему»Четыре замечательные точки»(8класс)

Видео:Урок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Четыре замечательные точки треугольника высоты биссектрисы серединные перпендикуляры медианы ГБОУ Школа 1504 Москва-2020 Учитель математики Приходько С.Н.

Биссектрисой (АD) треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. C БИССЕКТРИСА A D В

Медианой (BD) треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. А В С D Медиана

ВЫСОТА Высотой (СD) треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону. A B C D

СЕРЕДИННЫЙ ПЕРПЕНДИКУЛЯР Серединным перпендикуляром (DF) к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему(с.174,п.75) А D F B C

План занятия Теорема биссектрисы угла Свойство о биссектрисах треугольника Теорему о серединном перпендикуляре к отрезку Свойство о серединных перпендикулярах к сторонам треугольника Свойство медиан треугольника Теорема о высотах треугольника

Свойства биссектрисы неразвёрнутого угла Теорема. Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. (с.173,п.74) Доказать: МЕ = МК Теорема ( обратная).Точка, лежащая внутри неразвёрнутого угла и равноудалённая от его сторон, лежит на биссектрисе этого угла. (с.173,п.74) Следствие1 :геометрическим местом точек плоскости, лежащих внутри неразвёрнутого угла и равноудалённых от сторон угла, является биссектриса этого угла (с.173,п.74)

Первая замечательная точка треугольника Следствие 2. Биссектрисы треугольника пересекаются в одной точке.(с.174,п.74) Доказательство: Проведём перпендикуляры к сторонам треугольника Значит, О – точка пересечения трёх биссектрис треугольника.

Свойства серединного перпендикуляра к отрезку Теорема. Каждая точка серединного перпендикуляра к отрезку равноудалена от его концов.(с.174-175,п.75) Дано: АВ – отрезок, РК – серединный перпендикуляр, М є РК Доказать: МА = МВ Теорема (обратная). Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему. (с.175,п.75) Следствие1:геометрическим местом точек плоскости, равноудалённых от концов отрезка, является серединный перпендикуляр к этому отрезку (с.175,п.75)

Вторая замечательная точка треугольника Следствие 2. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.(с.174,п.75) Доказать: р – серединный перпендикуляр к ВС, О є р Доказательство: n – серединный перпендикуляр к АС и О є n, значит, ОА = ОС. k – серединный перпендикуляр к АВ и О є k, значит, ОА = ОВ. Следовательно, ОА = ОВ =ОС, значит, О лежит на серединном перпендикуляре к стороне ВС, т. е. на р. Значит, О – точка пересечения серединных перпендикуляров k, n, p.

Вторая замечательная точка треугольника (продолжение) Ещё возможное расположение:

Третья замечательная точка треугольника Свойство. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2: 1, считая от вершины. (центр тяжести треугольника – центроид) Доказательство проведено ранее: задача 1 п. 64.с.146

Четвёртая замечательная точка треугольника Теорема. Высоты треугольника или их продолжения пересекаются в одной точке(ортоцентр).(с.176,п.76)

Доказательство: Получим: АСВЕ – параллелограмм, значит, АС = ВЕ АСТВ – параллелограмм, значит, АС = ВТ Следовательно, ВЕ = ВТ, т. е. В – середина ЕТ. Получим: ВН – серединный перпендикуляр к ЕТ. Аналогично, СМ – серединный перпендикуляр к ТУ и АК — серединный перпендикуляр к УЕ.

Замечательные точки треугольника.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс добавлен 13.01.2022
Сейчас обучается 944 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Курс добавлен 13.01.2022
Сейчас обучается 704 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс добавлен 13.01.2022
Сейчас обучается 338 человек из 72 регионов

Ищем педагогов в команду «Инфоурок»

Приходько Светлана НиколаевнаНаписать 241 26.05.2020

Номер материала: ДБ-1179724

25.05.2020 0

24.05.2020 0

23.05.2020 0

02.05.2019 461

01.05.2019 450

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Стартовал региональный этап Всероссийской олимпиады школьников

Время чтения: 2 минуты

Более половины россиян сталкиваются с конфликтами в родительских чатах

Время чтения: 2 минуты

Детский омбудсмен предложила ужесточить наказание за преступления против детей

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Утвержден список федеральных инновационных площадок в образовании на 2022 год

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Математика это не ИсламСкачать

Четыре замечательные точки треугольника

Вы будете перенаправлены на Автор24

В треугольнике есть так называемые четыре замечательные точки: точка пересечения медиан. Точка пересечения биссектрис, точка пересечения высот и точка пересечения серединных перпендикуляров. Рассмотрим каждую из них.

Видео:ГЕОМЕТРИЯ 8 класс: 4 замечательные точкиСкачать

Точка пересечения медиан треугольника

О пересечении медиан треуголника: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.

Доказательство.

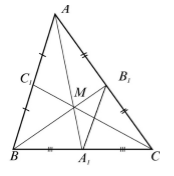
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 1).

Рисунок 1. Медианы треугольника

По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $angle ABB_1=angle BB_1A_1, angle BAA_1=angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда

Аналогично доказывается, что

Видео:Четыре точки на окружности | ЕГЭ-2017. Задание 16. Математика. Профильный уровень| Борис ТрушинСкачать

Точка пересечения биссектрис треугольника

О пересечении биссектрис треугольника: Биссектрисы треугольника пересекаются в одной точке.

Доказательство.

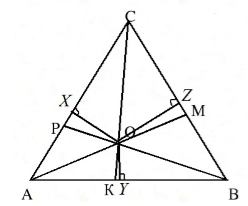
Рассмотрим треугольник $ABC$, где $AM, BP, CK$ его биссектрисы. Пусть точка $O$ — точка пересечения биссектрис $AM и BP$. Проведем из этой точки перпендикуляры к сторонам треугольника (рис. 2).

Рисунок 2. Биссектрисы треугольника

Готовые работы на аналогичную тему

Для доказательства нам потребуется следующая теорема.

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

По теореме 3, имеем: $OX=OZ, OX=OY$. Следовательно, $OY=OZ$. Значит точка $O$ равноудалена от сторон угла $ACB$ и, значит, лежит на его биссектрисе $CK$.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Точка пересечения серединных перпендикуляров треугольника

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство.

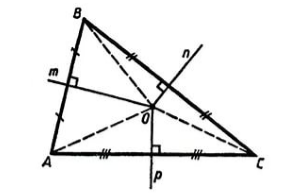
Пусть дан треугольник $ABC$, $n, m, p$ его серединные перпендикуляры. Пусть точка $O$ — точка пересечения серединных перпендикуляров $n и m$ (рис. 3).

Рисунок 3. Серединные перпендикуляры треугольника

Для доказательства нам потребуется следующая теорема.

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов данного отрезка.

По теореме 3, имеем: $OB=OC, OB=OA$. Следовательно, $OA=OC$. Значит точка $O$ равноудалена от концов отрезка $AC$ и, значит, лежит на его серединном перпендикуляре $p$.

Видео:Первое условие принадлежности четырех точек одной окружностиСкачать

Точка пересечения высот треугольника

Высоты треугольника или их продолжения пересекаются в одной точке.

Доказательство.

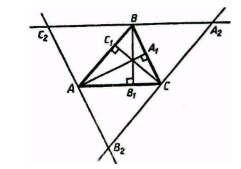
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его высоты. Проведем через каждую вершину треугольника прямую, параллельную противоположной вершине стороне. Получаем новый треугольник $A_2B_2C_2$ (рис. 4).

Рисунок 4. Высоты треугольника

Так как $AC_2BC$ и $B_2ABC$ параллелограммы с общей стороной, то $AC_2=AB_2$, то есть точка $A$ — середина стороны $C_2B_2$. Аналогично, получаем, что точка $B$ — середина стороны $C_2A_2$, а точка $C$ — середина стороны $A_2B_2$. Из построения мы имеем, что $_1bot A_2B_2, _1bot A_2C_2, _1bot C_2B_2$. Следовательно, $_1, _1, _1$ — серединные перпендикуляры треугольника $A_2B_2C_2$. Тогда, по теореме 4, имеем, что высоты $_1, _1, _1$ пересекаются в одной точке.

Видео:Четыре замечательные точки треугольникаСкачать

Пример задачи на использование 4 замечательных точек треугольника

Серединные перпендикуляры к сторонам $AB$ и $AC$ треугольника $ABC$ пересекаются в точке $D$ стороны $BC$. Докажите, что

а) точка $D$ — середина стороны $BC$.

б) $angle A=angle B+angle C$

Решение.

а) По теореме 4, все серединные перпендикуляры пересекаются в точке $D$. Следовательно, $D$ — основание серединного перпендикуляра к стороне $BC$. Значит точка $D$ — середина стороны $BC$.

б) Так как $X$ и $D$ — середины сторон, то $XD$ — средняя линия треугольника. Тогда, по теореме о средней линии треугольника $XD||AC$. Значит,$angle A=angle DXB$, как соответственные углы. Значит, $angle A=^0$. Тогда$angle B+angle C=^0-angle A=^0-^0=^0=angle A$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 29 03 2022