Касательная окружность 8 класс задачи

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Решение задач по теме: «Касательная к окружности».
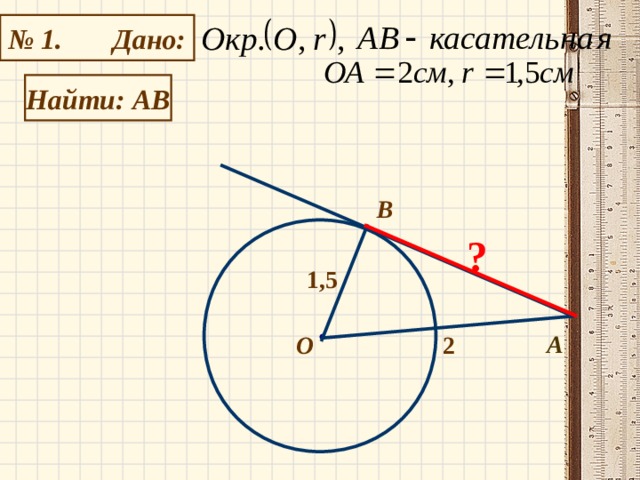
учебно-методическое пособие по алгебре (8 класс)

Подборка задач по теме на применение понятия касательной к окружности и ее свойст при решении задач, сдесь же задачи для домашней работы на отработку материала урока.

Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Скачать:

Видео:КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ в точке ЗАДАЧИ 8 классСкачать

Предварительный просмотр:

Касательная к окружности.

1. Прямая AB касается окружности с центром O радиуса 5 см. Известно, что AO=OB=13 см. Чему равна длина AB?
2. Стороны AB, BC и AC треугольника ABC касаются окружности с центром O в точках M, K и P соответственно так, что BM=5 см, PC=7 см, а периметр треугольника ABC равен 32 см. Найдите длину стороны AC.
3. AB и BC- отрезки касательных, проведенных к окружности с центром O радиуса 6 см. Найдите периметр четырехугольника ABCO, если ∠ ABC=60º.
4. Угол между диаметром AB и хордой AC равен 30º. Через точку C проведена касательная, пересекающая прямую AB в точке E. Найдите CE, если радиус окружности равен 6 см.

1. AB и BC-отрезки касательных, проведенных из точки B к окружности с центром O. OB=10, AO=5. Чему равен ∠ AOC?
2. AB и BC-отрезки касательных, проведенных к окружности с центром О радиуса 10 см. Найдите периметр четырехугольника ABCO, если ∠ AOC120º.

Видео:Геометрия 8 класс: Решение задач на касательную к окружностиСкачать

По теме: методические разработки, презентации и конспекты

Задачи по теме касательная к окружности

Задачи для подготовки к ЕГЭ.

Презентация «Задачи по теме Касательная к окружности»

Презентация содержит подборку задач на отработку навыка решения задач по теме «Касательная к окружности».

Решение задач по теме: «Движение по окружности» Подготовка к ЕГЭ задание «В»

Решение задач по теме «Движение по окружности».

Решение задач по теме «Касательная к окружности»

Разбор задач с помощью готовых рисунков.

Решение задач практической направленности по теме «Окружность» (геометрия 8 класс)

Сценарный план урока геометрии для 8 класса. (по теме «Окружность»).

Решение задач по теме «Касательная к окружности».

Данная разработка урока систематизирует знания учащихся по теме «Касательная к окружности&quot.

Видео:ОГЭ за одну минуту | ОГЭ, математика, задание 16 (окружность и касательная)Скачать

Касательная к окружности. Решение задач

Просмотр содержимого документа
«Касательная к окружности. Решение задач»

8 класс. Геометрия

Решение задач по теме «Касательная к окружности»

Учитель математики: Барсукова И.Е.

Повторение теоретического материала

Как вы думаете, сколько общих точек могут иметь прямая и окружность?

r две общие точки одна общая точка не имеют общих точек Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку . Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки . Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек . » width=»640″

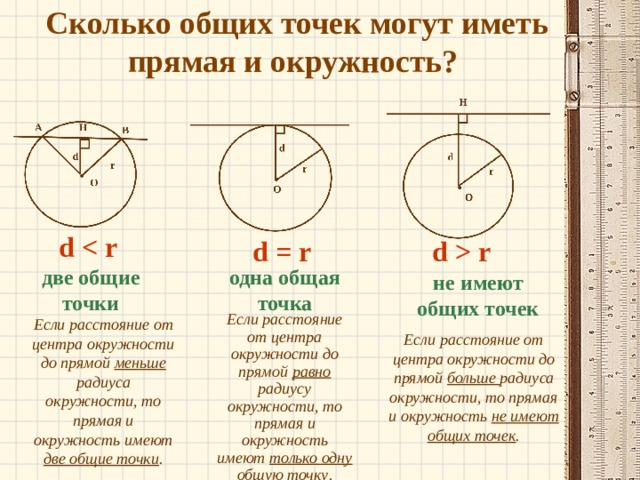
Сколько общих точек могут иметь прямая и окружность?

две общие точки

одна общая точка

не имеют общих точек

Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку .

Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки .

Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек .

Касательная к окружности

Определение: П рямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

m – касательная к окружности с центром О

М – точка касания

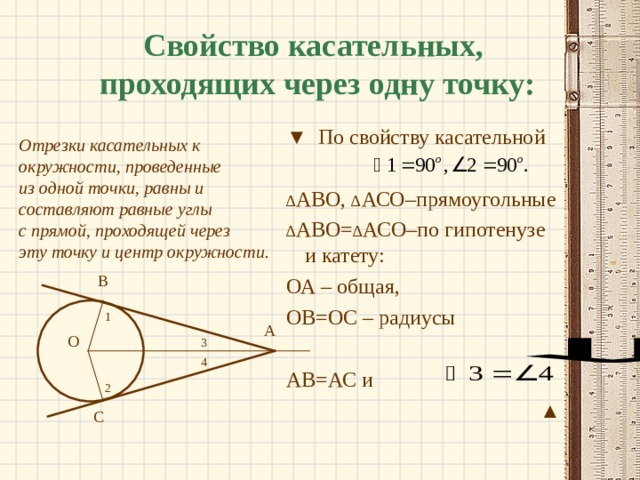
Свойство касательных, проходящих через одну точку:

Отрезки касательных к

из одной точки, равны и

составляют равные углы

с прямой, проходящей через

эту точку и центр окружности.

▼ По свойству касательной

∆ АВО= ∆ АСО–по гипотенузе и катету:

Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна радиусу, то она является к асательной.

окружность с центром О

m – прямая, которая проходит через точку М

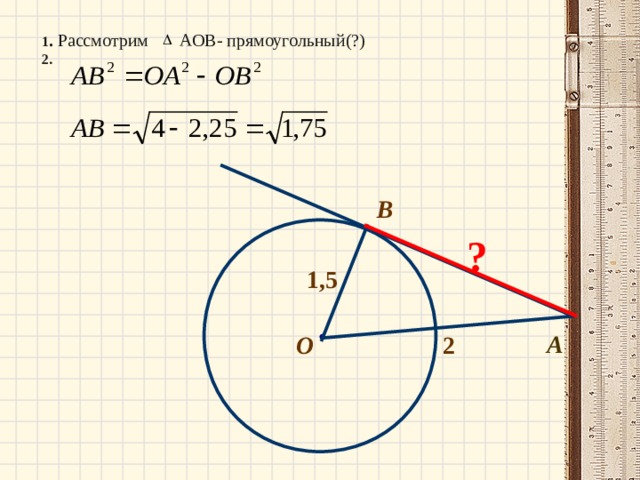
1 . Рассмотрим АОВ- прямоугольный(?)

Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Касательная к окружности

О чем эта статья:

Видео:Урок по теме КАСАТЕЛЬНАЯ К ОКРУЖНОСТИСкачать

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

🔥 Видео

КАСАТЕЛЬНАЯ к ОКРУЖНОСТИ 8 класс геометрия АтанасянСкачать

Геометрия. 8 класс. Урок 9 "Касательные к окружности"Скачать

8 класс геометрия Касательная к окружности Решение задачСкачать

Решение задач Касательная к окружностиСкачать

Геометрия 8 класс : Касательная к окружностиСкачать

71. Касательная к окружностиСкачать

Касательные к окружности пересекаются в точке. Теорема и решение задач. Геометрия 7-8 классСкачать

Касательная к окружности | Геометрия 7-9 класс #69 | ИнфоурокСкачать

Касательная к окружности. Видеоурок 18. Геометрия 8 классСкачать

Касательные к окружности | Задачи 11-20 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать

Геометрия 8 класс. Касательная к окружностиСкачать

Геометрия 8 класс Урок 9 Касательные к окружностиСкачать