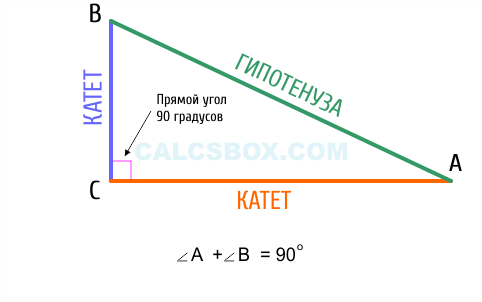
Какой треугольник называется прямоугольником элементы (5 видео)

Прямоугольный треугольник

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами .

Содержание

Плоские геометрические фигуры: свойства и основные формулы
Четырёхугольник
Основные свойства:
Квадрат
Основные формулы:
Свойства:
Прямоугольник
Основные формулы:
Свойства:
Параллелограмм
Определения:
Основные формулы:
Свойства:
Ромб
Основные формулы:
Свойства:
Трапеция
Определения:
Основные формулы:
Свойства:
Треугольник
Определения:
Основные формулы:
Свойства:
Окружность
Определения:
Основные формулы:
Прямоугольный треугольник
Свойства и особенности прямоугольных треугольников
🔥 Видео

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Плоские геометрические фигуры: свойства и основные формулы

В статье описываются геометрические фигуры: определение, основные свойства и формулы.

Плоские геометрические фигуры:

Четырехугольник (общее для всех четырехугольников)

Квадрат

Прямоугольник

Параллелограмм

Трапеция

Треугольник

Окружность

Геометрические фигуры — это любое сочетание точек, линий и поверхностей. Геометрические фигуры разделяются на плоские и объемные.

Плоские геометрические фигуры — это фигуры, все точки которых лежат на одной плоскости. Объемные геометрические фигуры — это фигуры, не все точки которых лежат на одной плоскости.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Четырёхугольник

Четырёхугольник – это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Основные свойства:

Сумма углов четырёхугольника равна 360°
Не существует четырёхугольников, у которых все углы острые или все углы тупые.
Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.

В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Квадрат

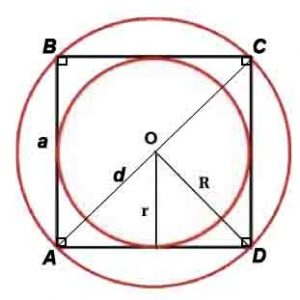
Квадрат – правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Основные формулы:

Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a 2 или S=d 2 /2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2

где a-сторона, d-диагональ, P-периметр, S-площадь
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.

Свойства:

Все стороны равны, все углы равны и составляют 90°;
Диагонали квадрата равны и перпендикулярны;
У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
Квадрат является одновременно частным случаем ромба и прямоугольника.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Прямоугольник

Прямоугольник – четырехугольник, у которого все углы прямые.

Основные формулы:

Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S = d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a 2 +b 2 )/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a 2 +b 2 )/2 (теорема Пифагора)

где a, b – длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
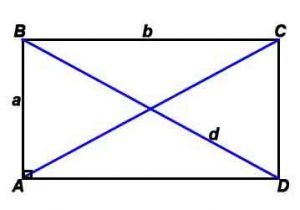
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a 2 +b 2 ) – корень квадратный из (a 2 +b 2 ).

Свойства:

Диагонали прямоугольника равны и делятся точкой пересечения пополам.
Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.

Видео:Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?Скачать

Параллелограмм

Параллелограмм – четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Определения:

Высота параллелограмма – это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.

Основные формулы:

Стороны и диагональ связаны соотношением: (d₁) 2 +(d₂) 2 =(a 2 +b 2 )*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте: S = a*h
S (Площадь) по двум сторонам и углу между ними: S=a*b*sin α
S (Площадь) по двум диагоналям и углу между ними: S=(d₁*d₂)/2*sin γ

где a, b – длины сторон, d₁, d₂ –диагонали, P-периметр, S-площадь,
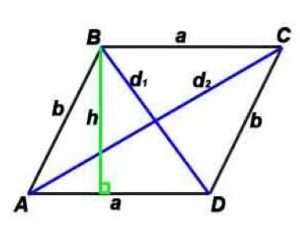
h-высота, проведенная к противоположной стороне
α – угол между сторонами параллелограмма,
γ – угол между диагоналями параллелограмма (острый).

Свойства:

У параллелограмма противоположные стороны равны и противоположные углы равны.
Сумма любых двух соседних углов параллелограмма равна 180°.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Каждая диагональ делит параллелограмм на два равных треугольника.
Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Видео:Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Ромб

Ромб – это параллелограмм, у которого все стороны равны.

Основные формулы:

Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d₁*d₂)/2
Радиус окружности, вписанной в ромб: r=h/2 или r =(d₁*d₂)/4a
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a 2 · sin α

где a – длина стороны, d₁, d₂ –диагонали, P-периметр, S-площадь,
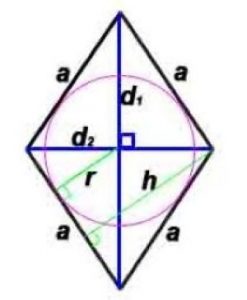
h -высота, проведенная к противоположной стороне
α – угол между сторонами ромба

Свойства:

Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d₁*d₂/4a.

Видео:Нахождение стороны прямоугольного треугольникаСкачать

Трапеция

Трапеция – четырёхугольник, у которого только две противолежащие стороны параллельны.

Определения:

Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
Средняя линия (первая средняя линия) трапеции – отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
Средняя линия (вторая средняя линия) – отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
Прямоугольная трапеция – трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.

Основные формулы:

Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2

где a,b – основания, c,d – боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d₁, d₂ –диагонали,
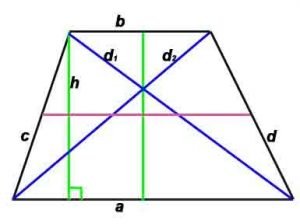
P-периметр, S-площадь, h -высота, проведенная к противоположной стороне

Свойства:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.

Видео:Геометрия. 7 класс. Урок 1 "Прямоугольный треугольник и его элементы"Скачать

Треугольник

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Определения:

Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
Высота треугольника – перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
Медиана треугольника– отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
Равнобедренный треугольник– треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
Прямоугольный треугольник – треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.

Основные формулы:

Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь: по сторонам и углу между ними: S=(a*b)/2* sin γ
по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c 2 =a 2 +b 2 (Теорема Пифагора)

где a,b, c – стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
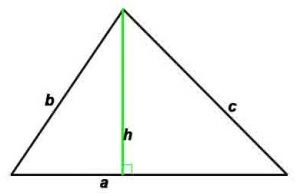
d₁, d₂ –диагонали, h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ – угол между сторонами a и b
r – радиус вписанной окружности, R – радиус описанной окружности

Свойства:

В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
Сумма углов треугольника равна 180°:
Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b| 2 =a 2 +b 2 (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.

Видео:Прямоугольник. Что такое прямоугольник?Скачать

Окружность

Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Определения:

Радиус – отрезок, который соединяет центр окружности с любой её точкой.
Хорда – отрезок, который соединяет какие-либо две точки окружности (AB).
Диаметр – хорда, проходящая через центр окружности(d). Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует.
Касательная – прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
Секущая – прямая, которая пересекает окружность в двух различных точках.

Основные формулы:

Длина окружности: L = 2πR
Площадь круга: S = π*r 2 или S = π*d 2 /4

где π = 3,14 (3,1415926535) – величина постоянная,
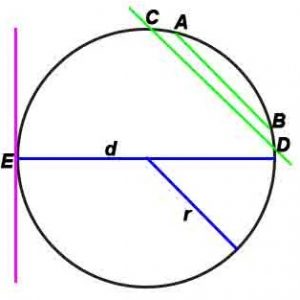
где r-радиус, d –диаметр, L – длина окружности, S-площадь.

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Прямоугольный треугольник

Треугольник в геометрии представляет одну из основных фигур. Из предыдущих уроков вы знаете, что треугольник – это многоугольная фигура, которая имеет три угла и три стороны.

Треугольник называют прямоугольным, если у него есть прямой угол, который равен 90 градусов.
Прямоугольный треугольник имеет две взаимно перпендикулярные стороны, называемые катетами; третья его сторона называется гипотенузой. Гипотенуза является самой большой стороной этого треугольника.

По свойствам перпендикуляра и наклонных гипотенуза длиннее каждого из катетов (но меньше их суммы).
Сумма двух острых углов прямоугольного треугольника равна прямому углу.
Две высоты прямоугольного треугольника совпадают с его катетами. Поэтому одна из четырех замечательных точек попадает в вершины прямого угла треугольника.
Центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы.
Медиана прямоугольного треугольника, проведенная из вершины прямоуго угла на гипотенузу, является радиусом описанной около этого треугольника окружности.

Видео:#Урок2 Геометрия Прямоугольный треугольник. Проекция.Тригонометрические элементы в прям.треугольникеСкачать

Свойства и особенности прямоугольных треугольников

I – е свойство. В прямоугольном треугольнике сумма его острых углов равна 90°. Против большей стороны треугольника лежит больший угол, а против большего угла лежит большая сторона. В прямоугольном треугольнике наибольшим углом, является прямоугольный угол. Если же в треугольнике самый большой угол имеет более 90°, то такой треугольник перестает быть прямоугольным, так как сумма всех углов превысить 180 градусов. Со всего этого следует, что гипотенуза является наибольшей стороной треугольника.

II – е свойство. Катет прямоугольного треугольника, который лежит против угла в 30 градусов, равен половине гипотенузе.

III – е свойство. Если же в прямоугольном треугольнике катет равняется половине гипотенузы, то и угол, который лежит напротив данного катета будет равен 30 градусам.