Какого радиуса должна быть окружность с центром в точке чтобы она касалась оси ординат?
Это задание ещё не решено, приводим решение прототипа.
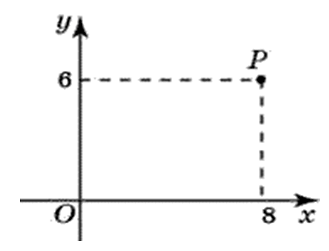
Какого радиуса должна быть окружность с центром в точке P (8; 6), чтобы она касалась оси ординат?
Для того чтобы окружность касалась оси ординат, необходимо, чтобы расстояние от ее центра — точки Р до оси ординат было равно радиусу этой окружности. Расстояние точки Р до оси ординат равно абсциссе точки Р, т. е. равно 8. Следовательно, радиус окружности должен быть равен 8.
Видео:Радиус и диаметрСкачать

Окружность с центром в начале координат
Мы уже разобрали с вами почти все типы заданий входящих в ЕГЭ связанных с координатной плоскостью, рекомендую посмотреть последнюю статью. Эта является её небольшим дополнением, принципы и подходы к решению те же. Рассмотрим задачи:
27693 (94). Какого радиуса должна быть окружность с центром в точке P (8;6), чтобы она касалась:
Окружность с центром в точке Р будет касаться оси абсцисс в точке с координатами (8;0) и её радиус будет равен шести (на эскизе изображена синим цветом).
Окружность с центром в точке Р будет касаться оси ординат в точке с координатами (0;6) и её радиус будет равен восьми (на эскизе изображена красным цветом).
27696 (97). Найдите абсциссу и ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (–2;–2), (6;–2), (6;4), (–2;4).
Как известно, точка пересечения диагоналей прямоугольника и центр описанной около него окружности совпадают. *По свойству прямоугольника его центр равноудалён от его вершин и сторон.
То есть необходимо определить абсциссу и ординату точки пересечения диагоналей прямоугольника. Сделать это можно разными способами:
1. Найти координаты середины отрезка АС (или CD) по формуле.
2. Построить прямоугольник по данным координатам на листе в клетку, вместе с его диагоналями.
Воспользуемся вторым способом:
По эскизу видно, что центр прямоугольника имеет координаты (2;1). Таким образом, абсцисса центра окружности равна двум, а ордината равна единице.
27699 (700). Найдите абсциссу и ординату центра окружности, описанной около треугольника, вершины которого имеют координаты (8;0), (0;6), (8;6).
Данный треугольник является прямоугольным. О прямоугольном треугольнике и описанной около него окружности нам известно следующее:
Гипотенуза прямоугольного треугольника и диаметр описанной около него окружности совпадают.
Подробнее об этом изложено здесь (пункт 1).
*Данное свойство рекомендую запомнить раз и навсегда, пригодится при решении многих заданий.
Так как АВ является диаметром окружности, то её центр делит этот отрезок пополам. Опытный глаз сразу «увидит», что координаты этой точки (4;3).
Если не увидели, то постройте этот треугольник на листе в клетку по данным координатам и далее вы без труда определите как расположен центр окружности. Абсцисса равна четырём, ордината равна трём.
27692. Окружность с центром в начале координат проходит через точку P (8;6). Найдите ее радиус.
27695. Найдите радиус окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (–2;–2), (6; –2), (6; 4), (–2; 4).
27698. Найдите радиус окружности, описанной около треугольника, вершины которого имеют координаты (8;0), (0;6), (8;6).
Видео:Длина окружности. Математика 6 класс.Скачать

Всё про окружность и круг
Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
📸 Видео
Радиус окружности с центром в точке O равен 85 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

№650. Радиус окружности с центром О равен 16. Найдите хорду АВ, если: a) ∠AOB = 60Скачать

Радиус Хорда ДиаметрСкачать

Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

Окружность и круг, 6 классСкачать

РАДИУС ОКРУЖНОСТЬ ДИАМЕТР КРУГ / 3 КЛАСС МАТЕМАТИКА. ЧТО ТАКОЕ ОКРУЖНОСТЬ ? ЧТО ТАКОЕ РАДИУС ?Скачать

№145. Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружностиСкачать

№147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВССкачать
На окружности с центром O отмечены точки A и B так ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Найти центр и радиус окружностиСкачать

Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

№676. Стороны угла А касаются окружности с центром О радиуса r. Найдите: а) ОА,Скачать

Окружность и круг. Центр, радиус, диаметр, хорда, дуга, сектор и длина окружности, площадь круга.Скачать

Окружность. 7 класс.Скачать

Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать

ЕГЭ 2017 | Задание 3 | Какого радиуса ... ✘ Школа ПифагораСкачать

№639. Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВСкачать
Всё про углы в окружности. Геометрия | МатематикаСкачать