Отличие правильного треугольника от равностороннего

Что такое треугольник знают дети уже в самом младшем возрасте, они умеют находить треугольник среди множества геометрических фигур. Но вот уже в школе по геометрии проходят треугольник и надо не просто узнавать треугольник, но и дать определение этому понятию.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Определение треугольника

Треугольник — это геометрическая фигура, окруженная тремя отрезками прямой (конечные точки каждых двух смежных отрезков соединены или перекрываются), называется треугольником. Точки пересечения отрезков называются вершинами треугольника, а сами отрезки между двумя соседними вершинами треугольника называются сторонами треугольника.

Посмотрите на треугольник на рисунке.

У него три вершины — , , и три стороны , и . У каждого треугольника есть имя — это имя образовано вершинами треугольника. Наш треугольник зовут ([а-бэ-цэ]). А треугольник на вот этом рисунке

будут звать ([эм-эн-ка]).

По правилам математической грамотности треугольник, как и любой другой многоугольник, следует называть, начиная с левого нижнего угла и называя все вершины по часовой стрелке.

В треугольнике можно провести особенные стороны — высоту, медиану и биссектрису. Начнем с высоты треугольника.

Видео:Формулы равностороннего треугольника #shortsСкачать

Высота треугольника

В каждом треугольнике можно провести три высоты. Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противолежащую этой вершине сторону.

Например, в треугольнике , высотой будет отрезок .

А теперь проведем из каждой вершины по высоте — получим три высоты — больше провести высот нельзя.

В этом треугольнике три высоты , , .

Про биссектрисы и медианы поговорим в других статьях. Сейчас же давайте с вами рассмотрим каким бывает треугольник.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Виды треугольника

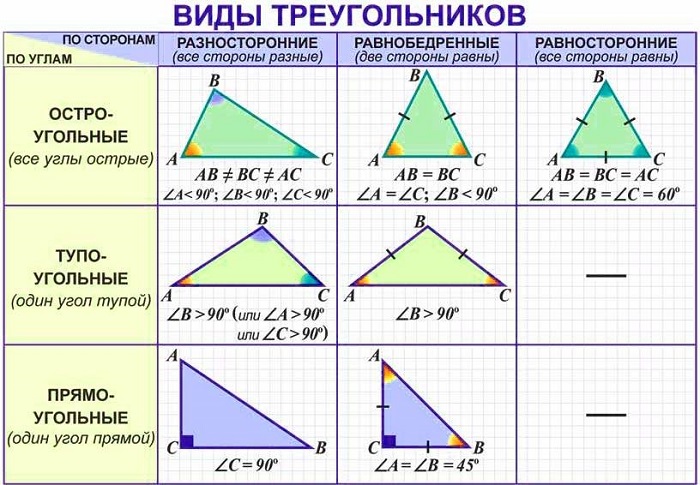
Виды треугольника могут быть по углам и по сторонам. То есть в первом случае вид треугольника зависит от того, какие в этом треугольнике углы, а во втором случае — какие в этом треугольнике стороны.

Виды треугольников по углам

В зависимости от того, все ли углы в треугольнике острые или есть тупой угол или угол, равный , треугольник бывает остроугольным, тупоугольным или прямоугольным.

Посмотрите на рисунки — перед вами три основных вида треугольника:

Виды треугольников по сторонам

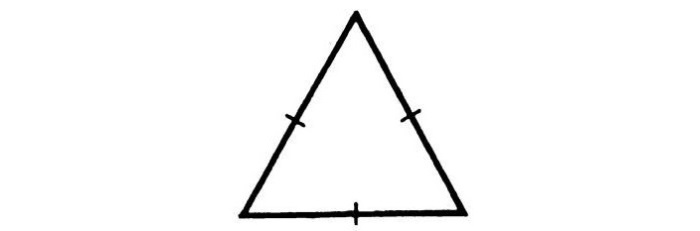
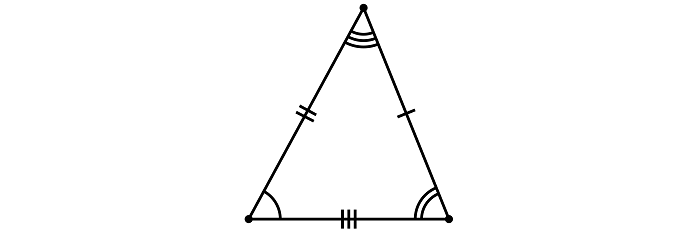
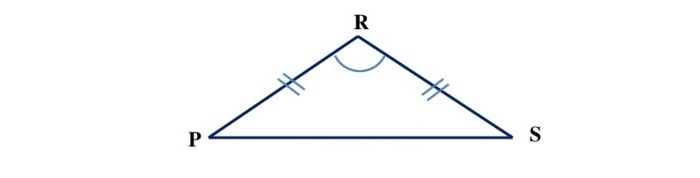
Если у треугольника все стороны равны, то такой треугольник называют равносторонним или правильным. Если у треугольника равны только две стороны, то такой треугольник называют равнобедренным.

На рисунке показаны равносторонний и равнобедренный треугольники.

Видео:НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать

Свойства сторон треугольника

Треугольник имеет важные свойства и характеристики.

Устойчивость — это важное свойство треугольника, оно вам еще пригодится в курсе физики. Но вначале мы с ним знакомимся на уроках геометрии.

Треугольник устойчив на любой своей стороне — то есть чтобы вывести его из состояния равновесия надо приложить силу.

Свойства сторон: разница между любыми двумя сторонами треугольника меньше, чем третья сторона, а также любая сторона треугольника меньше, чем сумма двух других сторон. То есть:

Например, пусть наш треугольник имеет длины двух сторон , а см. В каком диапазоне будет размер третьей стороны треугольника?

Решение: согласно свойству сторон треугольника, получим:

Таким образом, третья сторона треугольника может быть в диапазоне от 4 до 10 см. Или в целых числах ее длина может быть 5, 6, 7, 8 или 9 см.

Правило существования треугольника

Используя свойство сторон треугольника мы можем определить существует ли треугольник с определенными сторонами.

Для проверки сложите длины самых коротких сторон и если сумма их больше длины самой большой стороны, тогда треугольник существует.

Например, существует ли треугольник с длинами сторон 3, 7 и 15 см?

Решение: проверим по свойству сторон треугольника: складываем две самые короткие стороны 3 и 7 см: 3+7=10, а 10 7 — треугольник с такими длинами сторон существует.

Видео:Формулы равностороннего треугольника #shortsСкачать

Свойство углов в треугольнике

Сумма всех углов в треугольнике равна .

Согласно этому свойству мы всегда можем, зная два угла в треугольнике, найти его третий угол. В прямоугольном треугольнике сумма двух острых углов всегда равна .

Например, пусть известно, что в треугольнике , , , нужно найти .

Так как сумма углов в треугольнике равна , то находим:

.

Ответ: .

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Элементы композиции

Многие школьники спрашивают — а зачем нам знать про треугольник, как это может пригодиться в обычной жизни? Треугольник — простая фигура из которой можно составить более сложные. Это используется во многих сферах жизни, например, вы можете эргономично убирать в своей комнате, или красиво выкладывать бутерброды. Например, из двух равных треугольников можно составить параллелограмм.

А из двух равных прямоугольных треугольником — прямоугольник или квадрат. Два треугольника могут образовать трапецию, так как на рисунке. А вот какую фигурку можно смоделировать для программируемой игры — она вся сделана из треугольников:

Мы, рассмотрели самые важные свойства треугольника, и в дальнейшем изучим еще больше разных интересных свойств, закономерностей. Несмотря на свою простоту, треугольник таит в себе много загадок и открытий.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Свойства равностороннего треугольника: теория и пример задачи

В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Определение равностороннего треугольника

Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.

Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.

Видео:Формулы для равностороннего треугольника.Скачать

Свойства равностороннего треугольника

Свойство 1

В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.

Свойство 2

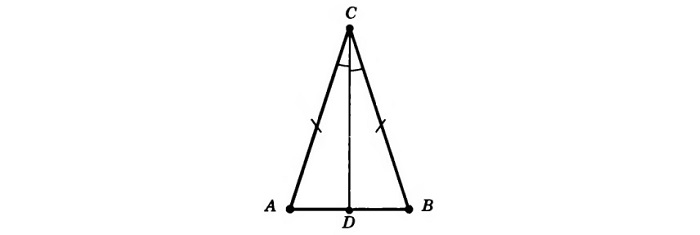
В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.

CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.

Свойство 3

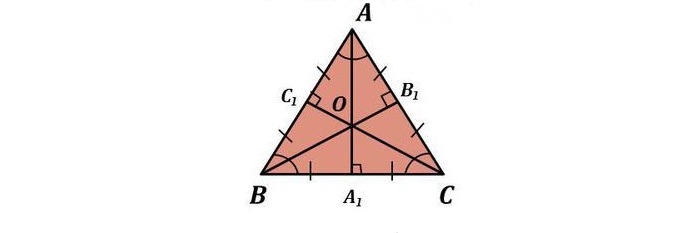
В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.

Свойство 4

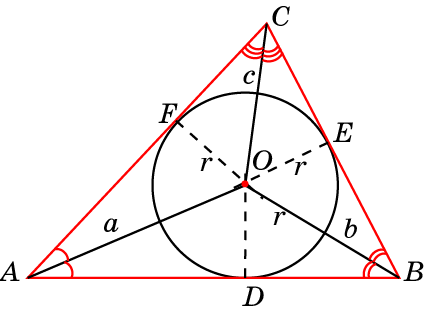
Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.

Свойство 5

Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.

• R – радиус описанной окружности;
• r – радиус вписанной окружности;
• R = 2r.

Свойство 6

В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:

1. Высоту/медиану/биссектрису:

2. Радиус вписанной окружности:

3. Радиус описанной окружности:

4. Периметр:

5. Площадь:

Видео:Геометрия - Построение правильного треугольникаСкачать

Пример задачи

Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.

Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Остроугольный треугольник — виды, свойства и признаки

Одна из центральных тем на уроках геометрии – остроугольный треугольник, составная часть своих более сложных аналогов и иных тригонометрических форм.

Азы изучения точной науки начинаются с рассмотрения уникальной комбинации из трех сторон и острых углов.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Виды, признаки и свойства остроугольных треугольников

Трехсторонние фигуры разделяются на множество подвидов и категорий.

Общая классификация по наибольшему углу делит их на 3 группы:

Они располагают как общими для формы с тремя сторонами характеристиками, так и специфическими признаками.

3 угла, сумма которых равна 180°, (величина каждого меньше 90°) и 3 стороны;

сумма длин любых двух сторон больше оставшейся третьей.

Свойства остроугольной фигуры определяются вспомогательными геометрическими линиями, всегда находящимися внутри него:

1. Биссектрисы, делящие углы пополам, являются центром, вокруг которого можно нарисовать вписанную окружность.

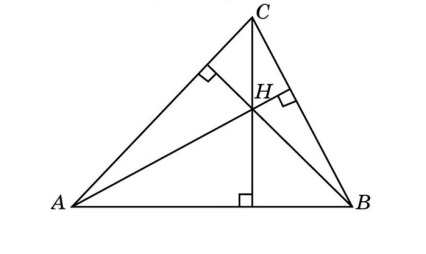
2. Высоты пересекаются в одной точке, образуя ортоцентр.

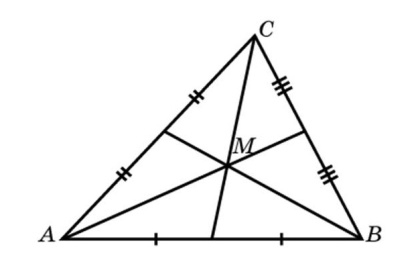
3. Медианы в точке пересечения пролегают в пропорции 2:1 (2 трети до центра и 1 треть после).

Уникальные особенности зависят от разновидностей фигуры.

Видео:Площадь равностороннего треугольникаСкачать

Равносторонний треугольник

«Идеальный» правильный треугольник, облегчающий решение задач. Определение, форма и свойства данной геометрической формы исходят из названия — все углы равны 60°, а стороны равны друг другу.

Полное равенство придает и другую особенность: медианы, биссектрисы и высоты полностью совпадают.

Видео:7 фактов про равносторонний треугольникСкачать

Разносторонний треугольник

Наиболее часто встречаемый на чертежах в геометрии вариант, один из самых трудноразрешимых видов. Разносторонними бывают и прямоугольные, и тупоугольные фигуры.

Уникальных отличий не имеет, только общие:

все параметры имеют разные значения;

совпадений между вспомогательными линиями нет.

Видео:Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

Равнобедренный остроугольный треугольник

Здесь при основании (стороне, не равной остальным) находятся равные друг другу 2 стороны и 2 угла. Выглядит как вытянутый в одну сторону равносторонний треугольник.

проведенная к основанию линия – и биссектриса, и высота, и медиана;

вспомогательные линии из крайних точек при основании совпадают.

Видео:Равносторонний треугольник в окружностиСкачать

Равнобедренный тупоугольный треугольник

Пусть он и называется равнобедренным, но из-за наличия угла более 90° не является остроугольным и является представителем другой группы.

Начертить его сложнее (рисунок следует начинать с основания и 2 острых углов и уже после создавать тупой), но процесс решения и изучения прост.

Отличие у него одно – точка пересечения двух высот, проведенных от углов при основании, выходит за периметр треугольника. Чтобы ее обозначить, необходимо нарисовать «продолжения» равнобедренных линий. Все остальные свойства совпадают.

В ключевых и фундаментальных разделах математики именно треугольник является основой для доказательства многих теорем и помощью в решении множества задач. Твердое знание его свойств откроет путь к успехам в расчетах, вычислениях, оформлении чертежей и фото в проектных работах.

🔥 Видео

Признаки равенства треугольников. 7 класс.Скачать

Геометрия Равносторонний треугольникСкачать

№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать