Какое утверждение неверно 2 прямые называются параллельными если они не имеют общих точек

Математика | 10 — 11 классы

Сформулируйте какое либо утверждение о двух прямых, не имеющих общих точек, которое верно в пространстве, но неверно на плоскости.

Двепрямые в пространстве могут быть не параллельны и не пересекаться.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Помогите пожалуйста?

Надо ответить верно или не верно 1) Если прямые не пересекаются, то они параллельны?

2) Если две плоскости не параллельны, то они пересекаются?

3) Две прямые прямые называются перпендикулярными, если угол между ними равен 90 градусов?

4) Две плоскости не имеющие общих точек параллельны?

5) Две прямые скрещиваются, если они имеют общую точку?

6) Две плоскости называются перпендикулярными, если они пересекаются под углом 90 градусов?

7) Две прямые называются параллельными, если они не скрещиваются 8) Две плоскости называются параллельными, если они не пересекаются 9) Две прямые называются скрещивающимися, если он не параллельны 10) Две плоскости не имеющие общих точек 11) Две прямые называются параллельными, если они не имеют общих точек 12) Две плоскости называются параллельными, если угол между ними не равен 90 градусов 13) Две прямые называются скрещивающимися, если угол между ними равен 90 градусов 14) Две плоскости совпадают, если они имеют общую точку.

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

В одной книге было написано 100 следующих утверждений?

В одной книге было написано 100 следующих утверждений.

» в этой книге ровно одно неверное утверждение».

«в этой книге ровно два неверных утверждения».

. «в это книге ровно сто неверных утверждений».

Какое из этих утверждений верное?

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Какое из следующих утверждений неверно?

Какое из следующих утверждений неверно?

А)Если прямая перпендикулярна к двум прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости?

Б)если прямая перпендикулярна к плоскости, то она её пересекает?

В)если две плоскости перпендикулярны к прямой, то они параллельны?

Г) если две прямые перпендикулярны к плоскости, то они параллельны?

Видео:ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. §13 геометрия 7 классСкачать

Даны 2 равных круга , не имеющих общие точки ?

Даны 2 равных круга , не имеющих общие точки .

Мколько существует точек плоскости таких , что любая прямая проходящая через эти точки и пересикающая один круг , пересикает и другой ?

Видео:Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Какое из следующих утверждений неверно?

Какое из следующих утверждений неверно?

А)Если прямая перпендикулярна к двум прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости?

Б)если прямая перпендикулярна к плоскости, то она её пересекает?

В)если две плоскости перпендикулярны к прямой, то они параллельны?

Г) если две прямые перпендикулярны к плоскости, то они параллельны?

Видео:Параллельность прямых. 10 класс.Скачать

Сколько общих точек могут иметь :а) две прямые ;б) прямая и плоскость ;в) две плоскости?

Сколько общих точек могут иметь :

б) прямая и плоскость ;

в) две плоскости?

Видео:10 класс, 10 урок, Параллельные плоскостиСкачать

Укажите верные утверждения : а)Если плоскости перпендикулярна одной из двух параллельных прямых , то она перпендикулярна ; б)Если прямая а перпендикулярна плоскости а, то любой прямой перпендикулярна ?

Укажите верные утверждения : а)Если плоскости перпендикулярна одной из двух параллельных прямых , то она перпендикулярна ; б)Если прямая а перпендикулярна плоскости а, то любой прямой перпендикулярна а, не имеет общих точек с плоскостью а ; в) Если прямая перпендикулярная плоскости то она перпендикулярна любой прямой, паралейной этой плоскости ; г) Если одна из двух поралельных прямых перпендикулярна плоскости , то и другая прямая перпендикулярна этой плоскости ; 2)Каких геометрических фигур целой стороны могут быть перпендикулярны одной плоскости ; а)у трапеции б)у пятиугольника в)у прямоугольного треугольника г)у правильного семи уголь ника ; 3)Через точки А и В преведеные прямые, перпендикулярные плоскости а и пересекающие её в точка C и D соотведтваюшие.

Отрезок АВ не пересекающие плоскости а Укажите верные утверждения А)CD = 5 Б)CD = 4 В)ABCD — трапеция Г)CDпоролельно АС.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Выберите верные утверждения?

Выберите верные утверждения.

1) Через любые три точки, не лежащие на одной прямой, проходит единственная плоскость.

2) Если две прямые в пространстве перпендикулярны, то они пересекаются.

3) Через точку и прямую всегда можно провести плоскость.

4) Если две различные прямые перпендикулярны одной плоскости, то они перпендикулярны.

Видео:Параллельные прямые. Видеоурок 2. Геометрия 10 классСкачать

На координатной прямой отмечены точки а и с ?

На координатной прямой отмечены точки а и с .

Какое из следующих утверждений НЕВЕРНО?

Видео:Теорема 13.1. Две прямые, перпендикулярные третьей прямой, параллельны || Геометрия 7 класс ||Скачать

Что можно сказать о взаимном положении двух плоскостей, имеющих три общие точки, не лежащие на одной прямой?

Что можно сказать о взаимном положении двух плоскостей, имеющих три общие точки, не лежащие на одной прямой?

Вопрос Сформулируйте какое либо утверждение о двух прямых, не имеющих общих точек, которое верно в пространстве, но неверно на плоскости?, расположенный на этой странице сайта, относится к категории Математика и соответствует программе для 10 — 11 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

Найдем скорость сближения охотников : 80 + 70 = 150 м / мин 450 : 150 = 3 мин Через 3 мин охотники встретятся, значит собака бегала 3 минуты со скоростью 12км / ч = 1200 : 60 = 200 м / мин. 3 * 200 = 600 метров пробежала собака. Ответ : 600 метров.

1)100 : 5 = 20(см) доля 1 / 6 второго полотенца 2)20•6 = 120(см) длина второго полотенца 3)100•2 = 200(см)длина третьего полотенца.

Второе 1 м 20 см треть пол метра.

22 + 30 = 52 52–40 = 12 30–12 = 18 18·2 = 36 36 + 12 = 48 48 : 2 = 24. Ответ : 24 девочек.

160 — 160 = 0 960 : 2потом : 3 = 160 960 : 6 = 160.

555 миллионов 55 000 000 + 666 000 + 777 555 000 000 + 777 000.

5 кг карт. — 75 рублей 45 рублей — ? Кг картофеля 1)75 : 5 = 15(р. ) — цена 1 кг картофеля 2)45 : 15 = 3(кг) Ответ : 3 кг картофеля можно купить на 45 рублей.

( a + b)×(a — b) = a² — b² Насчет первого не уверена, там точно минусы.

D(диагональ) = * a(сторона квадрата) d = 6 * 2 = 12.

Диагональ квадрата равна корень2 * сторону квадрата, то есть : d = корень2 * а = корень2 * 6корень2 = 6 * 2 = 12 Ответ : 12.

Видео:Параллельность прямых. Практическая часть. 10 класс.Скачать

Параллельные прямые. Признаки параллельности прямых

Как мы знаем, прямые либо пересекаются (т.е. имеют одну общую точку), либо не пересекаются (т.е. не имеют ни одной общей точки).

Определение 1. Две прямые на плоскости называются параллельными , если они не пересекаются.

Если прямые a и b параллельны, то это обозначают так:

.

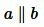На рисунке Рис.1 изображены прямые a и b, которые перпендикулярны к прямой c. В этом случае эти прямые не пересекаются (см. статью Перперндикулярные прямые), т.е. они параллельны (Определение 1).

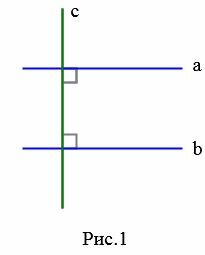Понятие параллельности можно распространять и на отрезки.

Определение 2. Два отрезка называются параллельными , если они лежат на параллельных прямых (Рис.2).

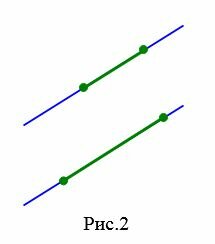Аналогично определяется параллельность отрезка и прямой, отрезка и луча, двух лучей, луча и прямой.

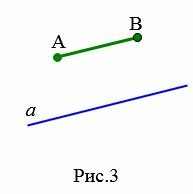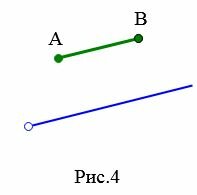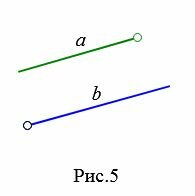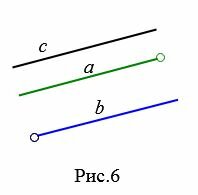На Рис.3 отрезок AB пераллелен к прямой a поскольку прямая, проходящай через отроезок AB параллельна прямой a. На рисунке Рис.4 отрезок AB пераллелен к лучу a так как прямые, проходящие через отрезок AB и луч a параллельны. Для Рис.5 и Рис.6 можно сделать аналогичные рассуждения.

Видео:10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Признаки параллельности прямых

Определение 3. Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

При пересечении прямой c с a и b образуются восемь углов, некоторые пары из которых имеют специальные названия (Рис.7):

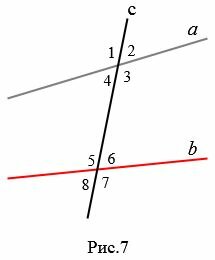• накрест лежащие углы: 3 и 5, 4 и 6;
• односторонние углы: 4 и 5, 3 и 6;
• соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.

Определим признаки параллельности двух прямых, связанные с этими парамы углов.

Теорема 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Доказательство. Предположим, что при пересечении прямых a и b секущей AB накрест лежащие углы равны: (Рис.8).

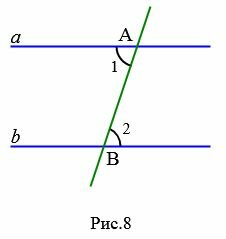Докажем, что .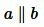

Если углы 1 и 2 прямые (Рис.9), то получается, что прямые a и b перпендикулярны прямой AB и, следовательно, они параллельны (теорема 1 статьи Перперндикулярные прямые и определение 1 настоящей статьи).

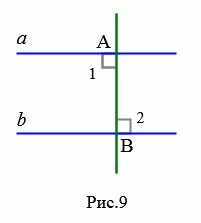Предположим, что углы 1 и 2 не прямые (Рис.10).

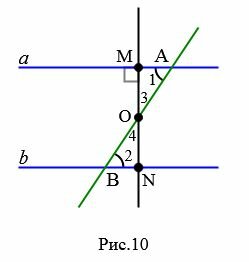Найдем середину отрезка AB и обозначим через O. Из точки O проведем перпендикуляр OM к прямой a. На прямой b отложим отрезок BN равной отрезку MA. Треугольники OAM и OBN равны по двум сторонам и углу между ними, так как OA=OB, MA=NB, . Тогда и .

означает, что точка N лежит на продолжении луча MO, т.е. точки M, O, N лежат на одной прямой. Угол BNO прямой (поскольку угол AMO прямой). Получается, что прямые a и b перпендикулярны к прямой MN, следовательно они параллельны.

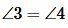
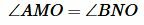
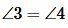
Теорема 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Доказательство. Пусть при пересечении прямых a и b секущей с соответственные углы равны, например (Рис.11).

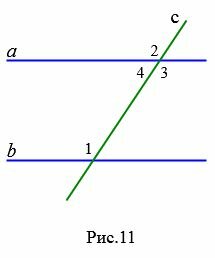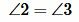
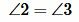
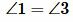
Так как углы 2 и 3 вертикальные, то . Тогда из и следует, что . Но углы 1 и 3 накрест лежащие и, по теореме 1, прямые a и b параллельны.

Теорема 3. Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

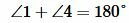
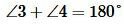
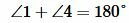
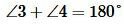
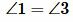
Доказательство. Пусть при пересечении прямых a и b секущей с сумма односторонних углов равна 180°, например (Рис.11). Из рисунка видно, что углы 4 и 3 смежные, т.е. . Из и следует, что . Но углы 1 и 3 накрест лежащие и, по теореме 1 прямые a и b параллельны.

Видео:Ответы на вопросы к главе 1 - Геометрия 10-11 класс АтанасянСкачать

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №4. Параллельность прямых, прямой и плоскости

Перечень вопросов, рассматриваемых в теме

1. Определение параллельных прямых;
2. Теорема о единственности прямой, параллельной данной, проходящей через данную точку;
3. лемма о двух параллельных прямых;
4. теорему о параллельности трех прямых;
5. определение параллельных прямой и плоскости;
6. признаком параллельности прямой и плоскости.

Глоссарий по теме

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Определение. Скрещивающиеся прямые − прямые, которые не лежат в одной плоскости.

Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 10-11 кл.– М.: Просвещение, 2014. 255 с.

Зив Б. Г. Дидактические материалы. Геометрия 10 кл. – М.: Просвещение, 2014. 96 с.

Глазков Ю. А., Юдина И. И., Бутузов В.Ф. Рабочая тетрадь. Геометрия 10 кл.-М.: Просвещение, 2013. 65 с.

Теоретический материал для самостоятельного изучения

Геометрия, которую мы изучаем, называется евклидовой, по имени древнегреческого ученого Евклида (3 век до нашей эры), который создал целый труд по математике под названием «Начала». В данной книге есть раздел о параллельных прямых.

В советском энциклопедическом словаре слово «параллельность» переводится с греческого языка, как «идущий рядом».

В средние века параллельность обозначалась знаком «=». В 1557 году Р. Рекордом для обозначения равенства был введен знак «=», которым мы пользуемся сейчас, а параллельность стали обозначать «║».

В книге «Начала» определение параллельных прямых звучало так «прямые, лежащие в одной плоскости и будучи бесконечно продолжены в обе стороны, ни с той, ни с другой стороны не пересекаются». Это определение почти не отличается от современного.

В области параллельных прямых работало очень много учёных: Н.И. Лобаческий (18-19 век); Аббас ал-Джаухари (работал в Багдаде в 9 веке); Фадл ал-Найризи (Богдад 10 век); Герард (Италия 12 век); Иоганн Генрих Ламберт (Берлин) и многие другие.

Каково расположение 2-х прямых на плоскости (совпадают, пересекаются, параллельны) (рис. 1 а, б, в).

Перейдем к взаимному расположению 2-х прямых в пространстве. Как и в планиметрии, две различные прямые в пространстве либо пересекаются в одной точке, либо не пересекаются (не имеют общих точек). Но второй случай допускает две возможности: прямые лежат в одной плоскости (параллельны) или прямые не лежат в одной плоскости. В первом случае они параллельны, а во втором — такие прямые называются скрещивающимися.

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Проиллюстрировать данные определения наглядно нам поможет куб.

Давайте укажем некоторые пары параллельных прямых:

AB||A₁B₁; AB|| CD; A₁B₁||C₁D₁; CD||C₁D₁; AD||A₁D₁; BC||B₁D₁; AD||BC; A₁D₁||B₁C₁.

А теперь рассмотрим некоторые пары скрещивающихся прямых, как мы отметили, они не должны лежать в одной плоскости:

AB A₁D₁; AB B₁C₁; CD A₁D₁; CD B₁C₁; BC C₁D₁; BC A₁B₁; AB B₁C₁; AB A₁D₁.

Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

1. М и а задают плоскость α
2. Прямая, проходящая через точку М параллельно прямой а, должна лежать в одной плоскости с точкой М и прямой а, т.е. в плоскости α.
3. В плоскости α через точку М проходит прямая, параллельная прямой а, и притом только одна- это нам известно из кураса планиметрии.
4. На чертеже эта прямая обозначена буквой b .
5. Следовательно, b-единственная прямая, проходящая через точку М паралельно прямой а.

Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.

Аналогично определяется праралельность отрезка и прямой, а так же паралельность двух лучей.

Лемма. Если одна из двух паралельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

1. Рассмотрим две параллельные прямые a и b и допустим, что прямая b пересекает плоскость α в точке M(а рис.).
2. Мы знаем, что через параллельные прямые a и b можно провести только одну плоскость β. (теорема)

1. Так как точка M находится на прямой b, то M также принадлежит плоскости β (б рис.). Если у плоскостей α и β есть общая точка M, то у этих плоскостей есть общая прямая p, которая является прямой пересечения этих плоскостей (4 аксиома).

1. Прямые a, b и c находятся в плоскости β.

Если в этой плоскости одна из параллельных прямых b пересекает прямую p, то вторая прямая a тоже пересекает p.

1. Точку пересечения прямых a и p обозначим за N.

Так как точка N находится на прямой p, то N находится в плоскости α и является единственной общей точкой прямой a и плоскости α.

1. Значит, прямая a пересекает плоскость α в точке N.

Нам известно из курса планиметрии, что если три прямые лежат в одной плоскости и две из них параллельны третьей, то эти две прямые параллельны. Похожее утверждение имеет место и для трех прямых в пространстве.

Теорема. Если две прямые параллельны третьей прямой, то они параллельны.

Доказательство:

Выберем точку M на прямой b.

Через точку M и прямую a, которая не содержит эту точку, можно провести только одну плоскость α (Через прямую и не лежащую на ней точку можно провести только одну плоскость).

Возможны два случая:

1) прямая b пересекает плоскость α или 2) прямая b находится в плоскости α.

Пусть прямая b пересекает плоскость α.

Значит, прямая c, которая параллельна прямой b, тоже пересекает плоскость α. Так как a∥c, то получается, что a тоже пересекает эту плоскость. Но прямая a не может одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно, предположение, что прямая b пересекает плоскость α, является неверным. Значит, прямая b находится в плоскости α.

Теперь нужно доказать, что прямые a и b параллельны.

Пусть у прямых a и b есть общая точка L.

Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек.

Так как прямые a и b находятся в одной плоскости α и у них нет общих точек, то они параллельны.

Если две точки прямой лежат в данной плоскости, то по аксиоме А₂ вся прямая лежит в этой плоскости. Из этого следует, что возможны три расположения прямой и плоскости:

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Наглядный пример, который дает представление о прямой, параллельной плоскости- это линия пересечения стены и потолка-она параллельна плоскости пола.

Теорема (Признак параллельности прямой и плоскости)
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.

Доказательство:
Доказательство проведем от противного. Пусть a не параллельна плоскости α, тогда прямая a пересекает плоскость в некоторой точке A. Причем A не находится на b, так как a∥b. Согласно признаку скрещивающихся прямых, прямые a и b скрещивающиеся.

Мы пришли к противоречию. Так как согласно данной информации a∥b, они не могут быть скрещивающимися. Значит, прямая a должна быть параллельна плоскости α.

Существует еще два утверждения, которые используются при решении задач:

1. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
2. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо тоже параллельна данной плоскости, либо лежит в этой плоскости.

Примеры и разбор решения заданий тренировочного модуля

Тип задания: Ввод с клавиатуры пропущенных элементов в тексте

Дано: в ∆ АВС КМ − средняя линия, КМ=5; ACFE- параллелограмм.

Решение: Т.к. КМ − средняя линия, то АС= 2·КМ, то АС=2·7=10

Т.к. ACFE − параллелограмм, то АС=EF=10

Тип задания: Единичный / множественный выбор

Точка М не лежит в плоскости ромба ABCD. На отрезке АМ выбрана точка Е так, что MЕ:ЕА=1:3. Точка F – точка пересечения прямой МВ с плоскостью CDE. Найдите АВ, если AD= 8 cм.

MC

Т.к. AD||BC||FK, следовательно, треугольники MFK и MBC- подобны (по трем углам). Значит

. BC=AD= 8 см;

🎥 Видео

Параллельные прямыеСкачать

Геометрия 10 класс : Параллельные плоскости и их свойстваСкачать

Взаимное расположение прямых в пространстве. 10 класс.Скачать

Параллельность прямых, плоскостей, прямой и плоскости | Математика ЕГЭ для 10 класса | УмскулСкачать

10 класс, 2 урок, Аксиомы стереометрииСкачать

7 класс, 12 урок, Перпендикулярные прямыеСкачать

Теоремы об углах, образованных двумя парал. прямыми и секущей | Геометрия 7-9 класс #30 | ИнфоурокСкачать