Каким способом древние строители чертили на земле отрезки и окружности

В наши дни окружность Земли можно измерить с помощью измерительной аппаратуры и спутников. Но можно и не изобретать никаких хитроумных инструментов, как это сделал Эратосфен более 2000 лет назад. Он вычислил размеры Земли, не покидая стен библиотеки, где работал.

Видео:Математика это не ИсламСкачать

Как Эратосфен измерил окружность Земли?

Эратосфен — греческий ученый, живший в египетском городе Александрии с 276 года по 196 год до нашей эры. Работал он в Александрийском мусейоне. Отчасти это был музей, отчасти научный центр того времени.

В музее был ботанический сад, виварий, астрономическая обсерватория и лаборатории. Одни ученые мужи вели научные диспуты в аудитории музея, другие трапезничали и беседовали в триклинии (то есть в столовой).

Эратосфен заведовал библиотекой мусейона, в которой хранилось около 100 тысяч книг, написанных на свитках папируса (разновидность бумаги, сделанной из волокон растения папируса). Эратосфен интересовался всем на свете. Он изучал философию, историю и естественные науки, был театральным критиком. Многие коллеги по мусейону считали его дилетантом, то есть человеком, который всем интересуется, но ничего не знает по истине глубоко.

Как Эратосфен измерил окружность Земли?

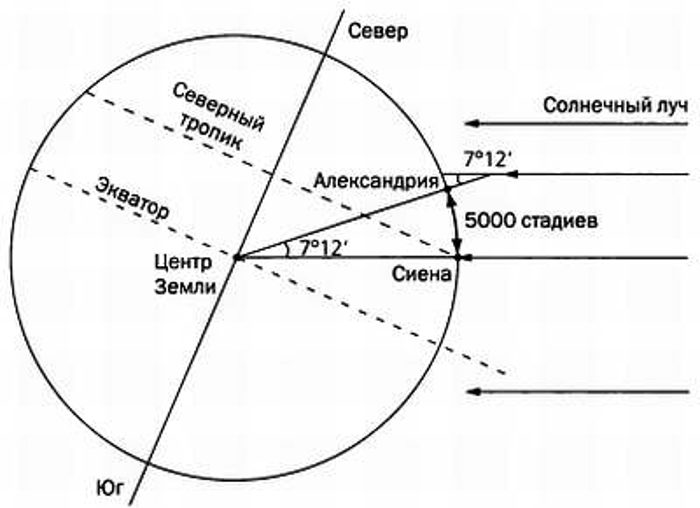
От проезжих путешественников Эратосфен услышал о необычном явлении, которое они наблюдали в Сиене, городе, расположенном далеко к югу от Александрии. Путешественники рассказали, что в полдень первого дня лета — в самый продолжительный день в году — в Сиене исчезали тени. Солнце в это время стояло прямо над головой, лучи его падали на землю отвесно вниз. Внимательно вглядываясь в воду водоема, можно было рассмотреть отражение Солнца на дне.

Эратосфен съездил в Сиену и убедился в этом сам. Вернувшись в Александрию, он обнаружил, что и в самый длительный день года в полдень стены мусейона продолжали отбрасывать тень на землю. Основываясь на этом простом наблюдении, он смог вычислить окружность Земли. Вот как он это сделал.

Видео:Как Эратосфен измерил диаметр Земли?Скачать

Вычисления окружности

Эратосфен знал, что из – за громадного расстояния от Земли до Солнца, лучи последнего достигают и Сиены и Александрии параллельными лучами. То есть лучи Солнца, падающие на землю в Александрии, параллельны лучам, падающим на землю в Сиене в то же время. Если бы Земля была плоской, то тени исчезали бы на ней повсеместно 21 июня. Но так как, рассуждал он, Земля искривлена, то в Александрии, удаленной от Сиены на 500 миль (1 миля равна 1,609 километра) к северу, местные стены и колонны наклонены по отношению к сиенским стенам и колон нам под некоторым углом.

Вычисления окружности

Итак, в полдень первого дня лета Эратосфен измерил тень, отбрасываемую обелиском, стоявшим неподалеку от мусейона. Зная высоту обелиска, он смог легко вычислить длину линии, соединяющей вершину обелиска и конец тени. Получился воображаемый треугольник. После того как треугольник был «очерчен», оставалось, используя известные к тому времени правила геометрии, вычислить его углы. И Эратосфен их вычислил. Он нашел, что угол отклонения обелиска от солнечного луча составляет чуть больше 7 градусов.

Так как в Сиене вертикальные предметы не отбрасывали тени, то угол между ними и солнечным лучом составлял ноль градусов. Короче, никакого угла не было. Это означало, что Александрия отстоит по земной окружности от Сиены на 7 градусов. Такой угол между городами — это 1 /50 часть окружности. Всякая окружность содержит 360 градусов, земная окружность в этом смысле не исключение. Эратосфен умножил расстояние между Сиеной и Александрией — 500 миль — на 50 и получил значение окружности Земли. Оно оказалось равным 25 тысячам миль. Современные ученые, измерившие с помощью высококлассной техники окружность Земли, нашли ее равной 24 894 тысяч миль. Все таки Эратосфен оказался первоклассным ученым, а не дилетантом.

Видео:Построение эвольвенты окружностиСкачать

Определение расстояний на земной поверхности

В настоящее время существует целая наука — геодезия, которая занимается определением расстояний на земной поверхности. Геодезисты используют специальные приборы для определения угловых расстояний. Они изучают колебания силы тяжести на нашей планете, чтобы выявить истинную форму Земли. Для вычисления углов используют спутники. Такой спутник перемещается в вершину воображаемого треугольника, два других его угла помещают в заданных точках на земной поверхности.

Видео:ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]Скачать

Как вычислили окружность Земли

Если Вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Видео:6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Из истории линейки, циркуля и транспортира

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Вестник Пермского Университета

2017 История Физико-математических наук Вып.

Из истории линейки, циркуля и

Пермский государственный гуманитарно-педагогический университет, Россия, 614000, Пермь, ул. Сибирская, 24

e — mail : malykh @ pspu . ru ; контакт. телефон: (342) 280-37-55

МБОУ «Гимназия №17»

Россия, 614000, Пермь, ул. Ленина, 31

e — mail : elena — bezenkova @ yandex . ru ; контакт. телефон: 8-951-943-5487

Рассмотрены классические средства, используемые для решения конструктивных задач: циркуль и линейка. Описаны их виды в процессе усовершенствования. Представлены инструменты для измерения и вычисления различных величин. Приведены исторические сведения.

Ключевые слова: классические средства ; линейка ; циркуль ; транспортир ; вычислительные, измерительные инструменты ; величины ; приложения ; исторические сведения.

Невозможно представить развитие человеческой культуры без умения выполнять геометрические построения. Зарождение первых пространственных образов относится к доисторическим временам. Возведение жилищ, проведение в них перегородок, изготовление посуды, шитье одежды и другие виды практической деятельности дали обобщенное понятие прямой линии, геометрических фигур, а также тел вращения и их частей. Постепенно формировалось учение и о геометрических построениях. В практической деятельности строителям, архитекторам, скульпторам, художникам часто приходилось делить линию на отрезки или круг на части, строить окружность или угол, выполнять замеры деталей или переносить их с рисунка на материал, то есть выполнять геометрические построения. С этой целью были созданы чертежные инструменты.

Следует заметить, что и ученые, начиная с Пифагора ( VI – V вв. до н.э.), использовали только циркуль и линейку без делений, то есть приборы, позволяющие проводить прямые линии, отрезки, окружности и их части. История циркуля и линейки насчитывает несколько тысяч лет. Ниже представлены сведения о них, ряда усовершенствованных приборов и их применении.

Люди давно научились проводить прямую линию при помощи веревки. Термин « линия », от которого возникло название «линейка», происходит от латинского linum – «льняная нить». Известно , что в древнем Египте уже использовали веревку с узелками для того чтобы наделить землю или восстановить участки после очередного разлива реки Нил. Специально обученные люди, называемые гарпетонаптами («натягиватели веревки») и занимались разметкой земли (рис. 1).

В дальнейшем уже использовались гладко обструганные дощечки–линейки. Заметим, что сначала их обстругивали с одной стороны, затем ровными стали обе, что позволило проводить параллельные линии. Впоследствии были соединены две линейки и получен наугольник. Он помогал расчертить каменную плиту при строительстве пирамид, делить на столбцы пергаментный лист. В школах Рима на дощечке прорезали окошки-буквы, и учитель водил по ним неумелой рукой ученика. В наши дни её называют трафаретом.

Не обходились без линейки и русские писцы, называя её «правильцем». В расходных книгах московских приказов XVII в. нередко встречалось название «каракса», линейка, представлявшая раму в размер листа, на которую туго натягивали нити. Положив ее на лист бумаги, писец проводил костяной палочкой линии–строчки. Вот почему рукописи того времени удивляют нас ровностью строк и четкими интервалами между ними.

Позднее линейки стали использовать также и для различного рода измерений, ставя на них метки-рисочки. Деления на линейке (сантиметры, миллиметры) появились после того, как в 1719 г. по предложению Парижской Академии наук за единицу длины был принят метр – одна десятимиллионная часть четверти Гринвичского меридиана.

Иногда для удобства с разных сторон линейки отмечали различные величины измерения, например, с одной стороны – сантиметр, а с другой – дюйм. Это английская единица измерения расстояния, равная 2,54 см. (рис. 2).

В Западной Европе эпохи Возрождения ( XVI в.) появилась потребность в сложных расчетах и вычислениях. С этой целью были изобретены логарифмы. Об этом писал Иоганн Кеплер (1571–1630) тюбингенскому профессору математики и астрономии Вильгельму Шиккарду: «. некий шотландский барон, имени которого я не запомнил, выступил с блестящим достижением: он каждую задачу на умножение и деление превратил в чистое сложение и вычитание. ». Этим шотландцем был математик Джон Непер (1550–1617), опубликовавший в Эдинбурге трактат «Описание удивительной таблицы логарифмов» (1614), в котором дал их краткое описание и свойства, а также привел семизначные таблицы логарифмов. В начале XVII в. английский астроном Эдмунд Гюнтер (1581–1626) предложил нанести на линейку логарифмическую шкалу и с помощью двух циркулей выполнять операции с логарифмами. В 20-е годы XVII в. английский математик Эдмунд Уингейт (1596–1656) усовершенствовал линейку Гюнтера, введя две дополнительные шкалы. Одновременно (1632) свой вариант линейки, мало чем отличавшейся от современного, опубликовал в трактате «Круги пропорций» Уильям Оутред (1575–1660). Он и считается автором первой логарифмической линейки. Сначала она была круговой (рис. 3), но в следующей книге «Дополнение к использованию инструмента, называемого Кругами Пропорций» (1633), ученый опубликовал описание прямоугольной логарифмической линейки (рис. 4). Таким образом, линейку стали использовать ещё и для вычислений. При нанесении на планшет координатной сетки в 1925 г. появилась еще одна линейка, которая получила название по имени её изобретателя – Фёдора Васильевича Дробышева. Впоследствии она была удлинена до 100 см и получила название «линейки Базеева-Лизунова» (ЛБЛ). В наши дни такие линейки практически не используется т.к. чертёжные работы выполняются с помощью компьютерной техники.

Объединив начертательные, измерительные и вычислительные функции этого инструмента, были созданы навигационные, артиллерийские, офицерские линейки. В медицине существует кардиологическая линейка для расшифровки электрокардиограмм.

Наблюдения за окружающим миром, вид линии раздела между небесным сводом и землей, натягивание тетивы лука и многое другое привело людей к изучению криволинейных фигур, в частности окружности. К доисторическим временам относятся первые изображения кругов. Тогда же в Вавилоне было изобретено колесо. Первые колесницы встречаются и при раскопках богатых могил конца III тысячелетия до н. э. и более позднего времени (находки в Кише, Уре и др.). Для удобства использования и повышения скорости движения колесо было усовершенствовано, что, конечно, было невозможно без циркуля, т.к. принцип его использования заключается в равном расстоянии между его концами.

Люди применяли циркуль с давних времен для изготовления ножей в форме дисков и сегментов, круглых сосудов, при строительстве храмов. Слово циркуль происходит от латинского « circulus » – «круг», «окружность», «кружок».

Согласно древнегреческой легенде, циркуль изобрел Талос, племянник легендарного архитектора, скульптора, изобретателя столярных инструментов, первого «воздухоплавательного» аппарата Дедала. В возрасте двенадцати лет он построил гончарный круг для изготовления посуды, а также пилу. Скорее всего, Талос изготовил циркуль, соединив с помощью шарнира два одинаковых по длине стержня. Дядя понял, что ученик может превзойти его в таланте и мастерстве, а потому в подходящий момент, столкнул юношу с городского вала.

В Китае также были найдены рисунки с мифическими мотивами, на которых прародители китайцев держат в руках циркуль и угольник (рис. 5).

Но мифы остаются мифами, а циркуль, наравне с линейкой, являются, пожалуй, самыми древними чертежными инструментами на земле.

Изображения окружностей на глиняных сосудах археологи обнаруживали во всех регионах мира. Изделия протогеометрической керамики можно встретить в некоторых музеях, например, в собрании Государственного музея изобразительных искусств им. А.С. Пушкина (рис. 6). Следует отметить, что не всегда эти узоры точные. Видимо, инструменты для нанесения концентрических окружностей на бока сосудов были дорогими и имелись в распоряжении не всех древних мастеров. Но в тех случаях, когда окружности построены верно, практически всегда можно заметить в их центре отметку от острия неподвижной ножки циркуля.

Заметим, что циркули с пружинной подвижной ножкой для проведения окружностей на сферической поверхности широко использовали ученые стран ислама еще с IX – X вв. На резной посуде, ювелирных украшениях, куполах и стенах храмов древних Вавилона и Ассирийского царства ( II – I вв. до н.э.) сохранились изображения очень ровных кругов. Ясно, что в этих государствах были знакомы с циркулем.

Известны три основных вида этого инструмента: веревочный циркуль, штангенциркуль и кронциркуль.

Веревочный циркуль – это веревка с отмеченными на ней (чаще всего узлами) расстояниями или с закрепленными на концах стержнями. Расстояние между соседними узлами у египтян равнялось одному фараонскому локтю, то есть не было постоянным. Известно о его применении при разметке или восстановлении земельных участков после разлива реки Нил (рис.7). Веревочный циркуль применяется и в наше время, несмотря на свою примитивность. Его используют там, где нужно нарисовать дугу окружности большого радиуса, например, при разметке спортивных арен, где использование «жесткого» циркуля неудобно. Египтянам был знаком также циркуль-землемер – это уже разновидность кронциркуля , представляющая жесткую конструкцию из трех палок, зафиксированных таким образом, что расстояние между концами двух из них постоянно. Такой землемер использовали и на Руси. Кроме этого было изобретено много других модификаций кронциркулей. Миниатюрными «балеринками» обычно пользуются для вычерчивания окружностей небольших радиусов.

Разметочный циркуль представляет два металлических стержня, соединенных пружинным

кольцом и стопорным винтом

(рис. 8). Первое обеспечивает рабочим концам циркуля возможность раздвигаться, расходиться в разные стороны, а второй необходим для фиксации расстояния между стержнями. Рабочие концы стержней делают заостренными. Применяется такой циркуль при делении линий на отрезки, построении углов, делении окружности, обозначении их дуг, а также при переносе линейных размеров с рисунка на материал.

Нутрометром (рис. 9). замеряют внутренний диаметр изделий и деталей, а кронциркулем – внешний (рис. 10).

Самый старый, дошедший до нас, уже не из мифов, а реально, железный циркуль ( I в.) нашли во Франции при раскопках древнего кургана. Множество железных и бронзовых циркулей, похожих на современные кронциркули, археологи обнаружили в пепле, засыпавшем при землетрясении в 79 г. греческий город Помпею. При раскопках в Великом Новгороде найден стальной циркуль-резец для нанесения орнаментов из мелких кружочков. Подобные узоры были широко распространены на Руси.

Штангенциркуль – это усовершенствование веревочного циркуля, применяющийся в основном в измерительной практике (рис. 11). С его помощью производят замеры внешних и внутренних размеров изделия, глубины отверстий и выступов. Точность измерения им выше, чем линейкой, т.к. цена деления его шкалы 0,1 мм. Он плотнее и надежнее соприкасается с измеряемым предметом. В музеях сохранились деревянные штангенциркули сапожников, но они давали очень грубые результаты. Позднее движущуюся планку штангенциркуля стали оснащать винтом для того чтобы передвигать её медленнее и получать более точные измерения.

Микрометр необходим в тех случаях, когда требуется особая точность определяемого размера, в первую очередь, при измерении толщины заготовок изделий или деталей (рис. 12). Цена деления микрометра 0,01 мм. Современные измерительные приборы оснащают электронными приспособлениями, что дает потрясающую точность.

«Скрещивание» кронциркуля и штангенциркуля дает компактный инструмент для вычерчивания окружностей большого радиуса. Чехословацкие инженеры на международной машиностроительной выставке в Брно получили золотую медаль за усовершенствование чертежного инструмента. При высоте циркуля 12 сантиметров можно было строить окружности диаметром до 60 сантиметров, причем довольно точно. Для этого инструмент снабжен системой удлиняющихся рычагов с винтовыми головками.

В пифагорейской гетерии существовали пропорциональные циркули. Они предназначались для пропорционального изменения в заранее заданном отношении размеров измеряемого или проектируемого объекта. Один из таких циркулей также был найден в Помпейских раскопках. Он позволял измерять расстояния, находящиеся в отношении «золотого сечения»: раствор разных концов, соединённых шарниром в средней части ножек находился в таком отношении. Нашли применение и циркули с подвижным относительно концов ножек положением шарнира (рис. 13). Они позволяли в произвольно заданной пропорции увеличивать или уменьшать размеры чертежа или измеряемого объекта. Однако его использование неудобно тем, что концы нужных отрезков отмечаются противоположными концами. Тогда он был усовершенствован тремя ножками. Расстояние между правой и левой парой ножек являлось постоянным и равным значению отношения «золотого сечения». По такому же принципу создавались циркули и с бóльшим количеством ножек.

Ученые стран ислама разрабатывали циркули и для построения конических сечений . Так, Абу Саид ал-Сиджуси ( X – XI вв.), применяя с этой целью совершенный циркуль (рис. 14), описав его в «Трактате об описании конических сечений». В зависимости от отношения величин углов α и β конец длинного стержня описывал на плоскости эллипс, ветвь гиперболы или параболу. Короткая фиксированная ножка циркуля представляла ось конуса, а длинная, свободно двигающаяся в трубке, – его образующую. Поэтому при α = β , то вычерчивалась гипербола, если α ≤ β , то – парабола, а в случае α ≥ β – эллипс.

Леонардо да Винчи (1452–1519) создал устройство, названное параболическим циркулем. Конструкция должна иметь две ножки: неподвижную или опорную, представлявшую ось конуса, и вращающуюся, составляющую с ней угол 45°. Она играла роль образующей, а точнее, её отрезка от вершины конуса до линии сечения. Первая ножка имела фиксированную длину, вторая – переменную; по сути – это трубочка, в которой свободно скользил стержень, рисуя параболу. Все устройство укреплено на треноге.

В Музее истории науки во Флоренции представлена действующая модель циркуля, изготовленная в 2001 году по эскизу Леонардо да Винчи (рис. 15). Парабола вычерчивалась на листе бумаги в наклонной плоскости, параллельной одной из «ног» треноги, причём в два шага: сначала одна часть, затем другая, начиная от вершины. Стержень соскальзывал вниз под тяжестью собственного веса и веса, прикреплённого на нитке груза.

Добавим, что конструкция совершенного циркуля аналогична той, что придумал Леонардо да Винчи, но более мобильна: она позволяла варьировать углы между осью конуса и образующей, а также между секущей плоскостью и осью конуса. Таким образом, можно всегда наклонить опорную ножку к плоскости листа под определённым углом и выбрать раствор циркуля таким образом, чтобы начертить любое коническое сечение. Однако на практике удобнее пользоваться стационарной моделью и изменять положение секущей плоскости.

Как видим, основные виды циркулей используются для снятия и перенесения линейных размеров (разметочный или делительный); вычерчивания окружностей диаметром: от 2 до 80 мм (чертежный кронциркуль); до 300 мм (чертежный или круговой); больше 300 мм (чертежный штангенциркуль); изменения масштабов снимаемого размера (пропорциональный); построения конических сечений (совершенный); парабол и эллипсов (параболический).

Циркуль всегда был незаменимым помощником архитекторов и строителей. Не случайно на фасаде одного из самых древних и красивых храмов Грузии Светицховели изображена рука мастера с циркулем.

Циркуль используется не только в черчении, навигации или картографии. Ему нашлось применение и в медицине: большой и малый толстотные циркули для измерения поперечных размеров тела человека и размеров черепа соответственно, а циркуль-калипер – для измерения толщины подкожно-жировой складки. Известен также циркуль Вебера, названный именем Эрнста Генриха Вебера (1795–1878) – немецкого психофизиолога и анатома, разработанный им для определения порога кожной чувствительности.

Кроме того, в ювелирном деле большое значение придается построению фигур с помощью циркуля, так как разметка ювелирных изделий производится тонкими царапинками, которые наносятся с помощью разметочного циркуля.

Но циркуль – не только известный всем инструмент. Этим словом названо маленькое созвездие южного полушария к западу от «Наугольника» и «Южного треугольника», рядом с α -Центавра. Кроме того, он является символом неуклонной и беспристрастной справедливости, совершенной фигурой круга с центральной точкой, источником жизни. Наряду с квадратом циркуль определяет границы отрезков прямой. В ритуальной архитектуре он символизирует знание.

У китайцев этот инструмент означает правильное поведение. Циркуль – это атрибут Фо-хи, легендарного китайского императора, считавшегося бессмертным. На картинах его сестра держит в руках квадрат, а вместе они – мужской и женский принципы, гармония инь и янь. У греков циркуль наряду с глобусом являлся символом Урании – покровительницы астрономии.

Циркуль, совмещенный с наугольником – одна из самых распространенных эмблем, символов и знаков масонов. На одной из них первый символизирует Небесный Свод, а второй – Землю.

(рис. 16). Небо в данном случае символически связано с местом, где создает план Великий Строитель Вселенной. Центральная буква «G» в одном из значений – сокращение слова «геометр», используемого в качестве одного из названий верховного существа.

Он известен с древних времён. Понятие градуса и появление первых инструментов для измерения углов связывают с развитием цивилизации в древнем Вавилоне, хотя само слово градус имеет латинское происхождение ( gradus – «шаг», «ступень»). Предполагают, что его появление было связано с созданием первого календаря. В древнем Вавилоне ученые заметили, что Солнце от восхода над горизонтом до заката проходит расстояние, равное 180 поперечникам своего диска. Они предположили, что и за ночь оно совершает такой же путь. Каждой части дали название « шаг» . И каждая последующая 60-ая часть имела свое название. Впоследствии они были переведены на латынь и стали называться «градус», « минута» и « секунда» . В истории науки эти единицы измерения сохранились в важном астрономическом труде Клавдия Птолемея (100–178) «Великие астрономические построения в XIII книгах».

История не сохранила имени ученого, изобревшего транспортир. Возможно, в древности этот инструмент называли иначе. Современное название происходит от французского « transporter », что означает «переносить». Предположительно, транспортир изобрели в древнем Вавилоне. Но там производили измерения не только им, т.к. он был неудобен для измерений на местности и решения задач прикладного характера. Именно последние являлись предметом интереса древних геометров.

Изобретение первого инструмента, позволяющего измерять углы на местности, связывают с именем древнегреческого ученого Герона Александрийского (I в.). Он описал инструмент «диоптра» (рис 17) в одноименном сочинении, который позволял измерять углы на местности и решать множество прикладных задач, описанных им в 13 книгах «Метрики». Таким образом, можно говорить о возникновении геодезии – системы наук об определении формы и размеров Земли, измерениях на земной поверхности и для отображения их на плоских планах и картах.

Транспортир состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы), разделённого на градусы от 0˚ до 180˚. В некоторых моделях – от 0˚ до 360˚.

Они изготавливаются из стали, пластмассы, дерева и других материалов. Точность его прямо пропорциональна размеру.

Известны транспортиры полукруговые (180˚) – наиболее простые и древние, круглые (360˚), геодезические . Последние бывают двух типов: для построения и измерения углов на планах и картах (рис. 18); для нанесения точек на чертежной основе по известным углам и расстояниям (рис. 19). Цена деления угломерной шкалы составляет 0,5˚, прямолинейной – 1 мм.

Имеются и более продвинутые типы транспортиров, необходимые для точных построений и измерений. К их числу относятся специальные транспортиры с прозрачной линейкой, оснащенной угломерным нониусом, которая вращается вокруг центра (рис. 20).

Насколько велико значение линейки, циркуля и транспортира в развитии цивилизации можно судить по огромному количеству рисунков, представлявших работу строителей, зодчих, художников, плотников, ювелиров, а также по приборам, представленным на картинах, изображавших великих ученых. Так, на портрете Луки Пачоли с учеником (рис.21 изображены линейка, угольник и циркуль.

История возникновения и использования таких обычных и всем доступных инструментов тесно связана с формированием наук, великими открытиями и прогрессом всего человечества.

Список литературы

Воронец А.М. Геометрия циркуля. М.: ОНТИ – ГТТИ , 1934.

Карпушина Н . Во власти сечений // В ж. «Наука и жизнь», 2012. №5. С.17–19, №6. С.15–17.

Богданов В.В., Попова С.Н. Истории обыкновенных вещей. М.: Изд-во «Педагогика-пресс», 1992.

Зверкина Г.А. О циркулях / В ж. «Живая математика». Пермь : Издат. дом Бывальцева, 2010. №5. С. 8–12.

Матвиевская Г.П. Альбрехт Дюрер – ученый. М. : Наука, 1987.

Зетаев С.И. Геометрия линейки и геометрия циркуля. М. : Изд-во АПН РСФСР, 1950.

Костовский А.Н. Геометрические построения одним циркулем. М. : Физматлит, 1984. Изд. 2.

Депман И.Я. Возникновение системы мер и способов измерения величин. М. : Учпедгиз, 1956. Вып. 1.

Планский А.Ф. Измерения и меры. М. : ГТТЛ, 1956.

Бородiн O.I. Iсторiя рoзвiтку понят i я про число i системи числен i я. Киïв : Вид. «Радяньска школа», 1978. Вид. 3.

From the history of ruler, compass and transporter

Perm State Humanitarian Pedagogical University, Russia, 614000, Perm, Sibirskaja, 24

e-mail: malykh@pspu.ru; contact phone (342) 280-37-55;

Gimnasium №17, Russia, 614000, Perm, Lenina, 31

e-mail: elena-bezenkova@yandex.ru; contact phone 8-951-943-5487.

Classical means for decision of constructive problems : compass, ruler and transporter were examined. Their different kinds in process of improvements were described. Tools for measuring and calculation of different quantities were presented. Historical information was shown.

Key words: classical means ; compass ; ruler ; transporter ; tools for measuring and calculation ; quantity ; applications ; historical information.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Для чего нужен циркуль? История его возникновения и практическое применение.

Циркуль — древнее, но до сих пор актуальное изобретение человечества. Этот предмет интересен тем, что его изобретение служило чисто научным целям. Циркуль нельзя было использоваться для охоты, как лук и стрелы, для передвижения, как колесо, для приготовления пищи и отпугивания зверей, как огонь. Только в эпоху бронзы возникла необходимость вычерчивать на земле правильные окружности. Так, с попытками начертить,измерить и обособить ту или иную окружность пришло понимание того, для чего нужен циркуль и как с ним работать.

Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Легенда о появлении циркуля

Традиция предписывает изобретение циркуля легендарному изобретателю племяннику известного Дедала – Талосу. Талос жил в Афинах. Уже в 12 лет он придумал гончарный круг, при помощи которого можно было изготавливать различную посуду. Гуляя по берегу моря, Талос поднял скелет рыбы, и это натолкнуло его на идею другого изобретения – пилы. Соединив шарниром две одинаковые палочки, Талос придумал циркуль. Дедал позавидовал гению своего племянника и однажды на прогулке столкнул Талоса с городского вала.

Видео:Строительная графика. 12 урок. Построение откосов выемок земляного сооруженияСкачать

Научная гипотеза

Есть и другая, более научная гипотеза, которая объясняет, для чего нужен циркуль, как появилась эта вещь среди предметов древних людей. Для того чтобы очертить круг, брали колышек и веревку. К веревке прикрепляли уголек или кусочек мела, и таким образом чертили окружность. Позже веревку заменили тонкой веточкой или дощечкой. Это позволило очерчивать окружности только заданного радиуса, Наконец, и эта проблема была решена – к одной дощечке прикрепили другую и скрепили их между собой. Таким образом и получился первый циркуль.

Видео:Древние строили такое, что не под силу современной технике. Откуда предки черпали знания.Док. фильмСкачать

Строение циркуля

Принцип работы циркуля и его строение остался неизменным на протяжении нескольких сотен лет. Современные технологии лишь сделали этот прибор более удобным для использования. В наше время циркуль состоит из таких частей:

— держатель. Самая верхняя часть циркуля. Главное предназначение держателя – не допустить скольжения руки при выполнении чертежа. Поэтому держатели и делают шероховатыми или со специальными выемками для пальцев;

— штанги. Это основная рабочая часть циркуля, его «ноги». Профессиональные чертежники предпочитают циркули, в которых штанги изготовлены из высокопрочных металлов. Это обеспечивает твердость линии и минимальную погрешность при использовании прибора. А для чего нужен циркуль с пластмассовыми или деревянными штангами? В детских и школьных инструментах высокая точность не требуется, поэтому такие циркули могут изготавливаться из пластмассы;

— игла. Должна быть очень прочной и острой, чтобы максимально крепко закрепить циркуль в точке отсчета и снизить вероятность соскальзывания инструмента с чертежа;

— насадки. Обычно насадками выступают грифельные стержни различной жесткости. Чертежник подбирает жесткость грифеля в зависимости от типа выполняемой работы.

Видео:Геометрия 7 класс. Урок 1 "Первые ученые"Скачать

Использование циркуля в геометрии

Над ответом на вопрос о том, для чего нужен циркуль, никто не задумывается долго. Этот предмет знаком даже школьникам младших классов. Главное, для чего нужен циркуль – чертить окружности различных размеров. Школьники постарше уже знают, что циркулем не только чертят окружности, но и решают множество различных геометрических задач.

Например, разделить отрезок на две равные части без чертежных инструментов очень сложно. Использовав циркуль, можно разделить отрезок на две абсолютно одинаковых по длине части. Как видно, для такой операции нужно точки, обозначающие концы отрезка, сделать центрами пересекающихся окружностей. Через точки пересечения этих окружностей по хорде проведем линию. Точка пересечения линии и заданного отрезка разделит этот отрезок ровно пополам.

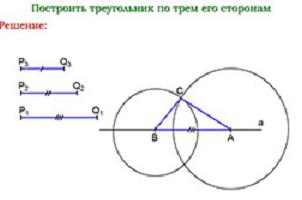
Вот еще один пример того, для чего нужен циркуль. Допустим, заданы стороны треугольника, который нужно построить на бумаге. «На глаз» невозможно определить правильные углы, который будет иметь такой треугольник.

Теперь вы имеете представление о том, для чего нужен циркуль. Картинки, представленные выше, иллюстрируют его использование.

Видео:Построение недостающих проекции сквозного отверстия в сфереСкачать

Использование циркуля -измерителя

С древних времен циркуль расширил сферы своего применения. Например, встречается этот инструмент вовсе без грифеля или карандаша – на обеих ножках его -острые иглы. Можно спросить, для чего нужен циркуль без грифеля? Любой инженер скажет, что это –циркуль-измеритель. Он не предназначен для вычерчивания окружностей и эллипсов, но имеется в каждой готовальне. Для чего нужен циркуль измеритель? С помощью него можно быстро и точно отмерить на чертеже одинаковые расстояния или выполнить разметку чертежа с помощью почти невидимых царапин на бумаге.

Видео:Геометрия 7 класс (Урок№1 - Прямая и отрезок.)Скачать

Использование циркуля землемерами

Используют циркуль и землемеры. Только у них он большой, и расстояние между его штангами строго определено – обычно это один метр. Шагая вместе с таким циркулем, землемер может точно определить размеры участка земли, ведь с каждым шагом землемера такой циркуль отмеряет один погонный метр площади.

Данные примеры лишь в малой степень дают понятие того, для чего нужен циркуль. Ответы, более глубокие и развернутые, могут предложить математики, геологи, инженеры, строители и люди других профессий.

🎦 Видео

ПРИЕМЫ РАБОТЫ С ЧЕРТЕЖНЫМ ИНСТРУМЕНТОМ. Линии чертежа. Видео для начинающихСкачать

Деление окружности на 9 частей циркулем - (Dividing a circle into 9 parts)Скачать

ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Технологии древних строителей раскрыты. Что скрывают каменные строения древних. Док. фильм.Скачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Геометрия 7. Урок 2 - определения. Луч и отрезок.Скачать

Построить угол , равный данному.Скачать

Геометрия 7 класс Урок 2 ФигурыСкачать