Пересекающиеся прямые в треугольнике (3 видео)

Ззамечательные точки треугольника — свойства, применение и примеры решения

Замечательные точки треугольника не просто так описываются таким прилагательным. Для многих учеников, а начинают знакомиться с этим понятием в 8 классе, эта тема кажется наиболее интересной и простой в курсе геометрии, поэтому многочисленные теоремы и свойства запоминаются достаточно просто.

Итак, какие же четыре точки называются замечательными? Перечислим их:

точку пересечения медиан треугольника;

точку пересечения биссектрис треугольника;

точку пересечения высот треугольника;

точку пересечения серединных перпендикуляров сторон треугольника.

Все точки обладают своими особенностями и свойствами, про всех есть свои теоремы и следствия из них. Кроме того, существует свойство, которое справедливо сразу для четырёх этих точек. Вне зависимости от того, медиана ли это, биссектриса или высота, все они пересекаются в одной точке.

Замечательные точки характерны не только для треугольников. Например, в трапеции так же четыре замечательные точки.

Теперь рассмотрим основные положения, связанные с замечательными точками треугольника.

Содержание

Точка пересечения медиан треугольника
Точка пересечения биссектрис треугольника
Точка пересечения высот треугольника
Пример решения задач с построением
Треугольник. Медиана, биссектриса, высота, средняя линия.
теория по математике 📈 планиметрия
Виды треугольников по углам
Виды треугольников по сторонам
Медиана, биссектриса, высота, средняя линия треугольника
Медиана
Биссектриса
Высота
Средняя линия
Урок геометрии «Замечательные точки и линии треугольника»
📸 Видео

Видео:№212. Прямые, содержащие высоты АА1 и ВВ1 треугольника АВС, пересекаются в точке Н, угол В - тупой,Скачать

Точка пересечения медиан треугольника

Из курса геометрии известно определение медианы треугольника.

На данном рисунке она обозначена прямой m, которая исходит из вершины А и заканчивается точкой М, являющейся центром стороны ВС.

Теперь сделаем чертёж треугольника, на котором укажем замечательную точку пересечения медиан.

Для начала постройте абсолютно любой треугольник и обозначьте его буквами А, В и С.

На отрезке АВ отметьте центр С1, на стороне ВС центр А1, на АС центр В1.

Проведите 3 медианы из вершин. Из угла А – медиана АА1,из угла В — медиана ВВ1, из угла С — медиана СС1.

Должно получиться так, как показано на рисунке: три проведённые линии пересекаются в одной точке G (что является их свойством).

Изучим следующее свойство точки пересечения трёх медиан треугольника.

Отрезки медианы треугольника, разделённой замечательной точкой, относятся друг к другу как 2:1. Проследим это свойство на примере используемого нами рисунка:

A1G = 2AG, B1G = 2BG, C1G = 2CG.

Видео:Перпендикулярные прямые. 6 класс.Скачать

Точка пересечения биссектрис треугольника

Прежде чем мы приступим к изучению следующей точки, рассмотрим теорему о биссектрисе, проведённой из вершины неразвёрнутого угла, и докажем её.

Рассмотрим пример. Дано:

угол ВАС Точка пересечения серединных перпендикуляров сторон треугольника

Для начала вспомним определение серединного перпендикуляра. Теорема о серединном перпендикуляре:

Сделаем краткое доказательство. Соединим концы отрезка с вершиной серединного отрезка. Докажем равенство полученных треугольников, из чего следует АD = DB.

Построим эту точку.

В треугольнике АВС отмечаем середины его сторон. Проводим три серединных перпендикуляра КО, LO, МО и отмечаем точку их пересечения О.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Точка пересечения высот треугольника

Проведём три высоты в ∆АВС, все они пересекутся в т. Н. Точка Н по отношению к ∆АВС – ортоцентр.

Свойство высот треугольника:

если все три высоты треугольника или их продолжения пересекаются в одной точке, то это ортоцентр;

СH * HНС
= АH * АНА = ВH * ВНВ.

Ортоцентр может располагаться внутри треугольника, снаружи или совпадать с одной из вершин.

На рисунке показано расположение ортоцентра в остроугольном, прямоугольном и тупоугольном треугольниках.

Видео:Пересекающиеся прямыеСкачать

Пример решения задач с построением

Замечательные точки треугольника замечательные именно потому, что они имеют много полезных для решения задач свойств. Рассмотрим пример решения задачи на эту тему.

Серединный перпендикуляр в ∆АВС, опущенный к АС, пересекает ВС в т. В. Найти BD, DC, если AD = 5 см BC = 9 см.

Сделаем дополнительное построение – серединный отрезок КD к прямой АС. Тогда DK это и высота, и медиана в ∆АВС. Если в треугольнике проведена прямая, которая является высотой и медианой, то он равнобедренный. Значит, AD = DC = 5 см.

ВD =ВС — DC = 4 см.

Ответ: DC = 5 см, ВD = 4 см.

Видео:Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

Треугольник. Медиана, биссектриса, высота, средняя линия.

теория по математике 📈 планиметрия

Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.

Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.

Виды треугольников по углам

Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.

Остроугольные	Тупоугольные	Прямоугольные
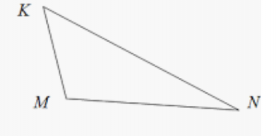
Остроугольным треугольником называется треугольник, у которого все три угла острые. На рисунке показан такой остроугольный треугольник АВС.	Тупоугольным называется треугольник, у которого есть тупой угол. В треугольнике может быть только один тупой угол. На рисунке показан треугольник такого вида, где угол М – тупой.	Прямоугольным называется треугольник, у которого есть угол, равный 90 0 (прямой угол). На рисунке угол С равен 90 0 . Такой угол в любом прямоугольном треугольнике – единственный.

Виды треугольников по сторонам

Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.

Разносторонний	Равнобедренный	Равносторонний
Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС.	Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС.	Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Медиана, биссектриса, высота, средняя линия треугольника

Медиана

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.

По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.

Биссектриса

Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.

В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD₁, EE₁ и CC₁.

По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.

Высота

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.

На рисунке показаны высоты треугольника АВС: АН₁, ВН₂ и СН₃.

По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.

Средняя линия

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.

Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.

Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 90 0 .

Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.

Составим отношение сторон:

A E A B . . = A B A F . . откуда по свойству пропорции АВ 2 =АЕ ∙ АF

Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.

Составим отношение сторон:

A E A D . . = A C A F . . ; откуда выразим AD= A E ∙ A F А C . . = A E ∙ A F A C . .

Теперь рассмотрим наши два полученных равенства: АВ 2 =АЕ ∙ АF и AD= A E ∙ A F A C . .

Видим, что 36 2 =АЕ ∙ АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD= A E ∙ A F A C . . = 36 2 54 . . = 24

Теперь найдем CD=AC-AD=54-24=30

pазбирался: Даниил Романович | обсудить разбор | оценить

На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.

pазбирался: Даниил Романович | обсудить разбор | оценить

В треугольнике АВС известно, что угол ВАС равен 84 0 , АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0

pазбирался: Даниил Романович | обсудить разбор | оценить

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Урок геометрии «Замечательные точки и линии треугольника»

Разделы: Математика

Цели урока.

Обобщить и систематизировать знания по ранее изученному материалу.

Познакомить учащихся с теоремами Чевы и Менелая.

Сформировать умения решать ключевые задачи темы.

Удивительно, но треугольник, несмотря на свою кажущуюся простоту, является неисчерпаемым объектом изучения — никто даже в наше время не осмелится сказать, что изучил и знает все свойства треугольника. Действительно, кто не слышал о Бермудском треугольнике, в котором бесследно исчезают корабли и самолёты? А ведь сам треугольник таит в себе немало интересного и загадочного.

Тема нашего сегодняшнего урока “Замечательные точки и линии треугольника”.

Вспомним материал, который изучали ранее на уроках. С какими замечательными точками треугольника мы были знакомы ранее? (Учащиеся отвечают)

К числу таких точек, изучаемых в школьном курсе геометрии относятся:

точка пересечения биссектрис (центр вписанной окружности);
точка пересечения серединных перпендикуляров (центр описанной окружности треугольника);
центр пересечения высот треугольника (ортоцентр);
точка пересечения медиан (центроид).

Если рассмотреть дополнительно биссектрисы трех пар внешних углов треугольника, то получается еще три замечательные точки – центры вневписанных окружностей:

В треугольнике ABC точка D делит сторону BC в отношении BD:DC= 1: 3, а точка O делит AD в отношении AO:OD=5:2. В каком отношении прямая BO делит отрезок AC? (Подсказка: сделать дополнительное построение и использовать теорему Фалеса).

ABC, DBC, BD : DC= 1:3

OAD, AO : OD= 5:2

BO AC= E

Проведем DM ll BE . По теореме Фалеса . Тогда AE= 5k, EM= 2k, где k — коэффициент пропорциональности. Аналогично , откуда MC= 3EM=6k; EC= 2k+6k= 8k; .

Ответ: AE : EC= 5:8

Для решения этой задачи пришлось выполнить дополнительное построение. Эту задачу можно решить без дополнительного построения, причем достаточно просто и быстро. Но для этого нам понадобится следующее утверждение:

Теорема (Менелая). Пусть на сторонах AB, BC и на продолжении стороны AC ABC взяты соответственно точки C₁, A₁, B₁, не совпадающие с вершинами треугольника. Если точки A₁, B₁, C₁ лежат на одной прямой, то выполняется равенство

..=1 ()

Точка C₁ – середина стороны AB треугольника ABC. Точка O – середина отрезка CC₁. В каком отношении делит прямая AO сторону BC?

Точка A₁ делит сторону BC треугольника ABC в отношении 1:2. Точка B₁ делит сторону AC в отношении 2:1. Прямая A₁B₁ пересекает продолжение стороны AB в точке C₁. Найдите отношение AB:BC₁.

Мы знаем, что медианы треугольника пересекаются в одной точке, биссектрисы треугольника пересекаются в одной точке, высоты треугольника (или их продолжения) пересекаются в одной точке. Поставим теперь общий вопрос. Рассмотрим ABC и отметим на его сторонах BC, AC и AB (или их продолжениях) соответственно точки L, M, K. При каком расположении этих точек прямые AL, BM и CK пересекутся в одной точке?

Ответ на этот вопрос нашел в 1678 году итальянский инженер-гидравлик Джованни Чева (1698–1734 гг.). Чева создал учение о секущих, положившее начало новой синтетической геометрии. Известна его работа “О взаимном расположении пересекающихся прямых” (1678 г.) и теорема Чевы о соотношениях отрезков в треугольнике.

Точки C₁ и A₁ делят стороны AB и BC треугольника ABC в отношении 1:2. Прямые CC₁ и AA₁ пересекаются в точке O. Найдите отношение, в котором прямая BO делит сторону CA.

Решение: По условию задачи

Используя теорему Чевы, находим

Точки C₁, B₁, A₁ делят стороны AB, AC, BC, соответственно, в отношениях 4:1, 2:1, 1:2. Выясните, пересекаются ли прямые AA₁, BB₁, CC₁ в одной точке (Да).

Сегодня на уроке мы с вами рассмотрели две замечательные теоремы планиметрии – теоремы Чевы и Менелая. Применение теорем Чевы и Менелая для позволяет получить решение многих стандартных и известных задач не менее простые и компактные, но и более эффективные.