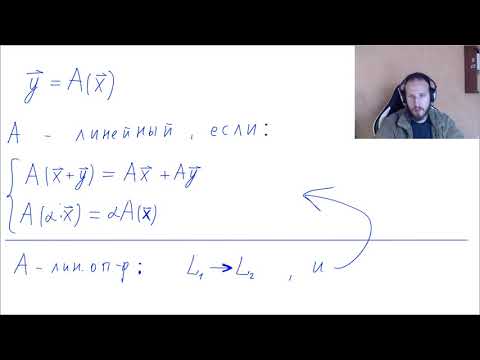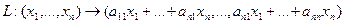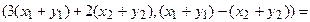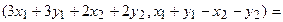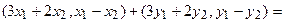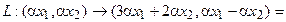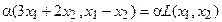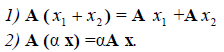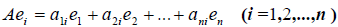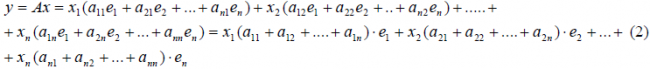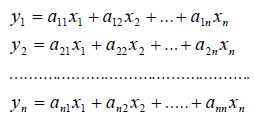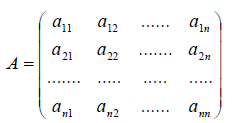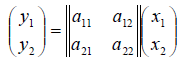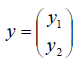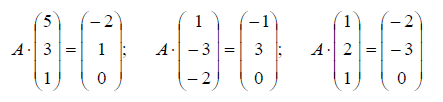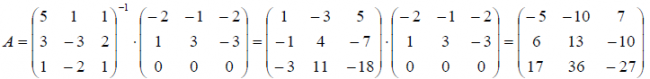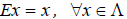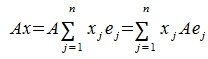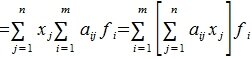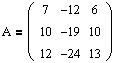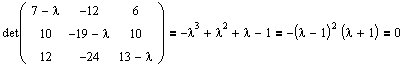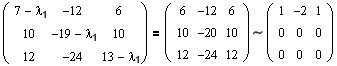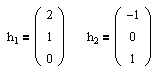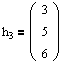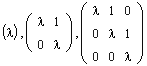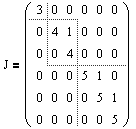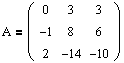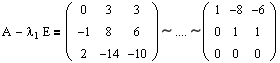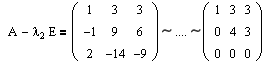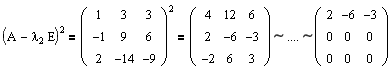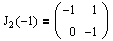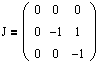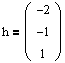- Построение матрицы по заданной формуле отображения.
- Матрица линейного оператора
- Примеры линейных операторов
- Действия над операторами
- 1. Понятие линейного оператора
- 2. Сложение линейных операторов
- 3. Умножение линейных операторов
- 4. Умножение линейного оператора на число
- 5. Нулевой оператор
- 6. Противоположный оператор
- 7. Ядро линейного оператора
- 8. Образ линейного оператора
- 9. Ранг линейного оператора
- Матрица линейного отображения
- Свойства матриц линейных отображений
- Алгоритм нахождения векторов жорданова базиса
- 🎬 Видео
Видео:Собственные векторы и собственные значения матрицыСкачать

Построение матрицы по заданной формуле отображения.
Пусть отображение задано с помощью формулы:
то есть для координат произвольного исходного вектора определены координаты его образа. Тогда, рассматривая вместо произвольного вектора x вектор 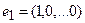
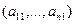
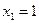
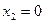
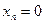
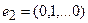
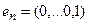
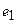
Пример 1. Пусть оператор задан с помощью формулы:
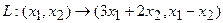
Прежде всего, докажем, что это отображение – действительно линейный оператор.
Отобразим сумму векторов:
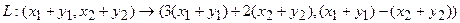
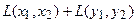
Аналогично для умножения на константу:
Для того чтобы найти матрицу этого линейного оператора, нужно, как было сказано выше, подставить значения x1 = 1, x2 = 0, а затем x1 = 0, x2 = 1. В этом примере образы базисных векторов – соответственно (3, 1) и (2, -1).
Поэтому матрица линейного оператора будет иметь вид:
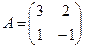
Аналогичным способом решается задача и для 3 и большего количества переменных.
Пример 2. 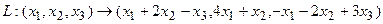
Построим матрицу оператора. Отображая вектор (1,0,0), получаем (1,4,-1), соответственно (0,1,0) переходит в (2,1,-2), а вектор (0,0,1) – в (-1,1,3).
Матрица линейного оператора:
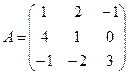
2.2. Построение матрицы оператора в случае, когда известен исходный базис и система векторов, в которую он отображается.
Если задана система 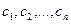
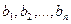
Матрицу этого оператора можно найти двумя способами: с помощью обратной матрицы и с помощью системы уравнений.
Пусть 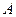
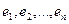
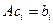
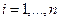
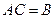
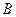
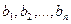
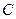
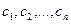
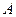
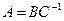
Пример. Найти матрицу линейного оператора, отображающего базис
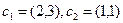
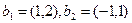
Здесь 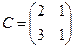
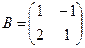
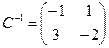
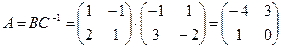
Проверка осуществляется умножением получившейся матрицы на каждый вектор: 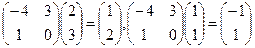
Аналогично решаются подобные задачи и для трёхмерного пространства. В приложении (§5) есть несколько вариантов таких задач.
2.3. Прочие способы нахождения матрицы оператора.
Существуют также примеры, где линейный оператор задаётся другими способами, отличными от рассмотренных в п. 2.1 и 2.2.
Пример. Линейными операторами являются как правое, так и левое векторное умножение на фиксированный вектор в трёхмерном пространстве, то есть отображения вида 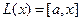
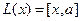
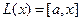
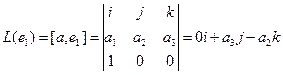
Аналогично, 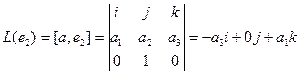
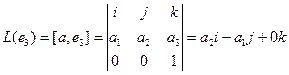
Координаты полученных векторов запишем в виде столбцов матрицы оператора.
Матрица оператора: 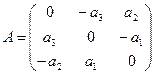
Аналогично можно построить матрицу линейного оператора 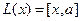
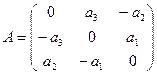
Пример. Линейный оператор дифференцирования в пространстве всех многочленов степени не более n. Это пространство размерности n + 1. Возьмём в качестве базиса элементы 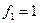
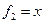
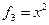
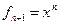
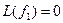
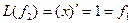
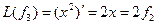
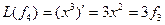
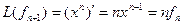
Матрица этого линейного оператора:
Линейные операторы могут отображать не только пространства конечной размерности, но и бесконечномерные пространства. Так, оператор дифференцирования может рассматриваться также в пространстве всех непрерывных функций. (В этом пространстве нет конечного базиса). В этом случае, очевидно, оператор не может быть задан матрицей конечного порядка.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10219 – 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Видео:Ядро и образ линейного оператораСкачать

Матрица линейного оператора
Определение 1. Если задан закон, который каждому вектору x?? ставит в соот ветствие вектор y . то говорят, что в линейном пространстве ? задан оператор A , при этом пишут:
Определение 2. Оператор A называется линейным, если для любых x 1 ?? и x 2 ?? и произвольного числа ? выполняются условия:
Рассмотрим теперь в евклидовом пространстве E n базис e 1 ,e 2 . e n и пусть в этом пространстве определён линейный оператор A : y = A x .
Разложим векторы x и y по базису e 1 ,e 2 . e n :
В силу линейности оператора A можно написать
Заметим, что каждый вектор 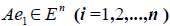
В силу единственности разложения по данному базису мы можем при равнять коэффициенты при базисных векторах в правых частях формул (1) и (2); тогда получим:
Получили, что линейному оператору A в данном базисе соответствует квадратная матрица
которая называется матрицей линейного оператора A , i -й столбец которой состоит из координат вектора Ae i (i = 1,2. n ) относительно данного базиса. Отметим, что матрица A оператора A зависит от выбора базиса e 1 ,e 2 . e n .
Итак, мы показали, что всякому линейному оператору A в евклидовом пространстве E n соответствует матрица A ; можно доказать и обратное утверждение: всякую квадратную матрицу A можно рассматривать как матрицу некоторого линейного оператора A в данном базисе e 1 ,e 2 . e n .
Представляют интерес невырожденные линейные операторы, т.е. такие операторы, матрицы которых имеют обратную A -1 , т.е. также являются невырожденными. В этом случае каждому вектору y (образу), определённому соотношением, отвечает единственный вектор x (прообраз) и при этом имеет место матричное равенство: X = A -1 ? Y .
Видео:Матрица линейного оператораСкачать

Примеры линейных операторов
1. В пространстве 2-мерных векторов линейным оператором является правило
связывающее вектор-прообраз 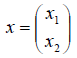
2. В пространстве бесконечно дифференцируемых функций линейным оператором является операция дифференцирования, ставящая в соответствие каждому элементу этого простран ства его производную функцию.
3. В пространстве многочленов P n (t) линейным оператором является операция умножения многочлена на независимую переменную t .
Пример: Известны образы базисных векторов E 3 под действием оператора A :
Найти матрицу этого оператора в исходном базисе.
Решение: По определению y = A x, значит в матричном виде можно записать, что A = X -1 Y . Для нашего примера получаем
Видео:Собственные векторы и собственные числа линейного оператораСкачать

Действия над операторами
Сложение линейных операторов. Пусть x?E n , A и B – два линейных оператора в этом пространстве.
Определение 1. Суммой линейных операторов A и B в E n называется оператор C, определяемый равенством Cx = A x + Bx , где x – любой вектор из E n .
Сумма линейных операторов является линейным оператором, причём его матрица C = A + B, где A и B – матрицы линейных операторов A и B .
Умножение линейного оператора на число. Пусть x?E n , линейный оператор A определён в E n , ? – некоторое число.
Определение 2. Произведением линейного оператора A на число ? называется оператор ?A , определяемый равенством 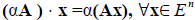
?A является линейным оператором, а матрица этого линейного оператора получается из матрицы A умножением её на число ? , т.е. она равна ? ? A.
Умножение линейных операторов. Пусть x? E n , y ? E n , z ? E n и кроме того в E n определены линейные операторы A и B таким образом, что y = Bx, z = A y .
Определение 3. Произведением A ? B линейных операторов A и B называется оператор C, определяемый соотношением Cx = A (Bx) .
Таким образом, перемножение линейных операторов состоит в последовательном их применении по отношению к вектору x .
Рассмотрим матрицы – столбцы:
и обозначим через A, B и C – соответственно матрицы линейных операторов A, B и C. Тогда Z = A ? (B ? X) = (A ? B) ? X = C ? X , таким образом, C = A ? B, т.е. матрица произведения линей ных операторов также является линейным оператором.
a) (A ? B)(x + y) = A (B(x + y)) = A (Bx + By) = A (Bx) + A (By) = = (A ? B) ? x + (A ? B) ? y
б) (A ? B)(? x) = A (B(? x)) = A (?Bx) =?A (Bx) =? (A ? B)x
Свойства умножения линейных операторов вытекают из свойств умножения матриц.
Определение 4. Линейные операторы A и В называются равными, если 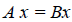
Определение 5. Оператор E называется единичным (или тождественным) оператором, если каждому элементу x линейного пространства 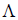
Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

1. Понятие линейного оператора
Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида 
Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x1 и x2 пространства R и любого λ из числового поля K выполняются соотношения
Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.
Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы 

| y=Ax, | (1) |
где A – m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:
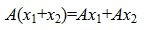 , , | (2) |
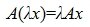 . . |
Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов 

Пусть x − произвольный элемент в R. Тогда
 | (3) |
является разложением x в по базису 
Применим оператор A к базисным векторам 
 | (4) |
где aij − координаты полученного вектора в базисе 
Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем
Сделаем следующее обозначение:
 | (6) |
Тогда равенство (5) примет следующий вид:
 | (7) |
Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе 
Построим матрицу A с элементами aij:
 | (8) |
Тогда выражение (6) можно записать в матричном виде:
| y=Ax. | (9) |
Матрица A называется матрицей линейного оператора в заданных базисах 

Видео:Координаты в новом базисеСкачать

2. Сложение линейных операторов
Пусть A и B два линейных оператора действующих из R в S и пусть A и B – mxn − матрицы соответствующие этим операторам.
Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством
| Cx= Ax+ Bx, x∈R, | (10) |
где x∈R означает, что x принадлежит пространстве R.
Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.
Применим оператор C к базисному вектору ej, тогда:
| Cej= Aej+ Bej= | n | (aij+bij) ej |
| ∑ | ||
| j= 1 |
Следовательно оператору C отвечает матрица 
| C=A+B. | (11) |
Видео:Как разложить вектор по базису - bezbotvyСкачать

3. Умножение линейных операторов
Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.
Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:
| Cx= A( Bx), x ∈ R. | (12) |
Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.
Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C
| y=Bx, z=Ay, z=Cx |
можно записать в виде матричных равенств
| y=Bx, z=Ay, z=Cx |
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
| Cx=A(Bx)=(AB)x. |
Учитывая произвольность х, получим
| C=AB. | (13) |
Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.
Видео:Собственные значения и собственные векторы матрицы (4)Скачать

4. Умножение линейного оператора на число
Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.
Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:
| Cx=λ ( Ax) | (14) |
Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства
| y=Ax, z=λy, z=Cx |
можно записать в виде матричных равенств
| y=Ax, z=λy, z=Cx |
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
| Cx=λ(Ax)=(λA)x. |
Учитывая произвольность х, получим
| C=λA. | (15) |
Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.
Видео:Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать

5. Нулевой оператор
Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:
Видео:Матрица переходаСкачать
6. Противоположный оператор
Противоположным оператору A называется оператор −A удовлетворяющий равенству:
Видео:Собственные значения и собственные векторыСкачать

7. Ядро линейного оператора
Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.
Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.
Видео:Матрицы и векторыСкачать

8. Образ линейного оператора
Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.
Образ линейного оператора обозначается символом im A.
Видео:Проверить, что отображение является линейным оператором. Найти ядро, образ, ранг, дефект, матрицу.Скачать

9. Ранг линейного оператора
Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).
Видео:Образ линейного оператора. ПримерСкачать

Матрица линейного отображения
Пусть — линейное отображение n-мерного пространства в m-мерное пространство . Зафиксируем в пространстве произвольный базис , а в пространстве базис . Линейное отображение однозначно задается образами базисных векторов (см. свойство 6). Разложим образы , базисных векторов по базису
Из координатных столбцов векторов относительно базиса составим матрицу размеров
Она называется матрицей линейного отображения в базисах и . Матрицу отображения обозначают также , чтобы подчеркнуть ее зависимость от выбранных базисов.
При помощи матрицы отображения найдем координаты образа по координатам прообраза . Пусть — координатный столбец вектора , а — координатный столбец вектора , т.е. и . Тогда
В силу единственности разложения вектора по базису получаем
Используя матричные операции, связь координат можно записать в виде
где — матрица (9.1) отображения .
Таким образом, для каждого линейного отображения n-мерного пространства в m-мерное пространство (с фиксированными базисами и соответственно) определена единственная матрица (9.1) этого отображения, и наоборот, любая числовая матрица размеров является матрицей некоторого линейного отображения n-мерного пространства в m-мерное пространство .
Для нахождения матрицы отображения нужно выполнить следующие действия:
1) зафиксировать базисы и пространств и
2) найти образ первого базисного вектора и разложить его по базису . Полученные координаты записать в первый столбец матрицы (9.1) отображения ;
3) найти образ второго базисного вектора и разложить его по базису . Полученные координаты записать во второй столбец матрицы (9.1) отображения и т.д. В последний столбец матрицы (9.1) записать координаты образа последнего базисного вектора.
Найдем матрицы отображений, рассмотренных выше.
1. Матрица нулевого отображения нулевая относительно любых базисов пространств и , так как образ любого базисного вектора равен нулевому вектору , координаты которого равны нулю (относительно любого базиса пространства ).
2. Пусть в n-мерном линейном пространстве задан базис . Рассмотрим отображение , которое ставит в соответствие каждому вектору его координатный столбец относительно заданного базиса. В пространстве выберем стандартный базис . Напомним, что в стандартном базисе координатный столбец вектора совпадает с самим столбцом , так как
Поэтому образ первого базисного вектора имеет координатный столбец , совпадающий с первым базисным вектором . Образ и т.д. Составляя из этих столбцов матрицу отображения , получаем единичную матрицу n-го порядка.
3. В n-мерном евклидовом пространстве возьмем ортонормированный базис . В качестве базиса одномерного линейного пространства возьмем единицу. Рассмотрим отображение , где — алгебраическое значение проекции вектора на направление, задаваемое вектором . Тогда матрица отображения имеет вид , так как , а для .
4. Взяв в пространствах и стандартные базисы, находим образы базисных векторов (первые производные многочленов):
Записывая найденные координаты по столбцам матрицы отображения, получаем матрицу размеров
Видео:Образуют ли данные векторы базисСкачать

Свойства матриц линейных отображений
При фиксированных базисах линейных пространств:
1) матрица суммы линейных отображений равна сумме их матриц;
2) матрица произведения линейного отображения на число равна произведению матрицы отображения на то же самое число;
3) матрица обратного отображения является обратной для матрицы отображения;
4) матрица композиции отображений равна произведению матриц отображений: .
Докажем, например, последнее свойство. Пусть в линейных пространствах фиксированы базисы соответственно. Отображения , , а также их композиция , имеют матрицы относительно соответствующих базисов. Для координатных столбцов векторов запишем связи (9.2): . Тогда для координатного столбца произвольного вектора . Отсюда следует, что .
Видео:Базис и матрица перехода. Координаты вектора в разных базисах.Скачать

Алгоритм нахождения векторов жорданова базиса
Собственные векторы и собственные значения
Пусть A – матрица некоторого линейного преобразования порядка n.
Определение. Многочлен n-ой степени
P(l)=det(A-lЕ) (1.1)
называется характеристическим многочленом матрицы А, а его корни, которые могут быть как действительными, так и комплексными, называются характеристическими корнями этой матрицы.
Определение. Ненулевой вектор x линейного пространства V, удовлетворяющий условию
А(х)=lх, (1.2)
называется собственным вектором преобразования A. Число l называется собственным значением.
Замечание. Если в пространстве V задан базис, то это условие можно переписать следующим образом:
Ах=lх, (1.3)
где A – матрица преобразования, x – координатный столбец.
Определение. Алгебраической кратностью собственного значения lj называется кратность корня lj характеристического многочлена.
Определение. Совокупность всех собственных значений называется спектром матрицы.
Алгоритм нахождения собственных значений и собственных векторов
1. Найти собственные значения матрицы:
· записать характеристическое уравнение:
det(A-lЕ)=0; (1.4)
· найти его корни l j, j=1. n и их кратности.
2. Найти собственные векторы матрицы:
· для каждого l j решить уравнение
· найденный вектор х и будет собственным вектором, отвечающим собственному значению l j.
Пример1
Найдем собственные значения и собственные векторы, если известна матрица преобразования:
Записываем характеристический многочлен (1.1) и решаем характеристическое уравнение (1.4):
Получаем два собственных значения: l1=1 кратности m1=2 и l2=-1 кратности m2=1.
Далее с помощью соотношения (1.5) находим собственные векторы. Сначала ищем ФСР для l1=1:
Очевидно, что rang=1, следовательно, число собственных векторов для l1=1 равно n-rang=2. Найдем их:
Аналогичным образом находим собственные векторы для l2=-1. В данном случае будет один вектор:
Понятие жордановой клетки и жордановой матрицы
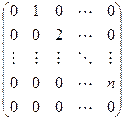
Определение. Жордановой клеткой порядка m, отвечающей собственному значению l, называется матрица вида:
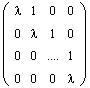
Иными словами, на главной диагонали такой матрицы располагается собственное значение l, диагональ, ближайшая к главной, сплошь занята единицами, а все остальные элементы матрицы равны нулю. Ниже даны примеры жордановых клеток соответственно первого, второго и третьего порядков:
Определение. Блочно-диагональная матрица, на диагонали которой стоят жордановы клетки, называется жордановой матрицей:
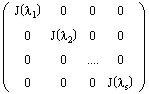
Пример
Ниже представлена жорданова матрица, состоящая из трех жордановых клеток:
— размера 1, отвечающая собственному значению l1=3;
— размера 2, отвечающая собственному значению l2=4;
— размера 3, отвечающая собственному значению l3=5.
Количество и размер жордановых клеток
Пусть А — матрица, которую нужно привести к жордановой форме, lj (k=1. mj) — собственные значения этой матрицы.
Количество жордановых клеток размера k, отвечающих собственному значению lj, определяется следующим образом:
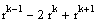
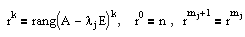
Пример
Пусть дана матрица преобразования:
Найдем количество и размер жордановых клеток, соответствующих каждому собственному значению этого преобразования.
Как искать собственные значения, было подробно рассказано в первом параграфе учебника. Поэтому опустим все расчеты, а сразу укажем собственные числа матрицы А: l1=0 кратности m1=1 и l2=-1 кратности m2=2.
Используя соотношения (3.1) и (3.2), найдем количество и размер жордановых клеток, соответствующих l1=0, m1=1.
Очевидно, что rang(A-l1E)=2 и, соответственно, r 1 =r 2 =rang(A-l1E) 1 =2, r 0 =n=3.
Количество жордановых клеток размера 1 будет равно: r 0 -2r 1 +r 2 =3-2*2+2=1.
Ясно, что других клеток для этого собственного значения нет. Т.о., для l1=0, m1=1 мы имеем единственную жорданову клетку вида J1(0)=(0).
Далее аналогичным образом определяем клетки для второго собственного значения l2=-1 кратности m2=2.
Очевидно, что rang(A-l2E)=2 и, соответственно, r 1 =r 2 =rang(A-l2E) 1 =2.
Т.е. rang(A-l1E) 2 =1 и, соответственно, r 1 =r 2 =rang(A-l1E) 2 =1.
Теперь можно определить количество и размер жордановых клеток для второго собственного значения:
— размера 1: r 0 -2r 1 +r 2 =3-2*2+1=0;
— размера 2: r 1 -2r 2 +r 3 =2-2*1+1=1.
Таким образом, для l2=-1 мы получили одну клетку размера 2:
Соответственно, жорданова форма для исходной матрицы А будет иметь вид:
Жорданов базис
Пусть матрица А приведена к жордановой форме J. Рассмотрим систему HJ=AH, где
— матрица перехода от исходного базиса (e) к жорданову базису (h). Это система матричных n 2 уравнений с n 2 неизвестными.
Определение. Пусть e – собственный вектор преобразования А, т.е. имеет место равенство А(e) = le. Вектор e1, удовлетворяющий равенству
называется присоединенным вектором первого порядка;
вектор e2, удовлетворяющий равенству
— присоединенным вектором второго порядка;
вектор en, удовлетворяющий равенству
— присоединенным вектором n-ого порядка.
Заметим также, что
(А-lе) k ek=e. (4.5)
Алгоритм нахождения векторов жорданова базиса
Чтобы найти жорданов базис, необходимо проделать следующие действия для каждой жордановой клетки.
Рассмотрим жорданову клетку порядка k, отвечающую собственному значению l. Для нее ищутся вектора жорданова базиса:
h, h 1 , h 2 , . h k-1 , где:
h — собственный вектор, отвечающий собственному значению l;
h 1 — присоединенный вектор 1-ого порядка;
h 2 — присоединенный вектор 2-ого порядка;
h k-1 — присоединенный вектор (k-1)-ого порядка;
Эта совокупность векторов ищется, используя следующую систему:
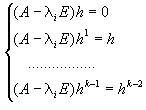
В результате применения этих операций ко всем жордановым клеткам, получим векторы, составляющие жорданов базис:
h, h 1 , h 2 , . h k-1 , f, f 1 , f 2 , . f p-1 .
Векторам h соответствует жорданова клетка размера k, векторам f – размера p и т.д.
ex3
Пример
Вернемся к примеру, рассмотренному в прошлом разделе. Там нами были получены две жордановы клетки:
J1(0)=(0) и
Рассмотрим первую, J1(0).
С помощью соотношения (1.5) из первого параграфа найдем собственный вектор, отвечающий собственному значению l1=0:
Присоединенных векторов для данной жордановой клетки, очевидно, нет.
Теперь рассмотрим вторую жорданову клетку, J2(-1). Очевидно, что для нее надо найти один собственный вектор и один присоединенный.
Используя систему (4.6), получим эти векторы:
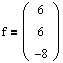
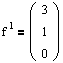
Мы получили все векторы, составляющие матрицу Н. Таким образом, матрица перехода к жорданову базису будет иметь следующий вид:
🎬 Видео
Матрица линейного оператора (01)Скачать

Код сверхспособностей по дате рождения. НумерологияСкачать

10.2 Матрица линейного оператораСкачать

Линейные операторы.Скачать