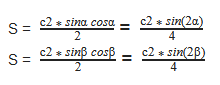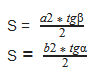- Онлайн калькулятор
- Найти площадь прямоугольного треугольника по двум катетам
- Теория
- Найти площадь прямоугольного треугольника по катету и гипотенузе
- Теория
- Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу
- Теория
- Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу
- Теория
- Найти площадь прямоугольного треугольника зная длину гипотенузы и один из острых углов
- Теория
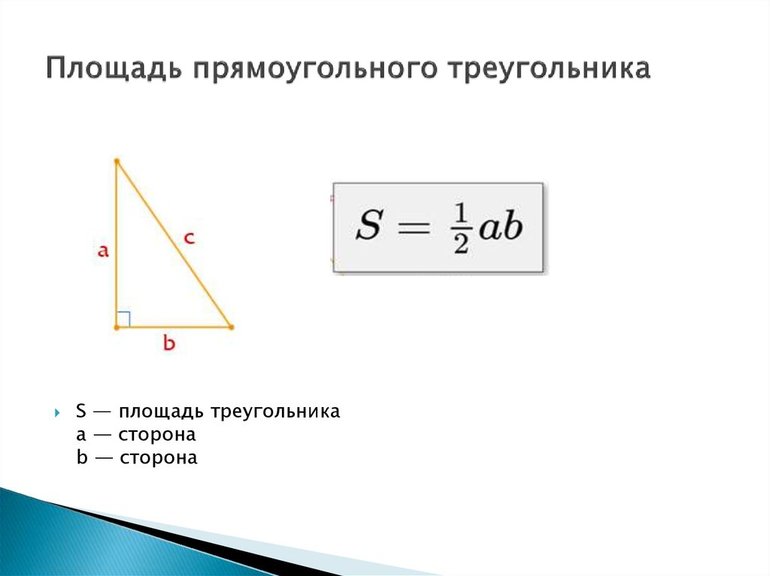
- Площадь прямоугольного треугольника
- Основные определения
- Формула для нахождения площади прямоугольного треугольника через катеты
- Формула для нахождения площади прямоугольного треугольника через гипотенузу
- Формула для нахождения площади прямоугольного треугольника через гипотенузу и острый угол
- Формулы нахождения площади прямоугольного треугольника через катет и угол
- Формулы нахождения площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу
- Площадь прямоугольного треугольника через катеты — формула и примеры расчетов
- Свойства треугольника
- Прямоугольная фигура
- Формулы площади
- Решение задач
- 🔍 Видео
Видео:Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?Скачать

Онлайн калькулятор
Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- длины катетов a и b
- длину гипотенузы с и длину любого из катетов (a или b)
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- длину гипотенузы с и один из острых углов (α или β)
Найти площадь прямоугольного треугольника по двум катетам
Теория
Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?
Формула
Пример
К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:
S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²
Найти площадь прямоугольного треугольника по катету и гипотенузе
Теория
Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?
Формула
S = ½ ⋅ a ⋅ √ c² — a² = ½ ⋅ b ⋅ √ c² — b²
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:
S = 2 ⋅ √ 5² — 2² / 2 = √ 25 — 4 ≈ 4.58 см²
Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу
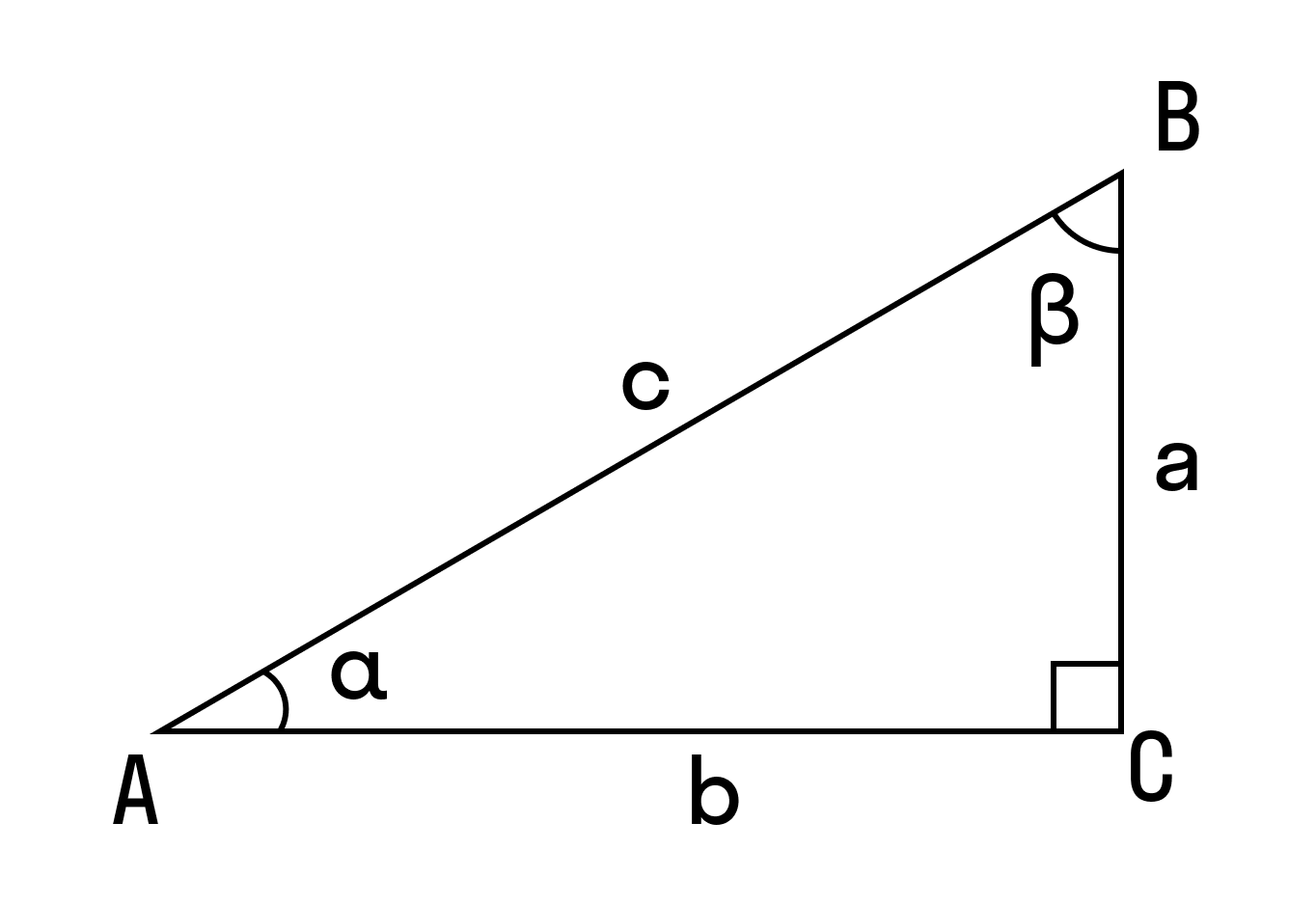
То есть к катету a прилежащий ∠β, а к катету b — ∠α
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:
S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²
Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу
То есть к катету a противолежащий ∠α, а к катету b — ∠β
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(90 — α) = ½ ⋅ b² ⋅ tg(90 — β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:
S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²
Найти площадь прямоугольного треугольника зная длину гипотенузы и один из острых углов
Теория
Чему равна площадь (S) прямоугольного треугольника если известны длина гипотенузы (c) и один из острых углов?
Формула
S = ½ ⋅ c² ⋅ sin(α) ⋅ cos(α) = ½ ⋅ c² ⋅ sin(β) ⋅ cos(β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:
S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²
Видео:КАК НАЙТИ ПЛОЩАДЬ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА? Примеры | МАТЕМАТИКА 5 классСкачать

Площадь прямоугольного треугольника
О чем эта статья:
площадь, 8 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Найдите площадь прямоугольного треугольника, если сумма его катетов равна 15, а гипотенуза равна 13Скачать

Основные определения
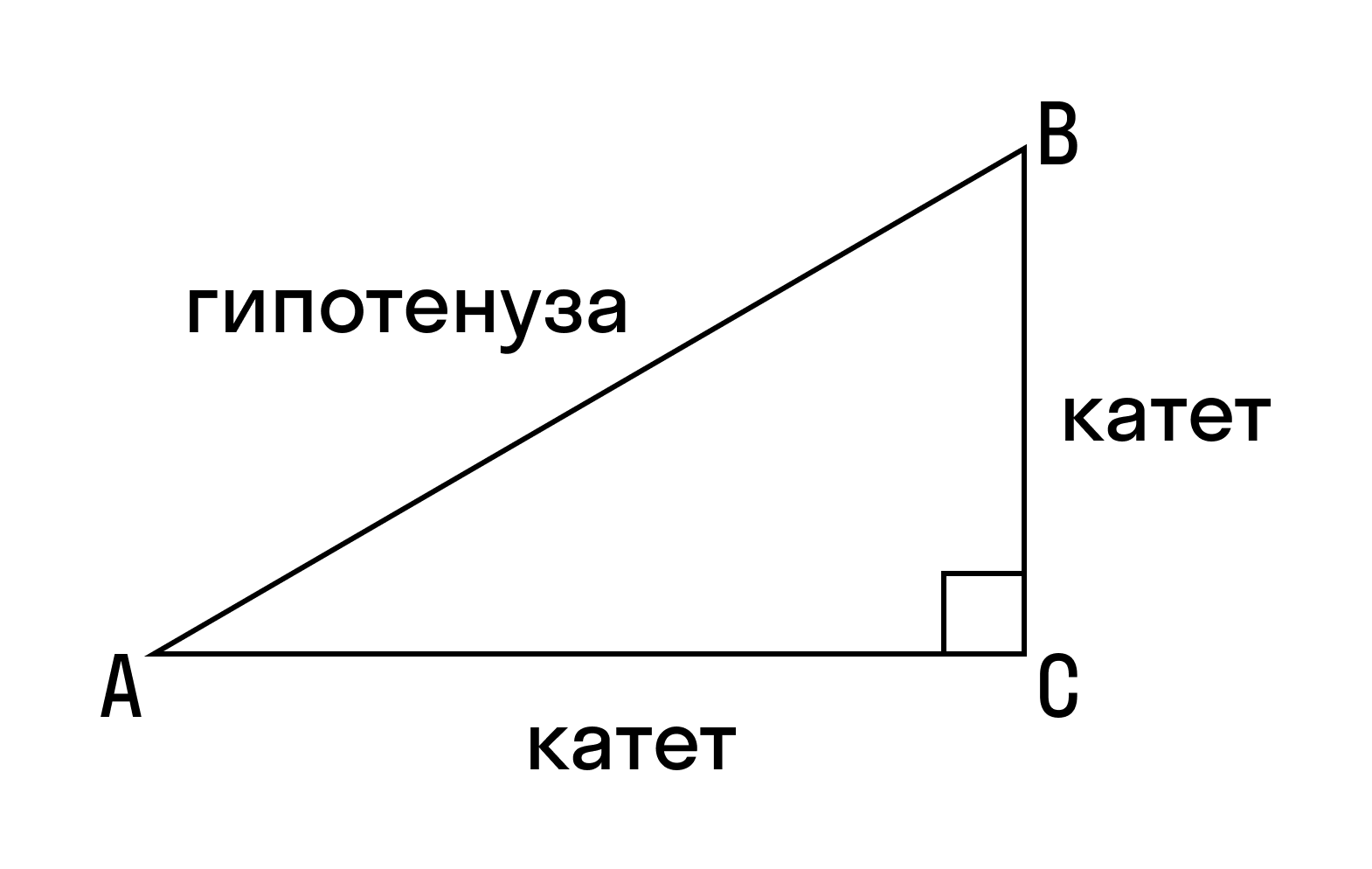
Прямоугольный треугольник — это треугольник, в котором один угол прямой, то есть равен 90˚.
Гипотенуза — это сторона, противолежащая прямому углу.
Катеты — это стороны, прилежащие к прямому углу.
Чтобы найти площадь прямоугольного треугольника, можно применить любую формулу нахождения площади треугольника — их несколько.
Видео:№471. Найдите площадь прямоугольного треугольника, если его катеты равны: а) 4 см и 11см;Скачать

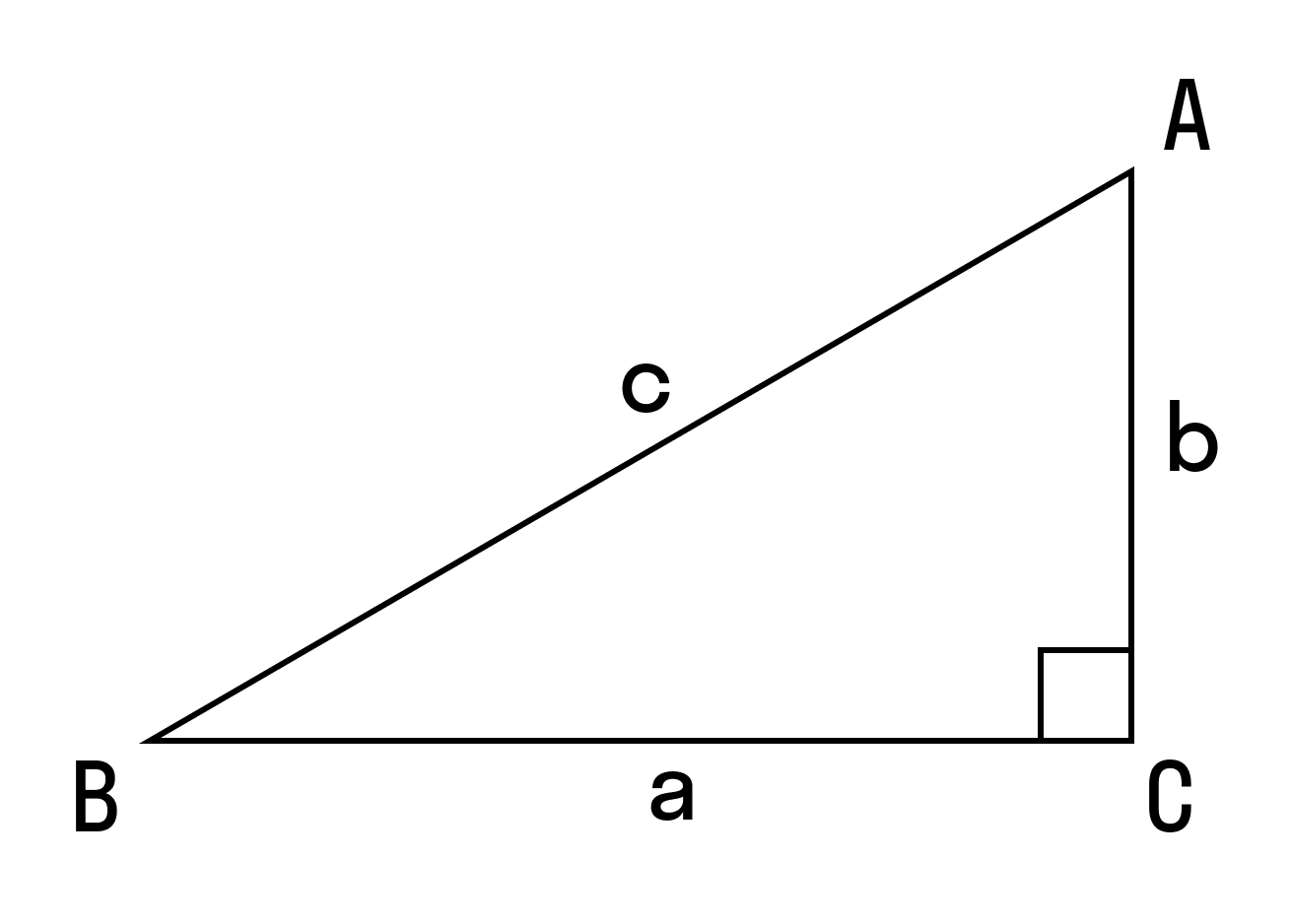
Формула для нахождения площади прямоугольного треугольника через катеты
Чтобы найти площадь, нужно вывести формулу:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию.
Так как в прямоугольном треугольнике катеты перпендикулярны, то один катет — это высота, проведенная ко второму катету.
Отсюда следует, что площадь прямоугольного треугольника равна половине произведения его катетов.
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через катеты.
S = 1/2 (a × b), где a и b — катеты
Видео:Площади фигур. Сохраняй и запоминай!#shortsСкачать

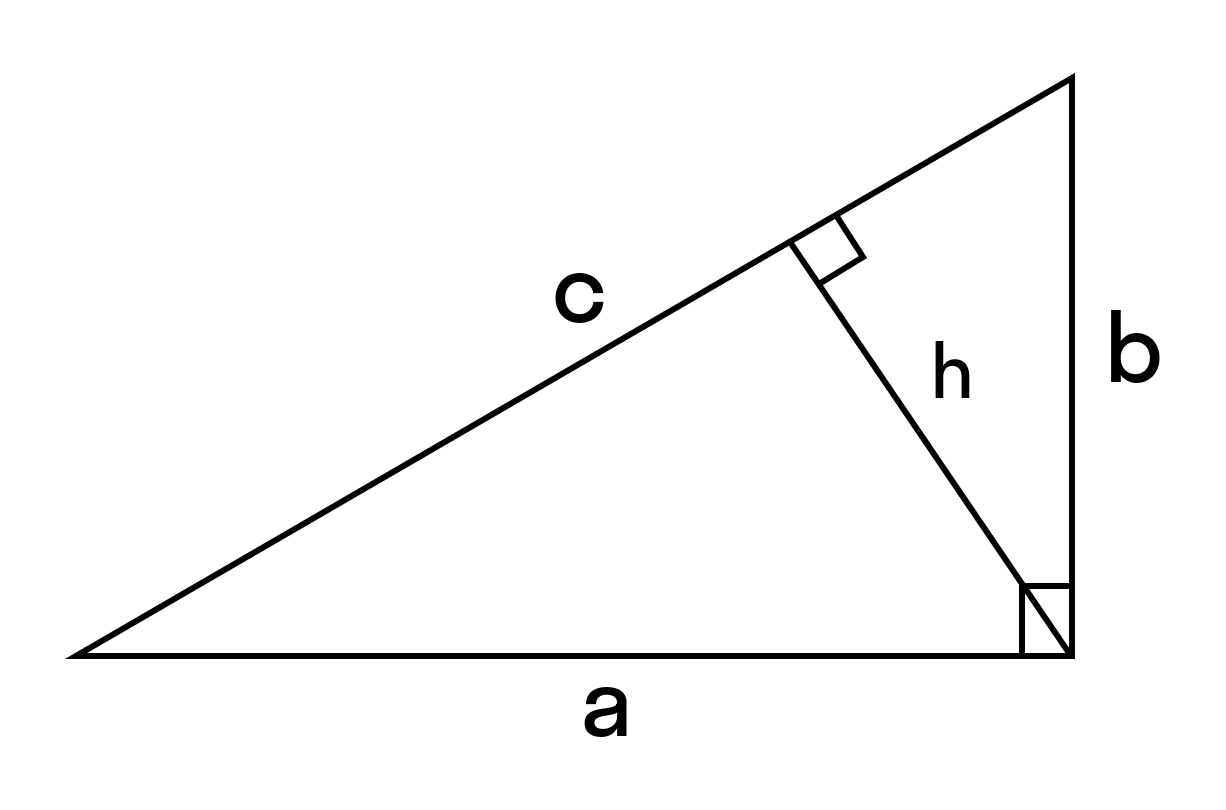
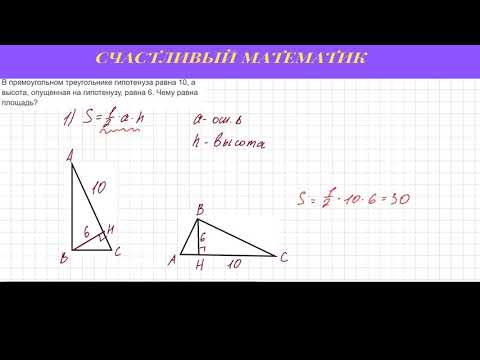
Формула для нахождения площади прямоугольного треугольника через гипотенузу
Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к гипотенузе.
где с — гипотенуза,
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через гипотенузу.
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Формула для нахождения площади прямоугольного треугольника через гипотенузу и острый угол
α, β — острые углы
Видео:Найти площадь треугольника АВС. Задачи по рисункамСкачать

Формулы нахождения площади прямоугольного треугольника через катет и угол
α, β — острые углы
Видео:8 класс, 14 урок, Площадь треугольникаСкачать

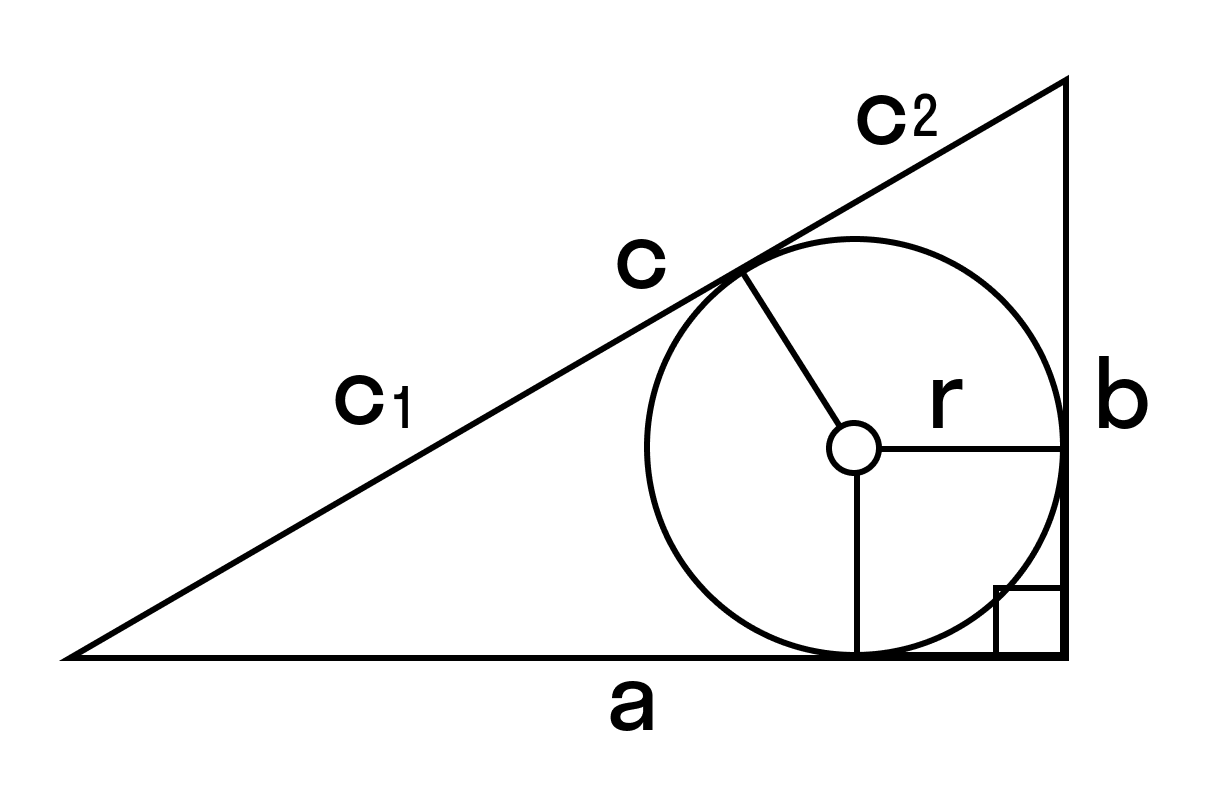
Формулы нахождения площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу
Радиус вписанной окружности выражается через катеты и гипотенузу по формуле:
S прямоугольного треугольника = r (r + c) = c1 × c2
r — радиус вписанной окружности
C1 и С2 — отрезки, полученные делением гипотенузы на две части точкой касания с окружностью
Уверены, что во всем разобрались? Закрепите знания на курсах обучения математике в онлайн-школе Skysmart!
Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Площадь прямоугольного треугольника через катеты — формула и примеры расчетов
Видео:Площадь прямоугольного треугольникаСкачать

Свойства треугольника
Пожалуй, в жизни любой человек сталкивается с треугольниками. Они бывают разными: остроугольными, тупоугольными, прямоугольными, равнобедренными и равносторонними. Но всех их объединяет один признак — существование трёх углов. Точное определение фигуре дали ещё в Древней Греции. Евклид утверждал, что этот объект состоит из трёх точек, расположенных на разных прямых, и трёх замкнутых линий, поочерёдно соединяющих эти точки.
Три точки, ограничивающие отрезки, называют вершинами, а линии, соединяющие их, — сторонами. Внутреннюю плоскость, заключённую в линии, называют площадью. Так как отрезки фигуры образуют три угла, то объект относится к классу многоугольников. Замкнутая прямая, соединяющая вершину с серединой противолежащей стороны, носит имя медиана. Всего их может быть три штуки, пересекаться они могут в одной точке, которую называют центроидом. Он является центром тяжести.
Если из угла провести перпендикуляр к противолежащей стороне, то полученная линия будет высотой. Линия, опущенная к стороне напротив угла и разделяющая его пополам, называется биссектрисой. В любой треугольник можно вписать окружность. Она будет единственной, так как должна касаться всех трёх сторон. Центр круга всегда будет совпадать с местом пересечения биссектрис.
Разделение треугольников происходит по размерам углов и сторон. Например, у равносторонней фигуры любой из трёх углов равен 60 градусам, у равнобедренной — две стороны и два угла равны. Для любого треугольника справедливо утверждать следующее:
- всегда напротив длинной стороны будет находиться больший угол;
- если две стороны равны, то напротив них будут равные углы;
- при сложении значений всех углов сумма составит 180 градусов;
- продолжив сторону за пределы объекта, можно получить внешний угол;
- одна из сторон всегда будет меньше суммы оставшихся и больше их разности.
В элементарной математике часто используют правила, называемые признаками подобия и равенства. Так, при сравнении две фигуры будут равными, если длины их сторон совпадают. Соответственно, углы тоже станут одинаковыми или будут равными две стороны и угол между ними.
Видео:Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Прямоугольная фигура
Треугольник с одним прямым углом, то есть составляющим 90 градусов, называется прямоугольным. Два отрезка, примыкающие к нему, называют катетами, а прямую, соединяющую их, — гипотенузой. Из любого треугольника можно получить две прямоугольных фигуры. Для этого нужно в нём опустить высоту. Многие свойства многоугольника идентичны прямоугольной фигуре. Два равных треугольника можно объединить в прямоугольник, при этом их гипотенузы будут совпадать с диагональю.
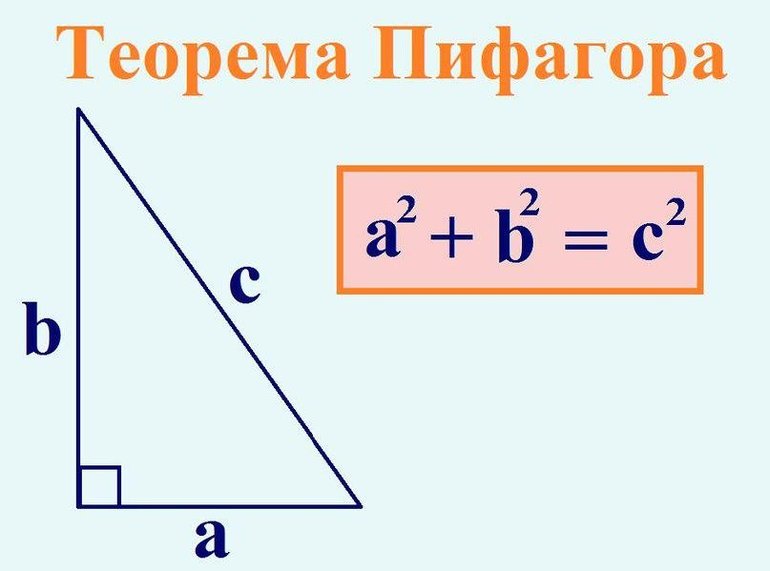
Основную особенность фигуры, которая позволяет посчитать площадь, подметил ещё Пифагор. Она очень простая и записывается как с 2 = а 2 + b 2 . В соответствии с этим правилом квадрат гипотенузы равняется результату сложения квадратов катетов, то есть сумма площадей квадратов, достроенных на катетах, совпадает с площадью квадрата, построенного на гипотенузе. Кроме основного свойства, чтобы найти площадь прямоугольного треугольника, нужно знать следующие правила:
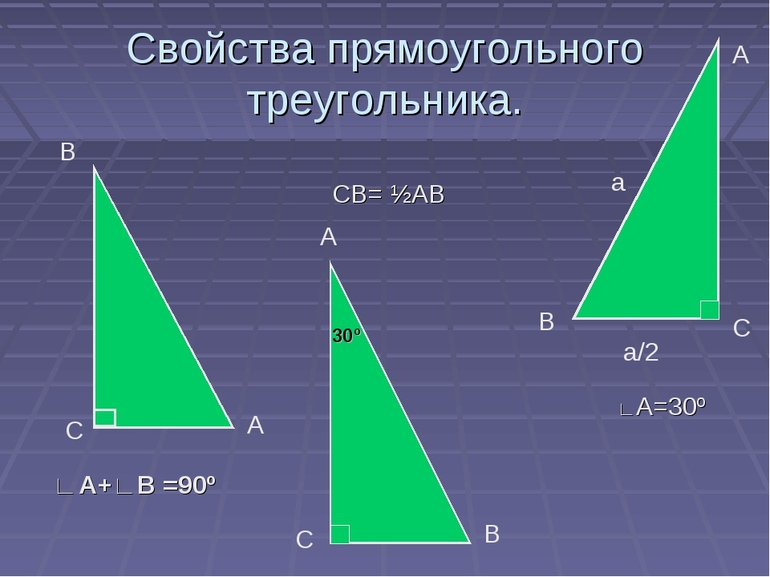
- при сложении двух острых углов сумма будет равняться 90 градусов;
- гипотенуза у фигуры всегда будет больше катета;
- длину катета, расположенного напротив угла в 30 градусов, можно найти, разделив гипотенузу пополам;
- катеты в прямоугольном треугольнике одновременно являются его высотами;
- величина радиуса описанной окружности совпадает с медианой.
Из теоремы Пифагора можно сделать важное следствие. Становится очевидным, что высота, опущенная из прямого угла, разделит гипотенузу на два отрезка: c1 = a2/c и c1 = b2/c. Полученные замкнутые линии являются проекциями катетов. В то же время высоту фигуры можно определить, используя следующую формулу: h = √ca + cb.
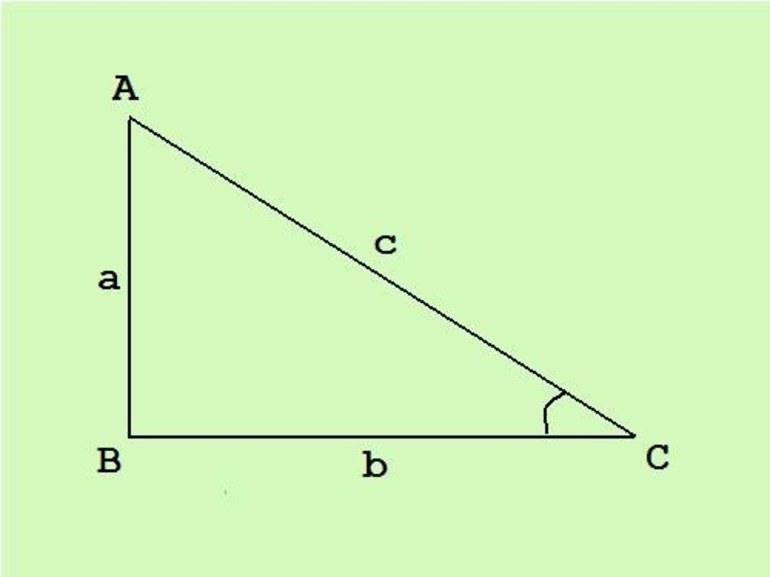
Если угол, располагающийся напротив катета a, обозначить альфой, а напротив b — бетой, то справедливо утверждать, что гипотенуза будет равняться: c = b /sin b = a / sin a = b / cos a = a / cos b = h = √a 2 + b 2 . Другими словами, длины катетов можно вычислить, используя синус противолежащего угла или косинус прилежащего. То есть получатся равенства: a = c * sin a = c * cos b и b = c * cos a = c * sin b. Учитывая тригонометрические правила, катеты можно найти, используя тангенс. Так, сторона b = a * tg b, катет a = b * tg a.
Все рассмотренные формулы и свойства помогают при нахождении площади фигуры. Но кроме них полезно знать и то, что радиус вписанной окружности в прямоугольную фигуру можно узнать, найдя разницу суммы катетов и гипотенузы, разделённую на 2, то есть r = (a + b — c) / 2.
Видео:Задача, которую исключили из экзамена в АмерикеСкачать

Формулы площади
Найти площадь треугольника с прямым углом можно различными способами. Но проще всего это сделать через катеты. Выражение для нахождения параметра довольно простое: S = (a * b) / 2. Это классическая формула площади прямоугольного треугольника. Существуют и другие формулы:
- S = (a 2 * tg b) / 2;
- S = (a 2 * ctg a) / 2;
- S = (b 2 * tg a) / 2;
- S = (b 2 * ctg b) / 2.
Другими словами, площадь можно определить, зная значения двух катетов, длину одного из них и разворот противолежащего или прилежащего угла. Для доказательства теоремы нахождения площади понадобится изобразить фигуры с катетами b и a. Фигуру можно достроить до параллелограмма, отложив параллельные катетам прямые. Вершины полученного объекта можно обозначить буквами A, B, C, D, начиная с прямого угла треугольника и двигаясь влево.
Прямоугольник образуется двумя треугольниками, равными между собой по трём сторонам: AB = CD, AC = BD (ВС — общая сторона). Учитывая равенства, можно утверждать, что площади фигур равны друг другу. Следовательно, площадь параллелограмма можно найти через сумму площадей двух треугольников: S = Sabc + Sacd. Отсюда верным будет утверждение, что площадь начального треугольника ABC равняется половине замкнутой области прямоугольника, а та соответствует произведению сторон: S = a * b, то есть AB * BC.
Эта формула легко доказывается с учётом того, что прямоугольник является фигурой, в которую можно вписать несколько четырёхугольников. Так как общая площадь будет равняться сумме площадей внутренних фигур, то верным будет равенство: (a + b)2 = S + S + a2 + b2 = a2 + 2ab + b2 = 2S + a2 + b2. Отсюда получим, что S = a* b. Следовательно, так как площадь треугольника равняется половине площади прямоугольной фигуры, то можно утверждать, что S = (a * b)/2 = (AB * BC) / 2. Формула доказана.
Из этого правила вытекают два следствия:
- площадь равняется половине результата перемножения катетов;
- когда высоты двух треугольных фигур совпадают, их площади можно соотнести как основания.
- если угол одного треугольника равен углу другого, то площади объектов соотносятся как результат умножения сторон с одинаковыми углами.
Использование рассмотренных следствий помогает при решении многих геометрических задач. Они касаются не только треугольников, но и других многоугольных фигур.
Видео:Как найти площадь треугольника без формулы?Скачать

Решение задач
Важно не только знать формулы для нахождения площади, но и уметь их применять на практике. Это возможно лишь с опытом, который можно получить, решая различные задания. Существуют определённые задачи, которые ученикам нужно решить самостоятельно. После успешного решения можно утверждать, что учащиеся полностью разобрались в теме, поэтому они могут переходить к следующему разделу геометрии. Вот некоторые задания, позволяющие закрепить теоретический материал:
- В прямоугольнике одна из сторон равна 35 см, а другая — 50 см. Нужно найти площадь фигур, полученных в результате проведения диагонали. В соответствии с правилом диагональ прямоугольника разделяет его на два равных прямоугольных треугольника, при этом его стороны являются катетами полученных фигур. Отсюда следует, что S1 = S2 = a * b / 2 = 35 * 50 / 2 = 1750 / 2 = 875 см².
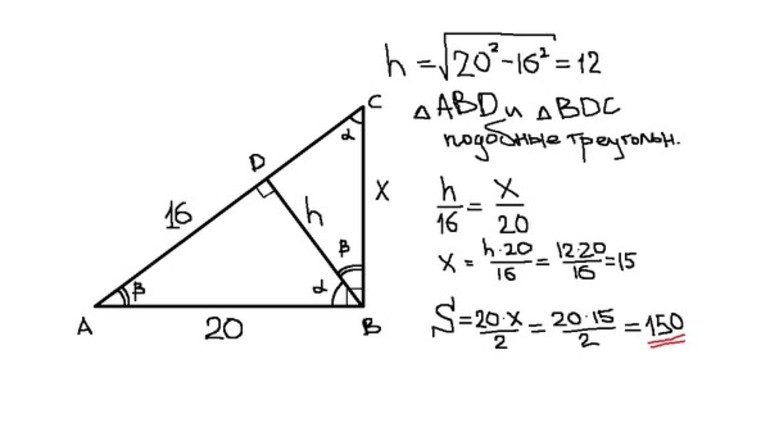
- Есть прямоугольный треугольник, катет которого равняется 15 см, а гипотенуза — 25 см. Нужно вычислить площадь фигуры. Для решения задачи следует узнать длину второго катета. Сделать это удастся, используя формулу гипотенузы: c = √a2 + b2. Из неё можно выразить неизвестный катет. Его длина будет равняться: b = √c2 — a2 = √252 — 152 = √625 — 225 = √400 = 20 см. Известные данные нужно подставить в формулу площади и выполнить расчёт: S = 20 * 15 / 2 = 150 см².
Длина катета в треугольнике равна 2 * √3 см, а противолежащий ему угол составляет 50 градусов. Необходимо вычислить площадь фигуры. Известно, что сумма углов в таком треугольнике — 180 градусов. Следовательно, разворот прилежащего к катету углу равняется a = 180 — 90 — b = 180 — 90 — 60 = 30 градусов. Теперь можно использовать формулу для нахождения площади прямоугольного многоугольника через катет и тангенс угла: S = (b 2 * tg a) / 2 = ((2 * √3) 2 * tg 30) / 2 = (12/2) * (√3/3) = 2√3 см 2 .
Таким образом, площадь прямоугольной фигуры — ее численная характеристика. Определить ее можно, используя несколько способов. При этом всегда необходимо знать длину хотя бы одного из катетов. Это связанно с тем, что две из трёх высот совпадают с ним.
🔍 Видео
🔴 Найдите площадь прямоугольного треугольника ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Найдите площадь прямоугольного треугольника ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Задача #22 Найдите площадь прямоугольного треугольника.Скачать
4 класс, 25 урок, Площадь прямоугольного треугольникаСкачать

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Площадь прямоугольного треугольника равна 200√3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать