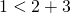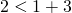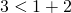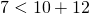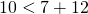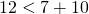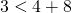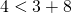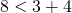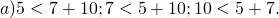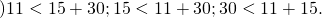Каким не может быть треугольник

Определение

Существующие треугольники — это такие треугольники,
существование которых можно доказать с помощью неравенств.

Например существование треугольника, изображенного на рисунке 1,
можно доказать с помощью неравенств: AB + BC > AC, AC + BC > AB, AB + AC > BC
Если эти три неравенства истинны значит треугольник существует,
иначе он не существует.

Также существование того или иного треугольника можно проверить с
помощью одного условия: Если большая сторона треугольника меньше
суммы двух других сторон, значит треугольник существует,
иначе он не существует.

Теорема

Для доказательства того, о чем мы говорили существует теорема под названием неравенство треугольника. Формулировка теоремы:
каждая сторона треугольника меньше суммы двух других сторон.

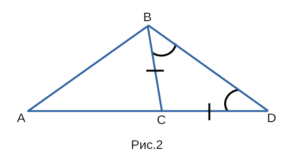
Докажем, что каждая сторона треугольника, изображенного на рисунке 2, меньше суммы двух других сторон:

Доказательство теоремы

1. Проведем отрезок CD равный отрезку CB.
2. △BCD — равнобедренный, значит ∠ CBD=∠CDB.
3. Рассмотрим △ABD: ∠ ABD >∠ CBD, следовательно ∠ ABD >∠ CDB, то AB

Видео:Треугольник Карпмана: как выйти?Скачать

Какими могут быть стороны треугольника

Какими могут быть стороны треугольника? Могут ли стороны треугольника быть равными данным числам? Существует ли треугольник со сторонами той или иной длины? . Рассмотрим конкретные задачи.

1) Существует ли треугольник со сторонами

а) 1 см, 2 см, 3 см;

б) 7 см, 10 см, 12 см?

Согласно неравенству треугольника, длина любой стороны треугольника меньше суммы длин двух других сторон. Проверяем, выполнено ли это условие для каждого отрезка. Для задачи а):

Третье неравенство неверно, следовательно, треугольника со сторонами 1 см, 2 см и 3 см не существует.

Все три условия выполнены, значит, треугольник со сторонами 7 см, 10 см и 12 см существует.

2) Можно ли построить треугольник со сторонами 3 см, 4 см, 8 см?

Проверяем, выполняется ли неравенство треугольника для каждого из отрезков:

Последнее неравенство не выполнено, поэтому треугольник со сторонами 3 см, 4 см и 8 см построить нельзя.

3) Какими могут быть стороны треугольника:

б) 11 дм, 15 дм, 30 дм?

Проверяем выполнение неравенства треугольника для каждой тройки отрезков:

Все три неравенства верны, следовательно, стороны треугольника могут быть равными 5 м, 7 м и10 м.

Третье неравенство не является верным, значит, стороны треугольника не могут быть равными 11 дм, 15 дм и 30 дм.

Видео:Как не попадать в треугольник Карпмана. Комплекс спасателя. Как перестать спасать других.Скачать

Треугольник — определение и основные свойства и виды треугольника

Что такое треугольник знают дети уже в самом младшем возрасте, они умеют находить треугольник среди множества геометрических фигур. Но вот уже в школе по геометрии проходят треугольник и надо не просто узнавать треугольник, но и дать определение этому понятию.

Видео:Что такое Треугольник Карпмана?Скачать

Определение треугольника

Треугольник — это геометрическая фигура, окруженная тремя отрезками прямой (конечные точки каждых двух смежных отрезков соединены или перекрываются), называется треугольником. Точки пересечения отрезков называются вершинами треугольника, а сами отрезки между двумя соседними вершинами треугольника называются сторонами треугольника.

Посмотрите на треугольник на рисунке.

У него три вершины — , , и три стороны , и . У каждого треугольника есть имя — это имя образовано вершинами треугольника. Наш треугольник зовут ([а-бэ-цэ]). А треугольник на вот этом рисунке

будут звать ([эм-эн-ка]).

По правилам математической грамотности треугольник, как и любой другой многоугольник, следует называть, начиная с левого нижнего угла и называя все вершины по часовой стрелке.

В треугольнике можно провести особенные стороны — высоту, медиану и биссектрису. Начнем с высоты треугольника.

Видео:Треугольник Карпмана. Треугольник Вашей судьбы. Ковалев С.В.Скачать

Высота треугольника

В каждом треугольнике можно провести три высоты. Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противолежащую этой вершине сторону.

Например, в треугольнике , высотой будет отрезок .

А теперь проведем из каждой вершины по высоте — получим три высоты — больше провести высот нельзя.

В этом треугольнике три высоты , , .

Про биссектрисы и медианы поговорим в других статьях. Сейчас же давайте с вами рассмотрим каким бывает треугольник.

Видео:ТРЕУГОЛЬНИК КАРПМАНА | ОНА | КАК ПЕРЕСТАТЬ БЫТЬ ЖЕРТВОЙСкачать

Виды треугольника

Виды треугольника могут быть по углам и по сторонам. То есть в первом случае вид треугольника зависит от того, какие в этом треугольнике углы, а во втором случае — какие в этом треугольнике стороны.

Виды треугольников по углам

В зависимости от того, все ли углы в треугольнике острые или есть тупой угол или угол, равный , треугольник бывает остроугольным, тупоугольным или прямоугольным.

Посмотрите на рисунки — перед вами три основных вида треугольника:

Виды треугольников по сторонам

Если у треугольника все стороны равны, то такой треугольник называют равносторонним или правильным. Если у треугольника равны только две стороны, то такой треугольник называют равнобедренным.

На рисунке показаны равносторонний и равнобедренный треугольники.

Видео:Что скрывает фрактальный треугольник? // Vital MathСкачать

Свойства сторон треугольника

Треугольник имеет важные свойства и характеристики.

Устойчивость — это важное свойство треугольника, оно вам еще пригодится в курсе физики. Но вначале мы с ним знакомимся на уроках геометрии.

Треугольник устойчив на любой своей стороне — то есть чтобы вывести его из состояния равновесия надо приложить силу.

Свойства сторон: разница между любыми двумя сторонами треугольника меньше, чем третья сторона, а также любая сторона треугольника меньше, чем сумма двух других сторон. То есть:

Например, пусть наш треугольник имеет длины двух сторон , а см. В каком диапазоне будет размер третьей стороны треугольника?

Решение: согласно свойству сторон треугольника, получим:

Таким образом, третья сторона треугольника может быть в диапазоне от 4 до 10 см. Или в целых числах ее длина может быть 5, 6, 7, 8 или 9 см.

Правило существования треугольника

Используя свойство сторон треугольника мы можем определить существует ли треугольник с определенными сторонами.

Для проверки сложите длины самых коротких сторон и если сумма их больше длины самой большой стороны, тогда треугольник существует.

Например, существует ли треугольник с длинами сторон 3, 7 и 15 см?

Решение: проверим по свойству сторон треугольника: складываем две самые короткие стороны 3 и 7 см: 3+7=10, а 10 7 — треугольник с такими длинами сторон существует.

Видео:Треугольник Карпмана - Михаил ЛабковскийСкачать

Свойство углов в треугольнике

Сумма всех углов в треугольнике равна .

Согласно этому свойству мы всегда можем, зная два угла в треугольнике, найти его третий угол. В прямоугольном треугольнике сумма двух острых углов всегда равна .

Например, пусть известно, что в треугольнике , , , нужно найти .

Так как сумма углов в треугольнике равна , то находим:

.

Ответ: .

Видео:Жертва, спасатель, преследователь: как работает треугольник Карпмана / Александр Шахов // Не ФрейдСкачать

Элементы композиции

Многие школьники спрашивают — а зачем нам знать про треугольник, как это может пригодиться в обычной жизни? Треугольник — простая фигура из которой можно составить более сложные. Это используется во многих сферах жизни, например, вы можете эргономично убирать в своей комнате, или красиво выкладывать бутерброды. Например, из двух равных треугольников можно составить параллелограмм.

А из двух равных прямоугольных треугольником — прямоугольник или квадрат. Два треугольника могут образовать трапецию, так как на рисунке. А вот какую фигурку можно смоделировать для программируемой игры — она вся сделана из треугольников:

Мы, рассмотрели самые важные свойства треугольника, и в дальнейшем изучим еще больше разных интересных свойств, закономерностей. Несмотря на свою простоту, треугольник таит в себе много загадок и открытий.

📹 Видео

Каким нужно быть, чтобы тебя не бросили? | Андрей Курпатов | Красная таблетка ONLINEСкачать

Треугольник Карпмана: большое надувательство (он не Преследователь, а вы не Спасатель)Скачать

Любовный треугольник. Стоит ли уходить к любовнице? Психолог Сергей Насибян об изменах и конфликтахСкачать

Бегите от партнера, если он так себя ведетСкачать

О чем должна знать каждая любовница? / Почему становятся любовницами? Любовный треугольникСкачать

Лабковский Треугольник Карпмана Не надо лезть в чужую жизнь когда вас об этом не просятСкачать

2 ПРИЧИНЫ ЖЕНСКОЙ НЕВЕРНОСТИСкачать

Выживший летчик рассказал, что он увидел в Бермудском треугольникеСкачать

Мотивация на выход из Жертвы/ Как перестать быть Жертвой/ Советы психолога/ Треугольник КарпманаСкачать

Причины любовного треугольникаСкачать

Нечто космическое под Бермудским треугольником может раскрыть его тайныСкачать