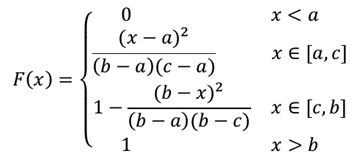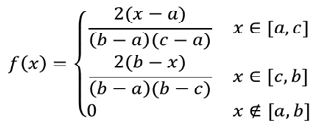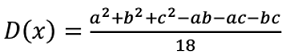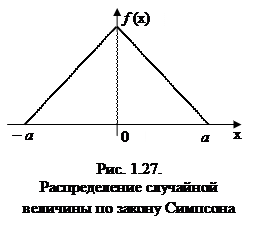
Закон распределения равнобедренного треугольника

К распределению по закону Симпсона приводит сложение двух случайных величин, подчиненных закону равной вероятности при одинаковых параметрах рассеяния. Кривая рассеяния имеет вид равнобедренного треугольника (рис. 1.27), из-за чего закон Симпсона часто называют законом треугольника.

При выборе в качестве начала отсчета случайной величины ее плотность распределения и математическое ожидание имеют следующий вид:

, (1.63)

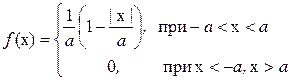
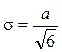
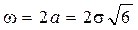
M_x = 0 , , . (1.64)

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: На стипендию можно купить что-нибудь, но не больше. 9137 – | 7300 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Функция треугольного распределения случайной величины определяется формулой:

Плотность треугольного распределения СВ находится по формуле:

Математическое ожидание — формула:

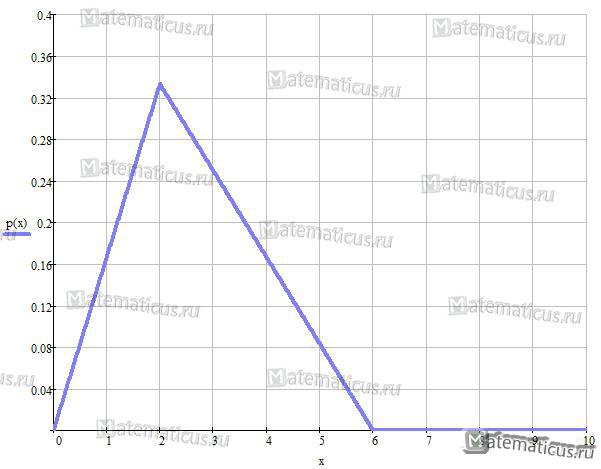
График плотности треугольного распределения случайной величины в диапазоне от -4 до 10

График плотности треугольного распределения случайной величины

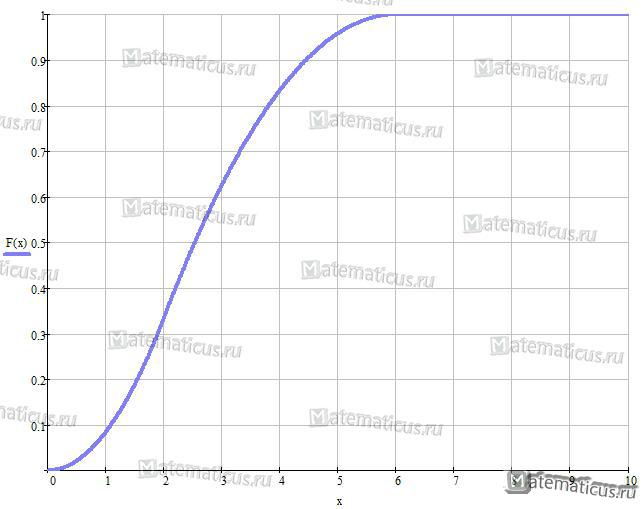
График функции треугольного распределения случайной величины

Треугольное распределения является приблизительной моделью и применяется, когда недостаточно данных или они отсутствуют. Треугольный закон распределения также используется для построения сложных законов распределения.

Он характерен для случайных погрешностей цифровых приборов, в которых измеряемая величина преобразуется в пропорциональный интервал времени Т_сч, называемый временем счета, а измерение этого интервала выполняется с помощью счетных импульсов стабильного генератора, имеющих период следования Т . В связи со случайным положением счетных импульсов относительно интервала Т_сч, а также случайным соотношением между периодом Т и временем счета Т_сч треугольный закон представляет собой композицию (объединение) двух равномерных законов с одинаковыми по величине максимальными погрешностями.

Функция распределения одномерной плотности вероятности случайных погрешностей для треугольного закона задается следующими соотношениями:

(46)где

График треугольного закона распределения приведен на рисунке 20.

Математическое ожидание величины x: определяется по той же формуле, что и равномерное:

Рисунок 20 – Треугольное распределение случайной величины

Среднее квадратическое отклонение определяется по формуле:

Теория вероятностей (стр. 13 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

Определение. Начальным моментом k-го порядка (k = 0, 1, 2, …) распределения случайной величины Х (если он существует) называется действительное число ак, определяемое формулой:

. (5.11)

ния случайной величины Х (если он существует) называется действительное число , определяемое по формуле:

. (5.12)

Из определения моментов следует, что

, , , , .

Отметим еще две важные характеристики распределения, связанные с моментами высшего порядка: (коэффициент асимметрии или «скошенности» распределения), (коэффициент эксцесса, (просто «эксцесс») или “островершинности” распределения).

Пример 1. Случайная величина Х подчинена закону распределения Парето с параметрами , , если ее функция распределения вероятностей имеет вид:

Найти основные характеристики , , Mo, Mе распределения Парето, выразив их через параметры распределения.

Решение. Находим плотность распределения вероятностей:

Математическое ожидание вычислим по формуле (5.8):

, .

Найдем второй начальный момент:

, а > 2.

Для вычисления дисперсии используем формулу:

.

Так как плотность вероятности f(x) монотонно убывает при х >, то М0 =.

Медиану Ме находим, как корень уравнения , откуда .

Пример 2. Случайная величина Х распределена по закону рав­нобедренного треугольника в интервале (-а; а) (закон Симпсона), если она непрерывного типа и ее плотность распределения вероятностей имеет вид, изображенный на рис. 14.

Написать выражение для f(x), вычислить функцию распределе­ния вероятностей, математическое ожидание, дисперсию, моду, ме­диану, эксцесс.

f(x)

1/a

Найдем плотность вероятностей, используя уравнение прямой в отрезках: f(x) = 0, если ха; или , если а a.

0, если

F(x) =

1, если = 0 и функция f(x) на интервале (-а; а) четна, а вне этого интервала равна нулю, то

Поступая аналогично и используя формулу (5.12), вычислим центральный момент четвертого порядка:

,

5.4. Примеры некоторых классических распределений

1. Закон равномерной плотности

В некоторых задачах практики встречаются непрерывные вели­чины, которые в пределах некоторого конечного интервала имеют постоянную плотность вероятностей. О таких случайных величинах говорят, что они распределяются по закону равномерной плотности.

Пример 1. Производится взвешивание тела на точных весах, но в распоряжении взвешивающего имеются только разновески весом не менее 1 г; результат взвешивания показывает, что вес тела заключен между а и (а + 1) граммами. Вес тела принят равным (а + 0,5) граммам. Допущенная при этом ошибка X, очевидно, есть случайная величи­на, распределенная c равномерной плотностью на интервале (-0,5; 0,5) г.

Пример 2. Пригородные поезда идут с интервалом 10 минут. Пассажир выходит на платформу в случайный момент времени. Время Т, в течение которого ему придется ждать поезда, представля­ет собой случайную величину, распределенную с равномерной плот­ностью на интервале (0; 10) минут.

Рассмотрим случайную величину X, подчиненную закону рав­номерной плотности на интервале от а до b, и напишем для нее выражение плотности распределения f(x).

Так как

а площадь, ограниченная графиком f(x) и осью абсцисс, равна еди­нице: с(b — а) = 1, то

и плотность распределения f(x) имеет вид:

(5.13)

Напишем выражение для функции распределения F(x), исполь­зуя формулу (5.6):

(5.14)

График функции F(x) приведен на рис. 15.

Определим числовые характеристики случайной величины X, имеющей равномерное распределение на интервале от а до b. Мате­матическое ожидание величины Х равно: .

В силу симметрии равномерного распределения медиана величины Х также равна Ме =.

Моды закон равномерной плотности не имеет.

По формуле (5.10) находим дисперсию X:

откуда среднее квадратическое отклонение

.

В силу симметрии распределения его асимметрия равна нулю:

F(x)

1

Для определения эксцесса находим четвертый центральный мо­мент:

, отсюда

.

Функцию R(t) называют функцией надежности (она определяет вероятность безотказной работы элемента за время t).

Часто функция F(t) имеет показательное распределение, функ­ция распределения которого F(t)=1— .

Следовательно, функция надежности R(t) имеет вид:

Показательным законом надежности называют функцию надеж­ности R(t), определяемую равенством

где – интенсивность отказов.

Пример 1. Непрерывная случайная величина Х распределена по показательному закону f(x) = 5 (х 0). Найти математическое ожидание, среднее квадратическое отклонение и дисперсию X.

Решение. Так как М(Х) и a(Х) показательного распределения равны между собой и равны числу 1/ – параметру показательного распределения, то . Дисперсия D(X) = (0,2)2 = 0,04.

Пример 2. Время безотказной работы элемента, распределенного по показательному закону f(x) = 0,05е-0,05t (t > 0), где t – время в сутках. Найти вероятность того, что элемент проработает 20 суток.

Решение. По условию постоянная интенсивность отказов = 0,05. Далее по формуле (5.16) определим искомую вероятность R(20) = e-0,05*20 = e-10,37.

1. Распределение Вейбулла

Случайная величина Х непрерывного типа подчиняется закону распределения Вейбулла с параметрами a R, b > 0, если ее плотность распределения вероятностей записывается в виде

Распределение Вейбулла в ряде случаев характеризует срок службы радиоэлектронной аппаратуры и, кроме того, применяется для аппроксимации различных несимметричных распределений в математической статистике. Легко заметить то, что показательное распределение – частный случай распределения Вейбулла (n = 1, а = 0, b = 1/ ).

Вычислим математическое ожидание случайной величины X, имеющей распределение Вейбулла.

Сделаем подстановку , отсюда , , нижний предел интегрирования по переменной t равен 0, а верхний равен

и, следовательно,

Первый из полученных интегралов равен 1, а второй

где – гамма-функция Эйлера. Итак,

.

Непрерывная случайная величина Х имеет гамма-распределение с параметрами, а > 0 и b > 0, если ее плотность вероятностей имеет сле­дующий вид:

Показательное распределение с параметром также является частным случаем гамма-распределения (а = 1, b =).

Другой частный случай гамма-распределения с параметрами

(n – натуральное число ), называется распределением Хи-квадрат с n степенями свободы (пишут X2(n)). Распределение Х2(n) играет большую роль в математической статистике.

Если случайная величина Х подчинена закону Х2(n), то ее плот­ность вероятностей записывается в виде

Треугольное распределение

Функция треугольного распределения случайной величины определяется формулой:

Плотность треугольного распределения СВ находится по формуле:

Математическое ожидание — формула:

График плотности треугольного распределения случайной величины в диапазоне от -4 до 10

График плотности треугольного распределения случайной величины

График функции треугольного распределения случайной величины

Треугольное распределения является приблизительной моделью и применяется, когда недостаточно данных или они отсутствуют. Треугольный закон распределения также используется для построения сложных законов распределения.

💡 Видео