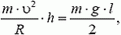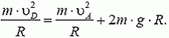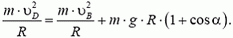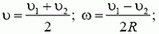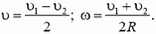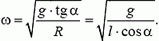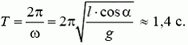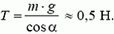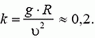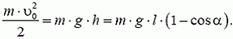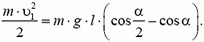Какие силы действуют на автомобиль при движении по окружности

Асламазов Л.Г. Движение по окружности // Квант. — 1972. — № 9. — С. 51-57.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

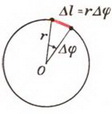
Для описания движения по окружности наряду с линейной скоростью вводят понятие угловой скорости. Если точка при движении по окружности за время Δt описывает дугу, угловая мера которой Δφ, то угловая скорость .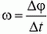

Угловая скорость ω связана с линейной скоростью υ соотношением υ = ω·r, где r — радиус окружности, по которой движется точка (рис. 1). Понятие угловой скорости особенно удобно для описания вращения твердого тела вокруг оси. Хотя линейные скорости у точек, находящихся на разном расстоянии от оси, будут неодинаковыми, их угловые скорости будут равны, и можно говорить об угловой скорости вращения тела в целом.

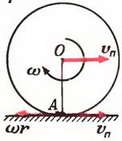
Задача 1. Диск радиуса r катится без проскальзывания по горизонтальной плоскости. Скорость центра диска постоянная и равна υ_п. С какой угловой скоростью при этом вращается диск?

Каждая точка диска участвует в двух движениях — в поступательном движении со скоростью υ_п вместе с центром диска и во вращательном движении вокруг центра с некоторой угловой скоростью ω.

Для нахождения ω воспользуемся отсутствием проскальзывания, то есть тем, что в каждый момент времени скорость точки диска, соприкасающейся с плоскостью, равна нулю. Это означает, что для точки А (рис. 2) скорость поступательного движения υ_п равна по величине и противоположна по направлению линейной скорости вращательного движения υ_вр = ω·r. Отсюда сразу получаем .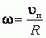

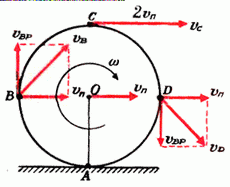
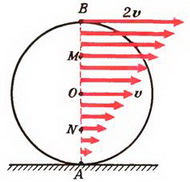
Задача 2. Найти скорости точек В, С и D того же диска (рис. 3).

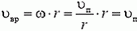
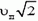
Рассмотрим вначале точку В. Линейная скорость ее вращательного движения направлена вертикально вверх и равна , то есть по величине равна скорости поступательного движения, которая, однако, направлена горизонтально. Складывая векторно эти две скорости, находим, что результирующая скорость υ_B по величине равна и образует угол 45º с горизонтом. У точки С скорости вращательного и поступательного движения направлены в одну сторону. Результирующая скорость υ_C равна 2υ_п и направлена горизонтально. Аналогично находится и скорость точки D (см. рис. 3).

Даже в том случае, когда скорость точки, движущейся по окружности, не меняется по величине, точка имеет некоторое ускорение, так как меняется направление вектора скорости. Это ускорение называется центростремительным. Оно направлено к центру окружности и равно 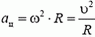(R — радиус окружности, ω и υ — угловая и линейная скорости точки).

Если же скорость точки, движущейся по окружности, меняется не только по направлению, но и по величине, то наряду с центростремительным ускорением существует и так называемое тангенциальное ускорение. Оно направлено по касательной к окружности и равно отношению 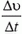(Δυ — изменение величины скорости за время Δt).

Задача 3. Найти ускорения точек А, В, С и D диска радиуса r, катящегося без проскальзывания по горизонтальной плоскости. Скорость центра диска постоянна и равна υ_п (рис. 3).

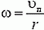
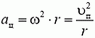
В системе координат, связанной с центром диска, диск вращается с угловой скоростью ω, а плоскость движется поступательно со скоростью υ_п. Проскальзывание между диском и плоскостью отсутствует, следовательно, . Скорость поступательного движения υ_п не меняется, поэтому угловая скорость вращения диска постоянная и точки диска имеют только центростремительное ускорение , направленное к центру диска. Так как система координат движется без ускорения (с постоянной скоростью υ_п), то в неподвижной системе координат ускорения точек диска будут теми же.

Перейдем теперь к задачам на динамику вращательного движения. Вначале рассмотрим простейший случай, когда движение по окружности происходит с постоянной скоростью. Так как ускорение тела при этом направлено к центру, то и векторная сумма всех сил, приложенных к телу, должна быть тоже направлена к центру, и по II закону Ньютона .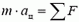

Следует помнить, что в правую часть этого уравнения входят только реальные силы, действующие на данное тело со стороны других тел. Никакой центростремительной силы при движении по окружности не возникает. Этим термином пользуются просто для обозначения равнодействующей сил, приложенных к телу, движущемуся по окружности. Что касается центробежной силы, то она возникает только при описании движения по окружности в неинерциальной (вращающейся) системе координат. Мы пользоваться здесь понятием центростремительной и центробежной силы вообще не будем.

Задача 4. Определить наименьший радиус закругления дороги, которое автомобиль может пройти при скорости υ = 70 км/ч и коэффициенте трения шин о дорогу k =0,3.

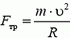
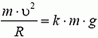
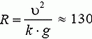
На автомобиль действуют сила тяжести Р = m·g, сила реакции дороги N и сила трения F_тp между шинами автомобиля и дорогой. Силы Р и N направлены вертикально и равны по величине: P = N. Сила трения, препятствующая проскальзыванию («заносу») автомобиля, направлена к центру поворота и сообщает центростремительное ускорение: . Максимальное значение силы трения F_{тр max} = k·N = k·m·g, поэтому минимальное значение радиуса окружности, по которой еще возможно движение со скоростью υ, определяется из уравнения . Отсюда (м).

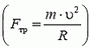
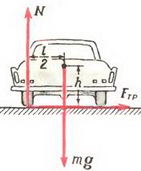
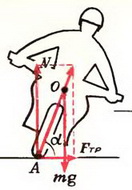
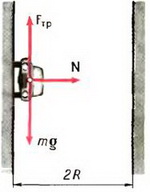
Сила реакции дороги N при движении автомобиля по окружности не проходит через центр тяжести автомобиля. Это связано с тем, что ее момент относительно центра тяжести должен компенсировать момент силы трения, стремящийся опрокинуть автомобиль. Величина силы трения тем больше, чем больше скорость автомобиля . При некотором значении скорости момент силы трения превысит момент силы реакции и автомобиль опрокинется.

Задача 5. При какой скорости автомобиль, движущийся по дуге окружности радиуса R = 130 м, может опрокинуться? Центр тяжести автомобиля находится на высоте h = 1 м над дорогой, ширина следа автомобиля l = 1,5 м (рис. 4).

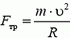
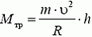
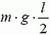
В момент опрокидывания автомобиля как сила реакции дороги N, так и сила трения F_тp приложены к «внешнему» колесу. При движении автомобиля по окружности со скоростью υ на него действует сила трения . Эта сила создает момент относительно центра тяжести автомобиля . Максимальный момент силы реакции дороги N = m·g относительно центра тяжести равен (в момент опрокидывания сила реакции проходит через внешнее колесо). Приравнивая эти моменты, найдем уравнение для максимальной скорости, при которой автомобиль еще не опрокинется:

Откуда 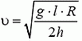≈ 30 м/с ≈ 110 км/ч.

Чтобы автомобиль мог двигаться с такой скоростью, необходим коэффициент трения 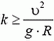(см. предыдущую задачу).

Аналогичная ситуация возникает при повороте мотоцикла или велосипеда. Сила трения, создающая центростремительное ускорение, имеет момент относительно центра тяжести, стремящийся опрокинуть мотоцикл. Поэтому для компенсации этого момента моментом силы реакции дороги мотоциклист наклоняется в сторону поворота (рис. 5).

Задача 6. Мотоциклист едет по горизонтальной дороге со скоростью υ = 70 км/ч, делая поворот радиусом R = 100 м. На какой угол α к горизонту он должен при этом наклониться, чтобы не упасть?

Сила трения между мотоциклом и дорогой 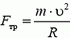, так как она сообщает мотоциклисту центростремительное ускорение. Сила реакции дороги N = m·g. Условие равенства моментов силы трения и силы реакции относительно центра тяжести дает уравнение: F_тp·l·sin α = N·l·cos α, где l — расстояние ОА от центра тяжести до следа мотоцикла (см. рис. 5).

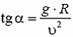
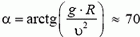
Подставляя сюда значения F_тp и N, находим что или . Отметим, что равнодействующая сил N и F_тp при этом угле наклона мотоцикла проходит через центр тяжести, что и обеспечивает равенство нулю суммарного момента сил N и F_тp.

Для того, чтобы увеличить скорость движения по закруглению дороги, участок дороги на повороте делают наклонным. При этом в создании центростремительного ускорения, кроме силы трения, участвует и сила реакции дороги.

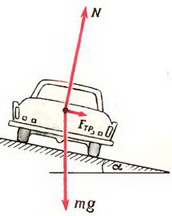
Задача 7. С какой максимальной скоростью υ может двигаться автомобиль по наклонному треку с углом наклона α при радиусе закругления R и коэффициенте трения шин о дорогу k?

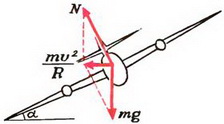
На автомобиль действуют сила тяжести m·g, сила реакции N, направленная перпендикулярно плоскости трека, и сила трения F_тp, направленная вдоль трека (рис. 6).

Так как нас не интересуют в данном случае моменты сил, действующих на автомобиль, мы нарисовали все силы приложенными к центру тяжести автомобиля. Векторная сумма всех сил должна быть направлена к центру окружности, по которой движется автомобиль, и сообщать ему центростремительное ускорение. Поэтому сумма проекций сил на направление к центру (горизонтальное направление) равна 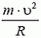, то есть

Сумма проекций всех сил на вертикальное направление равна нулю:

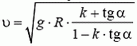
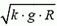
Подставляя в эти уравнения максимальное возможное значение силы трения F_тp = k·N и исключая силу N, находим максимальную скорость , с которой еще возможно движение по такому треку. Это выражение всегда больше значения , соответствующего горизонтальной дороге.

Разобравшись с динамикой поворота, перейдем к задачам на вращательное движение в вертикальной плоскости.

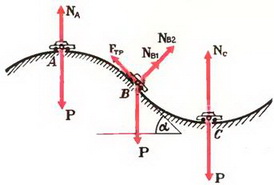
Задача 8. Автомобиль массы m = 1,5 т движется со скоростью υ = 70 км/ч по дороге, показанной на рисунке 7. Участки дороги АВ и ВС можно считать дугами окружностей радиуса R = 200 м, касающимися друг друга в точке В. Определить силу давления автомобиля на дорогу в точках А и С. Как меняется сила давления при прохождении автомобилем точки В?

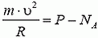
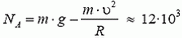
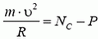
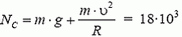
В точке А на автомобиль действуют сила тяжести Р = m·g и сила реакции дороги N_A. Векторная сумма этих сил должна быть направлена к центру окружности, то есть вертикально вниз, и создавать центростремительное ускорение: , откуда (Н). Сила давления автомобиля на дорогу равна по величине и противоположна по направлению силе реакции. В точке С векторная сумма сил направлена вертикально вверх: и (Н). Таким образом, в точке А сила давления меньше силы тяжести, а в точке С — больше.

В точке В автомобиль переходит с выпуклого участка дороги на вогнутый (или наоборот). При движении по выпуклому участку проекция силы тяжести на направление к центру должна превышать силу реакции дороги N_B1, причем 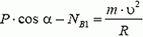. При движении по вогнутому участку дороги, наоборот, сила реакции дороги N_В2 превосходит проекцию силы тяжести: .

Из этих уравнений получаем, что при прохождении точки В сила давления автомобиля на дорогу меняется скачком на величину 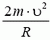≈ 6·10 3 Н. Разумеется, такие ударные нагрузки действуют разрушающе как на автомобиль, так и на дорогу. Поэтому дороги и мосты всегда стараются делать так, чтобы их кривизна менялась плавно.

При движении автомобиля по окружности с постоянной скоростью сумма проекций всех сил на направление, касательное к окружности, должна быть равна нулю. В нашем случае касательная составляющая силы тяжести уравновешивается силой трения между колесами автомобиля и дорогой.

Величина силы трения регулируется вращательным моментом, прикладываемым к колесам со стороны мотора. Этот момент стремится вызвать проскальзывание колес относительно дороги. Поэтому возникает сила трения, препятствующая проскальзыванию и пропорциональная приложенному моменту. Максимальное значение силы трения равно k·N, где k — коэффициент трения между шинами автомобиля и дорогой, N — сила давления на дорогу. При движении автомобиля вниз сила трения играет роль тормозящей силы, а при движении вверх, наоборот, роль силы тяги.

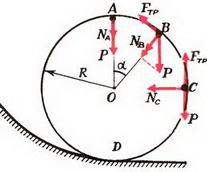
Задача 9. Автомобиль массой m = 0,5 т, движущийся со скоростью υ = 200 км/ч, совершает «мертвую петлю» радиуса R = 100 м (рис. 8). Определить силу давления автомобиля на дорогу в верхней точке петли А; в точке В, радиус-вектор которой составляет угол α = 30º с вертикалью; в точке С, в которой скорость автомобиля направлена вертикально. Возможно ли движение автомобиля по петле с такой постоянной скоростью при коэффициенте трения шин о дорогу k = 0,5?

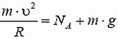
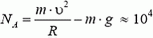
В верхней точке петли сила тяжести и сила реакции дороги N_A направлены вертикально вниз. Сумма этих сил создает центростремительное ускорение: . Поэтому Н.

Сила давления автомобиля на дорогу равна по величине и противоположна по направлению силе N_А.

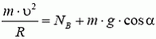
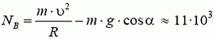
В точке В центростремительное ускорение создается суммой силы реакции и проекции силы тяжести на направление к центру: . Отсюда Н.

Легко видеть, что N_B > N_A; с увеличением угла α сила реакции дороги увеличивается.

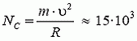
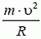
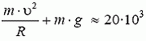
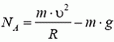
В точке С сила реакции Н; центростремительное ускорение в этой точке создается только силой реакции, а сила тяжести направлена по касательной. При движении по нижней части петли сила реакции будет превышать и максимальное значение Н сила реакции имеет в точке D. Значение , таким образом, является минимальным значением силы реакции.

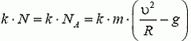
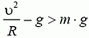
Скорость автомобиля будет постоянной, если касательная составляющая силы тяжести не превышает максимальной силы трения k·N во всех точках петли. Это условие заведомо выполняется, если минимальное значение превосходит максимальное значение касательной составляющей силы веса. В нашем случае это максимальное значение равно m·g (оно достигается в точке С), и условие выполняется при k = 0,5, υ = 200 км/ч, R = 100 м.

Таким образом, в нашем случае движение автомобиля по «мертвой петле» с постоянной скоростью возможно.

Рассмотрим теперь движение автомобиля по «мертвой петле» с выключенным мотором. Как уже отмечалось, обычно момент силы трения противодействует моменту, приложенному к колесам со стороны мотора. При движении автомобиля с выключенным мотором этого момента нет, и силой трения между колесами автомобиля и дорогой можно пренебречь.

Скорость автомобиля уже не будет постоянной — касательная составляющая силы тяжести замедляет или ускоряет движение автомобиля по «мертвой петле». Центростремительное ускорение тоже будет меняться. Создается оно, как обычно, равнодействующей силы реакции дороги и проекции силы тяжести на направление к центру петли.

Задача 10. Какую наименьшую скорость должен иметь автомобиль в нижней точке петли D (см. рис. 8) для того, чтобы совершить ее с выключенным мотором? Чему будет равна при этом сила давления автомобиля на дорогу в точке В? Радиус петли R = 100 м, масса автомобиля m = 0,5 т.

Посмотрим, какую минимальную скорость может иметь автомобиль в верхней точке петли А, чтобы продолжать двигаться по окружности?

Центростремительное ускорение в этой точке дороги создается суммой силы тяжести и силы реакции дороги . Чем меньшую скорость имеет автомобиль, тем меньшая возникает сила реакции N_A. При значении эта сила обращается в нуль. При меньшей скорости сила тяжести превысит значение, необходимое для создания центростремительного ускорения, и автомобиль оторвется от дороги. При скорости сила реакции дороги обращается в нуль только в верхней точке петли. В самом деле, скорость автомобиля на других участках петли будет большей, и как легко видеть из решения предыдущей задачи, сила реакции дороги 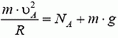тоже будет большей, чем в точке А. Поэтому, если автомобиль в верхней точке петли имеет скорость , то он нигде не оторвется от петли.

Теперь определим, какую скорость должен иметь автомобиль в нижней точке петли D, чтобы в верхней точке петли А его скорость . Для нахождения скорости υ_D можно воспользоваться законом сохранения энергии, как если бы автомобиль двигался только под действием силы тяжести. Дело в том, что сила реакции дороги в каждый момент направлена перпендикулярно перемещению автомобиля, а, следовательно, ее работа равна нулю (напомним, что работа ΔA = F·Δs·cos α, где α — угол между силой F и направлением перемещения Δs). Силой трения между колесами автомобиля и дорогой при движении с выключенным мотором можно пренебречь. Поэтому сумма потенциальной и кинетической энергии автомобиля при движении с выключенным мотором не меняется.

Приравняем значения энергии автомобиля в точках А и D. При этом будем отсчитывать высоту от уровня точки D, то есть потенциальную энергию автомобиля в этой точке будем считать равной нулю. Тогда получаем

Подставляя сюда значение для искомой скорости υ_D, находим: ≈ 70 м/с ≈ 260 км/ч.

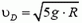
Если автомобиль въедет в петлю с такой скоростью, то он сможет совершить ее с выключенным мотором.

Определим теперь, с какой силой при этом автомобиль будет давить на дорогу в точке В. Скорость автомобиля в точке В опять легко находится из закона сохранения энергии:

Подставляя сюда значение 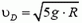, находим, что скорость .

Воспользовавшись решением предыдущей задачи, по заданной скорости находим силу давления в точке B:

Н.

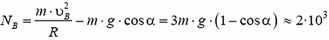
Аналогично можно найти силу давления в любой другой точке «мертвой петли».

1. Найти угловую скорость искусственного спутника Земли, вращающегося по круговой орбите с периодом обращения Т = 88 мин. Найти линейную скорость движения этого спутника, если известно, что его орбита расположена на расстоянии R = 200 км от поверхности Земли.

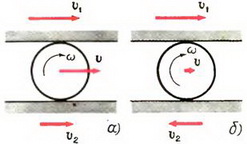
2. Диск радиуса R помещен между двумя параллельными рейками. Рейки движутся со скоростями υ₁ и υ₂. Определить угловую скорость вращения диска и скорость его центра. Проскальзывание отсутствует.

3. Диск катится по горизонтальной поверхности без проскальзывания. Показать, что концы векторов скоростей точек вертикального диаметра находятся на одной прямой.

4. Самолет движется по окружности с постоянной горизонтальной скоростью υ = 700 км/час. Определить радиус R этой окружности, если корпус самолета наклонен на угол α = 5°.

5. Груз массы m = 100 г, подвешенный на нити длины l = 1 м, равномерно вращается по кругу в горизонтальной плоскости. Найти период обращения груза, если при его вращении нить отклонена по вертикали на угол α = 30°. Определить также натяжение нити.

6. Автомобиль движется со скоростью υ = 80 км/ч по внутренней поверхности вертикального цилиндра радиуса R = 10 м по горизонтальному кругу. При каком минимальном коэффициенте трения между шинами автомобиля и поверхностью цилиндра это возможно?

7. Груз массой m подвешен на нерастяжимой нити, максимально возможное натяжение которой равно 1,5m·g. На какой максимальный угол α можно отклонить нить от вертикали, чтобы при дальнейшем движении груза нить не оборвалась? Чему будет равно при этом натяжение нити в тот момент, когда нить составит угол α/2 с вертикалью?

I. Угловая скорость искусственного спутника Земли 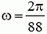≈ 0,071 рад/с. Линейная скорость спутника υ = ω·R. где R — радиус орбиты. Подставляя сюда R = R₃ + h, где R₃ ≈ 6400 км, находим υ ≈ 467 км/с.

2. Здесь возможны два случая (рис. 1). Если угловая скорость диска ω, а скорость его центра υ, то скорости точек, соприкасающихся с рейками, будут соответственно равны

(Мы приняли для определенности, что υ₁ > υ₂). Решая эти системы, находим:

а)

б)

3. Скорость любой точки М, лежащей на отрезке ОВ (см. рис. 2), находится по формуле υ_M = υ + ω·r_M, где r_M — расстояние от точки М до центра диска О. Для любой точки N, принадлежащей отрезку ОА, имеем: υ_N = υ – ω·r_N, где r_N — расстояние от точки N до центра. Обозначим через ρ расстояние от любой точки диаметра ВА до точки А соприкосновения диска с плоскостью. Тогда очевидно, что r_M = ρ – R и r_N = R – ρ = –(ρ – R). где R — радиус диска. Поэтому скорость любой точки на диаметре ВА находится по формуле: υ_ρ = υ + ω·(ρ – R). Так как диск катится без проскальзывания, то 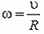и для скорости υ_ρ получаем υ_ρ = ω·ρ. Отсюда следует, что концы векторов скоростей находятся на прямой, выходящей из точки А и наклоненной к диаметру ВА под углом, пропорциональным угловой скорости вращения диска ω.

Доказанное утверждение позволяет нам сделать вывод, что сложное движение точек, находящихся на диаметре ВА, можно в каждый данный момент рассматривать как простое вращение вокруг неподвижной точки А с угловой скоростью ω, равной угловой скорости вращения вокруг центра диска. В самом деле, в каждый момент скорости этих точек направлены перпендикулярно диаметру ВА, а по величине равны произведению ω на расстояние до точки А.

Оказывается, что это утверждение справедливо для любой точки диска. Более того, оно является общим правилом. При любом движении твердого тела в каждый момент существует ось, вокруг которой тело просто вращается — мгновенная ось вращения.

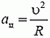
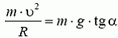
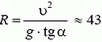
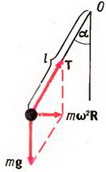
4. На самолет действуют (см. рис. 3) сила тяжести Р = m·g и подъемная сила N, направленная перпендикулярно плоскости крыльев (так как самолет движется с постоянной скоростью, то сила тяги и сила лобового сопротивления воздуха уравновешивают друг друга). Равнодействующая сил Р и N должна быть направлена к центру окружности, по которой движется самолет, и создавать центростремительное ускорение . Из рисунка находим:

или км.

5. Равнодействующая силы тяжести Р = m·g и силы натяжения нити Т должна создавать центростремительное ускорение а_ц = ω 2 ·R, где R = l·sin α — радиус круга, по которому вращается груз. Из рисунка 4 получаем:

m·ω 2 ·R = m·g·tg α, откуда

Период обращения груза

Натяжение нити

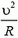
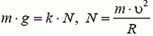
6. На автомобиль действуют (рис. 5) сила тяжести Р = m·g, сила реакции со стороны цилиндра N и сила трения F_тp. Так как автомобиль движется по горизонтальному кругу, то силы Р и F_тp уравновешивают друг друга, а сила N создает центростремительное ускорение . Максимальное значение силы трения связано с силой реакции N соотношением: F_тp = k·N. В результате получаем систему уравнений: , из которой находится минимальное значение коэффициента трения

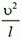
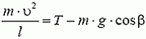
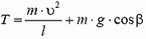
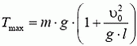
7. Груз будет двигаться по окружности радиуса l (рис. 6). Центростремительное ускорение груза (υ — скорость груза) создается разностью величин силы натяжения нити Т и проекции силы тяжести m·g направление нити: . Поэтому , где β — угол, образуемый нитью с вертикалью. По мере того, как груз будет опускаться, его скорость будет расти, а угол β будет уменьшаться. Натяжение нити станет максимальным при угле β = 0 (в тот момент, когда нить будет вертикальной): . Максимальная скорость груза υ₀ находится по углу α, на который отклоняют нить, из закона сохранения энергии:

Используя это соотношение, для максимального значения натяжения нити получаем формулу: T_max = m·g·(3 – 2 cos α). По условию задачи T_mах = 2m·g. Приравнивая эти выражения, находим cos α = 0,5 и, следовательно, α = 60°.

Определим теперь натяжение нити при 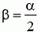. Скорость груза в этот момент также находится из закона сохранения энергии:

Подставляя значение υ₁ в формулу для силы натяжения, находим:

Видео:Силы действующие на автомобиль при движении Подробный видеоурокСкачать

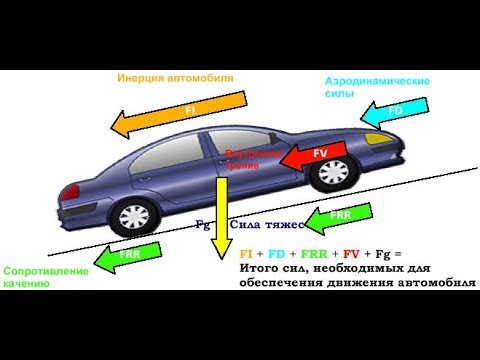
Силы действующие на автомобиль при движении

Видео:Физика - движение по окружностиСкачать

Схема сил действующих на ведущее колесо

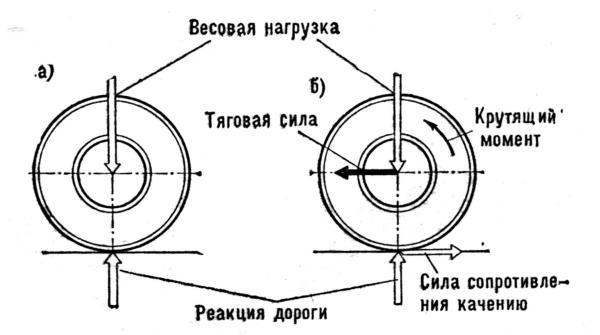
На движущийся автомобиль действует ряд сил, часть из которых направлена по оси движения автомобиля, а часть — под углом к этой оси. Условимся называть первые из этих сил продольными, а вторые боковыми.

Рис. Схема сил действующих на ведущее колесо.
а — состояние неподвижности; б — состояние движения

Продольные силы могут быть направлены как по ходу, так и против хода движения автомобиля. Силы, направленные по ходу движения, являются движущимися и стремятся продолжить движение. Силы, направленные против хода движения, являются силами сопротивления и стремятся остановить автомобиль.

На автомобиль, движущийся по горизонтальному и прямому участку дороги, действуют следующие продольные силы:

• тяговая сила
• сила сопротивления воздуха
• сила сопротивления качению

При движении автомобиля в гору возникает сила сопротивления подъему, а при разгоне автомобиля—сила сопро­тивления разгону (сила инерции).

Видео:Центробежная сила! Это Должен Знать Каждый Водитель [Автошкола RED]Скачать

Тяговая сила

Развиваемый двигателем автомобиля крутящий момент передается на ведущие колеса. В передаче крутящего момента от двигателя к ведущим колесам участвуют механизмы трансмиссии. Крутящий момент на ведущих колесах зависит от крутящего момента двигателя и передаточных чисел коробки передач и главной передачи. В точке касания колес с поверхностью дороги крутящий момент вызывает окружную силу. Противодействие дороги этой окружной силе выражается реактивной силой, передаваемой от дороги на ведущее колесо. Эта сила направлена в сторону движения автомобиля и называется толкающей или тяговой силой. Тяговая сила от колес передается на ведущий мост и далее на раму, заставляя автомобиль двигаться. Величина тяговой силы тем больше, чем больше крутящий момент двигателя и передаточные числа коробки передач и главной передачи. Тяговая сила на ведущих колесах дости­гает наибольшей величины при движении автомобиля на низшей передаче, поэтому низшую передачу используют при трогании с места автомобиля с грузом, при движении автомобиля по бездорожью. Величина тяговой силы на ведущих колесах автомобиля ограничивается сцеплением шин с поверхностью дороги.

Видео:Центробежная силаСкачать

Сила сцепления колес с дорогой

Трение, возника­ющее между ведущими колесами автомобиля и дорогой, называется силой сцепления. Сила сцепления равна произведению коэф­фициента сцепления на сцепной вес, т. е. вес, приходящийся на ведущие колеса автомобиля. Величина коэффициента сцепления шин с дорогой зависит от качества и состояния дорожного покрытия, формы и состояния рисунка протектора шины, давления воздуха в шине.

У легковых автомобилей полный вес рас­пределяется по осям примерно поровну. Поэтому сцепной вес его можно принять равным 50% полного веса. У грузовых автомоби­лей при полной их на­грузке сцепной вес (вес, приходящийся на заднюю ось) составляет примерно 60—70% полного веса.

Величина коэффициента сцепления имеет большое значение для эксплуатации автомобиля и безопасности движения, так как от него зависят проходимость автомобиля, тормозные качества, возможность, пробуксовки и заноса ведущих колес. При незначи­тельном коэффициенте сцепления трогание автомобиля с места со­провождается пробуксовкой, а торможение — скольжением колес. В результате автомобиль иногда не удается тронуть с места, а при торможении происходит резкое увеличение тормозного пути и возникновение заноса.

На асфальтобетонных покрытиях в жаркую погоду на поверх­ность выступает битум, делая дорогу маслянистой и более скольз­кой, что снижает коэффициент сцепления. Особенно сильно снижается коэффициент сцепления при смачивании дороги первым дождем, когда образуется еще не смытая пленка жидкой грязи. Заснежённая или обледенелая дорога особенно опасна в теплую погоду, когда поверхность подтаивает.

При увеличении скорости движения коэффициент сцепления снижается, в особенности на мокрой дороге, так как выступы ри­сунка протектора шины не успевают продавливать пленку влаги.

Исправное состояние рисунка протектора шины имеет большое значение при движении по грунтовым дорогам, снегу, песку, а также по дорогам с твердым покрытием, по покрытым пленкой грязи или воды. Благодаря наличию выступов рисунка опорная площадь шины уменьшается и, следовательно, возрастает удельное давление на поверхность дороги. При этом легче продавливается грязевая пленка и восстанавливается контакт с дорожным покрытием, а на легком грунте происходит непосредственное зацепление выступов рисунка за грунт.

Повышенное давление воздуха в шине уменьшает ее опорную поверхность, вследствие чего удельное давление возрастает на­столько, что при трогании с места и при торможении может произойти разрушение резины и сцепление колес с дорогой уменьшается.

Таким образом, величина коэффициента сцепления зависит от многих условий и может изменяться в довольно значительных пределах. Так как много дорожно-транспортных происшествий происходит из-за плохого сцепления, то водители должны уметь приблизительно оценивать величину коэффициента сцепления и выбирать скорость движения и приемы управления в соответствии с ним.

Видео:Элементы теории движения автомобиля.Скачать

Сила сопротивления воздуха

При движении автомобиль преодолевает сопротивление воздуха, которое складывается из нескольких сопротивлений:

• лобового сопротивле­ния (около 55—60% всего сопротивления воздуха)
• создаваемого выступающими частями—подножками автобуса или автомобиля, крыльями (12—18%)
• возникающего при прохождении воздуха через радиатор и подкапотное пространство (10—15%) и др.

Передней частью автомобиля воздух сжимается и раздвигает­ся, в то время как в задней части автомобиля создается разреже­ние, которое вызывает образование завихрений.

Сила сопротивления воздуха зависит от величины лобовой, поверхности автомобиля, его формы, а также от скорости движе­ния. Лобовую площадь грузового автомобиля определяют как произведение колеи (расстояние между шинами) на высоту авто­мобиля. Сила сопротивления воздуха возрастает пропорционально квадрату скорости движения автомобиля (если скорость возра­стает в 2 раза, то сопротивление воздуха увеличивается в 4 раза).

Для улучшения обтекаемости и уменьшения сопротивления воздуха ветровое стекло автомобиля располагают наклонно, а вы­ступающие детали (фары, крылья, ручки дверей) устанавливают заподлицо с внешними очертаниями кузова. У грузовых автомоби­лей можно уменьшить силу сопротивления воздуха, закрыв грузо­вую платформу брезентом, натянутым между крышей кабины и задним бортом.

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Сила сопротивления качению

На каждое колесо ав­томобиля постоянно действует вертикальная нагрузка, которая вызывает вертикальную реакцию дороги. При движении автомобиля на него действует сила сопротивления качению, которая возникает вследствие деформации шин и дороги и трения шин о дорогу.

Сила сопротивления качению равна произведению полного веса автомобиля на коэффициент сопротивления качению шин, который зависит от давления воздуха в шинах и качества дорожного покрытия. Вот- некоторые значения коэффициента сопротивления качению шин:

• для асфальтобетонного покрытия— 0,014—0,020
• для гравийного покрытия—0,02—0,025
• для песка—0,1—0,3

Видео:Движение тел по окружностиСкачать

Сила сопротивления подъему

Автомобильная дорога состоит из чередующихся между собой подъемов и спусков и редко имеет горизонтальные участки большой длины.

При движении на подъем автомобиль испытывает дополнитель­ное сопротивление, которое зависит от угла наклона дороги к гори­зонту. Сопротивление подъему тем больше, чем больше вес автомобиля и угол наклона дороги. При подъезде к подъему необходимо правильно оценить возможности преодоления подъема. Если подъем непродолжительный, его преодолевают с разгоном автомобиля перед подъемом. Если подъем продолжительный, его преодолевают на пониженной передаче, переключившись на нее у начала подъема.

При движении автомобиля на спуске сила сопротивления подъему направлена в сторону движения и является движущей силой.

Видео:Центростремительное ускорение. 9 класс.Скачать

Сила сопротивления разгону

Часть тяговой силы при разгоне затрачивается на ускорение вращающихся масс, главным образом маховика коленчатого вала двигателя и колес автомобиля. Для того чтобы автомобиль начал двигаться с определенной скоростью, ему необходимо преодолеть силу сопротивления разгону, равную произведению массы автомобиля на ускорение. При разгоне автомобиля сила сопротивления разгону направлена в сторону, об­ратную движению. При торможении автомобиля и замедлении его движения эта сила направлена в сторону движения автомобиля. Бывают случаи, когда при резком разгоне груз или пассажиры падают из открытого кузова, с сидений мотоцикла, а при резком торможении пассажиры ударяются о лобовое стекло или о перед­ний борт автомобиля. Для того чтобы таких случаев не было, необходимо, плавно увеличивая частоту вращения коленчатого вала двигателя, преодолевать силу сопротивления разгону и плавно осу­ществлять торможение автомобиля.

Видео:Движение по окружностиСкачать

Центр тяжести

На автомобиль, как и на любое другое тело, действует сила тяжести, направленная вертикально вниз. Центром тяжести автомобиля называют такую точку автомобиля, от которой вес автомобиля распределяется равномерно во всех направлениях. У автомобиля центр тяжести располагается между передней и задней осью на высоте около 0,6 м для легковых и 0,7—1,0 м для гру­зовых. Чем ниже расположен центр тяжести, тем устойчивее авто­мобиль против опрокидывания. При загрузке автомобиля грузом центр тяжести поднимается у легковых автомобилей примерно на 0,3—0,4 м, а у грузовых на 0,5 м и более в зависимости от рода груза. При неравномерном укладывании груза центр тяжести может также сместиться вперед, назад или в сторону, при этом будут нарушаться устойчивость автомобиля и легкость управления.

Видео:Урок 90. Движение по окружности (ч.2)Скачать

Устройство автомобилей

Видео:Урок 89. Движение по окружности (ч.1)Скачать

Силовой баланс автомобиля

Силы, действующие на автомобиль при прямолинейном движении

Прямолинейным движением автомобиля будем считать его равномерное или ускоренное движение по горизонтальной или наклонной прямой дороге (без виражей и поворотов). В этом случае на автомобиль действуют следующие силы:

• сила тяжести автомобиля G , приложенная к центру тяжести, находящемся на расстоянии h_ц от поверхности дороги;
• сила сопротивления атмосферного воздуха P_ω , приложенная к центру парусности, расположенному на расстоянии h_ω от поверхности дороги;
• суммарная касательная реакция R_x2 или сила тяги Р_т , направленная по ходу движения автомобиля;
• нормальные реакции дороги на колеса R_z1 и R_z2 , направленные перпендикулярно поверхности дороги;
• сила сопротивления качению колес P_f , направленная в сторону, противоположную движению автомобиля (совпадает с касательной реакцией R_x1 );;
• силы инерции поступательного движения P_j (проявляются при ускоренном движении), приложенная к центру тяжести автомобиля и направленная в сторону, противоположную ускорению;
• сила сопротивления подъему P_α , приложенная к центру тяжести и направленная в сторону, противоположную движению (возникает при движении по дороге с уклоном);
• сила Р_пр на буксирном крюке в случае буксировки прицепа.

На рисунке 1 представлены все эти силы с учетом их направления по отношению к направлению движения автомобиля.

Для дальнейших теоретических выкладок примем следующие условия (допущения):

• Два одноименных колеса (правые и левые) будем рассматривать, как одно.
• Участок дороги на всем протяжении однородный с постоянным углом наклона α к горизонту и не имеет неровностей.
• Нормальные реакции дороги прикладываются к осям колес.
• Деформация шин и грунта (погружение колес в грунт) учитываются при определении силы сопротивления качению, но на схеме не показываются.

Сила тяги Р_т подробно рассмотрена в предыдущей статье. При принятых выше условиях не имеет значения, сколько колес автомобиля являются ведущими и сколько ведомыми.

Сила сопротивления качению

Силой сопротивления качению автомобиля P_j называется сумма сил сопротивления качению всех его колес. В реальных условиях сопротивление качению отдельных колес автомобиля не бывает одинаковым даже при движении автомобиля по дороге с твердым покрытием.
На деформируемых грунтах любое сопротивление качению задних колес, движущихся по уже уплотненному грунту, значительно меньше, чем для передних. Для решения теоретических задач сопротивление качению определяется для автомобиля в целом.
На сопротивление качению влияют:

• нормальная нагрузка на колеса;
• характер и состояние дорожного покрытия;
• удельное давление на грунт;
• скорость движения автомобиля;
• конструкция и состояние пневматических шин.

Нормальная нагрузка обусловлена полным весом автомобиля и влияет на сопротивление качению непосредственно, поскольку реакции дорожного покрытия или грунта можно считать пропорциональными нормальной нагрузке.
Потери, связанные с деформацией резины в шине (гистерезисные потери) зависят от радиальной деформации шины. Эти потери возрастают при увеличении нагрузки.
Кроме того, рост нормальной нагрузки приводит к увеличению удельного давления, а следовательно, и сопротивлению качения.

Дорожное покрытие оказывает существенное влияние на силу сопротивления качению колес P_f в случае, если оно не является твердым. Величина этой силы определяется работой прессования и выдавливанием в стороны грунта при погружении в него колес.

Удельное давление на грунт – это нормальная нагрузка на единицу площади опорного участка шины и может быть определено по формуле:

где c_q – коэффициент, определяемый жесткостью каркаса шины, c_q = 1 + p₀ ;
p₀ – давление воздуха в шинах.

Понижение удельного давления влияет на силу сопротивления качению колес P_f неоднозначно. При понижении давления возрастает деформация шин, вследствие чего растут гистерезисные потери.
В то же время понижение давления значительно уменьшает погружение шин в грунт (при отсутствии твердого покрытия) и тем самым снижает P_f .

Увеличение скорости движения приводит к увеличению потерь в шинах, в частности из-за того, что их упругие свойства не могут быть полностью использованы (часть шины не успевает полностью распрямиться). Кроме того, при повышении скорости деформации возрастает внутреннее трение в покрышке, что также ведет к увеличению P_f .

Большое значение имеют конструкция и состояние шин, их число и диаметр, а также рисунок протектора, форма и расположение грунтозацепов.

Увеличение числа колес приводит к возрастанию суммарных потерь. Чем больше диаметр колеса, чем оно меньше погружается в грунт, а значит, меньше сопротивление качению. Чем крупнее грунтозацепы и рельефнее протектор шины, тем сильнее колесо деформирует грунт, что также приводит к увеличению силы сопротивления качению колес P_f .
На дорогах с твердым покрытием увеличенные грунтозацепы и рельефный рисунок протектора также приводят к увеличению P_f , поскольку в этом случае растут гистерезисные потери в шине.

При изношенном протекторе уменьшается сопротивление качению, но при этом резко ухудшаются сцепные качества шины с дорогой.

Для эксплуатационных расчетов принимаются два допущения:

• сопротивление качению прямо пропорционально нормальной нагрузке на колеса автомобиля;
• для автомобилей с шинами низкого давления (0,15…0,45 МПа) на одном и том же грунте и при одинаковой нагрузке сопротивление качению одинаково независимо от их конструктивных особенностей.

Тогда сила сопротивления качению может быть выражена через нормальную нагрузку (или равную ей реакцию грунта R_z ) и коэффициент пропорциональности, называемый коэффициентом сопротивления качению f :

Коэффициент сопротивления качению f зависит от характера и состояния дорожного покрытия. Так, для асфальта, бетона или асфальтобетона он равен 0,1…0,3, для укатанной сухой грунтовой дороги – 0,02…0,03, для разбитой мокрой грунтовой дороги – 0,1…0,25, для обледенелой дороги – 0,01…0,03 и т. д.

Влияние скорости движения на коэффициент f сопротивления качению учитывает эмпирическая формула:

где f₀ – коэффициент сопротивления качению при движении автомобиля со скоростью менее 15 м/с;
v – скорость автомобиля.

Сила тяжести и сопротивление движению

Сила тяжести G обусловлена массой m автомобиля, указываемой в его технической характеристике и может быть определена по известной формуле: G = mg , где g – ускорение свободного падения.

Масса снаряженного автомобиля – масса автомобиля без груза, полностью заправленного топливом, смазочными материалами и охлаждающей жидкостью, с запасным колесом, инструментом и оборудованием.
Полная масса автомобиля включает в себя еще массу водителя и груза по номинальной грузоподъемности (для грузового автомобиля) или по номинальной пассажировместимости (для автобусов и легковых автомобилей).
В расчетах обычно принимается полная масса.

Положение центра масс определяется у двухосного автомобиля расстояниями l₁ и l₂ до геометрических осей вращения колес соответственно переднего и заднего мостов. У трехосного автомобиля l₂ – расстояние от центра масс до оси балансира задней тележки.
Расстояние L = l₁ + l₂ называют базой автомобиля.

При движении автомобиля по наклонному участку дороги с углом подъема α сила тяжести раскладывается на две составляющие:

• G cosα – нормальная нагрузка автомобиля на дорогу, перпендикулярная дороге;
• G sinα – сила сопротивления подъему (при спуске — скатывающая сила), обозначается P_α и направлена параллельно поверхности дороги: P_α = G sinα .

На крутых подъемах сопротивление подъему значительно превышает сопротивление качению. Так, при α = 20˚ P_α будет равна примерно 0,36 G , при α = 30˚ Р_α = 0,5 G , тогда как P_f редко превышает 0,05…0,08 G .

При небольших значениях угла α синус может быть заменен тангенсом. В дорожном строительстве тангенс угла наклона дороги к горизонту называют продольным уклоном i , выражаемым в процентах. В этом случае сила сопротивления подъему равна:

Сила сопротивления качению и сила сопротивления подъему зависят от дорожных условий, так как коэффициент сопротивления качению f и угол подъема дороги α в совокупности определяют качество дороги, поэтому можно ввести такое понятие, как сила сопротивления дороги:

При движении автомобиля по наклонной дороге сила сопротивления качению определится из соотношения:

Получим следующую формулу для вычисления силы сопротивления дороги:

P_ψ = G(f cosα + sinα) ≈ G(f + i) .

Выражение в скобках называется коэффициентом сопротивления дороги и обозначается ψ :

ψ = f cosα + sinα .

Тогда сила сопротивления дороги:

Сила инерции

Сила инерции (или сила сопротивления разгону) при поступательном движении автомобиля может быть определена из соотношения:

где j – ускорение автомобиля, m – масса автомобиля.

Так как в автомобиле имеются вращающиеся детали значительной массы, то они также влияют на сопротивление разгону автомобиля, создавая инерционные моменты.
Максимальный инерционный момент сопротивления изменению угловой скорости создают маховик двигателя и колеса, а также массивные детали агрегатов и узлов трансмиссии.
Чтобы учесть влияние вращающихся масс вводят коэффициент учета вращающихся масс δ_вр , который показывает, во сколько раз сила, необходимая для разгона с заданным ускорением поступательно движущихся и вращающихся масс автомобиля, больше силы, необходимой для разгона только его поступательно движущихся масс.

С учетом коэффициента δ_вр уравнение (1) будет иметь вид:

Значение коэффициента δ_вр определяется по формуле:

где j_м – момент инерции маховика; η_тр – КПД трансмиссии; i_тр – передаточное число трансмиссии; j_к – суммарный момент инерции всех колес автомобиля; m – масса автомобиля; r – радиус колеса.

Энергия, затрачиваемая на разгон деталей двигателя на прямой передаче, в два-три раза, а на низших передачах в восемь-десять раз больше энергии, расходуемой на разгон колес.

В случае, если точное значение моментов инерции маховика и колес неизвестно, то коэффициент учета вращающихся масс δ_вр определяют по эмпирической формуле:

где δ₁ ≈ δ₂ от 0,03 до 0,05; m_а – масса автомобиля с полной нагрузкой; m – фактическая масса автомобиля.

При движении автомобиля с отключенной от двигателя трансмиссией коэффициент учета вращающихся масс может быть приближенно определен по формуле:

Сила сопротивления воздуха

Как и всякое тело, перемещающееся в воздушной среде, автомобиль со стороны атмосферного воздуха испытывает сопротивление движению, которое обуславливается двумя факторами: трением, возникающим в пограничных с поверхностью автомобиля слоях воздуха, и вихреобразованием в окружающих его потоках.

Движущийся автомобиль увлекает за собой непосредственно прилегающий к нему слой воздуха, который взаимодействует на соседний с ним слой и т. д., увлекая его за собой. Скорость каждого последующего слоя воздуха меньше, чем предыдущего, что и вызывает силы трения между слоями. Чем выше скорость движения автомобиля, тем большие массы воздуха будут увлекаться в движение, и тем больше суммарная сила трения, возникающая между слоями и поверхностью автомобиля.
Однако при скоростях, с которыми передвигаются автомобили, сопротивление, вызываемое трением в пограничных с автомобилем слоях очень мало, и им можно пренебречь в большинстве расчетов.

Образование вихревых потоков можно представить, предположив, что на неподвижный автомобиль направлен с достаточной скоростью поток воздуха. Ударяясь о лобовую поверхность кабины и кузова автомобиля, струи воздуха изменяют направление своего движения (рис. 1). При этом чем менее обтекаемую форму имеет автомобиль, тем интенсивнее и объемнее будут вызываемые им завихрения воздушных струй.
В результате вихреобразования возникает разрежение воздуха сзади автомобиля, тогда как перед ним воздух уплотняется, вследствие чего создается разность давлений воздуха впереди и сзади автомобиля.

Сопротивление воздуха при вихреобразовании зависит от площади поперечного сечения автомобиля (лобовой проекции), и особенно от его формы.
Усилению вихреобразования способствует наличие выступающих частей, прямых углов и резких переходов в профильной проекции автомобиля. Обтекаемые формы современных легковых, и особенно – гоночных автомобилей, существенно снижают сопротивление воздуха, вызываемое вихреобразованием.

Сопротивление воздуха при проектировании кузовов автомобилей определяют чаще всего опытным путем с помощью аэродинамической трубы, которая позволяет получить равномерный прямолинейный установившийся воздушный поток заданной скорости и даже температуры. В аэродинамической трубе можно не только исследовать обтекаемость автомобиля, но и определить эффективность очистки ветрового стекла и ряд других параметров, связанных с воздействием воздушного потока на автомобиль.

Для расчета силы сопротивления воздуха P_ω аналитическими методами можно использовать формулу, полученную опытным путем (эмпирическая зависимость), которая справедлива для всех скоростей автомобиля, кроме самых малых:

где ρ – плотность воздуха;
c – коэффициент сопротивления воздуха, зависящий от формы автомобиля;
F – площадь лобового сопротивления, т. е. площадь проекции автомобиля на плоскость, перпендикулярную направлению движения;
v – скорость автомобиля.

Считая, что плотность ρ воздуха в реальных условиях движения автомобиля величина относительно постоянная, вводят понятие коэффициента k_ω обтекаемости автомобиля, который тоже можно считать постоянной величиной:

Тогда формула (3) примет вид:

Значения коэффициента обтекаемости зависят от формы кузова. Так, например, для автобусов капотной компоновки он равен 0,45…0,55, для автобусов вагонной компоновки – 0,35…0,45, для легковых автомобилей – 0,2…0,35, для гоночных автомобилей – 0,15…0,2 и т. д.

Площадь лобового сопротивления с достаточной степенью точности (погрешность не более 10%) можно определить по следующим зависимостям:

• для грузового автомобиля F = BH , где H – высота автомобиля; B – колея автомобиля;
• для легковых автомобилей F = 0,78 B_aH , где B_a – наибольшая ширина автомобиля.

При расчетах силы сопротивления воздуха P_ω важно определить место приложения данной силы, так называемый центр парусности.

Точное положение центра парусности автомобиля определяется опытным путем в аэродинамической трубе. Для приблизительных расчетов принимают высоту положения центра парусности равной половине высоты автомобиля, а его расположение по горизонтали – на оси симметрии лобовой проекции автомобиля.

При скоростях выше 100…120 км/ч со стороны воздушных потоков на автомобиль начинает действовать так называемая подъемная сила, имеющая аэродинамическую природу, направленная вертикально вверх и стремящаяся оторвать автомобиль от поверхности дороги.
Это негативное явление приводит к потере устойчивости и управляемости автомобиля, и связано с тем, что под днищем автомобиля, благодаря его плоской форме, скорость потока воздуха ниже, а давление в воздушном потоке выше, чем над автомобилем, где, благодаря ускорению воздушных масс из-за криволинейной формы кузова автомобиля, давление снижается. В результате на автомобиль начинает действовать подъемная сила, аналогичная подъемной силе, действующей на крыло самолета.
У спортивных автомобилей благодаря специальной форме кузова и использованию аэроэлементов (антикрыло) эту силу направляют вниз, увеличивая сцепление колес с дорогой.

Силы, возникающие при буксировке прицепов

В случае буксировки прицепа с помощью буксирного устройства на крюке возникает сила Р_пр , которая тоже направлена в сторону, противоположную силе тяги.
Разложив силу Р_пр на составляющие можно записать:

где G’ , P’_j , P’_f – соответственно сила тяжести, силы сопротивления инерции и качению колес прицепа.

Сила сопротивления воздуха для прицепа в приближенных расчетах не учитывается, так как она прилагается к центру парусности тягача. Кроме того, автопоезда не передвигаются на больших скоростях, когда сила сопротивления воздуха достигает существенных значений.

Нормальная реакция дороги

Нормальная реакция дороги R_z не совершает ни полезной работы, ни работы сопротивления движению, поскольку направлена перпендикулярно направлению движения автомобиля. Однако при изучении тягово-скоростных свойств автомобиля их необходимо учитывать, поскольку R_z определяет силы сопротивления качению и сцепление колес с опорной поверхностью (дорогой).
Нормальные реакции необходимы при оценке таких эксплуатационных свойств автомобиля, как торможение, управляемость, устойчивость и проходимость, а также при расчетах мостов.

Сила тяжести G автомобиля распределяется по всем его колесам, и со стороны дороги действуют соответствующие нормальные реакции на каждое колесо. При этом равномерное распределение массы автомобиля на его колеса хотя и могут иметь место, но в порядке исключения. Поэтому на разные колеса автомобиля действуют разные по величине нормальные реакции, в соответствии с распределением нагрузки на оси и мости, а также на каждое колесо.

Рассмотрим силы, действующие на автомобиль, стоящий на горизонтальной поверхности (рис. 2, а).
Из центра тяжести автомобиля действует вектор силы тяжести G , расположенный на расстоянии l₁ от передней оси, и на расстоянии l₂ от оси заднего моста. В соответствии с законами статики нормальные реакции R_z1 и R_z2 на колеса передней и задней оси обратно пропорциональны расстоянию от центра тяжести до этих осей:

где L – расстояние между осями автомобиля.

Во время движения нормальные реакции дороги изменяются под действием различных сил и моментов. На рис. 2,б показана схема сил, действующих на автомобиль при его разгоне и на подъеме. Расчетным путем можно доказать, что нормальнее реакции дороги на передние колеса уменьшаются, а на задние увеличиваются с ростом крутизны подъема, интенсивности разгона, а также с увеличением силы сопротивления воздуха движению автомобиля.

Изменение динамических нормальных реакций относительно статических учитывает коэффициент изменения нормальных реакций m_p , который представляет собой отношение нормальных реакций, действующих на мост автомобиля при его движении, к реакциям, действующим на этот же мост неподвижного автомобиля:

Во время разгона автомобиля предельные значения коэффициентов составляют:
m_p1 от 0,55 до 0,7; m_p2 от 1,2 до 1,35, т. е. во время разгона нагрузка на передний мост уменьшается, а на задний увеличивается по сравнению с нагрузками в статическом положении.
При торможении автомобиля наблюдается обратное явление. Это объясняется тем, что при разгоне автомобиль как бы «приседает» на задние колеса, а при торможении испытывает «кивок» вперед.

🔍 Видео

Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

24 Элементы теории автомобиля Силы действующие на автомобильСкачать

Видеолекция Силы, действующие на автомобиль при движенииСкачать

Формулы механики 2, движение по окружности, центростремительное ускорениеСкачать

Как работает колесоСкачать

Движение колеса без проскальзывания, качение | Олимпиадная физика, кинематика | 9 – 11 классСкачать

ДВИЖЕНИЕ ПО ОКРУЖНОСТИ 9 класс физика ПерышкинСкачать

Элементы теории автомобиля|Теория движения автомобиля: основные элементыСкачать

Физика | Равномерное движение по окружностиСкачать