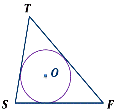Какие из данных многоугольников описаны около окружности

Презентация была опубликована 6 лет назад пользователемМаксим Шишов

Похожие презентации

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Презентация на тему: » Многоугольники, описанные около окружности Многоугольник называется описанным около окружности, если все его стороны касаются этой окружности. Сама окружность.» — Транскрипт:

1 Многоугольники, описанные около окружности Многоугольник называется описанным около окружности, если все его стороны касаются этой окружности. Сама окружность при этом называется вписанной в многоугольник.

2 Теорема 1 В любой треугольник можно вписать окружность. Ее центром будет точка пересечения биссектрис этого треугольника.

3 Теорема 2 В любой правильный многоугольник можно вписать окружность. Ее центром является точка пересечения биссектрис углов многоугольника.

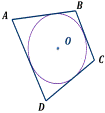
4 Теорема 3 В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны, т.е. AB + CD = AD + BC.

5 Вопрос 1 Какой многоугольник называется описанным около окружности? Ответ: Многоугольник называется описанным около окружности, если все его стороны касаются этой окружности.

6 Вопрос 2 Какая окружность называется вписанной в многоугольник? Ответ: Вписанной в многоугольник называется окружность, касающаяся всех сторон этого многоугольника.

7 Вопрос 3 Во всякий ли треугольник можно вписать окружность? Ответ: Да.

8 Вопрос 4 Какая точка является центром вписанной в треугольник окружности? Ответ: Центром вписанной окружности является точка пересечения биссектрис этого треугольника.

9 Вопрос 5 В любой ли правильный многоугольник можно ли вписать окружность? Ответ: Да.

10 Вопрос 6 Можно ли вписать окружность в: а) остроугольный треугольник; б) прямоугольный треугольник; в) тупоугольный треугольник? Ответ: а) Да; б) да; в) да.

11 Вопрос 7 Может ли центр вписанной в треугольник окружности находиться вне этого треугольника? Ответ: Нет.

12 Вопрос 8 Какой вид имеет треугольник, если: а) центры вписанной и описанной около треугольника окружностей совпадают; б) центр вписанной в него окружности принадлежит одной из его высот? Ответ: а) Равносторонний; б) равнобедренный.

13 Упражнение 1 Укажите центр окружности, вписанной в квадрат ABCD. Ответ:

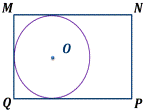
14 Упражнение 2 Укажите центр окружности, вписанной в квадрат ABCD. Ответ:

15 Упражнение 3 Укажите центр окружности, вписанной в ромб ABCD. Ответ:

16 Упражнение 4 Укажите центр окружности, вписанной в треугольник ABC. Ответ:

17 Упражнение 5 Укажите центр окружности, вписанной в треугольник ABC. Ответ:

18 Упражнение 6 Ответ: 2. Найдите радиус окружности, вписанной в квадрат со стороной 4.

19 Упражнение 7 Ответ: 6. Найдите сторону квадрата, описанного около окружности радиуса 3.

20 Упражнение 8 Ответ: 10. Найдите высоту трапеции, в которую вписана окружность радиуса 5.

21 Упражнение 9 Окружность, вписанная в треугольник ABC, делит сторону AB в точке касания D на два отрезка AD = 5 см и DB = 6 см. Найдите периметр треугольника ABC, если известно, что BC = 10 см. Ответ: 30 см.

22 Упражнение 10 Ответ: 20 см. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, которые равны 4 см и 3 см, считая от вершины. Найдите периметр треугольника.

23 Упражнение 11 К окружности, вписанной в треугольник АВС, проведены три касательные. Периметры отсеченных треугольников равны p 1, p 2, p 3. Найдите периметр данного треугольника. Ответ: p 1 + p 2 + p 3.

24 Упражнение 12 Ответ: 34 см. В равнобедренном треугольнике боковые стороны делятся точками касания вписанной в треугольник окружности в отношении 7:5, считая от вершины, противоположной основанию. Найдите периметр треугольника, если его основание равно 10 см.

25 Упражнение 13 Ответ: а) Нет; Всегда ли можно ли вписать окружность в: а) прямоугольник; б) параллелограмм; в) ромб; г) квадрат; д) дельтоид ? б) нет; в) да; г) да; д) да.

26 Упражнение 14 Два равнобедренных треугольника имеют общее основание и расположены по разные стороны от него. Можно ли в образованный ими выпуклый четырехугольник вписать окружность? Ответ: Да.

27 Упражнение 15 Можно ли вписать окружность в четырехугольник, стороны которого последовательно равны 1, 2, 3, 4? Ответ: Нет.

28 Упражнение 16 Какой вид имеет четырехугольник, если центр вписанной в него окружности совпадает с точкой пересечения диагоналей? Ответ: Ромб.

29 Упражнение 17 Около окружности описана трапеция, периметр которой равен 18 см. Найдите ее среднюю линию. Ответ: 4,5 см.

30 Упражнение 18 В трапецию, периметр которой равен 56 см, вписана окружность. Три последовательные стороны трапеции относятся как 2:7:12. Найдите стороны трапеции. Ответ: 4 см, 14 см, 24 см, 14 см.

31 Упражнение 19 Боковые стороны трапеции, описанной около окружности, равны 2 см и 4 см. Найдите среднюю линию трапеции. Ответ: 3 см.

32 Упражнение 20 Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности. Ответ: 2.

33 Упражнение 21 Докажите, что если в трапецию ABCD (AB||CD) вписана окружность с центром O, то углы AOD и BOC равны 90 о. Доказательство. Лучи AO и DO являются биссектрисами внутренних односторонних углов при параллельных прямых AB и CD. Следовательно, угол AOD равен 90 о. Аналогично, угол BOC равен 90 о.

34 Упражнение 22 Докажите, что если в равнобедренную трапецию ABCD (AB||CD) вписана окружность, ее боковые стороны AD и BC равны средней линии EF. Доказательство. Сумма боковых сторон трапеции равна сумме оснований. Следовательно, боковая сторона равна полусумме оснований, т.е. равна средней линии.

35 Упражнение 23 Три последовательные стороны четырехугольника, в который можно вписать окружность, равны 6 см, 8 см и 9 см. Найдите четвертую сторону и периметр этого четырехугольника. Ответ: 7 см, 30 см.

36 Упражнение 24 Противоположные стороны четырехугольника, описанного около окружности, равны 7 см и 10 см. Можно ли по этим данным найти периметр четырехугольника? Ответ: Да, 34 см.

37 Упражнение 25 Периметр четырехугольника, описанного около окружности, равен 24, две его стороны равны 5 и 6. Найдите большую из оставшихся сторон. Ответ: 7.

38 Упражнение 26 К окружности, вписанной в треугольник АВС, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника. Ответ: 24.

39 Упражнение 27 В шестиугольнике ABCDEF, описанном около окружности AB = 3, CD = 4, EF = 2. Найдите периметр этого шестиугольника. Ответ: 18.

40 Упражнение 28* Можно ли вписать окружность в пятиугольник, стороны которого последовательно равны 1, 2, 1, 2, 1? Ответ: Нет. Если в пятиугольник можно вписать окружность, то сумма любых двух его не соседних сторон меньше суммы трех оставшихся сторон.

41 Упражнение 29* Можно ли вписать окружность в шестиугольник, стороны которого последовательно равны 1, 2, 1, 2, 1, 2? Ответ: Нет. Если в шестиугольник можно вписать окружность, то сумма любых трех его не соседних сторон равна сумме трех оставшихся сторон.

42 Упражнение 30* Стороны пятиугольника, описанного около окружности, последовательно равны 1, 2, 3, 2, 1. Найдите радиус этой окружности, если угол, заключенный между сторонами, равными 1, равен 120 о. Ответ:

Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Тест: Вписанная и описанная окружности

Вписанная и описанная окружности

В равнобедренном треугольнике точка касания вписанной окружности делит боковую сторону на отрезки длиной 12 см и 3 см, считая от отнования. Найдите площадь треугольника. (в ответе укажите только число без единицы измерения)

Дополните определение:
Если все стороны многоугольника касаются окружности, то окружность называется .

Если около четырехугольника можно описать окружность, то .

Выберите один из 4 вариантов ответа:

1) сумма противоположных углов равна 180 0 .

2) суммы противоположных сторон равны.

3) суммы смежных сторон равны.

4) сумма соседних углов равна 180 0 .

Какие из данных многоугольников описаны около окружности?

Выберите несколько из 3 вариантов ответа:

1)

2)

3)

Найдите стороны остроугольного равнобедренного треугольника, если высота, проведенная к его основанию, равна 8 см, а радиус окружности, в которую он вписан 5 см.

Выберите несколько из 5 вариантов ответа:

1)

2)

Дополните определение:
Если все вершины многоугольника лежат на окружности, то окружность называется .

Окружность можно вписать в любой треугольник?

Выберите один из 5 вариантов ответа:

1) только в равносторонний.

2) в треугольник нельзя вписать окружность.

4) только в равнобедренный.

5) только в прямоугольный.

Если в четырехугольник можно вписать окружность, то .

Выберите один из 4 вариантов ответа:

1) суммы его смежных сторон равны.

2) сумма соседних углов равна 180 0 .

3) сумма противоположных углов равна 180 0 .

4) суммы его противоположных сторон равны.

Выберите верные утверждения:

Выберите несколько из 5 вариантов ответа:

1) Треугольник нельзя описать около окружности.

2) Около квадрата нельзя описать окружность.

3) Прямоугольник нельзя описать около окружности.

4) Около прямоугольника можно описать окружность.

5) Ромб можно описать около окружности.

Какие из данных многоугольников вписаны в окружность?

Выберите несколько из 3 вариантов ответа:

1)

2)

3)

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Вписанные и описанные многоугольники

Вписанным в круг многоугольником называется такой многоугольник, вершины которого лежат на окружности. Описанным около круга многоугольником называется такой многоугольник, стороны которого касаются окружности.

Описанной около многоугольника окружностью называется окружность, проходящая через его вершины. Вписанной в многоугольник окружностью называется окружность, касающаяся его сторон.

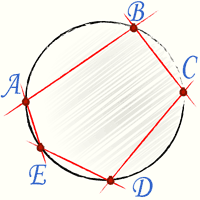Вписанный многоугольник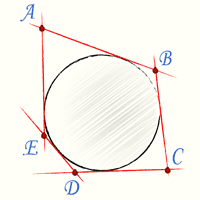

Описанный многоугольник

Если многоугольник взят произвольно, то в него нельзя вписать и около него нельзя описать окружность. Только многоугольники соответствующие некоторым правилам можно описать окружностью или вписать в них окружность.

Видео:110. Окружность, описанная около правильного многоугольникаСкачать

Правила для многоугольников которые можно вписать в окружность и описать окружность вокруг них

Для треугольника всегда возможны и вписанная окружность и описанная окружность.

Для четырехугольника окружность можно вписать только в том случае, если суммы его противоположных сторон одинаковы. Из всех параллелограммов только в ромб и квадрат можно вписать окружность. Ее центр лежит на пересечении диагоналей.

Вокруг четырехугольника окружность можно описать только если сумма противоположных углов равна 180°. Из всех параллелограммов только около прямоугольника и квадрата можно описать окружность. Ее центр лежит на пересечении диагоналей.

Вокруг трапеции возможно описать окружность или в трапецию можно вписать окружность если трапеция равнобокая.

🌟 Видео

Всё про углы в окружности. Геометрия | МатематикаСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4Скачать

Геометрия Доказательство Площадь многоугольника, описанного около окружности равна произведению егоСкачать

8 класс, 39 урок, Описанная окружностьСкачать

Построить описанную окружность (Задача 1)Скачать

Геометрия 8 класс (Урок№33 - Описанная окружность.)Скачать

Описанная окружностьСкачать

Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать