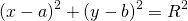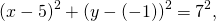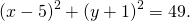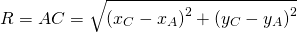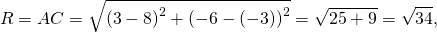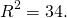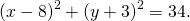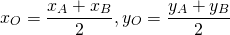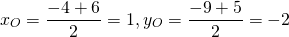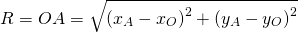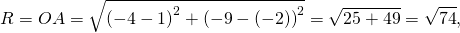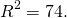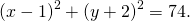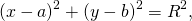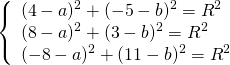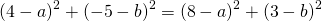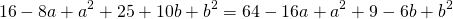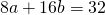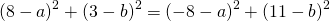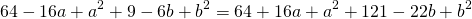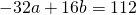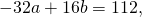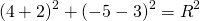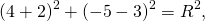Как записывать уравнения окружности зная координаты

Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.

1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.

Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:

Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:

2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).

Так как центр окружности — точка A(8; -3), то a=8, b=-3.

Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.

Следовательно, уравнение данной окружности

3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).

Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка

Центр окружности — точка O(1;-2). Значит, a=1, b=-2.

Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,

Таким образом, уравнение окружности с диаметром AB —

4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).

Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение

получаем систему уравнений:

Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим

Приравняем правые части 2-го и 3-го уравнений:

на -1 и сложив результат почленно с уравнением

получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:

Следовательно, уравнение окружности, проходящей через три данные точки —

5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).

Решение аналогично решению задания 4. В результате получим уравнение

Видео:Уравнение окружности (1)Скачать

Как записать уравнение окружности по координатам

Видео:Составляем уравнение прямой по точкамСкачать

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

что и требовалось доказать.

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

Видео:№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

Написать уравнение окружности

Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.

1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.

Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:

Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:

2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).

Так как центр окружности — точка A(8; -3), то a=8, b=-3.

Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.

Следовательно, уравнение данной окружности

3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).

Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка

Центр окружности — точка O(1;-2). Значит, a=1, b=-2.

Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,

Таким образом, уравнение окружности с диаметром AB —

4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).

Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение

получаем систему уравнений:

Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим

Приравняем правые части 2-го и 3-го уравнений:

на -1 и сложив результат почленно с уравнением

получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:

Следовательно, уравнение окружности, проходящей через три данные точки —

5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).

Решение аналогично решению задания 4. В результате получим уравнение

Видео:УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Уравнение окружности.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

,

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Уравнение окружности.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

,

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

🌟 Видео

№965. Напишите уравнения окружностей с центром в начале координат и радиусами r1=3, r2= √2 , r3=5/2.Скачать

9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

Уравнение окружности ? Окружность в системе координат / Функция окружностиСкачать

Составляем уравнение окружностиСкачать

Уравнение окружностиСкачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

ПРОСТОЙ СЕКРЕТ ДЛЯ НАЧИНАЮЩИХ! Реши алгебру за 12 минут — Уравнение ОкружностиСкачать

№969. Напишите уравнение окружности с диаметром MN, если: а) М (-3; 5),Скачать

Составить уравнение окружности. Геометрия. Задачи по рисункам.Скачать

Геометрия 9 класс (Урок№9 - Уравнение линии на плоскости. Уравнение окружности. Уравнение прямой.)Скачать