Как разделить окружность на заданное количество одинаковых частей, терминология при построении окружности, деление окружности на 3, 4, 5, 6, 8, 10 частей.
- Термины при построениях окружности
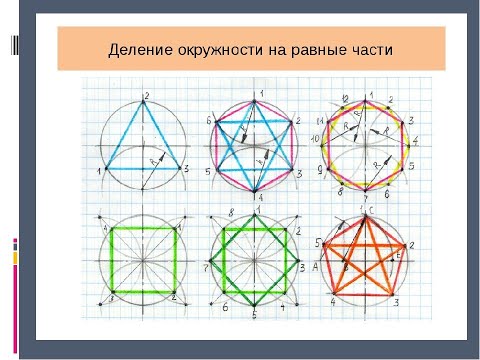
- Деление окружности на 4 и 8 одинаковых частей
- Деление окружности на 3 и 6 равных частей (кратные 3 трём)
- Деление окружности на 5 и 10 равных частей
- Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)
- Нахождение центра дуги окружности
- Делим окружность на 16 частей
- Делим окружность на 16 частей
- 💡 Видео
Термины при построениях окружности
Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром.
Прямые линии, соединяющие любую точку окружности с её центром, называют радиусами R.
Прямая АВ, соединяющая две точки окружности и проходящая через её центр О, называется диаметром D.
Части окружностей называются дугами.
Прямая СD, соединяющая две точки на окружности, называется хордой.
Прямая МN,которая имеет только одну общую точку с окружностью называется касательной.
Часть круга, ограниченная хордой СD и дугой, называется сигментом.
Часть круга, ограниченная двумя радиусами и дугой, называется сектором.
Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности.
Угол, образованный двумя радиусами КОА, называется центральным углом.
Два взаимно перпендикулярных радиуса составляют угол в 90 0 и ограничивают 1/4 окружности.
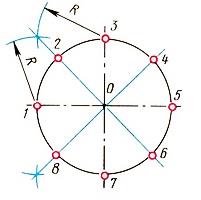
Видео:Построение шестнадцатиугольника циркулемСкачать

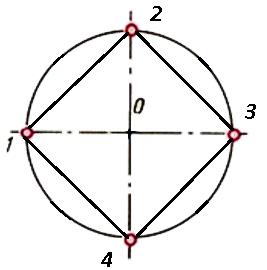
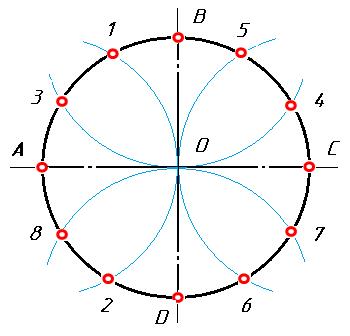
Деление окружности на 4 и 8 одинаковых частей
Проводим окружность с горизонтальной и вертикальной осями, которые делят её на 4-ре равные части. Проведённые с помощью циркуля или угольника под 45 0 , две взаимно перпендикулярные линии делят окружность на 8-мь равных частей.
Видео:Деление окружностиСкачать

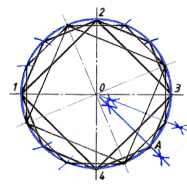
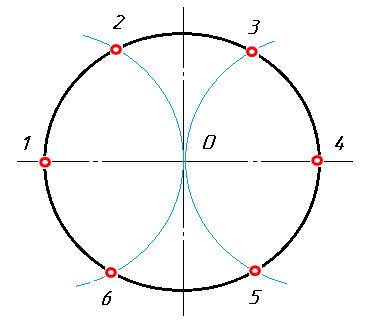
Деление окружности на 3 и 6 равных частей (кратные 3 трём)
Для деления окружности на 3, 6 и кратное им количество частей, проводим окружность заданного радиуса и соответствующие оси. Деление можно начинать от точки пересечения горизонтальной или вертикальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6-ть раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шести-угольник. Соединение точек через одну даёт равносторонний треугольник, и деление окружности на три равные части.
Видео:Деление окружности на n- равные частиСкачать

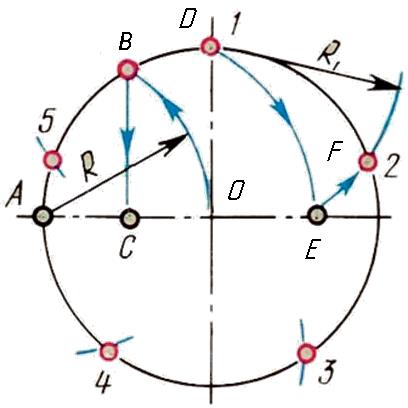
Деление окружности на 5 и 10 равных частей
Построение правильного пятиугольника выполняется следующим образом. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки «а» в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке «b». Радиусом R3 из точки «1» проводят дугу окружности до пересечения с заданной окружностью (т.5) и получают сторону правильного пятиугольника. Расстояние «b-О» даёт сторону правильного десятиугольника.
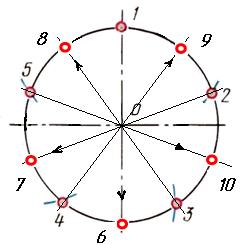
Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)
Выполняется следующим образом. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки «1» окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей на которое мы делим данную окружность, например 9. Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Проводим линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через чётные ( или нечётные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т.к. точки 1, 2, …. 9 делят окружность на 9-ть ( N ) равных частей.
Видео:Красивое деление окружности на 20 частей циркулемСкачать

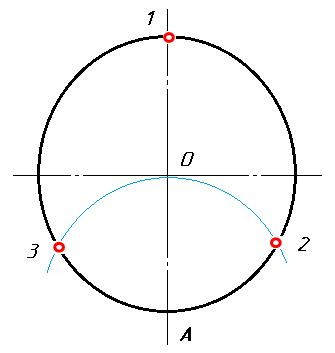
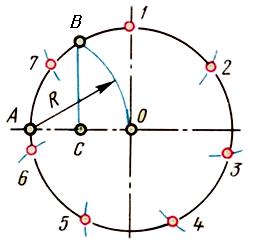
Нахождение центра дуги окружности
Для нахождения центра дуги окружности нужно выполнить следующие построения: на данной дуге отмечаем четыре произвольные точки А, В, С, D и соединяем их попарно хордами АВ и СD. Каждую из хорд при помощи циркуля делим пополам, получив, таким образом, перпендикуляр, проходящий через середину соответствующей хорды. Взаимное пересечение этих перпендикуляров даёт центр данной дуги и соответствующей ей окружности.
Видео:Построение шестнадцатиугольника циркулемСкачать

Делим окружность на 16 частей
Раздел 3: Чтение и выполнение чертежей (7 часов)
Выполнение чертежей предметов с использованием геометрических построений (деление окружности на равные части, деление углов и отрезков на равные части; сопряжения). Общее понятие о форме и формообразовании предметов. Анализ геометрической формы предметов. Способы чтения и выполнения чертежей на основе анализа формы. Построение третьей проекции предмета по двум заданным. Нахождение на чертеже вершин, ребер и граней, поверхностей геометрических тел, составляющих форму предмета. Определение необходимого и достаточного количества видов на чертеже. Творческие задачи на пройденный материал.
Урок № 11: Деление окружности на равные части
 Предыдущий урок Предыдущий урок |  Поурочное планирование Поурочное планирование  | Следующий урок  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Число делений | Коэффици- ент | Число делений | Коэффици- ент | Число делений | Коэффици- ент |
| 3 | 0,866 | 13 | 0,239 | 23 | 0,136 |
| 4 | 0,707 | 14 | 0,222 | 24 | 0,130 |
| 5 | 0,588 | 15 | 0,208 | 25 | 0,125 |
| 6 | 0,5 | 16 | 0,195 | 26 | 0,120 |
| 7 | 0,434 | 17 | 0,184 | 27 | 0,116 |
| 8 | 0,383 | 18 | 0,174 | 28 | 0,112 |
| 9 | 0,342 | 19 | 0,164 | 29 | 0,108 |
| 10 | 0,309 | 20 | 0,156 | 30 | 0,104 |
| 11 | 0,282 | 21 | 0,149 | 31 | 0,101 |
| 12 | 0,259 | 22 | 0,142 | 32 | 0,098 |
Пользоваться таблицей очень просто. В столбце 1, 3 и 5 стоят числа, на которые нужно разбить окружность, а в столбцах 2, 4 и 6 — коэффициент, относящийся к диаметру данной окружности. Пример: у нас имеется болванка диам. = 50 мм, ее нужно разбить на 25 частей (для шпилек). Число 25 находится в 5 столбце, а в шестом его коэффициент = 0,125. Берем данный д. = 50 мм и умножим на коэффициент, равный 0,125, получим 50 x 0,125 = 6,25 мм. На полученное расстояние — 6,25 мм и нужно развести ножки циркуля и им шагать по линии окружности.
Еще пример: имеется окружность диам. = 60 мм. Ее нужно разбить на 13 частей. По предыдущему примеру решаем 60 х 0,239 = 14,34.
При пользовании данной таблицей необходимо следить за тем, чтобы ножка циркуля точно ставилась на линию окружности, иначе она может в конечном счете не притти к делению, откуда начата отсечка.
На линейке очень трудно наглаз найти сотые мм, напр. 6,34. Здесь можно поступить так: брать не 34 сотых, а 25, т. е. четверть мм.
💡 Видео
Деление окружности на 3; 6; 12 равных частейСкачать

деление окружности на произвольное число частейСкачать
Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Построение 8 угольника циркулемСкачать

Построение 10 угольника циркулемСкачать

Как разделить круг на равные частиСкачать

Деление окружности на равные части с помощью циркуляСкачать

Деление окружности на 3 частиСкачать

Деление окружности на 12 равных частейСкачать

Как разделить окружность на 10 частей How to divide a circle into 10 partsСкачать

1 2 2 деление окружности на 5 равных частейСкачать

КАК РАЗДЕЛИТЬ ОКРУЖНОСТЬ НА 12 РАВНЫХ ЧАСТЕЙ?Скачать

🧭Как разделить круг на ТРИ Части, без Линейки и Циркуля; How to split a circle into three partsСкачать

Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать










 pdf Проведение параллельных прямых
pdf Проведение параллельных прямых