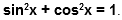Как вычислить значение выражения используя единичную окружность

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Тригонометрическая окружность. Как выучить?Скачать

Единичная окружность в тригонометрии

Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.

Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.

Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.

Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.

Поясним, как единичная окружность связана с тригонометрией.

В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.

Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.

Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.

Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:

• Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
• Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
• В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
• В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.

Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:

Радиан — одна из мер для определения величины угла.

Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.

Число радиан для полной окружности — 360 градусов.

Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.

Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.

Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:

• 2π радиан = 360°
• 1 радиан = (360/2π) градусов
• 1 радиан = (180/π) градусов
• 360° = 2π радиан
• 1° = (2π/360) радиан
• 1° = (π/180) радиан

Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.

Уравнение единичной окружности

При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Видео:Как искать точки на тригонометрической окружности.Скачать

Геометрия. Урок 1. Тригонометрия

Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Тригонометрия в прямоугольном треугольнике

Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.

sin α = Противолежащий катет гипотенуза

Косинус угла – отношение прилежащего катета к гипотенузе.

cos α = Прилежащий катет гипотенуза

Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).

tg α = Противолежащий катет Прилежащий катет

Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).

ctg α = Прилежащий катет Противолежащий катет

Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:

sin ∠ A = C B A B

cos ∠ A = A C A B

tg ∠ A = sin ∠ A cos ∠ A = C B A C

ctg ∠ A = cos ∠ A sin ∠ A = A C C B

sin ∠ B = A C A B

cos ∠ B = B C A B

tg ∠ B = sin ∠ B cos ∠ B = A C C B

ctg ∠ B = cos ∠ B sin ∠ B = C B A C

Видео:Как запомнить тригонометрический круг специально ничего не выучивая?Скачать

Тригонометрия: Тригонометрический круг

Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.

Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.

Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )

На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.

Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .

Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .

Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .

Рассмотрим прямоугольный треугольник A O B :

cos α = O B O A = O B 1 = O B

sin α = A B O A = A B 1 = A B

Поскольку O C A B – прямоугольник, A B = C O .

Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).

Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :

Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .

Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .

Координата по оси x – косинус угла , координата по оси y – синус угла .

Ещё одно замечание.

Синус тупого угла – положительная величина, а косинус – отрицательная.

Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .

Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .

Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Синус, Косинус, Тангенс, Котангенс // Подготовка к ЕГЭ по МатематикеСкачать

Основное тригонометрическое тождество

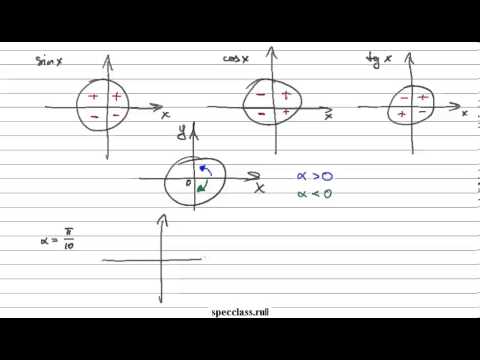
sin 2 α + cos 2 α = 1

Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :

A B 2 + O B 2 = O A 2

sin 2 α + cos 2 α = R 2

sin 2 α + cos 2 α = 1

Видео:Формулы приведения - как их легко выучить!Скачать

Тригонометрия: Таблица значений тригонометрических функций

0 °30 °45 °60 °90 °sin α01 22 23 21cos α13 22 21 20tg α03 313нетctg αнет313 30

Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Тригонометрия: градусы и радианы

Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Тригонометрия: Формулы приведения

Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:

sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °

sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °

sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °

sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °

cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °

cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °

cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °

cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °

Рассмотрим тупой угол β :

Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:

sin ( 180 ° − α ) = sin α

cos ( 180 ° − α ) = − cos α

tg ( 180 ° − α ) = − tg α

ctg ( 180 ° − α ) = − ctg α

Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Тригонометрия: Теорема синусов

В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

a sin ∠ A = b sin ∠ B = c sin ∠ C

Видео:18+ Математика без Ху!ни. Формулы ПриведенияСкачать

Тригонометрия: Расширенная теорема синусов

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R

Видео:Вычисление значений тригонометрических функцийСкачать

Тригонометрия: Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A

b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B

c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C

Видео:Отбор корней по окружностиСкачать

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с тригонометрией.

Видео:Найти знак тригонометрической функции (bezbotvy)Скачать

Тригонометрия: Тригонометрические уравнения

Это тема 10-11 классов.

Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!

Видео:🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Вычисление значений тригонометрических функций с помощью формул приведения и единичной окружности. 10-й класс

Разделы: Математика

Класс: 10

Цели и задачи:

• Образовательная: формирование умений и навыков применения формул приведения и единичной окружности для вычисления значений синуса, косинуса, тангенса углов, использование мнемонического правила для этих формул к преобразованию тригонометрических выражений
• Развивающая: учить анализировать, сравнивать, строить аналогии, обобщать и систематизировать, доказывать и опровергать.
• Воспитательная: воспитание добросовестного отношения к труду и положительного отношения к знаниям.
• Здоровьесберегающая: создание комфортного психологического климата на уроке, атмосферы сотрудничества: ученик – учитель.

Тип урока: комбинированный

Ход урока

I. Организационный момент

“Однажды царь решил выбрать из своих придворных первого помощника. Он подвёл всех к огромному дверному замку. «Кто откроет, тот и будет первым помощником.» Никто не притронулся даже к замку. Лишь один визирь подошёл и толкнул замок, который открылся. Он не был закрыт на ключ.

Тогда царь сказал: «Ты получишь эту должность, потому что полагаешься не только на то, что видишь и слышишь, но надеешься, на собственные силы и не боишься сделать попытку”.

Сегодня на уроке мы будем полагаться не только на то, что видим и слышим, но и на собственные силы и не будем бояться сделать попытку.

II. Повторение табличных значений тригонометрических функций для углов 0°, 30°, 45°, 60°, 90°

Изучая раздел “Тригонометрия” мы часто пользуемся табличными значениями тригонометрических функций для углов 0°, 30°, 45°, 60°, 90°. Давайте их вспомним (слайд)

Но как быть, если какое-нибудь значение забудется? К уроку вам было дано задание найти способ или правило быстрого запоминания этих значений.

“Тригонометрия на ладони” Мнемоническое правило (объясняет ученик) (Слайд 2)

В этом случае нам поможет наша рука. На экране вы видите изображение руки и формулу где n – номер пальца.

Давайте внимательно посмотрим на нашу руку. Если провести линии через мизинец и большой палец, то они пересекутся в точке, называемой “лунный бугор”. Образуется угол 90°. Линия мизинца образует угол 0°. Проведя лучи из “лунного бугра” через безымянный, средний, указательный пальцы, получаем углы соответственно 30°, 45°, 60°. Подставляя вместо n, 0, 1, 2, 3, 4, получаем значения sin, для углов 0°, 30°, 45°, 60°, 90°. Давайте попробуем.

, , , ,

Для cos отсчет происходит в обратном порядке.

III. Этап подготовки учащихся к активному и сознательному усвоению и закреплению материала:

А как вы думаете, можно ли вычислить значения тригонометрических функций для тупых углов? Конечно можно, и в этом нам помогут формулы приведения, которые приводят значения тригонометрических функций остальных углов к значениям тригонометрических функций для острых углов.

Формулами приведения называют формулы, которые сводят значения тригонометрических функций для углов вида к значениям острых углов. (Слайд 3)

На прошлом уроке мы с вами с помощью формул сложения вывели и доказали эти формулы, сейчас вы видите их перед вами.

Формул приведения много, а точнее 32. (Слайд 4) И все формулы надо знать. К счастью существует простое мнемоническое правило, позволяющее быстро воспроизвести любую формулу приведения. Правда для этого надо хорошо знать основы тригонометрии – единичную окружность и способы работы с ней.

IV. Мнемоническое правило

Давайте внимательно посмотрим на эти формулы и выявим сходство и различия в них.

Каждая формула связывает между собой либо синус с косинусом, либо тангенс с котангенсом. Причём, первая функция либо меняется на вторую, либо нет.

В левой части формулы аргумент представляет собой сумму или разность одного из “основных координатных углов”: и острого угла , а в правой части аргумент

В правой части знак перед функцией либо “плюс”, либо “минус”.

Достаточно задать себе два вопроса: (Слайд 5)

1. Меняется ли функция?

Ответ: Если в формуле присутствуют углы или – это углы вертикальной оси (рабочие), киваем головой по вертикали и сами себе отвечаем: “Да”, если же присутствуют углы горизонтальной оси или (спящие), то киваем головой по горизонтали и получаем ответ: “Нет”.

2. Какой знак надо поставить в правой части формулы?

Ответ: Знак определяем по левой части. Смотрим, в какую четверть попадает угол, и вспоминаем, какой знак в этой четверти имеет функция, стоящая в левой части.

Например:

1) “Меняется функция или нет?”

– угол вертикальной оси, киваем головой по вертикали: “Да, меняется”. Значит, в правой части будет cos .

Угол попадает в ІV ч. sin в ІV ч. имеет знак “минус”. Значит, в правой части ставим знак “минус”.

Итак, получили формулу,

Где же применяются формулы приведения?

Одно из применений – нахождение значений тригонометрических функций различных углов с помощью приведения к углу 1-ой четверти.

Решение упражнений с комментированием учащихся с места:

Верна ли запись?

tg

Второе применение – упрощение тригонометрических выражений. Но об этом мы поговорим на следующем уроке.

V. Работа с единичной окружностью

Значения тригонометрических функций для углов больших 90 градусов удобно находить с помощью единичной окружности. (Слайды 7-9) (Комментирует учитель).

VI. Практическая работа

1 вариант проходит к компьютерам и выполняет тест, 2 вариант вычисляет значения тригонометрических функций с помощью единичной окружности. Поднимите руки, у кого за тест 5 и 4. Молодцы, справились с заданием. Теперь поменяйтесь местами.

V. Итог урока:

Сегодня на уроке мы рассмотрели только 3 приёма: быстрого запоминания тригонометрических значений, формул приведения, вычисления тригонометрических функций с помощью единичной окружности. Какой приём вам больше понравился? Применение различных приёмов и способов в математике развивает познавательную деятельность и помогает добиться лучших результатов.

VI. Домашнее задание

С помощью единичной окружности выполнить №155, формул приведения №157 стр. 296.
Спасибо за урок!

🎥 Видео

Синус, косинус произвольного угла. 9 класс.Скачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Таблица значений тригонометрических функций - как её запомнить!!!Скачать

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать