Как найти косинус угла между диагоналями четырехугольника

Сразу скажу, что я не математик, я бы решала так:
Дано:
Четырёхугольник ‘ABCD’, имеющий две диагонали ‘AC’ и ‘BD’, пересекающиеся в точке ‘О’.
Известны все углы у его вершин `ABC`, `BCD`, `CDA`, `DAB` и ещё углы `OAD`, `OAB`, `OCB` и `OCD`.
Нужно найти:
Углы между диагоналями четырёхугольника: т.е., углы ‘АОВ’, ‘АОD’, ‘DOC’, ‘COB’.

Я думаю, что решение данных задач станет возможно, если добавить условие, что в данном четырехугольнике одна пара связанных углов равна между собой.

В таком случае, мой вариант части решения:

Подсказка:
читать дальше Т.к. все диагонали в данном четырехугольнике пересекаются, то мы имеем дело с выпуклым четырехугольником (в противном случае, все диагонали не смогли бы пересечься).
Согласно свойству связанных углов выпуклого четырёхугольника https://mathvox.ru/geometria/mnogougolniki/glava-2-chetirehugolniki-i-ih-svoistva/ugli-vipuklogo-chetirehugolnika-svoistvo-3/ «Если в выпуклом четырёхугольнике одна пара связанных углов равна,
(Например, угол ‘BCA’ = углу ‘BDA’),
то вторая пара связанных углов (‘ABD’ и ‘АСD’) также будут равны между собой.

Если посмотреть на задачу шире, то, углы между диагоналями четырёхугольника (АОВ’, ‘АОD’, ‘DOC’, ‘COB’) ОДНОВРЕМЕННО являются также углами треугольников (‘АОB’, ‘BOC’, ‘COD’, ‘DOA’).
Что мы знаем о треугольниках?
«Сумма ВСЕХ УГЛОВ любого вида треугольников равна 180 градусам».

Поиск угла ‘АОD’
Далее вычислим один из углов диагоналей четырехугольника (он же угол, входящий в состав одного из треугольников) на примере треугольника ‘АOD’:

Сумма всех углов треугольника ‘OAD’ =
угол ‘OAD’ + угол ‘ADO’ + угол ‘AOD’=180 градусов.

По условию задачи мы знаем:
1. Чему равен угол ‘OAD’ (согласно условию задачи).
Неизвестны углы ‘ADO’ и ‘AOD’.

2. Вычисляем угол ‘ADO’:
Снова расширяем своё видение.
Мы знаем:
1. Чему равен угол ‘CDA’ (согласно условию задачи), составной частью которого является угол ‘ADO’.
T. е., угол ‘CDA’ = угол ‘AOD’ + угол ‘ADO’.

2. Вычисляем значение угла ‘АDO’:
Угол ‘АDO’ = углу ‘BDA’.
Согласно свойству связанных углов выпуклого четырёхугольника:
угол ‘BDA’ = углу ‘BCA’, а угол ‘ВСА’ = углу «OCB’.
Т.о., угол ‘ADO’ = углу ‘OCB’ (значение угла ‘OCB’ мы знаем по условию задачи).

3. Угол ‘AOD’ = (угол ‘ОAD’ +угол ‘АDO’) — 180 градусов.
Поздравляем, первый угол ‘АОD’ — найден! .

Поиск угла ‘DOC’
Треугольник ‘DOC’ имеет углы: ‘ОСD’, ‘СDO’ и ‘DOC’.
Мы знаем:
1. Чему равен угол ‘ОСD’ (по условию задачи).

2. Вычислим чему равен угол ‘СDO’:
Угол ‘СDO’ входит в состав угла ‘CDA’, вместе с углом ‘АDO’.
Т.о., угол ‘СDO’ = угол ‘СDA’ — угол ‘АDO’.
3. Вычислим чему равен угол ‘DOC’:
Угол ‘DOC’ = (угол ‘OCD’ + угол ‘CDO’) — 180 градусов.
и т.д.

Видео:Косинус угла между векторами. Коллинеарность векторовСкачать

Творческая работа учащегося «Теорема косинусов для четырёхугольника»

Видео:Угол между векторами | МатематикаСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Муниципальное автономное общеобразовательное учреждение

«Гимназия №1 Октябрьского района г. Саратова»

Научно-практическая конференция школьников.

Теорема косинусов для четырехугольника

Творческая работа ученицы 10 «А» класса

Всем известна теорема косинусов для треугольника

Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними .

Но не все знают, что существуют аналогичные теоремы и для других фигур.

Целью данной работы явилось:

Установить, существует ли теорема косинусов для фигур, отличных от треугольника

Доказать утверждение теоремы косинусов для четырехугольника

Применить теорему при решении задач

Получить полезные следствия из теоремы косинусов для четырехугольника

Теоретическая часть

Первая теорема косинусов

Рассмотрим четырехугольник (рис.1).

Возведем обе части равенства в квадрат

Так как скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними, то для вычисления скалярного произведения векторов будем откладывать векторы от одной точки.

Учитывая также, что скалярный квадрат вектора равен квадрату его длины, получаем:

Заметим, что , где угол, образованный продолжениями сторон .

Введем обозначения сторон четырехугольника (рис.2).

Полученное соотношение между сторонами четырехугольника называют первой теоремой косинусов для четырехугольника. Ее формулируют так:

Квадрат стороны четырехугольника равен сумме квадратов трех других его сторон без удвоенных произведений этих сторон, взятых попарно, и косинусов углов между ними.

Рассмотрим еще раз рис.2. Понятно, что

Тогда равенство теоремы косинусов может быть записано в виде

Теорему косинусов, так как она доказывалась с использованием векторов, можно считать верной и для невыпуклого четырехугольника, и для четырехугольника с самопересечением сторон.

Вторая теорема косинусов

Можно получить еще один аналог теоремы косинусов, который назовем второй теоремой косинусов для четырехугольника.

Рассмотрим четырехугольник с проведенными в нем диагоналями, длины которых обозначим e и f (рис.3А).

Построим вне этого четырехугольника

Ясно, что по двум углам

Составим отношения сходственных сторон

Построим вне этого четырехугольника

Тогда по двум углам.

Составим отношения сходственных сторон:

откуда

Заметим, что имеют равные длины.

Совместим рисунки 3Б и 3В на одном рисунке 4.

Рассмотрим четырехугольник и треугольник .

В четырехугольнике BDEF сумма равна сумме углов треугольника.

В треугольнике сумма всех углов равна 180, поэтому сумма четырехугольника равна 180.

– это односторонние углы при прямых и секущей , а значит, . Кроме того, . Значит, четырехугольник – параллелограмм. И , т.е. равен диагонали f .

Рассмотрим треугольник . Заметим, что равен сумме углов и четырехугольника .

Применим традиционную теорему косинусов к этому треугольнику:

Используя введенные обозначения, получим:

Так как сумма углов выпуклого четырехугольника равна 360,

Значит, в равенстве в качестве множителя + может участвовать и . Тогда вывод из равенства можно сформулировать так:

Квадрат произведения диагоналей четырехугольника равен сумме квадратов произведений противоположных сторон минус удвоенное произведение всех сторон четырехугольника на косинус суммы противоположных углов.

Это соотношение назовем второй теоремой косинусов для четырехугольников. Автором этого соотношения считают немецкого математика 19 века Карла Антона Бретшнайдера .

Получить из второй теоремы косинусов для четырехугольника теорему Птолемея.

Рассмотрим четырехугольник (рис.5), который может быть вписан в окружность. В таком четырехугольнике суммы противоположных углов равны 180. Тогда в равенстве

. И соотношения для диагоналей и сторон четырехугольника принимает вид

Это равенство известно под названием теорема Птолемея :

Для четырехугольника, вписанного в окружность, произведение диагоналей равно сумме произведений противоположных сторон.

Доказать, что в параллелограмме с углом в 45 градусов квадрат произведения диагоналей равен сумме четвертых степеней двух его смежных сторон (рис.6).

c = a , d = b

Задача №3.

Получить из второй теоремы косинусов для четырехугольника теорему Стюарта.

Рассмотрим четырехугольник со сторонами и диагоналями (рис.7).

По теореме косинусов для этого четырехугольника справедливо равенство

Представим себе, что четырехугольник будет таким, что сумма сторон равна диагонали , то есть четырехугольник вырождается в треугольник (рис.8), то есть

Вычисляем по теореме косинусов для треугольника, получаем,

Тогда для этого вырожденного четырехугольника имеем

Полученное соотношение называется теоремой М. Стюарта.

Получить из теоремы Стюарта формулу длины медианы треугольника.

Решение.

Квадрат медианы равен четверти суммы удвоенных квадратов сторон треугольника, заключающих медиану, минус квадрат третьей стороны треугольника.

Получить из теоремы Стюарта формулу длины биссектрисы треугольника.

Если – биссектриса, то по свойству биссектрис в треугольнике

Квадрат биссектрисы треугольника равен разности произведений сторон треугольника, заключающих биссектрису, и отрезков противоположной стороны, на которые она разделена биссектрисой.

В данной работе получены следующие результаты:

сформулированы и доказаны две теоремы косинусов для четырехугольника;

с использованием доказанной теоремы доказана теорема Птолемея;

доказана теорема Стюарта;

получены два следствия из теоремы Стюарта: формула длины медианы и формула длины биссектрисы;

приведен пример использования теоремы косинусов для четырехугольника при решении задач.

Атанасян Л.С. ГЕОМЕТРИЯ. 7-9 кл. Москва, Издательство «Просвещение», 2006г.

Атанасян Л.С. ГЕОМЕТРИЯ. 10-11 кл. Москва, Издательство «Просвещение», 2006г.

Понарин Я.П. Элементарная геометрия в 3-х томах. Том 1. Планиметрия, преобразования плоскости. Москва, Издательство МЦНМО, 2004г.

Единая коллекция цифровых образовательных ресурсов https://school-collection.edu.ru

Видео:Вычисляем угол через координаты вершинСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 967 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 340 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 691 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Гришина Ирина ВладимировнаНаписать 1671 15.07.2017

Номер материала: ДБ-603154

15.07.2017 2165

15.07.2017 648

15.07.2017 386

15.07.2017 827

15.07.2017 571

15.07.2017 177

15.07.2017 770

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

Названы главные риски для детей на зимних каникулах

Время чтения: 3 минуты

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Число участников РДШ за 2021 год выросло в три раза

Время чтения: 2 минуты

ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📹 Видео

Найдите длины диагоналей параллелограмма, построенного на векторах a=(1;-1;-4) и b=(-5;3;8)Скачать

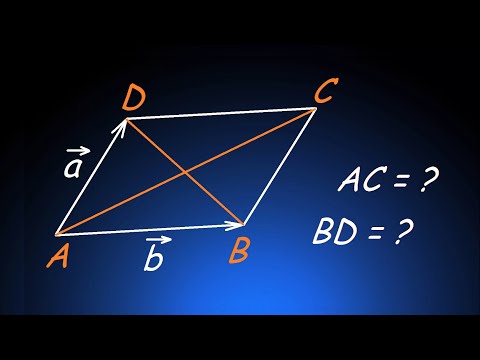
18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Нахождение угла между векторами через координаты. 9 класс.Скачать

Задача 3. Найти косинус угла между векторами.Скачать

Как находить угол между векторамиСкачать

ОГЭ как найти тангенс угла, если нет треугольника #математика #огэ #огэматематика #геометрияСкачать

Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Угол между векторами. 9 класс.Скачать

Найти угол между векторами и площадь параллелограмма, построенного на этих векторахСкачать

Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэСкачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

11 класс, 5 урок, Угол между векторамиСкачать

Площадь параллелограмма, построенного на данных векторахСкачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

ОГЭ по математике. Площадь четырехугольника можно вычислить по формуле (вар. 5)Скачать

Скалярное произведение векторов. 9 класс.Скачать