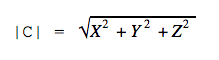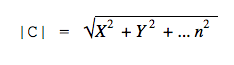Как вычислить корень из вектора (4 видео)

Операции с векторами

Как сложить и перемножить векторы (и зачем).

Мы постепенно показываем вам математику за пределами школьной программы. Начинали со знакомства с векторами, теперь сделаем следующий шаг.

Напомним основные мысли:

Вектор — это абстрактное понятие, которое представляет собой организованную последовательность каких-то чисел.
В виде вектора можно представить координаты предмета в каком-то пространстве; площадь квартиры и её стоимость; цифровые данные анкеты какого-то человека и динамику цен на нефть.
Если по-простому, то векторы нужны, чтобы обрабатывать большое количество организованных чисел. Представьте, что вектор — это коробка с конфетами, только вместо конфет — числа. Каждое число стоит в своей ячейке.
Машинное обучение основано на перемножении матриц, которые, в свою очередь, можно представить как наборы векторов. Так что векторы лежат в глубине всех модных и молодёжных технологий ИИ.

С векторами можно совершать некоторые математические операции. Вот о них и поговорим.

Содержание

Правильно — векторы
Сложение
Интуитивное изображение сложения
Вычитание
Длина вектора
Умножение и деление вектора на число
Да вроде несложно!
Что дальше
Как я отказался от вычисления квадратного корня
Как найти длину вектора
Формула
Примеры вычисления длины вектора
🔍 Видео

Видео:Как считать корни? #shortsСкачать

Правильно — векторы

Математики часто говорят во множественном числе «вектора», но по словарю правильно «векторы». Это такой профессиональный жаргон, как «договора», «бухгалтера» и «сервера». Мы будем использовать «векторы», но если вы окажетесь в постковидном математическом баре, лучше говорите «вектора».

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Сложение

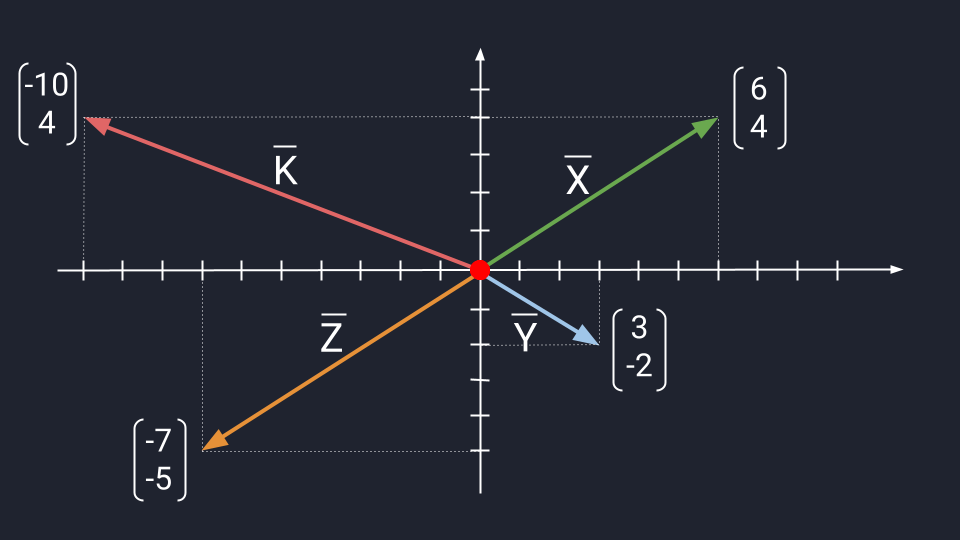
Представим четыре вектора, которые лежат в двухмерном пространстве и пока что не связаны между собой. Нарисуем эти векторы и обозначим их буквами X, Y, Z, K.

Поскольку векторы находятся в одном пространстве, координаты каждого состоят из одинакового количества чисел. У нас пример с двухмерным пространством и два числа. Выглядеть это будет так: X = (6, 4); Y = (3, −2); Z = (−7, −5); K = (−10, 4).

Векторы X, Y, Z, K в двухмерном пространстве

Если у нас несколько векторов с одинаковым количеством чисел, то эти числа можно поэлементно складывать. Для этого мы берём первое число одного вектора, складываем его с первым числом другого вектора и так далее.

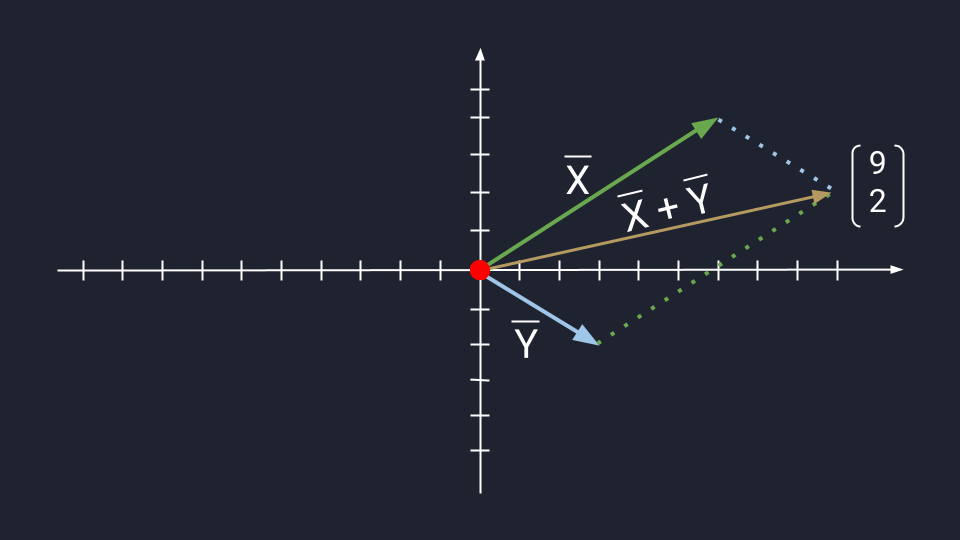
Предположим, нам нужно сложить векторы X и Y.

X = (6, 4)
Y = (3, −2)
X + Y = (9, 2)

Вроде просто: складываешь последовательно все координаты, результаты сложения складываешь в исходные коробочки. Так можно делать с любым количеством координат. Помните, что вектор — это необязательно стрелка в двумерном пространстве. Она может быть и в десятимерном пространстве — с точки зрения математики это неважно.

Например, вот сложение векторов с пятью координатами:

X = (6, 4, 11, 14, 99)
Y = (3, -2, 10, -10, 1)
X + Y = (9, 2, 21, 4, 100)

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Интуитивное изображение сложения

Для интуитивного восприятия удобно использовать векторы с двумя координатами. Их удобно рисовать на координатной плоскости и таким образом смотреть на геометрию.

Например, можно на плоскости показать, как будет работать сложение двух векторов. Для этого есть два метода: метод треугольника и метод параллелограмма.

Метод треугольника: ставим векторы Х и Y в очередь друг за другом. Для этого берём вектор Х, ставим за ним вектор Y и получаем новый вектор. Новый вектор начинается в хвосте вектора Х и заканчивается на стрелке вектора Y. Этот вектор — результат сложения. Представьте, что это ребёночек двух векторов.

Сложение векторов по методу треугольника: X = (6, 4); Y = (3, −2); Х + Y = (9, 2)

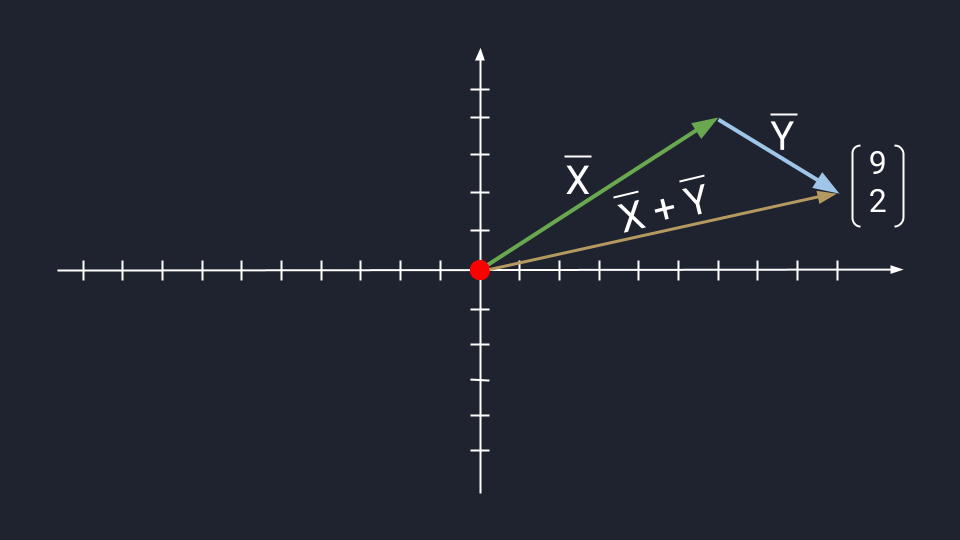
Чтобы воспользоваться методом параллелограмма, нам нужно поставить векторы Х и Y в одну исходную точку. Дальше мы дублируем векторы Х и Y, формируем параллелограмм и получаем новый вектор. В новом векторе соединяем исходную точку с исходной точкой дублирующих векторов — стрелка проходит посередине параллелограмма. Длина нового вектора — это сумма векторов Х и Y.

Сложение по методу параллелограмма и треугольника даёт одинаковый результат. Поэтому выбирайте вариант, который больше подходит под задачу.

Сложение векторов по методу параллелограмма: X = (6, 4); Y = (3, -2); Х + Y = (9, 2)

Видео:Как вычислить любой неизвлекаемый кореньСкачать

Вычитание

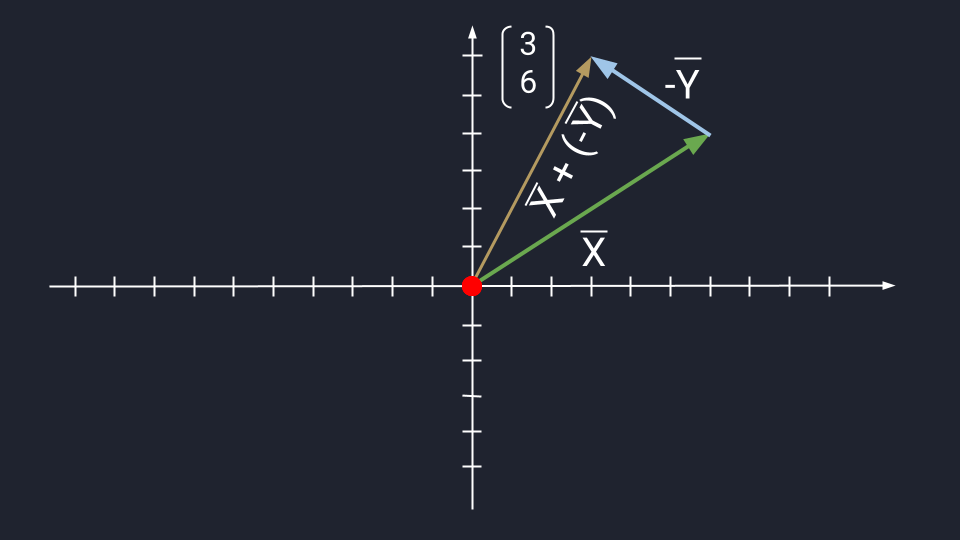
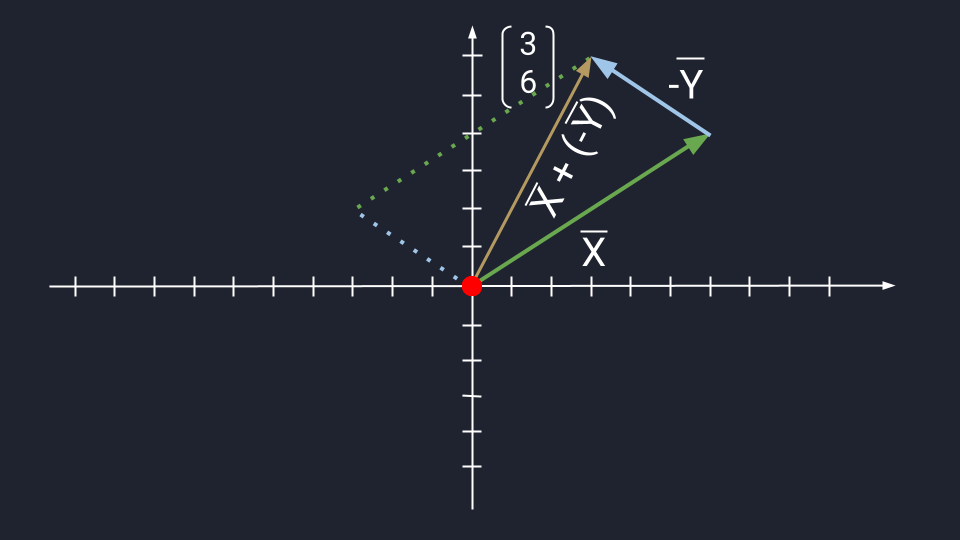
Вычитание векторов немного сложнее. Чтобы вычесть векторы, нужно «развернуть» вычитаемый вектор и сложить его с исходным. «Развернуть» — то есть направить в обратную сторону, «перевернув» знаки координат. Получится конструкция вроде такой: Х + (−Y)

Дальше используются правила сложения. Пошагово это выглядит так:

У нас есть X = (6, 4) и Y = (3, −2).
Превращаем формулу Х − Y в формулу Х + (−Y).
Разворачиваем вектор Y. Было: Y = (3, −2). Стало: −Y = (−3, 2).
Считаем: X + (−Y) = (3, 6).

Теперь посмотрим, как выглядит вычитание векторов на графике:

Вычитание векторов по методу треугольника: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6) Вычитание векторов по методу параллелограмма: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6)

Видео:Собственные векторы и собственные значения матрицыСкачать

Длина вектора

Длина вектора — это одно число, которое измеряется расстоянием от кончика до стрелки вектора. Длину вектора нельзя путать с координатами. Координаты — это несколько чисел, которые указывают на расположение стрелки вектора. По координатам можно определить только конечную точку вектора. Например, если X = (6, 2), то стрелка будет находиться в точке 6 по оси Х. Или другой пример: если Y = (6, 5), то стрелка этого вектора будет находиться в точке 5 по оси Y.

Предположим, нам известны начальные точки векторов X и Y. Пусть это будет точка 2 по оси X и точка 2 по оси Y. Так мы можем легко посчитать длину отрезков:

X = 6 − 2 = 4
Y = 5 − 2 = 3

Иногда приходится рассчитывать длину третьего вектора, который привязан к двум другим векторам. Это легко сделать с помощью теоремы Пифагора — это когда квадрат гипотенузы равен сумме квадратов катетов. В нашем случае катетами будут длины векторов X и Y. Вспоминаем школьную формулу и считаем:

|C|2 = 42 + 32 = 25
|C| = √25 = 5 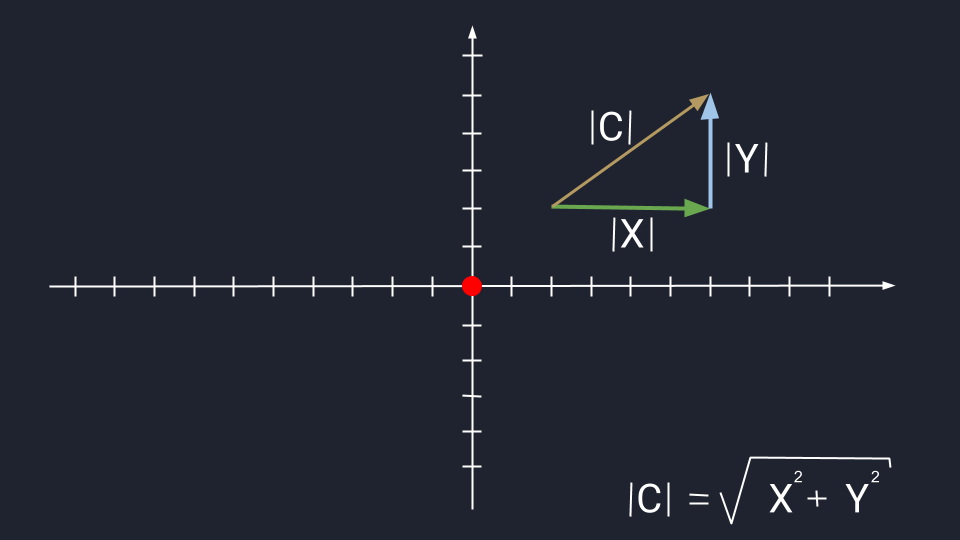Длина вектора считается по формуле прямоугольного треугольника. Чтобы было проще представить — перенесите векторы на систему координат

Это формула для двумерного пространства. В трёхмерном пространстве формула похожая: нужно сложить квадраты трёх координат и вычислить квадратный корень из суммы.

В пространстве с большим числом измерений формула выглядит сложнее, но по сути то же: складываем все квадраты координат и получаем квадратный корень из этой суммы.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Умножение и деление вектора на число

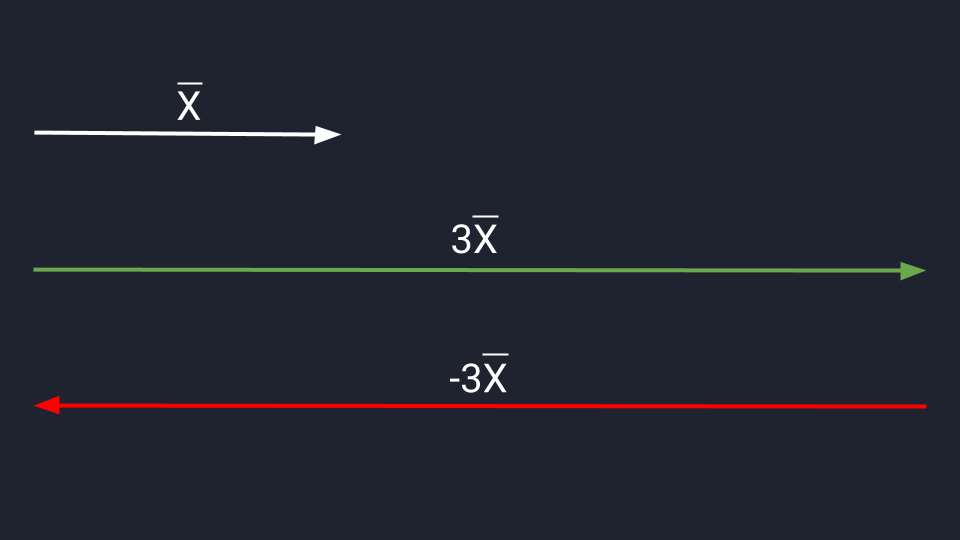
Умножение и деление позволяют изменить длину и направление вектора. Если мы умножим вектор Х на три, то увеличим его длину в три раза. Если умножим на минус три — увеличим длину и изменим его направление на противоположное.

Умножение вектора на число

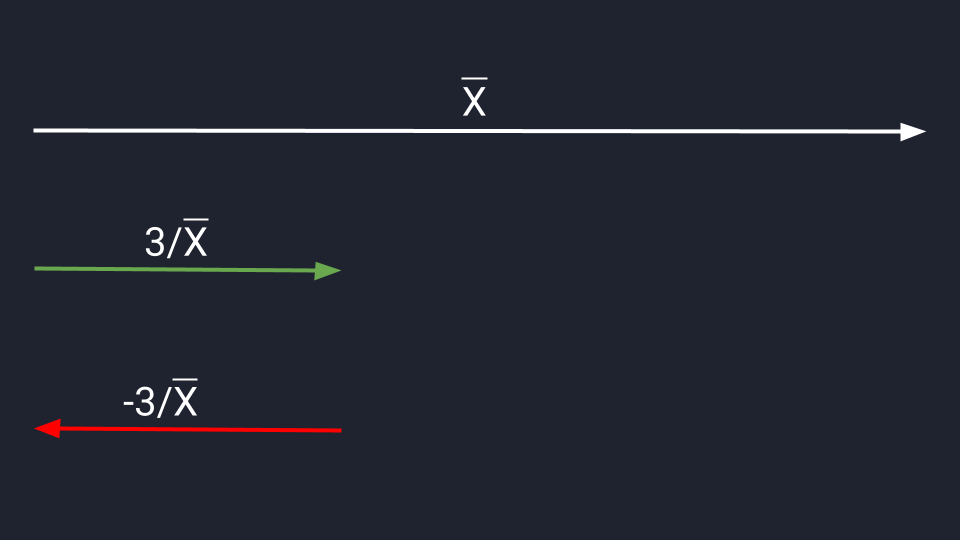
Для деления сохраняются аналогичные правила. Делим вектор Х на три и сокращаем длину в три раза. Делим на минус три — сокращаем и разворачиваем.

Деление вектора на число

Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Да вроде несложно!

Пока ничего сложного. Но если углубляться, вы узнаете, что:

векторы можно умножать на векторы тремя способами в зависимости от задачи и от того, что мы понимаем под умножением;
если от векторов перейти к матрицам, то перемножение матриц имеет несколько более сложную и довольно неинтуитивную математику;
а перемножение матриц — это и есть машинное обучение.

Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать

Что дальше

В следующей статье рассмотрим линейную зависимость векторов. Чтобы не скучать — посмотрите интервью с Анастасией Никулиной. Анастасия сеньор-дата-сайентист в Росбанке и по совместительству блогер с интересной историей.

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Как я отказался от вычисления квадратного корня

Очень часто при цифровой обработке сигналов необходимо вычислить длину вектора, обычно это делается по формуле A=SQRТ(X^2+Y^2). Здесь возвести в квадрат значение не сложно, но операция вычисления квадратного корня не является простой операцией, особенно для микроконтроллеров. Кроме того, алгоритмы вычисления корня выполняются не стабильное время, и для алгоритмов, в которых таких вычислений много, становится сложно прогнозировать время, необходимое для вычислений.

С такой задачей столкнулся и я. О том, как я отказался от процедуры вычисления корня, читайте ниже.

Для начала рассмотрим четыре вектора, они лежат в разных четвертях.

Сведем все в одну четверть — в первую. Для этого возьмем координату Y и если она отрицательная, то превратим ее в положительную. В случае если она и так положительная, то оставим все без изменений.

На самом деле, поскольку у меня абсолютные координаты и значения указаны в целых числах без знака, то вычислим модуль.

Если Y>2047, то Y=Y-2047
Если Y 2047, то X=X-2047
Если X X, то угол вектора лежит в области 45-90 градусов, а если Y X, то TEMP=Y, Y=X, X=TEMP (меняем X и Y местами).
Если Y Таблица

Младшее значение 0x800h, что означает 2048. Cтаршее 0xB50, и оно означает 2896.
2896/2048 = 1.414, что соответствует 1/cos(45).

Для получения индекса массива необходимо умножить Y на 2048 и разделить на Х.

Полученный индекс укажет на ячейку массива, из этой ячейки извлекаем значение, умножаем X на него и делим на 2048. Полученный результат есть длина вектора.

Хочу заметить, что деление и умножение на 2048 выполняется сдвигом, и еще одно деление и умножение выполняется специальными командами или алгоритмами, если в используемой платформе нет команд умножения и/или деления.

В моем случае применялся микроконтроллер STM32F103, который имел команды деления и умножения.

Подведем итог алгоритма.

Проверка знака по Y и разворот, если необходимо.
Проверка знака по X и разворот, если необходимо.
Сравнение X и Y и обмен местами, если необходимо.
Проверка X на 0.
Умножение Y на 2048 сдвигом.
Деление Y на X.
Прибавляем полученное значение к адресу массива и читаем значение K.
Умножаем X на K.
Делим X на 2048 сдвигом.

Получившаяся программа на языке ассемблер для STM32F103.

Приведу пример работы алгоритма в сравнении с классическим методом для двух из четырех векторов, которые показаны на изображениях выше.

Возьмем синий вектор (из третьей области).

Его координаты X=-45,Y=-126 (можно проверить по пикселям)

(-45)^2+(-126)^2=2025+15876=17901
SQRT(17901)=133 (усечено до целого)

пункт 1: 2002>2047? -> нет. X=2047-2002=45
пункт 2: 1921>2047? -> нет. Y=2047-1921=126
пункт 3: 126>45 -> да. меняем местами X=126, Y=45
пункт 4: X=0 -> нет. продолжаем
пункт 5: Y=Y*2048, Y=45*2048=92160
пункт 6: I=Y/X, I=92160/126=731
Пункт 7: в таблице 255 строк по 8 значений, ищем 731е значение.
Это 91я строка и 3е значение, которое равно 0x087e, или 2174 в десятичном
виде.
Пункт 8: X=X*2174, X=126*2174=273924
Пункт 9: A=X/2048, A=273924/2048=133 (усечено до целого)

Теперь возьмем зеленый вектор (из четвертой области).

Его координаты X=-170,Y=95 (можно проверить по пикселям).

(-170)^2+(95)^2=28900+9025=37925
SQRT(37925)=194 (усечено до целого)

пункт 1: 1877>2047? -> нет. X=2047-1877=170
пункт 2: 2142>2047? -> да. Y=2142-2047=95
пункт 3: 95>170 -> нет. оставляем как есть.
пункт 4: X=0 -> нет. продолжаем
пункт 5: Y=Y*2048, Y=95*2048=194560
пункт 6: I=Y/X, I=194560/170=1144
Пункт 7: в таблице ищем 1144е значение.
Это 143я строка и 0е значение, которое равно 0x092A, или 2346 в десятичном виде.
Пункт 8: X=X*2346, X=170*2346=398820
Пункт 9: A=X/2048, A=398820/2048=194 (усечено до целого)

Подобный алгоритм можно использовать в ЦОС (как я), например, можно заметно ускорить Быстрое Преобразование Фурье. Также можно использовать в компьютерной графике, где используется трассировка лучей. Возможно и еще есть применение.

Видео:#140. КАК ИЗВЛЕКАТЬ КОРНИ В СТОЛБИК? В ШКОЛЕ НЕ ПОКАЖУТ!Скачать

Как найти длину вектора

Видео:Угол между векторами | МатематикаСкачать

Формула

Чтобы найти длину вектора, заданного своими координатами, нужно извлечь корень квадратный из суммы квадратов его координат. Если вектор задан на плоскости и имеет координаты $bar=left(a_ ; a_right)$, его длина вычисляется по формуле:

Видео:Статика #2. Подготовка к ВсОШ по физикеСкачать