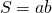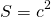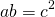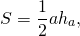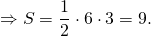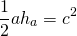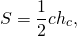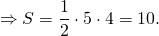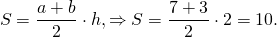Как в окружность вписать прямоугольник равновеликий данному квадрату (7 видео)

Равновеликие фигуры

Равновеликие фигуры — это фигуры, которые имеют одинаковые площади.

Равновеликие тела — это тела, которые имеют равные объёмы (равновеликие тела часто также называют равновеликими фигурами). Равные фигуры — это фигуры, которые совпадают при наложении (у них соответствующие стороны равны и соответствующие углы равны).

Равные фигуры имеют равные площади, поэтому равные фигуры являются также равновеликими. Обратное, вообще говоря, неверно.

Примеры равновеликих фигур .

1) Прямоугольник и квадрат, изображенные на рисунке 1, — равновеликие фигуры.

То есть, прямоугольник со сторонами a и b и квадрат со стороной c являются равновеликими, если

2) Треугольник и квадрат, изображенные на рисунке 2 — равновеликие фигуры, так как имеют равные площади.

Площадь квадрата S=3²=9.

Треугольник со стороной a и проведенной к ней высоте ha и квадрат со стороной c являются равновеликими, если

3) Треугольник и трапеция, изображенные на рисунке 3 — равновеликие, поскольку их площади равны.

Треугольник со стороной c и проведенной к ней высотой hс и трапеция с основаниями a и b и высотой h являются равновеликими, если

Содержание

Методическое пособие «Решение геометрических задач аналитическим способом»
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Алгебраический метод
🎬 Видео

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Методическое пособие «Решение геометрических задач аналитическим способом»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Задача.Окружность и прямоугольник вписаны в квадрат.Скачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

по теме: «Решение геометрических задач аналитическим способом»

АНАЛИТИЧЕСКИЙ МЕТОД РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ

Уравнения первой и второй степени

Алгебраические преобразования. Тождества и неравенства

Тригонометрические тождества и уравнения

Уравнения и неравенства смешанного вида

Задачи на построение

Задачи на отыскание наибольших и наименьших значений

Зависимости между элементами треугольника

Зависимости между элементами четырехугольника

Зависимости между элементами тетраэдра

Решение задач по математике имеет большое общеобразовательное и воспитательное значение. Процесс решения задачи представляет собой поиск выхода из затруднения или пути обхода препятствия, — это процесс достижения цели, которая первоначально не кажется сразу доступной [7]. Решение задач является специфической особенностью интеллекта, а интеллект – это особый дар человека; поэтому решение задач может рассматриваться как одно из самых характерных проявлений человеческой деятельности [11]. Поиск решения нестандартной задачи развивает инициативу, настойчивость и сообразительность.

Сборник: «Решение геометрических задач аналитическим способом» рассчитан на то, чтобы показать рациональность применения аналитического способа при решении геометрических задач во время подготовки к выпускным экзаменам, тестированию.

1 АНАЛИТИЧЕСКИЙ СПОСОБ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ.

Уравнения первой и второй степеней.

В начале приведем примеры задач по геометрии, приводимые к алгебраическим уравнениям первой и второй степени.

Для решения таких задач следует сделать чертеж и составить уравнение, выражающие связь между данными и неизвестными элементами фигуры [6].

Пример 1. Длины боковых сторон трапеции равны 3 и 5. известно, что в трапецию можно вписать окружность. Средняя линия трапеции делит ее на две части, отношение площадей которых равно 5/11.

Найти длины оснований трапеции [9].

Обозначим ВС=х, AD =у, т.к. в четырехугольник ABCD можно вписать окружность, то х+у= BC + AD = AB + CD =8. Поскольку KL — средняя линия трапеции, то из теоремы о пропорциональных отрезках отсекаемых параллельными прямыми, следует, что высоты трапеций KBCL и AKLD равны h /2. Для площадей этих трапеций имеем

Алгебраические преобразования. Тождества и неравенства.

Часто в повседневной жизни мы можем услышать, что кто-то купил новую вещь, совершил какую-либо глупость, употребил грубое выражение и многое другое. Но это всего лишь слухи, а так ли это на самом деле задумывается не каждый. Тот, кто воспринимает этот слух всерьез, имеет перед собой готовую «задачу на доказательство»: ему предстоит снять со слуха покров сомнения, он должен доказать (или опровергнуть), что данное действие было совершено, и это доказательство или опровержение должно быть им мотивировано со всей доступной в данном случае убедительностью. Когда мы встречаемся с математической задачей на доказательство, нам предстоит снять сомнение в правильности четко сформулированного математического утверждения — мы должны доказать или опровергнуть его.

При решении задач на доказательство находят применение тождества и неравенства, известные из школьного курса алгебры. Некоторые задачи могут быть решены способом составления уравнений [3] .

Пример 2. Дан треугольник ABC , в котором АВВС. Доказать, что биссектриса угла В лежит между медианой и высотой, проведенными из той же вершины В [4].

Пусть BC = a , AC = b и AB =с (с≠а)

Если угол С – тупой, то основание высоты BD лежит на продолжении стороны AC и значит AD > b > AF . В этом случае AD > AF > AM , т.е. биссектриса BF лежит между медианой BM и высотой BD .

Пусть С – острый угол, найдем AD . Пусть AD= x . Из ∆ ABD ; имеем: BD 2 = AB 2 — AD 2 , BD 2 = BC 2 — DC 2 , откуда c 2 -x 2 =a 2 -(b-x) 2 . . Покажем, что:

D> AF , т.е. . Рассмотрим разность: .

Т.к. c > a и с+ a > b , то разность положительна. Отсюда AD > AF . Итак, AD > AF > AM , биссектриса BF лежит между медианой BM и высотой BD .

Тригонометрические тождества и уравнения.

Тригонометрические функции находят применение при решении самых разнообразных задач. Существуют задачи, приводимые к тригонометрическим уравнениям, а так же задачи, решаемые путем введения вспомогательных неизвестных. При решении задачи аналитическим методом не требуется остроумных вспомогательных построений, задача сводиться к применению формул, решено уравнение, доказательству тождеств.

Пример 3. В равнобочной трапеции основание AD равно диагонали AC . Известно, что CAD = CDM , где М – середина ВС. Найти углы трапеции [5].

Дано: ABCD – равнобедренная трапеция; AD = AC ; M – середина ВС; CAD = CDA

Найти: BAD , ABC

Пусть CAD = φ , тогда ADC = ACD =90 0 — φ /2. Поскольку по условию MDC = CAD = φ , то CMD = MDA = ADC — MDC =90 0 -3/2 φ , MCD =90 0 + φ /2. По теореме синусов для треугольника MCD найдем:

Но М – середина ВС следовательно, проекция MD на , т.е. .

Из равнобедренного треугольника ACD найдем .

Приравняем:

Таким образом:;

Ответ: ,

Уравнения и неравенства смешанного вида.

Геометрические задачи на вычисление углов иногда приводят к уравнениям более сложного вида, чем тригонометрические уравнения. Например, одна из частей уравнения может быть линейной функцией неизвестного угла, а другая – тригонометрической функцией того же угла. Уравнения такого вида могут быть решены приближенно графическим методом и методом проб. Иногда целесообразно пользоваться обоими способами [2] .

Пример 4. В прямоугольном треугольнике ABC катет AB равен 3, катет АС равен 6. Центры окружностей радиусов 1,2 и 3 находятся соответственно в точках А, В, С. Найти радиус окружности, касающийся каждой из трех данных окружностей внешним образом [4].

Дано:,

Сделаем скелетный чертеж. Нам достаточно провести отрезки OA , OB , OC , где О – центр искомой окружности. Если радиус четвертой окружности равен х, то АО=1+х, ОВ=2+х, ОС=3+х. Введем еще одно неизвестное: , тогда .

Запишем теорему косинусов для треугольников АОС и АОВ. Получим систему уравнений:

Выразим из первого уравнения , а из второго

Используем соотношения

Ответ:

Задачи на построение.

Алгебра и тригонометрия находят применение не только при решении задач на вычисление и на доказательство, но и при решении задач на построение. Задачи на построение являются традиционными задачами в курсе геометрии. Разработкой методов решения этих задач математики занимаются еще со времени Древней Греции [1].

Задачей является непосредственное применение алгебраического метода к геометрическим построениям. Простейшие примеры такого применения изучают еще в школьном курсе геометрии. Так, каждый из нас знает, что построение четвертого пропорционального к трем данным отрезкам выражается формулой . Со школы, знаем построение, дающее отрезок , т.е. среднее пропорциональное двух данных отрезов. Умеем строить гипотенузу с прямоугольного треугольника по данным его катетам, т.е. выполнять «построение» для формулы . Умеем построить катет прямоугольного треугольника по данным гипотенузе и другому катету, что соответствует формуле и т.п. Все эти простейшие построения должны быть хорошо известны, т.к. в конечном счете, именно к ним сводится всякое более сложное применение алгебраического метода [12].

Пример 5. В данную окружность вписать прямоугольник, равновеликий данному квадрату [12].

АНАЛИЗ: пусть в окружность вписан прямоугольник ABCD , равновеликий квадрату со стороной а. Диагональ АС прямоугольника можно построить: она является диаметром окружности; треугольники АВС и ACD конгруэнтны, задача будет решена, если удастся построить точку В, а для этого достаточно построить высоту BH треугольника АВС.

Пусть АС=α и ВН= х. Выразим площадь прямоугольника ABCD через α и х, приравняв её площади данного квадрата, получим уравнение αх=а 2 , откуда х=а 2 /α.

ИССЛЕДОВАНИЕ. Задача имеет решение тогда и только тогда, когда х=а 2 /α, а это равносильно условию (диаметр окружности не меньше диагонали данного квадрата).

ПОСТРОЕНИЕ. В начале построим отрезок ВН, пользуясь полученной формулой . Для этого проведем диаметр АС данной окружности и на окружности построим точку М, так, чтобы АМ=а. Тогда получим: перпендикуляр МЕ к диаметру АС. Тогда получим: . После чего остается на расстоянии х которая пересечет окружность в точке В, и построить точку D симметричную В относительно центра окружности.

ДОКАЗАТЕЛЬСТВО. Т.к. АС и BD – диаметры окружности, то ABCD – прямоугольник. Площадь S прямоугольника равна площади квадрата со стороной а, действительно, .

Легко убедиться в том, что если за неизвестное х принять длину стороны прямоугольника, то формула, выражающая х через длины данных отрезков, окажется громоздкой, и для решения задачи придется выполнить более сложные построения. Таким образом, выбор неизвестных при решении задачи алгебраическим методом имеет существенное значение.

Задачи на отыскание наибольших и наименьших значений.

Задачи на максимум и минимум могут быть также решены элементарными средствами, без использования производной. Одни из них сводятся к нахождению наибольшего или наименьшего значения квадратного трехчлена, другие – к исследованию выражении, содержащего тригонометрические функции.

Хорошо известно, что решение «экстремальных» задач, независимо от того, ч то относятся ли они к арифметике, алгебре, геометрии или математическому анализу, могут строиться двумя принципиально различными путями. Прямым называется такое доказательство какого-либо экстремального свойства, в котором, скажем, определяется фигура непосредственно сравнивается с производной другой фигурой, удовлетворяющей всем условиям поставленной задачи, и оказывается, что первая фигура лучше (или не хуже) каждой другой. Напротив, косвенное доказательство сводиться к рассуждению, показывающему, что все фигуры, кроме какой-то одной (или нескольких), не могут служить решением задачи, поскольку для каждой такой фигуры можно найти другую лучшую, чем она, откуда уже и делается вывод о том, что решение задачи является та единственная фигура, которую мы не можем «улучшить» [3].

Пример 6. Периметр треугольника ABC равен 2р. Какое наибольшее значение может иметь длина заключенного внутри треугольника и параллельного ВС отрезка касательной к вписанной в АВС окружности? Для какого треугольника (каких треугольников) достигается это значение [13]?

Пусть вписанная окружность S треугольника касается его сторон ВС ,АС и АВ длин а, в и с в точках D , Е и F , а прямой KL (где ) — в точке М. Из равенства длин касательных, проведенных из одной точки, следует, что и

Таким образом, периметр 2Р треугольника ALK равен:

Из ∆ABC

, где

Таким образом, наибольшее возможное значение длины m отрезка KL достигается для всех треугольников ABC с основанием

(т.е. в+с=3а); это значение равно

Ответ: для треугольников с основанием .

Зависимости между элементами треугольника.

Среди задач по геометрии встречаются задачи, касающиеся треугольников. Здесь используются теоремы синусов и косинусов, а также формулы, выражающие элементы треугольника через его стороны [5].

Пример 7. В равнобедренном треугольнике KLM длина основания КМ равна а, а длина высоты, опущенной из точки К на боковую сторону ML , равна h . Найти длины всех медиан треугольника [6].

Дано ∆ KLM , KL = LM , KM =а, KP = h , LR = RM , KQ = QM

Рассмотрим ∆ KPM ,

. N — точка пересечений медиан
Откуда

Ответ:

Зависимости между элементами четырехугольника.

Решения их можно получить средствами алгебры и тригонометрии. В некоторых случаях полезно прибегать к вспомогательным построениям, именно с помощью них порой можно очень быстро увидеть правильный путь к получению результата.

Пример 8. В окружность вписан четырехугольник ABCD , диагонали которого взаимно перпендикулярны и пересекаются в точке Е. Прямая, проходит через точку Е и перпендикулярная к АВ, пересекает сторону CD в точке М. доказать, что ЕМ – медиана треугольника CED , и найти ее длину, если AD =8см, АВ=4см и CDB = [2].

Дано: AD =8см; АВ=4см; CDB =

Обозначим через К точку пересечения прямых АВ и ЕМ. Поскольку углы CDB и CA B опираются на одну дугу, то . Из равенства, что это означает, что — равнобедренный, т.е.

Итак, — равнобедренный DM = EM . Доказано, что СМ= DM или, что ЕМ – медиана. Из . Из

Ответ:

Зависимости между элементами тетраэдра.

Рассмотрим метрические соотношения между элементами тетраэдра (произвольной треугольной пирамиды – простейшего из всех многогранников, играющего в стереометрии ту же роль, какую в планиметрии играет треугольник). Что же касается свойств тетраэдра, иногда они в точности аналогичны свойствам плоского треугольника, а иногда своеобразно преломляют известные из планиметрии факты [8].

Пример 9. Ребра равногранного тетраэдра равны а, в и с. Вычислите его объем V и радиус R описанной сферы [10].

Решение: Достроим данный тетраэдр до прямоугольного параллелепипеда; пусть x, y и z – ребра этого параллелепипеда. Тогда и

Так как , где — диагональ параллелепипеда, а , то

Следовательно равенства и и вычитая из них равенство , получаем

Аналогично находим и . Так как объем тетраэдра в три раза меньше объема параллелепипеда, то

Ответ: ;

Таким образом, применение дополнительного построения позволяет упростить решение задачи.

Александров А.Д., Вернер А.А., Рыжик В.И. Геометрия. – М.: просвещение, 1995

Владимиров Ю.Н., Королько Е.А., Фролова И.В. Математика. Учебное пособие для абитуриентов, — 2-е изд., исправ. – Новосибирск: НГУЭУ, 2006. – 192 с.

Готман Э.Г., Сконец З.А. Решение геометрических задач аналитическим методом. – М.: Просвещение, 1979

Дополнение к сборнику заданий для проведения письменного экзамена по математике за курс 11-летней школы с углубленным изучением математики (геометрии).

Жарыгин И.Ф. Факультативный курс по математике / учеб. Пособие для 10 класса средней школы /. – М.: 1989

Методическое пособие по математике для поступающих в Московский институт стали и сплавов. – М.: 1970

Пойа Д. Математическое открытие. – М.: Наука, 1976

Прасолов В.В., Шарыгин И.Ф. Задачи по стереометрии. – М.: Наука, 1989

Сборник тестов по математике./Учебно-методическое пособие. Астана: РГКП «Национальный центр государственных стандартов образования и тестирования», 2012. – 251 с.

Сборник тестов по математике./Учебно-методическое пособие. Астана: РГКП «Национальный центр государственных стандартов образования и тестирования», 2012. – 224 с.

Фридман Л.М., Турецкий Е.Н. Как научится решать задачи. – М.: просвещение, 1984

Четверухин Н.Ф. Методы геометрических построений: Учпедку -1952

Шклярский Д.О., Ченцов Н.Н., Яглом И.М. Геометрические неравенства и задачи на максимум и минимум. М: Наука, 1970

Видео:Задача.Окружность и прямоугольник вписаны в квадрат.Скачать

Алгебраический метод

9.2. Данный отрезок разделить на две части, относящиеся как V2 : 7з.
9.3. Дан отрезок единичной длины. Построить отрезки длиной 7п, где п — натуральное число.
9.4. Построить точку М внутри треугольника АВС, такую что расстояния от М до сторон АВ, ВС и СА относятся как 1:2:3.
9.5. Построить точку М, расстояния от которой до данных точек А, В и С относятся как 1:2:3.
9.6. В данный круг вписать прямоугольник, равновеликий данному квадрату.
9.7. В данный круг вписать прямоугольник данного периметра.
9.8. Провести прямую, которая одновременно делит пополам площадь и периметр данного треугольника.
9.9. Через две данные точки провести окружность, касательную к данной прямой.
9.10. Построить треугольник, равновеликий данному и имеющий то же основание, одна из сторон которого имеет данную длину.
9.11. Построить отрезки, длины которых выражаются абсолютными величинами корней квадратного уравнения: a) x 2 + px + q 2 — 0; б) х 2 — рх — q 2 = 0, где р > 0, q > 0.
9.12. Построить прямоугольный треугольник по гипотенузе с и биссектрисе (З_с.
9.13. В данный квадрат со стороной а вписать квадрат со стороной Ъ так, чтобы только одна его вершина лежала на стороне данного квадрата.
9.14. Построить квадрат, равновеликий данному треугольнику.
9.15. Построить равнобедренный прямоугольный треугольник, равновеликий данному прямоугольнику.
9.16. Через данную точку А, лежащую вне окружности, провести прямую так, чтобы отношение AM : MN было равно отношению двух данных отрезков а и Ъ, М и JV — точки пересечения прямой с окружностью и М лежит между А и N.
9.17. Через вершину Л данного квадрата ABCD со стороной а провести прямую так, чтобы отрезок этой прямой, ограниченный точками ее пересечения с CD и продолжением ВС, был равен данному отрезку I.
9.18. Провести прямую, параллельную стороне АС треугольника АВС и пересекающую две другие стороны АВ и ВС соответственно в точках М и N, так, чтобы площадь треугольник MBN относилась к площади трапеции AMNC как т : п, где тип — данные отрезки.
9.19. Через данные точки А и В провести окружность, отсекающую от данной прямой МК хорду данной длины I.
9.20. Построить прямоугольный треугольник по его гипотенузе с и сумме S одного из его катетов и проведенной к нему медиане.
9.21. Построить прямоугольный треугольник по радиусу R описанной около него окружности и радиусу г вписанной в него окружности.
9.22. Построить правильный 15-угольник, вписанный в данную окружность.
9.23. Провести три различные прямые, параллельные основаниям трапеции и пересекающие боковые стороны так, чтобы данная трапеция разбилась этими прямыми на четыре равновеликие.