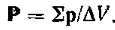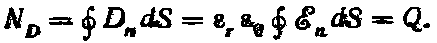В предыдущей статье было показано, что вследствие поляризации диэлектрика, т. е. смещения его связанных зарядов, изменяется напряженность электрического поля. Результирующее влияние диэлектрика на электрическое поле оценивают векторной величиной, называемой поляризованностью Р (вектором поляризации).
Средняя интенсивность поляризации Pср определяется как сумма дипольных моментов в единице объема диэлектрика, а чтобы найти поляризованность в данном месте поля, надо выбрать достаточно малый объем ΔV:
Единица измерения поляризованности
[P] = [ql/V] = Кл*м/м 3 = Кл/м 2.
Вектор поляризации направлен навстречу вектору напряженности электрического поля связанных зарядов Eп.(рис. 4.12).
Вектор поляризации для большинства диэлектриков (за исключением группы сегнетоэлектриков) пропорционален напряженности электрического поля:
и его направление совпадает с направлением внешнего Eвн и результирующего Е полей (риc. 4.12).
Коэффициент k называется электрической восприимчивостью диэлектрика и характеризует его способность поляризоваться.
При расчетах электрических полей в диэлектриках с различными диэлектрическими проницаемостями пользуются еще вектором электрического смещения.
Электрическое смещение D связано с напряженностью электрического ноля простым соотношением
откуда можно определить единицу намерения электрического смещения:
которая такая же, как у вектора, поляризации и у поверхностной плотности зарядов на электродах.
Электрическое смещение и поверхностная плотность свободных зарядов численно одинаковы на поверхности всех проводящих тел, находящихся в электростатическом поле. Например, у внутренней поверхности пластины плоского конденсатора (рис. 4.8) напряженность однородного электрического поля, как и в любой точке однородного поля (4.10),
а электрическое смещение в любой точке поля, в том числе и у металлической поверхности,
т. е. совпадает с поверхностной плотностью заряда на пластине.
Из (2а) следует, что при заданной плотности поверхностных свободных зарядов на электродах электрическое смещение в однородном диэлектрике с диэлектрической проницаемостью εa не зависит от εa, а напряженность электрического поля зависит. Поэтому можно сказать, что на напряженность электрического поля определяется и свободными (на электродах) и связанными (в диэлектриках) зарядами, т. е. поляризацией диэлектрика, а электрическое смещение в однородном диэлектрике не зависит от связанных зарядов.
Связь между тремя векторными величинами, характеризующими электрическое поле в диэлектрике, выражается равенством
Приняв во внимание (1) и (2), получим
откуда диэлектрическая проницаемость
а электрическая восприимчивость

Рассмотрим еще неоднородное электрическое поле заряженного металлическою шара (рис. 1), радиус которого Rш. Известно, что электрический заряд Q находится на поверхности такого шара. Поверхностная плотность заряда
Поле металлического шара с зарядом Q совпадает вне шара с полем равного ему по значению точечного заряда Q, расположенного в центре шара (4.8); поэтому напряженность поля на расстоянии R от центра шара и в частности, у его наружной поверхности, т.е. при R = Rш,
а электрическое смещение
т. е. равно поверхностной плотности заряда.
Внутри металлического шара поля нет, как и во всяком проводнике в условиях электростатики , Поэтому потенциалы всех точек шара одинаковые, т. е. шар — эквипотенциальное тело, как и всякое металлическое тело в электростатическом поле.
Аналогично потоку вектора напряженности поля (4.7) применяется понятие потока вектора электрического смешения.
Поток вектора смещения ND в однородном поле равен произведению численного значения вектора смещения D и площадки S, во всех точках которой вектор смещения имеет одинаковое значение и направлен перпендикулярно к ней, т. е.
При неоднородном поле произвольную поверхность площадью S разбивают на элементарные, в пределах каждой на которых смещение одинаково; так что поток вектора
смещения через такую элементарную площадку
где Dn— нормальная составляющая вектора смещения (перпендикулярная к элементарной площадке).
Поток вектора смещения через произвольную замкнутую поверхность находится суммированием элементарных потоков: 
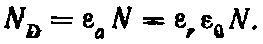
В частности, в случае шаровой поверхности
Таким образом, поток вектора электрического смещения через шаровую поверхность равен заряду, расположенному внутри поверхности.
Полученное выражение ND = Q справедливо для замкнутой поверхности любой формы, охватывающей заряд как в однородной среде с εr = const, так и в среде, диэлектрическая проницаемость которой неодинакова в различных участках среды, например в двухслойном конденсаторе.
На поверхности шара,
откуда определяется электрическое смещение у поверхности шара: что согласуется с (5).
Видео:Поляризация диэлектрикаСкачать

Поляризованность. Диэлектрическая восприимчивость. Диэлектрическая проницаемость
Количественной характеристикой поляризации диэлектрика служит вектор Р, называемый поляризованностью.
Поляризованность (вектор поляризации) определяется как дипольный момент единицы объема диэлектрика, равный отношению электрического дипольного момента малого объема диэлектрика к этому объему AV:
где Pi —qlj — электрический дипольный момент /-й молекулы; п — общее число молекул в объеме AV. Этот объем должен быть настолько мал, чтобы в его пределах электрическое поле можно было считать однородным.
Число молекул в А Vдолжно быть достаточно велико, чтобы к ним можно было применить статистические закономерности: п » 1.
Единица поляризованности в СИ — кулон на метр в квадрате (Кл/м 2 ).
В случае изотропных диэлектриков (за исключением сегнетоэлектри- ков и некоторых ионных кристаллов), чьи свойства не зависят от направления, поляризованность линейно зависит от напряженности результирующего (13.1) поля:
где х — безразмерная величина — диэлектрическая восприимчивость вещества, характеризующая свойства диэлектрика. Всегда х > О- Диэлектрическая восприимчивость не зависит от напряженности Е.
Отметим, что в сильных электрических полях зависимость поляризованности Р от напряженности Е поля в диэлектрике может быть нелинейной.
Можно доказать теорему Гаусса для поля вектора поляризации: поток вектора поляризации Р сквозь произвольную замкнутую поверхность S равен взятому с обратным знаком избыточному связанному заряду диэлектрика в объеме V, охватываемом поверхностью S, т.е.
где р’ — объемная плотность нескомпенсированного связанного заряда. В дифференциальной форме уравнение (13.4) имеет следующий вид:
т.е. дивергенция поля вектора Р равна взятой с обратным знаком объемной плотности избыточного связанного заряда в той же точке. Линии Р начинаются на отрицательных и заканчиваются на положительных связанных зарядах.
Величина плотности нескомпенсированного связанного заряда р’ в диэлектрике связана с плотностью сторонних зарядов формулой
Следовательно, объемные связанные заряды внутри диэлектрика будут отсутствовать при одновременном выполнении двух условий:
Рис. 13.2. Напряженность электрического поля Е внутри диэлектрика
- 1) диэлектрик является однородным (Vx = 0);
- 2) сторонние заряды внутри его отсутствуют (р = 0).
Поместим пластинку из однородного диэлектрика во внешнее электрическое поле, созданное двумя бесконечными параллельными разноименно заряженными плоскостями (рис. 13.2). В диэлектрике поле Е’ создается связанными зарядами и направлено против внешнего поля Е0, создаваемого сторонними зарядами. Результирующее поле внутри диэлектрика, согласно формуле (13.1), определяется как
С помощью теоремы Гаусса (12.11) можно вычислить напряженность между двумя разноименно заряженными плоскостями (см. выражение (12.42)):
где о — поверхностная плотность стороннего заряда на металлических обкладках конденсатора. По аналогии можно записать для поля Е
где о’ — поверхностная плотность связанных зарядов.
Тогда получаем, что напряженность поля внутри диэлектрика
совпадает с напряженностью поля в вакууме, когда поверхностная плотность заряда на обкладках конденсатора равна (о — о’).
Можно показать, что на границе диэлектрика и вакуума поверхностная плотность связанных зарядов о’ равна нормальной составляющей вектора поляризации в данной точке поверхности:
где Рп — проекция вектора Р на внешнюю нормаль к поверхности данного диэлектрика; Еп — проекция вектора Е (внутри диэлектрика вблизи его поверхности) на внешнюю нормаль. Следовательно, знак Рп определяет знак о’.
Тогда из формул (13.7) и (13.7а) можно записать:
Напряженность результирующего поля внутри диэлектрика
тг — диэлектрическая проницаемость среды. Она характери- Е
зует способность диэлектрика поляризоваться в электрическом поле и показывает, во сколько раз поле ослабляется диэлектриком (см. подтему 12.1). Отметим, что для всех веществ е>1. Для вакуума е = 1, для газов ? мало отличается от 1, для воды ? = 81, а для некоторых керамик может достигать многих тысяч. Для электроизолирующих материалов, например для мягкой резины, ? = 2,6—3, для ультрафарфора (керамика) ? = 6,3—7,5, для стекла ? = 4—10.
При наличии диэлектрика теорема Гаусса для вектора Е (12.11) и эквивалентное уравнение (12.13) обычно записываются так:
Видео:44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать

Вектор поляризации
Вы будете перенаправлены на Автор24
Видео:Билет №06-08 "Диэлектрики"Скачать

Что такое вектор поляризации
Для того, чтобы с количественной точки зрения описать поляризацию диэлектрика, пользуются вектором поляризации (поляризованностью ($overrightarrow
$)), который является электрическим моментом единицы объема диэлектрика:
где $overrightarrow$ — дипольный момент элемента диэлектрика.
В том случае, если диэлектрик состоит из неполярных молекул, то дипольный момент диэлектрика можно разделить на две части: момент каждой молекулы и дипольные моменты всех молекул в единице объема.
Получается, что для неполярных молекул вектор поляризованности можно определить, как:
где суммирование идет относительно всех молекул в объеме $triangle V$. $N$ — концентрация молекул, $overrightarrow
$ — индуцированный дипольный момент (Он одинаковый у всех молекул). $overrightarrow
uparrow uparrow overrightarrow$.
Видео:Лекция 4 -1 Поляризация диэлектриковСкачать

Формула поляризованности для полярных молекул
Формула поляризованности для полярных молекул имеет вид:
где $leftlangle overrightarrow
rightrangle $ — среднее значение дипольных моментов, которые равны по модулю, но разнонаправлены.
В изотропных диэлектриках средние дипольные моменты совпадают по направлению с напряженностью внешнего электрического поля. У диэлектриков с полярного типа молекулами, вклад в поляризованность от наведенных зарядов много меньше, чем вклад от переориентации поля.
Ионная решеточная поляризации описывается формулой (3). В большинстве случаев такая поляризация является анизотропной.
У электретов (диэлектрические вещества, которые в отсутствии электрического поля долгое время сохраняют поляризованность) и сегнетоэлектриков (диэлектрические вещества, которые при определенных температурах могут спонтанно поляризоваться при отсутствии внешнего электрического поля) поляризованность может быть отлична от нуля даже если $overrightarrow=0.$ У остальных диэлектриков при $overrightarrow=0$, $overrightarrow
=0$. У изотропных диэлектриков поляризованность связана с напряженностью поля в той же точке уравнением (система СИ):
[overrightarrow
=varkappa _0overrightarrow left(4right),]
где $varkappa $ — диэлектрическая восприимчивость (безразмерная величина).
В анизотропных диэлектриках направление вектора напряженности и вектора поляризации не совпадают. И их связь устанавливается в виде:
где индексы i,j — нумеруют компоненты по осям декартовой системы координат ($i=x, y,z;j=x, y,z. )$), $_$ — тензор диэлектрической восприимчивости.
Зависимость $overrightarrow
(overrightarrow)$ в общем случае представлена в виде:
Формула (6) показывает, что поляризованность зависит не только от первой степени напряженности электрического поля, но и от ее высших степеней. Если зависимость в (6) от высших степеней играет существенную роль, то диэлектрик нелинейный. Подобная нелинейность проявляется в сильных полях, так же существуют некоторые специальные вещества. Если нелинейность не существенна, то используют формулы вида (5).
При неоднородной поляризации, поляризационные заряды могут появляться не только на поверхности диэлектрика, но и в его объеме. Плотность объемных связанных зарядов ($_$) равна:
Формула (7) показывает, что объемные заряды возникают только в случае неоднородной поляризации. При переходе из одного диэлектрика в другой, поверхностная плотность связанных зарядов ($_$) равна:
где $overrightarrow$- единичный вектор нормали, который направлен из первой во вторую среду, $overrightarrow
;;overrightarrow
$ — векторы поляризации второй и первой среды. Заметим, что вакуум можно рассматривать как диэлектрик, поляризованность которого равна нулю.
Единица измерения $left[Pright]=frac$.
Готовые работы на аналогичную тему
Задание: Чему равна объемная плотность зарядов в диэлектрике, если вектор поляризованности задан функцией: $overrightarrow
=frac<overrightarrow>,$ где $overrightarrow$ — единичный орт, r — модуль радиус-вектора.
Основой для решения задачи служит формула связи плотности объёмных зарядов с вектором поляризации диэлектрика:
В нашем случае, формула (1.1) преобразуется к виду:
Ответ: Объемная плотность зарядов при заданном векторе поляризованности равна нулю.
Задание: Вектор поляризации бесконечной пластины поляризованного диэлектрика задан выражением: $overrightarrow
Вектор напряженности и вектор поляризации направлены в разные стороны.
Основанием для решения задачи выберем уравнение:
Следовательно, если мы знаем закон изменения вектора поляризации из условия задачи, следовательно:
Разность потенциалов может быть найдена, если известен закон изменения напряженности, как:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 04 12 2022
💡 Видео
Лекция №4 "Диэлектрики, вектор электрической индукции"Скачать

Диэлектрики в электростатическом поле. Поляризация диэлектриков | Физика 10 класс #48 | ИнфоурокСкачать

Лекция 4-5 Доказательство теоремы Гаусса для вектора поляризацииСкачать

Поляризация света и закон МалюсаСкачать

Кокшаров Ю. А. - Электромагнетизм - Диэлектрики в электростатическом полеСкачать

Лекция 237. Вектор электрической индукцииСкачать

ЧК_МИФ 3_1_5_1 _(L3) ВЕКТОР ЭЛЕКТРИЧЕСКОЙ ПОЛЯРИЗАЦИИСкачать

Диэлектрики в электрическом поле. 10 класс.Скачать

Поляризация света. ФизикаСкачать

Поляризация диэлектриковСкачать

Урок 228. Диэлектрики в электрическом поле. Диэлектрическая проницаемостьСкачать

Диэлектрики в электрическом полеСкачать

Поляризация светаСкачать

ЧК_МИФ 3_1_5_1 _(L4) ВЕКТОР ЭЛЕКТРИЧЕСКОЙ ПОЛЯРИЗАЦИИСкачать

Лекция №3 "Электростатика. Поляризация диэлектриков"Скачать

ЭП в веществе 2 Виды поляризацииСкачать