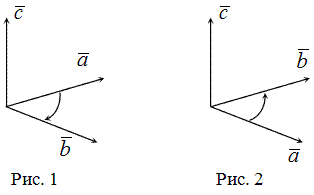
Как узнать ориентацию тройки векторов (6 видео)

Как узнать ориентацию тройки векторов

Для дальнейшего изучения свойств пространства необходимо ввести определение ориентации пространства. Строгая теория, касающаяся этого понятия не очень сложна, но достаточно суха. В связи с этим ограничимся лишь некоторыми “качественными” пояснениями.

Итак, все упорядоченные некомпланарные тройки векторов могут быть разбиты на два непересекающихся класса: правые тройки и левые тройки.

Определение 1: Упорядоченная тройка некомпланарных векторов а 1 , а 2 , а 3 называется правой, если наблюдателю, находящемуся внутри телесного угла, образованного этими векторами, кратчайшие повороты от а 1 к а 2 и от а 2 к а 3 кажутся происходящими против часовой стрелки. Если повороты происходят по часовой стрелке, то тройка – левая.

Есть и ещё один способ разделить эти два класса:

Правило правой руки: Совместите начала всех векторов тройки в одной точке. Представьте, что в этой точке находится ладонь Вашей правой руки. Совместите большой палец с первым вектором базиса, а указательный – со вторым. Если теперь вы сможете совместить средний палец с третьим вектором, то рассматриваемая тройка векторов – правая. Если нет – левая.

Выбрав один из двух классов и назвав все входящие в него базисы “положительными” мы зададим ориентацию пространства.

Далее будем считать положительными правые тройки векторов. Все дальнейшие определения будем давать с учетом этого

Определение 2: Скалярное произведение ставит в соответствие паре векторов a и b число ( a , b )=| a | · | b | · cosφ a , b .

Свойства скалярного произведения:

1. коммутативность: ( a , b )=( b , a )

3. ( a , b )=0 a b

4. Дистрибутивность: ( a 1 + а 2 , b )= ( a 1 , b )+ ( a 2 , b )

5. ( а , λ ·b )= λ · ( a , b ) λ R .

Утверждение 1: В декартовом базисе если а =, b =, то ( a , b )= x 1 · x 2 + y 1 · y 2 + z 1 · z 2 .

Пример 1. Найти угол между векторами.

Определение 3: Векторным произведением упорядоченной пары векторов a и b называется вектор [ a , b ], такой что

| [ a , b ] |=S a , b , где S a , b – площадь параллелограмма, построенного на векторах a и b . (Если a || b , то S a , b =0.)
a[ a , b ] b .
a, b , [ a , b ] – правая тройка.

Свойства векторного произведения:

[ a , b ] = -[ b , a ]
[ a , b ] = θ ó a || b
[ a 1 + a 2 , b ] = [ a 1 , b ]+[ a 2 , b ]
λ·[ a , b ] = [λ ·a , b ] = [ a ,λ ·b ] λ R .

Утверждение 2: В декартовой системе координат (базис i , j , k ), a =, b =

=> [ a , b ] =

Пример 2. Вычислить площадь параллелограмма, построенного на векторах a и b.

Определение 4: Смешанным произведением упорядоченной тройки векторов a , b и c называется число , b , c> , т.ч. a , b , c >=([ a , b ], c ).

Утверждение 3: a , b , c >=V a , b , c , если a , b , c – правая тройка, или a , b , c >= -V a , b , c , если a , b , c – левая тройка. Здесь V a , b , c – объём параллелепипеда, построенного на векторах a , b и c . (Если a , b и c компланарны, то V a , b , c =0.)

Утверждение 4: В декартовой системе координат, если a =, b =,

с =, => a , b , c >=.

Пример 3. Проверка компланарности векторов.

Пример 4. Принадлежность 4 точек одной плоскости.

Пример 5. Вычислить объем тетраэдра и его высоту.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Содержание

Ориентация векторов на плоскости
Ориентация плоскости и пространства
Векторы на плоскости и в пространстве — основные определения
Определение вектора
Нулевой вектор
Длина вектора
Коллинеарность векторов
Направление векторов
Равные и противоположные векторы
Углы между векторами
Правая и левая тройки векторов
Остались вопросы?
Все еще сложно?
💥 Видео

Видео:§11 Ориентация векторов в пространствеСкачать

Ориентация векторов на плоскости

Видео:Ориентация векторов в пространстве. Правая и левая тройки векторовСкачать

Ориентация плоскости и пространства

Базис (е_х,е₂) векторного пространства V₂ плоскости Е₂ называется правым, если кратчайший поровот от первого вектора е_х к вектору е₂ происходит против часовой стрелки.

Базис (е_1? е₂) векторного пространства И₂ плоскости Е₂ называется левым, если кратчайший поровот от первого вектора е _{0, а если по часовой – то a 0 . Таким образом, – p a £ p . Если a > 0, то пара векторов (, ) называется правой, а если a 0 – то левой.}

В пространстве понятие ориентированного угла не имеет смысла. Если посмотреть на плоскость, в которой лежат лучи OA и OB с одной стороны, то увидим, что кратчайший поворот от OA к OB осуществляется в одном направлении, а если посмотреть на плоскость с другой стороны, то мы увидим тот же поворот в другом направлении.

Пусть в пространстве даны три некомпланарных вектора , , . Отложим их из одной точки О: = , = , = . Тройка векторов (, , ) называется правой, если кратчайший поворот от луча OA к лучу OB, если смотреть из точки C , выглядит как осуществляющийся против часовой стрелки. Соответственно, если этот поворот выглядит как осуществляющийся по часовой стрелке, то тройка векторов (, , ) называется левой. На рисунке изображена правая тройка векторов.

Проекция вектора на ось.

Пусть l – некоторая прямая в пространстве. Выберем точку OÎ l и единичный вектор ||l.Построим направленный отрезок = . Прямая l с отрезком называется осью. Иногда говорят, что ось – это прямая, на которой задано направление.

Определение. Пусть – произвольный вектор, а – произвольный направленный отрезок, который представляет . Опустим перпендикуляры AA₁ и BB₁ на прямую l. Пусть = . Тогда вектор

называется векторной проекцией вектора на ось l и обозначается p_l.

Мы имеем || . Поэтому согласно теореме 1 существует такое число p, что = p. Это число называется скалярной проекцией вектора на ось l . Поскольку –

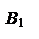
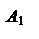
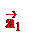
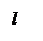
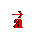
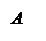
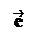
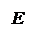
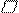
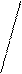
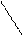
единичный вектор, то p – это длина вектора , если , и p = – ||, если ¯. Будем обозначать скалярную проекцию так: P_l.

Зная скалярную проекцию вектора мы можем найти его векторную проекцию:

Необходимо еще доказать, что определения скалярной и векторной проекции корректны, т.е. не зависят от выбора направленного отрезка , который представляет вектор . Другими словами, если мы отложим вектор от другой точки, то его скалярная и векторная проекции не изменятся,– и это надо доказать.

Проведем через точки A и B плоскости a и b перпендикулярно l. Тогда ½p½=½P_l½ есть расстояние между a и b .Выберем другой направленный отрезок , представляющий и проведем через точки A¢, B ¢ плоскости a¢ и b¢ перпендикулярно l. Направленные отрезки и эквивалентны, а значит, они совмещаются параллельным переносом. При этом переносе плоскость a совместится с a¢, а плоскость b – с b¢. Значит, расстояние между a¢ и b¢ равно расстоянию между a и b, и оно равно ½p½. Поэтому ½p½ не зависит от выбора направленного отрезка. Направление векторной проекции также не изменится при переносе, поэтому и знак p не изменится. Итак, скалярная проекция не зависит от выбора направленного отрезка, представляющего . В силу равенства (*) p_l также не зависит от выбора направленного отрезка.

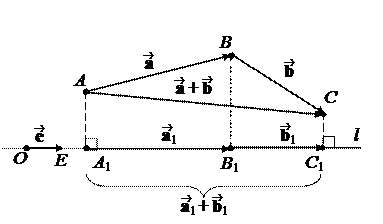
Теорема 2. Свойства проекции вектора на ось.

1.P_l =| | cosÐ(, );

Доказательство. 1. Поскольку определение проекции не зависит от выбора точки A ,из которой отложен вектор , мы можем отложить его из точки О. Обозначим j =Ð(, ).

1 случай: j £ p/2. Тогда из DOBB₁ получим, что

2 случай: j > p/2. Тогда из DOBB₁ получим, что

2. Для скалярных проекций:

1 случай: l > 0. Тогда l и Ð(, l ) = j. Значит,

= l| |cos j = lP_l .

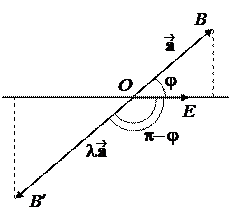
Ð(, l ) = p – j и cosÐ(,l ) = – cos j,

3случай: l = 0. Тогда равенство очевидно.

Для векторных проекций с помощью равенства (*) получаем:

3.Доказательство для векторных проекций показано на чертеже, но только для случая векторов на плоскости. Рисунок для векторов в пространстве можно найти в учебнике [10].

Для скалярных проекций равенство вытекает из равенства для векторных проекций. Например, в случае, изображенном на втором рисунке,

|A₁C₁|= |A₁B₁|+(– |B₁C₁|).

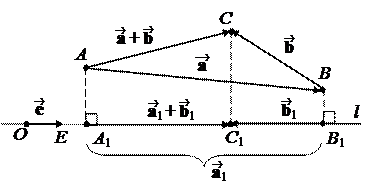
Видео:Правые и левые тройки векторовСкачать

Векторы на плоскости и в пространстве — основные определения

Видео:Смешанное произведение векторовСкачать

Определение вектора

В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.

Для начала дадим определение:

Вектор – это направленный отрезок прямой.

Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.

В математике для обозначения вектора обычно используют строчные латинские буквы, однако над вектором всегда ставится небольшая стрелочка, например a → . Если известны граничные точки вектора – его начало и конец, к примеру A и B , то вектор обозначается так A B → .

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Нулевой вектор

Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.

Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.

Видео:Аналитическая геометрия, 3 урок, Векторное произведениеСкачать

Длина вектора

Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.

Длину вектора A B → принято обозначать так A B → .

Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.

Видео:18+ Математика без Ху!ни. Векторное произведение.Скачать

Коллинеарность векторов

Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.

Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.

Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.

Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.

Видео:Векторное произведение векторовСкачать

Направление векторов

Сонаправленными векторами называют два коллинеарных вектора a → и b → , у которых направления совпадают, такие векторы обозначаются так a → ↑ ↑ b → .

Противоположно направленными векторами называются два коллинеарных вектора a → и b → , у которых направления не совпадают, т.е. являются противоположными, такие векторы обозначаются следующим образом a → ↑ ↓ b → .

Считается, что нулевой вектор является сонаправленым к любым другим векторам.

Видео:Коллинеарность векторовСкачать

Равные и противоположные векторы

Равными называются сонаправленные вектора, у которых длины равны.

Противопожными называются противоположно направленные вектора, у которых их длины равны.

Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.

Пусть заданы два произвольных вектора на плоскости или в пространстве a → и b → . Отложим от некоторой точки O плоскости или пространства векторы O A → = a → и O B → = b → . Лучи OA и OB образуют угол ∠ A O B = φ .

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Углы между векторами

Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .

Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.

Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).

Видео:Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать