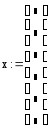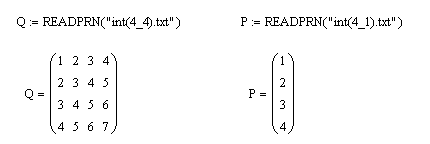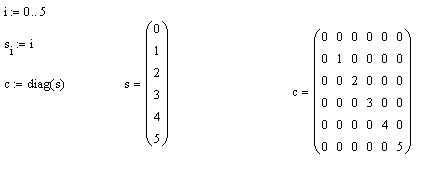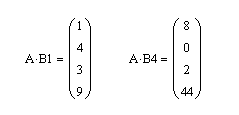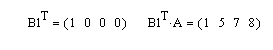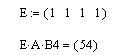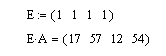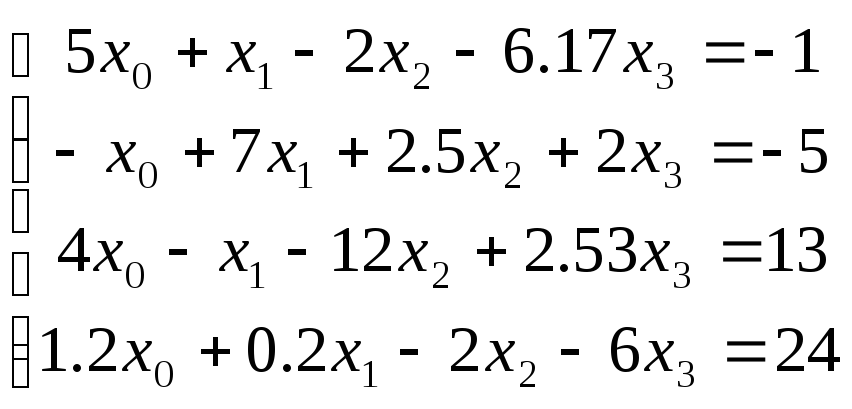Как создать вектор из строки матрицы (7 видео)

Как создать вектор из строки матрицы

Одиночное число в Mathcad называется скаляром. Столбец чисел называется вектором, а прямоугольная таблица чисел — матрицей. Общий термин для вектора или матрицы — массив.

Имеются три способа создать массив:

Заполняя массив пустых полей, как обсуждается в этом разделе. Эта методика подходит для не слишком больших массивов.
Используя дискретный аргумент, чтобы определить элементы с его помощью, как обсуждено в следующей главе. Эта методика подходит, когда имеется некоторая явная формула для вычисления элементов через их индексы.
Считывая их из файлов данных.

Можно различать имена матриц, векторов и скаляров, используя различный шрифт для их написания. Например, во многих математических и инженерных книгах имена векторов пишутся жирным, а имена скалярных переменных — курсивом.

Вектор — массив или матрица, содержащая один столбец. Чтобы создать вектор в Mathcad, выполните следующее:

Щёлкните в свободном месте или на поле.

Выберите Матрицы из меню Математика или нажмите [Ctrl]M. Появляетс я диалоговое окно, как на рисунке справа.

Укажите число строк, равное числу элементов вектора, в поле “Строк”. Например, чтобы создать вектор с тремя элементами, напечатайте 3.
Напечатайте 1 в поле “Столбцов”, затем нажмите “Создать”. Mathcad создает вектор с пустыми полями для заполнения.

На следующем этапе нужно заполнить эти поля скалярными выражениями. Для этого выполните следующее:

Щёлкните на верхнем поле и напечатайте 2.

Переместите выделяющую рамку в следующее поле. Можно сделать это или клавишей [Tab], или щёлкнув непосредственно на втором поле.

Напечатайте 3 во втором поле. Затем переместите выделяющую рамку в третье поле, и напечатайте 4.

Если понадобится создавать еще векторы, можно оставить диалоговое окно “Матрицы” открытым для дальнейшего использования.

Как только вектор создан, можно использовать его в вычислениях в точности так же, как и число. Например, чтобы добавить другой вектор к этому вектору, необходимо выполнить следующее:

Нажмите [ ] несколько раз или щёлкните на любой из скобок вектора. Выделяющая рамка теперь заключает весь вектор. Это означает, что знак плюс, который будет напечатан, относится к вектору целиком, а не к какому-либо из элементов.

Нажмите клавишу плюс (+). Mathcad показывает поле для второго вектора.

Используйте диалоговое окно “Матрицы”, чтобы создать другой вектор с тремя элементами.

Заполните этот вектор, щелкая в каждом поле и печатая числа, показанные справа. Можно также использовать [Tab], чтобы двигаться от одного элемента к другому.

Нажмите знак =, чтобы увидеть результат.

Сложение — только одна из операций Mathcad, определенных для векторов и матриц. В Mathcad также есть вычитание матриц, умножение матриц, скалярное произведение, целочисленные степени, детерминанты и много других операторов и функций для векторов и матриц. Полные списки появляются в разделах “Векторные и матричные операторы” и “Векторные и матричные функции” ниже в этой главе.

Если Вы используете Mathcad PLUS, Вы сможете выполнить много символьных операций с матрицами. Подробнее об этом см.в Главе “Символьные вычисления”.

Чтобы создать матрицу, сначала щёлкните в свободном месте или на поле. Затем:

Выберите Матрицы из меню Математика, или нажмите [Ctrl]M. Появится диалоговое окно.

Введите число строк и столбцов в нужные поля. В этом примере матрица имеет две строки и три столбца. Затем нажмите на “Создать”. Mathcad создаст матрицу с пустыми полями.

В завершение заполните поля, как описано в предыдущем разделе для векторов.

Можно использовать эту матрицу в формулах в точности так же, как и число или вектор.

Везде в настоящем руководстве термин вектор относится к вектору-столбцу. Вектор-столбец идентичен матрице с одним столбцом. Можно также создать вектор-строку, создав матрицу с одной строкой и многими столбцами. Операторы и функции, которые берут векторный аргумент, всегда ожидают вектор-столбец. Они не применимы к векторам-строкам. Чтобы превратить вектор-строку в вектор-столбец, используйте оператор транспонирования[Ctrl]1.

Изменение размера матрицы

Можно изменять размер матрицы, вставляя и удаляя строки и столбцы. Для этого необходимо выполнить следующее:

Щёлкните на одном из элементов матрицы, чтобы заключить его в выделяющую рамку. Mathcad будет начинать вставку или удаление с этого элемента.

Выберите Матрицы из меню Математика. Появляется диалоговое окно.

Напечатайте число строк и-или столбцов, которые нужно вставить или удалить. Затем нажмите на “Вставить” или на “Удалить”. Например, чтобы удалить столбец, который содержит выбранный элемент, напечайте 1 в поле “Столбцов”, 0 в поле “Строк”, и нажмите на “Удалить”.

Вот как Mathcad будет удалять или вставлять строки или столбцы, в зависимости от того, что впечатывается в диалоговое окно:

Если вставляются строки, Mathcad создает строки пустых полей ниже выбранного элемента. Если вставляются столбцы, Mathcad создает столбцы пустых полей справа от выбранного элемента.
Чтобы вставить строку выше верхней строки или столбец слева от первого столбца, сначала заключите матрицу целиком в выделяющую рамку, щёлкнув внутри и нажав [ ] несколько раз. Затем выберите Матрицы и продолжите, как обычно.
Когда строки или столбцы удаляются, Mathcad начинает со строки или столбца, занятых выбранным элементом. Mathcad удаляет строки вниз от этого элемента и столбцы — направо от этого элемента.
Если напечатать 0 в поле “Строк”, Mathcad ни вставит, ни удалит строки. Если напечатать 0 в поле “Столбцов”, Mathcad ни вставит, ни удалит столбцы.

Обратите внимание, что при удалении строк или столбцов Mathcad выбрасывает содержащуюся в них информацию.

Чтобы удалить всю матрицу или вектор, заключите их в выделяющую рамку и выберите Вырезать из меню Правка.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Содержание

Лекція№9 — Операции с векторами и матрицами, матричные функции в математическом пакете MathCad
3.1. Создание векторов и матриц
3.2. Использование матриц специального вида для выполнения матричных операций в системе MathCad
3.3. Решение систем линейных алгебраических уравнений с использованием матричных преобразований
Двумерный вектор в C++
Пример 1. Создайте двумерный вектор из равного количества столбцов
Пример 2: Создайте двумерный вектор с другим количеством столбцов
Пример 3: Инициализировать двумерный пустой вектор со значением по умолчанию
Пример 4: Инициализировать двумерный пустой вектор, принимая входные значения
Заключение
📽️ Видео

Видео:Работа с массивами. Вектор столбцы и вектор строки 1. Урок 7Скачать

Лекція№9 — Операции с векторами и матрицами, матричные функции в математическом пакете MathCad

Матричное исчисление играет важную роль в компьютерной математике. Практически все численные методы на том или ином этапе работы своего алгоритма сводятся к решению систем линейных алгебраических уравнений (СЛАУ), которое часто производится матричными методами. Вообще говоря, нельзя назвать ни одной области использования компьютера, в алгоритмах которой (в большей или меньшей степени) не использовались бы матрицы.

Понятие «вектор» обычно не отделяют от понятия «матриц». Векторы могут рассматриваться как матрицы, состоящие из одного столбца (или строки).

Матричные вычисления в MathCAD можно условно разделить на три основных типа.

К первому относятся такие элементарные действия над матрицами, как создание, извлечение из них данных, их умножение, сложение или скалярное произведение (в случае векторов). Для их реализации служат специальные операторы трех панелей семейства Math (Математические): Calculator (Калькулятор), Matrix (Матричные) иSymbolics (Символьные).

Ко второму типу можно отнести те матричные преобразования, которые требуют использования специальных функций и встроенных алгоритмов матричной алгебры, таких как, например, функции вычисления определителя, матричных норм или сортировки элементов векторов по возрастанию. Функции этой группы можно найти в категории Vector and Matrix (Векторные и матричные) у мастера функций.

И, наконец, к третьему типу матричных вычислений следует отнести те задачи, решить которые можно только используя возможности системы программирования MathCAD.

В языках программирования начальные индексы массивов обычно равняются 0. По умолчанию в MathCAD индексы строк и столбцов также отсчитываются с 0. В том случае, если такая система вам неудобна или непривычна, можно изменить точку отсчета индексов на 1, задав системную переменную ORIGIN: ORIGIN:= 1.

Доступ к элементам вектора или матрицы осуществляется с помощью индексированных переменных. Например, чтобы использовать пятый элемент вектора с именем А, нужно записать этот элемент в виде: . А для того, чтобы взять элемент матрицы В, расположенный на пересечении 3-ей строчки и 4-го столбца нужно записать: .

Для задания индексов на панели Matrix предусмотрена специальная кнопка Subscript (Индекс). Перейти к записи индекса можно также с помощью клавиши «[» ( левая квадратная скобка). Нажав ее, вы увидите, что на месте будущего индекса, чуть ниже текста имени матрицы, появится черный маркер. В него через запятую следует ввести значения индексов. На первом месте при этом должен стоять номер строки, а на втором – столбца.

Видео:Матрицы и векторыСкачать

3.1. Создание векторов и матриц

В системе предусмотрены различные возможности задания векторов и матриц:

Определение матрицы последовательным заданием каждого элемента.

С помощью индексированных переменных.

С помощью использования команды Insert→Matrix, либо с помощью соответствующей кнопки панели Matrix.

Задание с помощью элементов программирования.

Применение встроенных функций.

Через связь с другим приложением, например Excel.

Создание таблицы данных.

Чтение из внешнего файла.

Рассмотрим некоторые из них. Определение матрицы последовательным заданием каждого элемента очевидно и не требует пояснений. При создании матрицы или вектора с помощью индексированной переменной следует исходить из того, что любая индексированная переменная, индексами которой являются переменные, принимающие целочисленные значения из некоторого промежутка, уже представляют собой вектор или матрицу.

Пример 1. Требуется сформировать вектор x, состоящий из 6 элементов. Элементам этого вектора присвоить значения индексов.

Решение. Предоставим два варианта решения этой задачи:

с помощью индексированной переменной;

с помощью команды Insert→Matrix.

Вариант а

Для того, чтобы сформировать вектор, воспользуемся вспомогательной переменной, которая будет играть роль индекса (например, i), а затем будем использовать эту переменную для здания элементных значений вектора x. Формирование вектора представлено на рис. 3.1.

Рис. 3.1. Формирование вектора с использованием индексированной переменной

Вариант b

Формирование вектора х будем производить с помощью команды Matrix. Для этого сначала напишем оператор присваивания: «х:=» , а затем выполним команду Matrix. Эта команда открывает диалоговое окно«Insert Matrix», которое представлено на рис. 3.2, в котором необходимо указать число строк и число столбцов. В нашем примере число строк равно 6, а число столбцов равно 1.

После нажатия кнопки «Ok» команда предоставит шаблон с шестью ячейками, в которые следует вписать значения элементов вектора.

Рис. 3.2. Вызов диалогового окна «Insert Matrix» для создания матрицы с помощью команды «Matrix»

Пример 2. В файле с именем «int(4_4).txt» записаны числа в виде матрицы четыре строчки по четыре элемента, разделенными пробелами. В файле с именем «int(4_1).txt» записаны числа в столбик. Требуется прочитать эти данные в матрицу Q и вектор P.

Решение. Для чтения данных из файла в матрицу/вектор можно воспользоваться функцией READPRN, которая имеет один параметр — имя файла. Фрагмент с решением представлен на рис. 3.3.

Рис. 3.3. Чтение данных из файлов

С матрицами могут производиться как численные, так и символьные вычисления. Операции с матрицами в системе MathCAD обозначаются так, как это принято в математике: —, +, *, … .

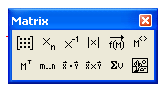
На рис. 3.4 показано назначение некоторых специализированных команд, расположенных на панели инструментов Matrix.

Помимо этого, система MathCAD представляет большое количество функций для работы с векторами и матрицами. Воспользоваться этими функциями можно с помощью мастера функций f(x).

Х -1 – получить обратную матрицу

|X| – вычислить детерминант

М Т – транспонировать

М – из матрицы взять вектор-столбец

v – получить сумму элементов

–скалярное произведение векторов

–векторное произведение векторов

Рис. 3.4. Назначение некоторых команд, расположенных на панели инструментов «Matrix»

На рис. 3.5 представлены вычисления с использованием операций над матрицами.

Рис. 3.5. Примеры матричных вычислений в MathCAD

Пример 3. Требуется сформировать диагональную квадратную матрицу с(6×6). Значения элементов главной диагонали должны совпадать с номером строки/столбца.

Решение. Для получения диагональной матрицы в системе предусмотрена функция diag, которая имеет один параметр – вектор диагональных элементов. Поэтому формирование матрицы начнем с создания вспомогательного вектора, в который занесем элементы для диагонали. Для формирования этого вспомогательного вектора (например, с именем s), воспользуемся вспомогательной переменной, которая будет играть роль индекса (например, i). Тогда формирование диагональной матрицы может быть получено в результате операций, как это показано на рис. 3.6.

Рис. 3.6. Формирование диагональной матрицы

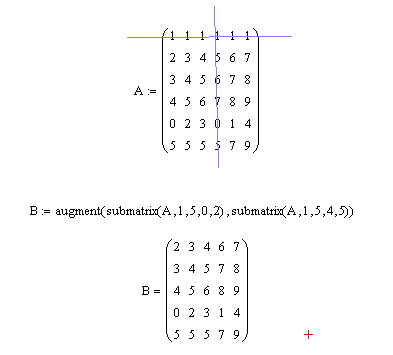
Пример 4. Даны две матрицы: А(4×3) и В(4×2). Требуется объединить эти матрицы в одну матрицу С(4×5), причем, первыми столбцами новой матрицы должны быть столбцы матрицы А, а справа от этих элементов следовать столбцы матрицы В (методом «дописывания справа»).

Решение. Для соединения двух матриц в одну матрицу можно использовать функцию augment, параметрами которой будут являться имена соединяемых матриц, как это показано на рис. 7.7.

Рис. 3.7. Объединения двух матриц по правилу «дописывания справа»

Пример 5. Даны две матрицы: А(2×3) и В(3×3). Требуется объединить эти матрицы в одну матрицу С(5×3), причем, в новой матрицы в качестве первых строк должны быть строки матрицы А, а за ними должны следовать строки матрицы В.

Решение. Для соединения двух матриц в одну матрицу по правилу «друг под другом» можно использовать функцию stack, параметрами которой будут являться имена соединяемых матриц, как это показано на рис. 3.8.

Рис. 3.8. Объединения двух матриц по правилу «друг под другом»

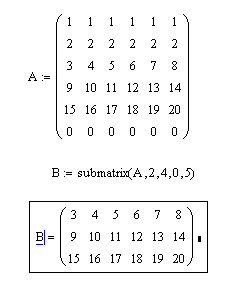
Пример 6. Дана матрица А(6×6). Требуется получить из этой матрицу подматрицу, в которую включить элементы, расположенные в строках, начиная с номера 2-го по номер 4-ый, и столбцах, начиная с номера 0-го по номер 5-ый.

Решение. Для выделения подматрицы с номерами столбцов и строк представленными граничными значениями предусмотрена функция submatrix. Эта функция имеет 5 параметров: имя матрицы, из которой производится выбор; начальный номер строки выбора; конечный номер строки выбора; начальный номер столбца выбора; конечный номер столбца выбора. Возможное решение представлено на рис. 3.9.

Рис. 3.9. Выделение подматрицы из заданной матрицы

Пример 7. Дана матрица А(6×6). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с 4–ым столбцом матрицы А, а второй – с 3-ей строкой матрицы А.

Решение. Для получения векторных значений можно воспользоваться командой М (из матрицы взять вектор-столбец), которая расположена на панели «Мatrix». Для получения первого вектора эту команду нужно применить непосредственно к матрице А, а для получения второго вектора нужно сначала получить из матрицы Атранспонированную матрицу, а только потом воспользоваться командой «взять столбец». Возможное решение представлено на рис. 3.10.

Рис. 3.10. Выделение векторных значений из заданной матрицы

Пример 8. Из матрицы А(6×6) выделить минор, который образуется в результате вычеркивания из этой матрицы нулевой строчки и третьего столбца.

Решение. Решение задачи можно свести к соединению двух подматриц, выделенных из матрицы А, как это показано на рис. 3.11.

Рис. 3.11. Выделение минора из заданной матрицы

Видео:MATLAB 04 Массивы и матрицыСкачать

3.2. Использование матриц специального вида для выполнения матричных операций в системе MathCad

Известно, что в результате умножении матрицы на вектор получается вектор. Причем, каждый i–ый элемент этого вектора-результата представляет собой сумму попарных произведений соответствующих элементов i–ой строки матрицы на элементы вектора-сомножителя. Очевидно, если в векторе, на который умножается матрица, все элементы равны нулю, а один элемент равен единице, то результатом такого произведения будет число, соответствующее тому элементуi–ой строки матрицы, где векторным сомножителем будет единица. Такой вывод можно использовать для выделения (формирования) из матрицы нужного столбца.

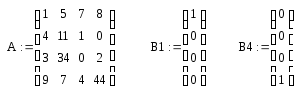
Пример 9. Даны матрица: А(4×4). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с 0–ым столбцом матрицы А, а второй — с 3-им столбцом матрицы А.

Решение. Для получения новых векторов сформируем два вспомогательных вектора: вектор B1 – с единичным значением в строке с номером 0, а второй вектор В4 – с единичным значением в строке с номером 3. Тогда для получения векторов в соответствии с условием задачи достаточно умножить матрицу А справа на векторы В1 и В2, как это показано на рис. 3.12.

Рис. 3.12. Выделение векторных значений из заданной матрицы

Аналогичным образом можно получить вектор-строку из матрицы. Для этого достаточно сформировать вспомогательный вектор — строку, у которой все компоненты равны нулю, а одна компонента, номер которой соответствует номеру выделяемой строки из матрицы, равна единице. Если этот вектор умножить слева на матрицу, то в результате будет получена нужная строка.

Пример 10. Дана матрица: А(4×4). Требуется выделить из матрицы первую строку по порядку (с номером 0).

Решение. Сначала требуется подготовить вспомогательный вектор-строку, а потом умножить эту строку слева на матрицу А. Вектор-строку можно получить из предыдущего примера транспонированием вектора-столбца В1.

Такой прием можно использовать для перестановки строк и столбцов матрицы, только для этого потребуется уже вспомогательная матрица, состоящая из векторов-столбцов (векторов-строк), место единичных элементы которых соответствуют тому порядку, который нужно иметь в результате преобразования матрицы.

Пример 11. Дана матрица: А(4×4). Требуется переставить в матрице строки с номерами 0 и 1.

Решение. Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в строках должно соответствовать нужному порядку для расположения строк в новой матрице. После этого решение можно получить простым перемножением матриц:

Пример 12. Дана матрица: А(4×4). Требуется переставить в матрице столбцы с номерами 0 и 1.

Решение. Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в столбцах соответствуют нужному порядку для выбора их в новую матрицу. После этого решение можно получить простым перемножением матриц:

Рассуждая, таким образом, можно с помощью вспомогательного вектора с единичными компонентами получить вектор, компоненты которого будут равны сумме строк (столбцов) матрицы, а также суммы отдельно выделенного столбика (строчки).

Пример 13. Дана матрица: А(4×4). Требуется найти сумму элементов в столбце с номером 3.

Решение. Для решения задачи требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение:

Пример 14. Дана матрица: А(4×4). Требуется получить вектора, элементы которого будут представлять суммы элементов в столбцах матрицы.

Решение. Для решения требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение:

Видео:#3. Функции автозаполнения, создания матриц и числовых диапазонов | NumPy урокиСкачать

3.3. Решение систем линейных алгебраических уравнений с использованием матричных преобразований

Для простоты решения ограничимся случаем системы из трех линейных уравнений с тремя неизвестными. Рассуждения на случай большего числа уравнений можно провести аналогичным образом. Пусть требуется найти решение система линейных алгебраических уравнений (СЛАУ) вида:

(3.1)

Введем следующие обозначения:

, (3.2)

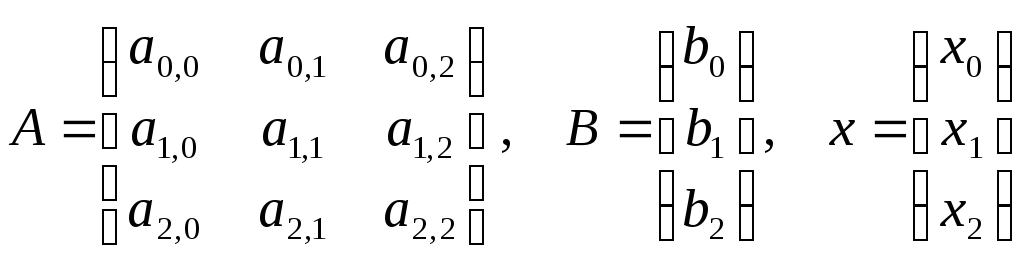
А – матрица коэффициентов;

В – вектор свободных членов;

х – вектор неизвестных.

В обозначениях (5.2) систему уравнений (5.1) можно записать в виде:

Из линейной алгебры известно, что система (3.3) имеет единственное решение при условии невырожденности матрицы, т.е. её детерминант должен быть отличным от нуля. Поэтому, какой бы вычислительный метод не применялся, решение системы линейных уравнений всегда нужно начинать с вычисления определителя (детерминанта) матрицы.

В разделе 6.4 мы уже рассматривали решение систем с использованием блока решения. Если применить к уравнению (3.3) аппарат матричных преобразований можно получить «матричную» формулу для вычисления x:

Помножим уравнение (3.3) слева на матрицу, обратную к матрице А:

. (3.4)

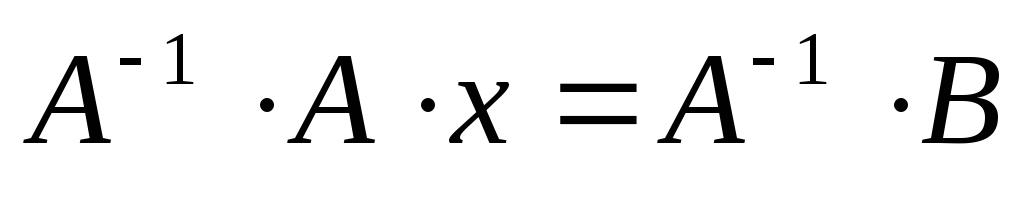
Воспользуемся свойством, что , гдеЕ – единичная матрица. Тогда уравнение (3.4) примет вид:

. (3.5)

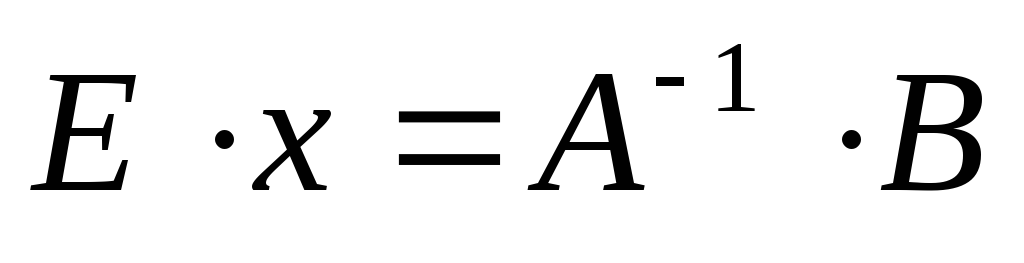
Воспользуемся свойством, что Ex = x. Тогда уравнение (3.5) примет вид:

, (3.6)

где (3.6) – решение системы (3.3).

Пример 15. Требуется найти решение следующей системы линейных уравнений:

Решение. Решение СЛАУ матричным способом в системе MathCAD приведено на рис.3.13.

Видео:Линал 2.6. Умножение матрицы на векторСкачать

Двумерный вектор в C++

Вектор используется для создания динамического массива, и размер вектора можно увеличивать и уменьшать, добавляя и удаляя элементы из вектора. Когда вектор объявляется внутри другого вектора, этот вектор называется 2-мерным вектором, который работает как 2-мерный массив. Двумерный вектор содержит несколько строк, каждая из которых является другим вектором. В этом руководстве показано использование двумерного вектора в C ++.

Синтаксис:

Синтаксис двумерного вектора приведен ниже.

Конкретный тип данных определяется во время объявления вектора. Если размер вектора не определен, вектор называется пустым вектором. Размер вектора можно изменить, используя различные методы или инициализируя вектор.

Видео:Ввод и вывод матриц в c++Скачать

Пример 1. Создайте двумерный вектор из равного количества столбцов

В следующем примере показан способ объявления двухмерного вектора из трех строк и четырех столбцов, который содержит символьные данные. Здесь значения вектора были определены в момент вектор декларации и вложенную » для » петли используется для печати значения вектора.

using namespace std ;
int main ( )
<
/*
Declare a two-dimensional vector
of characters
*/
vector vector > chrVector
< , , > ;
//Print the values of the vector
cout «The values of the vector are: n « ;
for ( int i = ; i chrVector. size ( ) ; i ++ )
<
for ( int j = ; j chrVector [ i ] . size ( ) ; j ++ )
cout chrVector [ i ] [ j ] » « ;
cout ‘ n ‘ ;
>
return ;
>

Следующий вывод появится после выполнения вышеуказанного кода.

Видео:#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy урокиСкачать

Пример 2: Создайте двумерный вектор с другим количеством столбцов

В следующем примере показан способ объявления двухмерного вектора из четырех строк, где первая строка содержит один столбец, вторая строка содержит два столбца, третья строка содержит три столбца, а четвертая строка содержит четыре столбца. Вектор инициализации с целым данных и распечатаны с помощью вложенной « для » петли.

using namespace std ;

int main ( )
<
/*
Initialize the 2D vector with the
integer number where each row contains different
number of elements
*/
vector vector > intVector
< , , , > ;
//Print the values of the vector using for loop
cout «The values of the vector are: n « ;
for ( vectorrow : intVector )
<
for ( int val : row )
cout val » « ;
cout ‘ n ‘ ;
>
return ;
>

Следующий вывод появится после выполнения вышеуказанного кода.

Видео:vector | Библиотека стандартных шаблонов (stl) | Уроки | C++ | #1Скачать

Пример 3: Инициализировать двумерный пустой вектор со значением по умолчанию

Способ объявления 2-мерного пустого вектора числа с плавающей запятой и инициализации вектора с числом с плавающей запятой показан в следующем примере. Здесь вложенный цикл for был использован для вставки данных в вектор с помощью функции push_back () и печати значений вектора.

Значение по умолчанию 6.5 было вставлено в вектор путем создания 2 строк и 3 столбцов. Функция size () использовалась для подсчета общего количества строк и столбцов для печати значений вектора.

using namespace std ;

int main ( )
<
//Set the default value
float default_value = 6.5 ;
//Define the outer vector
vector vector > outVect ;

for ( int i = ; i 2 ; i ++ )
<
//Define the inner vector
vectorinVect ;
for ( int j = ; j 3 ; j ++ ) <
//Insert the default value
inVect. push_back ( default_value ) ;
>
//Insert the inner vector to outer vector
outVect. push_back ( inVect ) ;
>

//Print the values of the vector
cout «The values of the vector are: n « ;
for ( int i = ; i outVect. size ( ) ; i ++ )
<
for ( int j = ; j outVect [ i ] . size ( ) ; j ++ )
cout outVect [ i ] [ j ] » « ;
cout ‘ n ‘ ;
>
return ;
>

Следующий вывод появится после выполнения вышеуказанного кода. Выходные данные показывают содержимое вектора на основе значения по умолчанию и количества строк и столбцов, созданных кодом.

Видео:Матрицы в Mathcad(создание и редактирование матриц)(Урок 3.1)Скачать

Пример 4: Инициализировать двумерный пустой вектор, принимая входные значения

В следующем примере показан способ создания двухмерного вектора, получая данные от пользователя. В коде объявлен двумерный пустой вектор целого числа, который будет содержать 2 строки и 3 столбца.

Вложенная » для » петли используется, чтобы принять 6 (2 × 3) целые числа от пользователя и вставить их в вектор с использованием значений индекса. Еще одна вложенная » для » петли была использовано для печати вставленных значений вектора.

using namespace std ;

int main ( )
<
//Define the number of cols
int col = 3 ;
//Define the number of rows
int row = 2 ;
//Initialize an integer variable
int val = ;
//Initialize the empty vector
vector vector > int2DVector ;

//Resize the outer vector
int2DVector. resize ( row ) ;
for ( int i = ; i row ; i ++ )
<
//Resize the inner vector
int2DVector [ i ] . resize ( col ) ;
for ( int j = ; j col ; j ++ )
<
//Take input from the user
cout val ;
//Insert into the vector
int2DVector [ i ] [ j ] = val ;
>
>

//Print the values of the vector
cout «The values of the vector are: n « ;
for ( int i = ; i int2DVector. size ( ) ; i ++ )
<
for ( int j = ; j int2DVector [ i ] . size ( ) ; j ++ )
cout int2DVector [ i ] [ j ] » « ;
cout ‘ n ‘ ;
>
return ;
>

Следующий вывод появится после выполнения вышеуказанного кода. Выходные данные показывают 6 входных значений и содержимое вектора в зависимости от количества строк и столбцов.

Видео:Матрицы и векторы. Создание матриц и основные операции с ними. Урок 11Скачать

Заключение

Двумерный вектор используется в программировании на C ++ для хранения и доступа к данным на основе строк и столбцов. В этом уроке на простых примерах были показаны различные способы создания двумерного вектора. Цель использования двумерного вектора в C ++ будет понятна после прочтения этого руководства.