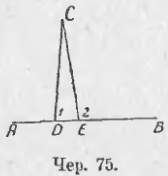- С применением циркуля
- С помощью линейки
- В остроугольном треугольнике
- В тупоугольной фигуре
- В прямоугольном и равнобедренном
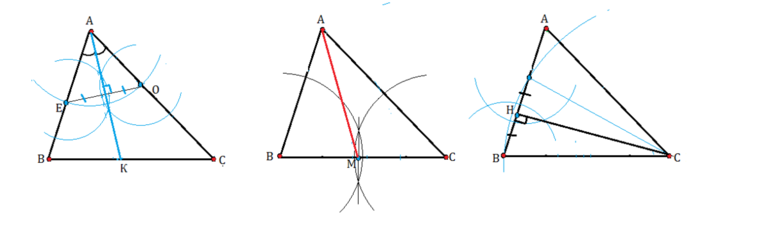
- Треугольник. Серединный перпендикуляр (медиатриса), средняя линия треугольника.
- Характерные особенности медиатрисы треугольника.
- Характерные особенности средней линии треугольника.
- Математика
- 🎥 Видео
Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

С применением циркуля
Если нужно нарисовать высоту (перпендикуляр к противоположной стороне) в произвольном треугольнике и измерить её, то лучше всего воспользоваться классическим методом построения. Он предусматривает использование циркуля в качестве основной рабочей принадлежности. Кроме этого, для работы понадобится лист бумаги, небольшая линейка, ластик и простой карандаш.
Способ начертить искомый отрезок:
- На листе бумаги чертят треугольник (можно нарисовать заранее, чтобы сэкономить время).
- Рисунок располагают так, чтобы вершина угла, из которого нужно начертить высоту, находилась сверху, а противоположная ему сторона фигуры была расположена горизонтально (по отношению к ученику).
- Иглу циркуля ставят в вершине любого угла у основания.
- Ножку с грифелем ставят в верхнюю точку треугольника, из которой проводится высота.
- Циркулем рисуют окружность и делают пометку в месте её пересечения с основанием фигуры.
- Аналогичным способом чертят круг из другого угла при основании. При этом важно определить новый радиус, который будет равен длине второй стороны треугольника.
- Делают пометку в месте пересечения начерченных окружностей.
- Ластиком стирают лишние линии, оставляя лишь поставленную точку.
- С помощью карандаша и линейки из неё проводят отрезок к вершине, который и будет высотой треугольника.
- Стирают линии, находящиеся под основанием.
Таким же способом можно с помощью циркуля построить высоту треугольника из любого другого угла.
Видео:Построение высоты в треугольникеСкачать

С помощью линейки
Начертить и обозначить высоту можно и без циркуля. Для этого следует воспользоваться чертёжным угольником, 2 стороны которого перпендикулярны друг другу. Альтернативой этой школьной принадлежности могут стать 2 прямые линейки, соединённые между собой под прямым углом.
В остроугольном треугольнике
Провести высоту в треугольнике, где все углы острые (менее 90 градусов), довольно просто.
Чтобы справиться с этой задачей, нужно подготовить все необходимое и заранее начертить на бумаге геометрическую фигуру.
Правильная последовательность действий:
- Находят вершину, из которой хотят провести перпендикуляр.
- Совмещают угольник с противоположной стороной фигуры.
- Перемещают чертёжную принадлежность до тех пор, пока её перпендикулярная сторона не пройдёт через вершину.
- Простым карандашом проводят линию, которая и будет искомым отрезком.
В тупоугольной фигуре
Трёхсторонняя фигура, у которой один из углов тупой (более 90 градусов) имеет только 1 внутреннюю высоту. Для её проведения используют то же, что и в предыдущем случае.
Порядок действий:
- Располагают чертёж так, чтобы тупой угол оказался у основания.
- Угольник прикладывают к наибольшей стороне фигуры.
- Совмещают перпендикулярную сторону линейки с вершиной тупого угла.
- Соединяют 2 точки простым карандашом, получая искомую линию.
В прямоугольном и равнобедренном
В прямоугольном треугольнике нужно находить только 1 высоту. Две другие будут совпадать с катетами.
Пошаговая инструкция:
- Прикладывают одну из перпендикулярных сторон угольника к гипотенузе.
- Вторую сторону линейки совмещают с вершиной прямого угла.
- Проводят линию, которая будет высотой.
Проще всего проводить перпендикуляр из верхней точки равнобедренного треугольника.
Он будет совпадать с биссектрисой и медианой фигуры. Начертить его можно таким же способом, что и для остроугольной фигуры. Более простой метод предусматривает выполнение следующих действий:
- Линейкой замеряют длину основания.
- Эту величину делят на 2.
- Полученное значение откладывают от вершины одного из углов при основании.
- Отмечают середину стороны и соединяют её с верхней точкой фигуры.
Проведение высоты в треугольнике — это простая задача, с которой легко справится каждый ученик.
Для этого достаточно сделать чертёж геометрической фигуры и воспользоваться одним из существующих способов построения. Такая работа потребует минимум времени и не отнимет у школьника много сил.
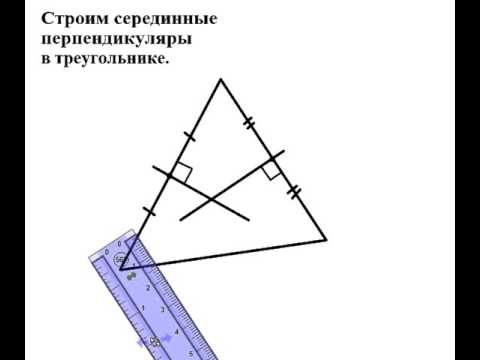
Видео:Построение серединных перпендикуляров треугольника с помощью циркуляСкачать

Треугольник. Серединный перпендикуляр (медиатриса), средняя линия треугольника.
Формулировка серединный перпендикуляр к отрезку или медиатриса звучит так — прямая, прочерченная через середину стороны под углом 90 0 .
Видео:Перпендикулярные прямые. 6 класс.Скачать

Характерные особенности медиатрисы треугольника.
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Правильна будут и такая формулировка: любая точка, равноудаленная от концов отрезка, размещена на серединном перпендикуляре к нему.
Центр описанной окружности находится в месте пресечения медиатрис треугольника. Следует отметить, что у остроугольного треугольника эта точка размещается внутри, у тупоугольного — за пределами треугольника, у прямоугольного — посредине гипотенузы.
Средняя линия трехугольника – отрезок, соединяющий середины двух его сторон. Общеизвестно, что у треугольника три стороны, и логично, что и три средние линии.
MN, MК, КN — средние линии для треугольника ABC.
Видео:Перпендикулярные прямыеСкачать

Характерные особенности средней линии треугольника.
Средняя линия трехугольника всегда параллельна одной из сторон и равна 1/2 этой стороны.
Средняя линия отделяет трехугольник, который подобен первоначальному, а их площади соотносятся ¼.
При пересечении всех трёх средних линий образуются четыре одинаковых треугольника, подобных первоначальному, но с коэффициентом подобия 0,5.
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Математика
68. В п. 63 мы научились строить прямой угол. Так как две прямые, составляющие прямые углы, называются перпендикулярными друг другу (п. 60), то построение п. 63 можно выразить словами иначе: мы можем построить прямую, перпендикулярную к данной.
Мы теперь должны эту общую задачу разобрать подробнее и прежде всего разделим ее на две отдельных задачи:
1) Дана прямая и точка на ней, построить чрез данную точку перпендикуляр к данной прямой. (Можно ли и сколько?).
2) Дана прямая и точка вне ее; построить чрез данную точку перпендикуляр к данной прямой. (Можно ил и сколько?).
В скобках указаны те вопросы, которые должны быть выяснены при выполнении построений.
69. 1-я задача . Дана прямая и точка на ней; построить чрез данную точку перпендикуляр к данной прямой.
Здесь остается повторить то построение, какое было дано в п. 63.
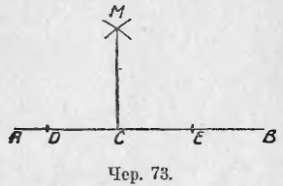
Пусть дана прямая AB и точка C на ней (чер. 73), построить чрез C перпендикуляр к AB.
От точки C откладываем по AB в разные стороны два произвольных, но равных отрезка CD = CE и затем, принимая последовательно точки D и E за центры, строим две окружности (или две дуги, достаточные для нахождения одной точки пересечения окружностей) одинаковыми радиусами, большими, чем отрезок CD. Точку пересечения M этих окружностей соединяем с C, тогда MC и есть искомый перпендикуляр, так как MC есть половина диагонали ромба, 3 вершины которого суть D, E и M.
Слово «перпендикуляр» пишут для сокращения знаком ⊥; мы построили
(CM перпендикуляр к AB).
Итак, выполнив это построение, мы можем признать, что чрез всякую точку, данную на прямой, можно построить к ней перпендикуляр (говорят иногда: восставить перпендикуляр к данной прямой). Остается еще вопрос: сколько?
Если луч CM повернуть около точки C в ту или другую сторону, то новые углы, составляемые этим лучом с прямою AB, уже не будут прямыми; поэтому заключаем, что возможно построить чрез точку прямой линии к этой прямой лишь один перпендикуляр .
70. 2-я задача . Дана прямая и точка вне ее; построить чрез данную точку перпендикуляр к данной прямой.
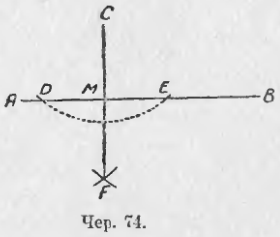
Пусть дана прямая AB и точка C вне ее (чер. 74); требуется чрез C построить перпендикуляр к AB.
Задача сводится к построению такого ромба, чтобы его одна вершина расположилась в точке C и одна его диагональ шла по прямой AB. Для построения такого ромба опишем, принимая C за центр, окружность (или дугу), выбрав ее радиус столь большим, чтобы эта окружность пересекалась с прямою AB; пусть она пересечет прямую AB в точках D и E. Тогда будут найдены еще две вершины ромба. Затем, принимая последовательно за центры точки D и E, построим два круга (или две дуги) тем же самым радиусом и найдем точку их пересечения, расположенную по другую сторону от прямой AB сравнительно с точкою C, пусть эта точка есть F. Тогда все 4 вершины ромба найдены; остается построить его диагональ CF, она, как мы знаем, и будет перпендикулярна к AB, т. е. CF ⊥ AB или CM ⊥ AB.
Стороны ромба DC, CE, EF и FD нет надобности строить.
Выполнив указанное построение, мы должны признать, что из всякой точки, данной вне прямой, мы можем построить перпендикуляр к данной прямой (говорят иногда: опустить перпендикуляр на данную прямую). Остается еще вопрос: сколько?
Для решения этого вопроса допустим, что чрез точку C (чер. 75) построено: 1) CD ⊥ AB и 2) CE ⊥ AB. Тогда ∠CDB или ∠1 и ∠CEB или ∠2 оба должны быть прямыми и, следов., равны между собою. Но ∠CEB есть внешний угол для ∆CDE, а мы знаем (п. 49), что внешний угол треугольника должен быть больше внутреннего с ним несмежного. Это противоречие показывает, что наше допущение не верно, т. е. Нельзя построить чрез точку C двух перпендикуляров к прямой AB. Итак:
Чрез точку, данную вне прямой, можно построить только один перпендикуляр к этой прямой .
Замечание . Если, как мы получили в этом п., CF ⊥ AB (чер. 74), то, очевидно, и AB ⊥ CF.
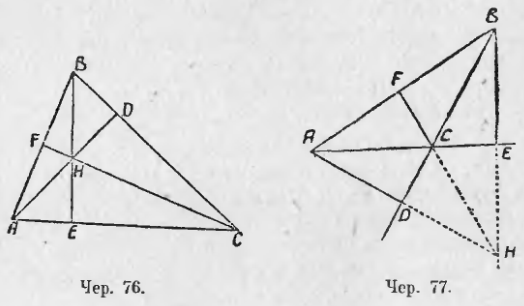
71. Построим какой-либо ∆ABC (чер. 76) и из каждой его вершины опустим перпендикуляр на противоположную сторону (здесь под именем сторона треугольника надо понимать бесконечную прямую). Каждый из этих перпендикуляров называется высотою треугольника. Следовательно, наша задача может быть выражена так: построить высоты треугольника. Если мы выполним построение перпендикуляров с возможною тщательностью, то в результате увидим, что по-видимому, все три высоты пересекаются в одной точке H, впоследствии мы выясним, что это свойство высот обязательно для всякого треугольника.
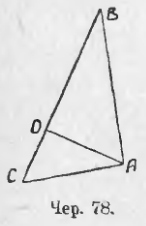
При построении высот может быть три случая: 1) все три высоты идут внутри треугольника (чер. 76); 2) две высоты BE и AD располагаются вне треугольника и общая точка H пересечения всех трех высот лежит вне треугольника (чер. 77) и 3) две высоты сливаются со сторонами треугольника (чер. 78), где BA ⊥ AC и CA ⊥ AB.
72. Для разбора вышеописанных трех случаев расположения высот условимся в обозначениях и названиях.
Прямой угол обозначают буквою d; тогда выпрямленный угол равен 2d, так как прямой угол есть половина выпрямленного угла. Если какой-либо угол больше прямого угла, то он называется тупым углом, а угол, меньший прямого угла, называется острым . Если ∠BAC (чер. 79) прямой, т. е., если ∠BAC = d, то ∠DAC > d и, следов., тупой, а ∠EAC сумма внутренних углов треугольника = 2d (или двум прямым углам ).
Ясно, что 3-й случай расположения высот в треугольнике, когда две его высоты сливаются со сторонами (чер. 78), имеет место, если ∠BAC треугольника прямой (∠BAC = d); такой треугольник с прямым углом называется прямоугольным . Так как сумма всех углов треугольника = 2d, а в этом случае ∠A прямой, или = d, то два другие угла (∠B и ∠C) в сумме составляют тоже прямой угол, а следовательно каждый из них в отдельности меньше прямого, или, другими словами, каждый из них острый угол.
Нетрудно теперь различать и два остальных случая: случай, данный на чер. 76, имеет место тогда, когда все 3 угла в треугольнике острые, а случай, данный на чер. 77, имеет место тогда, когда один из внутренних углов (на чер. 77 ∠BCA) тупой.
Ясно также, что если в треугольнике один угол тупой (или > d), то сумма двух других углов должна быть 1-й признак. Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого, то эти прямоугольные треугольники равны.
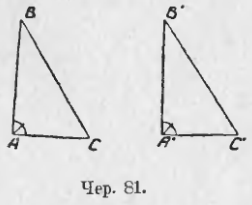
В самом деле это тот же самый признак, знакомый нам: если 2 стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого, то треугольники равны. Теперь про углы не говорится потому, что между катетами расположены прямые углы, а они всегда равны (на чер. 81). ∠A = ∠A’, как прямые, и достаточно для равенства ∆ABC и ∆A’B’C’ знать, что AB = A’B’ и AC = A’C’).
2-й признак. Если катет и прилежащий острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого, то эти прямоугольные треугольники равны.
Это опять-таки знакомый нам признак: если 2 угла и сторона между ними одного треугольника соответственно равны двум углам и стороне между ними другого треугольника, то эти треугольники равны. Теперь про равенство углов, прилегающих к равным катетам у другого конца каждого, не говорится, так как эти углы прямые, а они всегда равны (на чер. 81, где ∠A и ∠A’ прямые, достаточно для равенства треугольников знать, что AB = A’B’ и ∠B = ∠B’).
Можно вместо прилежащих углов к катетам взять углы, противолежащие этим катетам: если ∠C = ∠C’, то и ∠B = ∠B’, так как ∠B + ∠C = d и ∠B’ + ∠C’ = d.
Признак равенства треугольников по трем равным сторонам здесь нет нужды применять: мы уже знаем, что для равенства прямоугольных треугольников достаточно знать равенство двух сторон, а именно двух катетов (1-й признак).
3-й признак. Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого, то эти прямоугольные треугольники равны.
Этот признак является следствием общего признака: если 2 угла и сторона между ними одного треугольника соответственно равны двум углам и стороне между ними другого, то эти треугольники равны. В самом деле, пусть имеем 2 прямоугольных треугольника ABC и A’B’C’ (чер. 81), у которых BC = B’C’ и ∠С = ∠С’. Так как мы знаем, что ∠B + ∠C = d (сумма всех трех внутренних углов ∆ABC = 2d, но ∠A = d, следов., ∠B + ∠C = d) и ∠B’ + ∠C’ = d (ибо ∠A’ = d), а нам известно, что ∠C = ∠C’, то отсюда приходим к заключению, что ∠B = ∠B’ и тогда сторона BC и два прилегающих к ней угла ∠C и ∠B одного треугольника равны соответственно стороне B’C’ и двум прилегающим к ней углам другого ∠C’ и ∠B’, а мы знаем, что в этом случае ∆ABC = ∆A’B’C’.
4-й признак. Если гипотенуза и катет одного прямоугольного треугольника равны соответственно гипотенузе и катету другого, то такие прямоугольные треугольники равны.
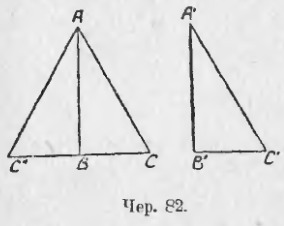
Этот признак удобнее всего выяснить следующим образом. Пусть имеем 2 прямоугольных треугольника ABC и A’B’C’ (чер. 82), причем ∠B = d и ∠B’ = d, у которых AC = A’C’ и AB = A’B’. Приложим ∆A’B’C’ и ∆ABC так, чтобы у них совпали равные катеты, т. е. A’B’ совпал бы с AB, и сами треугольники расположились бы по разные стороны от прямой AB, для этого иногда (напр., в случае, данном на чертеже) придется ∆A’B’C’ перевернуть другою стороною. Тогда сторона B’C’ должна пойти по такому направлению BC», чтобы ∠ABC» оказался прямым (ибо ∠B’ = d), а, следов., ∠CBC» оказался бы выпрямленным, т. е. Направление BC» должно быть продолжением стороны CB. Если точка C’ попадет в точку C», то, построив сторону AC», получим ∆ABC», равный ∆A’B’C’. Так как CBC» есть прямая линия, то получим еще ∆ACC», у которого сторона AC = AC», потому что AC» есть гипотенуза A’C’ треугольника A’B’C’, помещенного в положение ABC». Следовательно, ∆ACC» равнобедренный, а в таком случае углы при его основании равны, т. е. ∠C = ∠C», или ∠C = ∠C’. Оказалось, что у ∆ABC и ∠A’B’C’ имеется еще по равному острому углу, а в таком случае, на основании предыдущего признака, мы можем заключить, что ∆ABC = ∆A’B’C’.
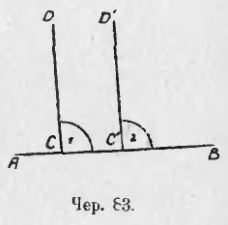
75. Пусть построено: 1) CD ⊥ AB и 2) C’D’ ⊥ AB (чер. 83); тогда, напр., ∠1 = ∠2, так как оба они прямые. Но эти углы суть соответственные при прямых CD и C’D’, пересеченных секущею AB, – следов., CD || C’D’.
Наоборот, пусть построено: 1) CD || C’D’ и 2) AB ⊥ CD (чер. 83); тогда AB должна пересечь и прямую C’D’ (п. 32, 1), напр. в точке C’. Легко увидим, что ∠2 = ∠1, так как эти углы соответственные при параллельных CD и C’D’ и секущей AB, но ∠1 = d, так как AB ⊥ CD, – следов., и ∠2 = d, т. е. AB ⊥ C’D’.
Поэтому имеем два заключения:
1) Два перпендикуляра к прямой параллельны.
2) Прямая, перпендикулярная к одной из параллельных, перпендикулярна и к другой.
76. Упражнения.
- Построить прямоугольный ∆ по катетам.
- Построить прямоугольный ∆ по катету и одному из острых углов.
- Построить прямоугольный ∆ по гипотенузе и острому углу.
- Построить прямоугольный ∆ по гипотенузе и катету.
- Построить высоты параллелограмма. Указать среди них равные.
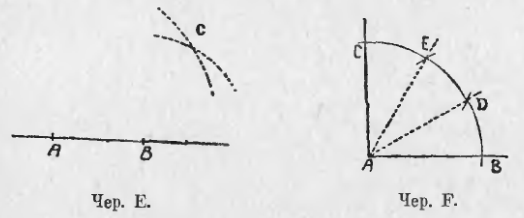
- Задачу «построить перпендикуляр к данной прямой чрез данную вне ее точку» можно решить следующим построением: на данной прямой берем 2 произвольных точки A и B (чер. E) и, принимая их последовательно за центры, построим два круга радиусами AC и BC, где C данная точка. Окончить это построение и выяснить его справедливость.
- Разделить прямой угол на 3 равных части.
Третью часть прямого угла легко построить: каждый внутренний угол равностороннего треугольника = 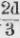
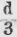
🎥 Видео
Серединные перпендикуляры в треугольникеСкачать
7 класс, 16 урок, Перпендикуляр к прямойСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Построение медианы в треугольникеСкачать

Перпендикуляр и наклонная в пространстве. 10 класс.Скачать

Построение биссектрисы в треугольникеСкачать

Наклонная, проекция, перпендикуляр. 7 класс.Скачать

8 класс, 36 урок, Свойства серединного перпендикуляра к отрезкуСкачать

6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Построение перпендикуляраСкачать

Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей | Математика | TutorOnlineСкачать

Параллельные прямые | Математика | TutorOnlineСкачать

Перпендикуляр к прямой через заданную точку.Скачать

№258. Из середины D стороны ВС равностороннего треугольника ABC проведен перпендикулярСкачать