Олимпиадные задачи на треугольники (8 видео)

Геометрия в 7 классе. Геометрия в задачах ОГЭ, ЕГЭ и олимпиад

Приведены олимпиадные задачи с решениями.

Содержание

Просмотр содержимого документа «Геометрия в 7 классе. Геометрия в задачах ОГЭ, ЕГЭ и олимпиад»
Геометрические задачи на этапе подготовки к олимпиадам
Геометрия треугольников. Задачи олимпиад.
Задания по теме для самостоятельного решения
Задание 1
Задание 2
Задание 3
🎬 Видео

Просмотр содержимого документа
«Геометрия в 7 классе. Геометрия в задачах ОГЭ, ЕГЭ и олимпиад»

Геометрия в 7 классе. Геометрия в задачах ОГЭ, ЕГЭ и олимпиад

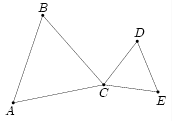
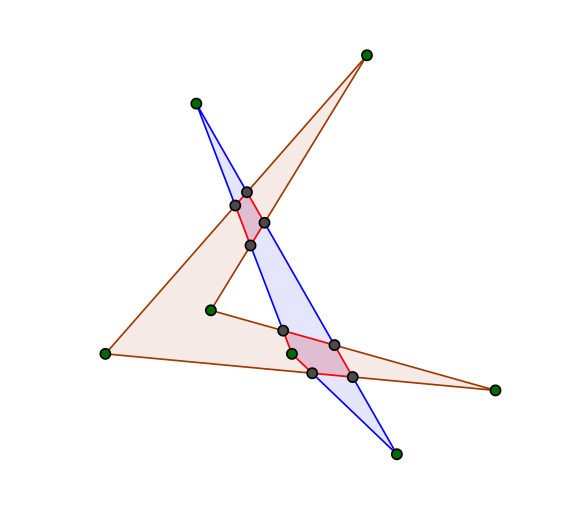
Два равносторонних треугольника ABC и CDE имеют общую вершину (см. рисунок). Найдите угол (в градусах) между прямыми AD и BE (углом между двумя пересекающимися прямыми называется наименьших из углов, образованных при пересечении)

Заметим, что треугольники ACD и BCE равны по первому признаку. Действительно, AC=BC, CD=CE и ∠DCA=60∘+∠BCD=∠ECA. Значит, ∠CAD=∠CBE. Тогда

Приведем набросок альтернативного рассуждения, которое тоже может быть оформлено в строгое решение (для этого см. тему «Движения плоскости»). Заметим, что при повороте вокруг точки C на 60 градусов точка E перейдет в точку D, а точка B перейдет в точку A. Значит, отрезок BE перейдет в отрезок AD. Потому и угол между ними равен 60 градусам.

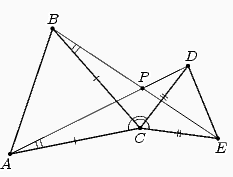
На основании AB равнобедренного треугольника ABC взята точка E, и в треугольники ACE и ECB вписаны окружности (касаются сторон треугольников ACE и ECB), касающиеся отрезка CE в точках M и N. Найдите длину отрезка MN, если AE=1и BE=3.

Обозначим через K и L точки касания окружности, вписанной в треугольник EBCсо сторонами EB и BC, соответственно.
Тогда заметим, что EC+EB−BC=EN+NC+EK+KB−CL−LB=EN+EK= поскольку CL=CN, BL=BK и EK=EN. Значит, EN=12(EC+EB−BC). Рассуждая аналогично, получаем, что EM=12(EA+EC−AC) Поэтому

Здесь третье равенство следует из того, что AC=BCAC=BC по условию.

Угол при вершине A треугольника ABC равен 120 o . Окружность касается стороны BC и продолжений сторон AB и AC. Докажите, что расстояние от вершины A до центра окружности равно периметру треугольника ABC.

Пусть D — точка касания окружности с прямой AB. Докажите, что отрезок AD равен полупериметру треугольника ABC.

Пусть O — центр окружности, D, E и F — точки касания с прямыми AB, BC и AC соответственно, 2p — периметр треугольника ABC. Тогда AD = AF, BE = BD и CE = CF. Поэтому

Поскольку луч AO — биссектриса угла DAC, то DAO = 60 o . Из прямоугольного треугольника ADO находим, что

На сторонах AB, BC и CA равностороннего треугольника ABC взяты точки C1, A1 и B1соответственно, причем так, что B1C1⊥AC, A1C1⊥AB, B1A1⊥BC. Найдите A1B:A1C.

Заметим, что все углы треугольника A1B1C1 равны по 60∘, так как ∠BA1C1=90∘−∠ABC=30∘, а ∠B1A1C1=180∘−∠BA1C1−∠B1A1C=60∘. Остальные углы вычисляются аналогично.

Следовательно, треугольник A1B1C1 равносторонний, откуда получаем, что △AC1B1=△BA1C1=△CB1A1 по катету (B1C1=C1A1=A1B1) и острому углу

Остается заметить, что поскольку ∠BA1C1=30∘, катет напротив этого угла вдвое меньше гипотенузы, то есть A1B=2BC1 причем BC1=CA1 ввиду равенства указанных выше трех прямоугольных треугольников. Отсюда следует, что A1B=2A1C.

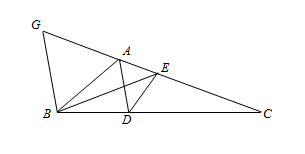
В треугольнике ABC проведены биссектрисы AD и BE. Известно, что DE – биссектриса угла ADC. Найдите градусную величину угла A.

Проведём через вершину B прямую, параллельную AD, до пересечения с прямой AC в точке G. Заметим, что ∠GBA = ∠BAD = ∠DAE = ∠BGC, то есть треугольник BAG равнобедренный (AB = AG). Как известно, биссектриса делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам. Применяя это свойство к биссектрисам DE и BE, получим DA : DC = AE : EC = BA : BC. Но DA : DC = BG : BC (треугольники ACD и GCB подобны). Значит, BA = BG и треугольник BAG – равносторонний. Поэтому ∠BAG = 60°.

Тимофей резал бумажный треугольник на кусочки (все разрезы — прямые). Сначала он разрезал этот треугольник на две части. Потом разрезал на два куска одну из полученных частей, и так далее. Когда ему надоело резать, оказалось, что общее количество углов у всех получившихся фигур равно 2015. Какое наименьшее количество разрезов мог сделать Тимофей?

При разрезании выпуклого многоугольника прямым разрезом получаются два многоугольника. При этом могут образоваться не более четырех новых углов, то есть, суммарное количество углов в образовавшихся многоугольниках превышает количество углов первоначального многоугольника не более, чем на 4. Поскольку 2015=3+503⋅4, то Тимофею хватит 503 разреза (а меньшего количества разрезов не хватило бы). Пример для 503 разрезов: достаточно каждый раз разрезать треугольник на треугольник и четырехугольник.

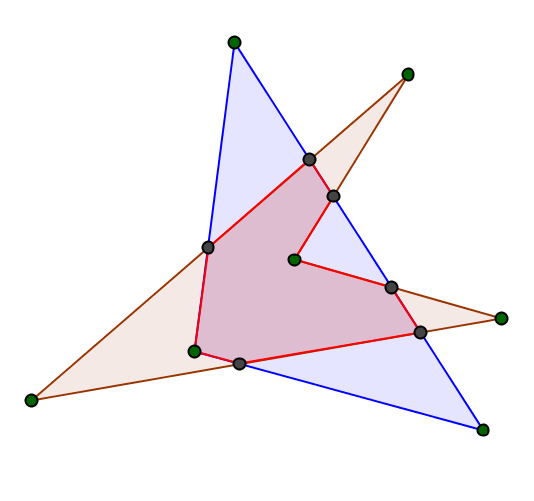
Какое наибольшее число сторон может иметь многоугольник, являющийся пересечением четырехугольника и треугольника?

Пример, когда в пересечении треугольника и четырехугольника получается восьмиугольник, см. ниже на картинке.

Оценка. Докажем, что в пересечении не может образоваться многоугольник с 9 или больше сторонами. Заметим, что каждая сторона треугольника не может пересекать внутренность четырехугольника больше двух раз (т.е. на стороне треугольника не может быть больше двух непересекающихся «участков», которые лежат внутри четырехугольника), в этом несложно убедиться перебором случаев (два раза сторона треугольника может пересекать внутренность четырехугольника, см. на картинке выше на самую длинную сторону). Аналогично, каждая сторона четырехугольника может пересекать внутренность треугольника не более одного раза (в этом тоже можно убедить простым перебором). Тогда для того, чтобы у пересечения треугольника и четырехугольника было по крайней мере 9 сторон, необходимо, чтобы две стороны треугольника пересекали внутренность четырехугольника два раза. Но нетрудно убедиться, что такое невозможно (тоже перебор случаев, ниже есть рисунок одной из возможных ситуаций), т.к. в этом случае в пересечении треугольника и четырехугольника будут получаться два многоугольника. Т.е. наибольшее число сторон у многоугольника, который образовался в пересечении треугольника и четырехугольника, равно 8.

Замечание 1. Если бы в условии задачи было сказано, что четырехугольник должен быть выпуклым, то ответ был бы равен 7.

Замечание 2. В 2013 году один из преподавателей центра онлайн-обучения «Фоксфорд» (а именно Кожевников Павел Александрович) опубликовал научную статью, в которой он доказал следующую теорему.

Если пересечение двух многоугольников (n1n1-угольника и n2n2-угольника) — многоугольник, то число сторон в нем не более

При этом существуют такие n1-угольник и n2-угольник, что их пересечением будет k-угольник.

Здесь [x]— целая часть числа x, т.е. наибольшее целое число, которое не превосходит xx. Например, [5,3]=5,[−0,5]=−1,[7]=7.

Доказательство данной теоремы достаточно непростое. Поэтому мы не будем разбирать его здесь. Но мы можем убедиться, что в статье получена точно такая же оценка как и в предложенном решении, поскольку в нашем случае (n1=3n1=3, n2=4n2=4):

Видео:Крутейшая олимпиадная задача и 3 её решенияСкачать

Геометрические задачи на этапе подготовки к олимпиадам

Статистика итогов математических олимпиад различного уровня показывает, что к решению геометрических задач приступают буквально единицы конкурсантов. Даже решение простых задач из школьного учебника вызывает затруднения у многих учащихся.
Чтобы приобщить учащихся к решению геометрических задач, убедить их в полезности таких занятий, необходимо уделять внимание разбору геометрических задач на уроках математики в 5 – 6 классах, на внеурочных занятиях, на этапе подготовки к олимпиадам.
Олимпиадные геометрические задачи полезны не только для проверки математических способностей и уровня математической подготовленности учащихся в жестких соревновательных условиях. На занятиях математического кружка, в спокойной обстановке, конкурсная задача является источником небольшого самостоятельного исследования, творческого открытия. Известный педагог-математик Д. Пойа писал: «Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия».
Необходимо как можно раньше начинать работать с детьми по развитию математических способностей, вызывать интерес к предмету, побуждать ребят к систематическим занятиям математикой. Поэтому я с 5 класса веду математический кружок, привлекаю учащихся к участию в олимпиадах и конкурсах различного уровня (школьный, районный тур олимпиад, республиканский этап математической олимпиады Junior math, международный математический конкурс «Кенгуру», различные интернет-олимпиады). Интересно, что ребята включаются в этот марафон, переживают за неудачи, радуются своим успехам, сравнивая предыдущие результаты с новыми и наблюдая «рост». Главное, разжечь в них соревновательный дух, который послужит важным стимулом к дальнейшим целенаправленным занятиям.
Для расширения кругозора и конструктивных навыков хороши практические задания, связанные с разрезаниями, проведениями построений. В таких задачах не используются знакомые алгоритмы решения, они требуют нестандартного подхода. Необходимо учить ребят находить пути к решению проблемы, а это значит – формировать у них способность к самостоятельному, творческому мышлению.
Представляю разработку кружкового занятия по теме «Решение геометрических задач». Занятие может быть организовано как для учащихся 5 – 6 классов, так и для более старших школьников. Главной целью его является приобщение учащихся к миру математики, убеждение учащихся в том, что размышление, рассуждение, выдвижение идей приводит к удивительным и полезным открытиям. Занятие построено так, что рассматривая задачи различного уровня и содержания, учащиеся постепенно, от простого к сложному, продвигаются в своем развитии, совершенствуют навыки решения олимпиадных задач. Разнообразные теоретические факты вытекают из практических упражнений и экспериментов. Это занятие составлено в соответствии с авторской модульной программой работы с математически способными детьми. Использованы задачи из различных сборников олимпиадных заданий:

Евдокимов М.А. От задачек к задачам. М.: МЦНМО, 2004
Игнатьев Е.И. В царстве смекалки. М.: «Наука», 1987
Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка. М.: «Просвещение», 1988
Материалы международного конкурса «КЕНГУРУ»

Методическая разработка занятия математического кружка

Класс:
5 – 6
Тема:
Решение геометрических задач

Цели:

развивать пространственное воображение, конструкторские навыки;
способствовать развитию интереса к предмету;
учиться ведению логически стройного доказательства;
способствовать самореализации и самосовершенствованию каждого ученика.

Оборудование:

карточки с заданиями;
наглядные иллюстрации к задачам;
сборники олимпиадных заданий;
материалы международного математического конкурса «КЕНГУРУ»;
бумага, ножницы для практических экспериментов.

Этапы занятия:

Организационные моменты (1 мин)
Разминка (5 мин)
Разбор интересных задач на проведение линий, разбиение фигур, перекраивания (20 мин)
Решение задач математического конкурса «Кенгуру» (15 мин)
Творческое домашнее задание (2 мин)
Подведение итогов занятия (2 мин)

Ход занятия:

1 этап. (Организационный)
Учитель: – Для работы разобьемся на группы, чтобы вам было интереснее работать с товарищами. Постарайтесь быть активными, полезными для своей команды. Вносите свои предложения, прислушивайтесь к мнению других.
(Класс разбивается на группы, в составе которых оказываются учащиеся с разной математической подготовкой. Это необходимо для того, чтобы каждый нашел себе применение, и «слабый» имел возможность тянуться за «сильным»)

II этап. Разминка
1) Учащиеся получают три рисунка:

Вопросы:
Сравните длины отрезков на рисунках 1 и 2. На сколько сантиметров один отрезок больше другого?
Сравните длины диагоналей параллелограммов на рисунке 3. У какого параллелограмма диагональ длиннее? (Для учащихся 5 – 6 классов пояснить, что называют параллелограммом, его диагоналями).
(После обсуждения в группах учащиеся высказывают предположения. Затем непосредственным измерением отрезков выясняют, правы ли они. Почему возникает такая иллюзия, что один отрезок кажется длиннее другого?)
2) Как, не отрывая карандаша от бумаги, разделить фигуру на рисунке 2 на шесть равных треугольников?

Рисунок 2. Рисунок 3. Рисунок 4.

III этап.Разбор интересных задач на проведение линий, разбиение фигур, перекраивания.
Задача 1
Постройте замкнутую ломаную линию, состоящую из трех звеньев и проходящую через четыре данные точки (Рисунок 3).
Задача 2
Как ломаной линией, состоящей из четырех отрезков, не отрывая карандаша от бумаги, перечеркнуть девять точек, расположенных так, как показано на рисунке 4?
(Обсудить все предложенные ребятами варианты решения. Обратить внимание учащихся на то, что задача считается решенной, если выполнены все требования условия, то есть ломаная состоит из четырех звеньев, звенья ломаной не должны накладываться друг на друга, линия должна быть без разрывов).
Задача 3
Как тремя прямолинейными разрезами разделить круглый торт на:
а) семь,
б) восемь частей (Рисунок 5)?

Возможные варианты решения (Рисунок 6, Рисунок 7):

Рисунок 6. Рисунок 7.

Задача 4

Как из набора «уголков» сложить прямоугольник (Рисунок 8)?
Решение:
Подсчитаем, какую площадь займут все «уголки» 3+4+5+6+7+8=11*3=33. Значит, стороны прямоугольника могут быть равны 3 и 11. Остается заполнить прямоугольник 3*11 данными «уголками». Например, как на рисунке 9:

Задача 5
Разрежьте фигуру на две части и сложите из них квадрат (Рисунок 10).

Вопросы для обсуждения:
– Какова площадь первоначальной фигуры?
12*9-8=108-8=100
– Значит, сложив части, мы получим квадрат размером 10*10.
– На сколько нужно увеличить сторону длиной 9 клеток и на сколько уменьшить другую сторону? (на 1 и на 2)
Вариант разрезания (Рисунок 11):

IV этап. Решение задач математического конкурса «Кенгуру»
Задачи «Кенгуру»

Решение: Заметим, что линия, составленная из горизонтальных и вертикальных отрезков, имеет наибольшую длину.
Сравним (Рисунок 13)

Таким образом, в порядке убывания длины: (D) – (C) – (A) или (E) – (B).
Самая короткая линия – В.
Для того, чтобы покрасить кубик, изображенный на левом рисунке (Рисунок 14), понадобится 9 кг краски. Сколько краски потребуется, чтобы покрасить фигуру, изображенную на правом рисунке?

(А) 4 кг (В) 5 кг (С) 6 кг (Д) 9 кг (Е) 12 кг
Решение: Площадь поверхности первой фигуры равна 9*6=54, правой – 9+9+9+5+5+5+12=54. Так как площади равны, то краски понадобится столько же, т.е. 9 кг.
Если бумажный кубик разрезать по некоторым ребрам и развернуть, то получится развертка I (Рисунок 15), а если стереть некоторые буквы и потом разрезать кубик иначе, получится развертка II. Какая буква стояла на месте вопросительного знака?

(A) А (B) В (C) С (D) Е (E) невозможно определить

Решение: «Соберем» первый (Рисунок 16) кубик и расставим на нем буквы (можно использовать модель кубика)

Рисунок 16. Рисунок 17.

Перевернем его на себя (Рисунок 17):
Если полученный кубик разрезать, то на месте вопросительного знака , то есть справа от D , будет буква Е.
Ответ: (D)
V этап.Творческое домашнее задание

У одной хозяйки было два клетчатых коврика: один размером 60х60 см, другой 80х80 см. Она решила сделать из них один клетчатый коврик размером 100х100 см. Мастер взялся выполнить эту работу и пообещал, что каждый коврик будет разрезан не более чем на две части и при этом не будет разрезана ни одна клетка. Обещание свое он сдержал. Как он поступил?
Изображенную на рисунке 18 фигуру требуется разделить на 6 частей, проведя всего лишь 2 прямые. Как это сделать?

VI этап. Подведение итогов занятия.

Узнали ли вы сегодня на занятии что-то новое? Что именно?
Понравилась ли вам работа в группах? Какую роль в группе играли вы? (Активно обсуждал, предлагал идеи, слушал других, старался не привлекать к себе внимания и т.п.)
Какие интересные элементы можно добавить в организацию занятия?

Ответы ребят помогут учителю оценить проведенное занятие, спланировать дальнейшую работу.

Видео:Решали пол-урока, а оказалось очень простоСкачать

Геометрия треугольников. Задачи олимпиад.

Олимпиадные задачи на свойства прямоугольных треугольников, неравенство треугольника, интересные геометрические задачи.

Видео:Олимпиадная задача четырех треугольниковСкачать

Задания по теме для самостоятельного решения

Задание 1

В равнобедренном треугольнике ABC угол B равен 30. AB=BC=6. Проведены высоты CD треугольника ABC и высота DE треугольника BDC. Найдите BE. В ответ запишите 2BE.