Как рассчитать расстояние между окружностями

Длина общей хорды двух окружностей вычисляется по формуле

Видео:Планиметрия 12 | mathus.ru | расстояние между центрами пересекающихся окружностейСкачать

Доказательства формул для длин общих касательных и общей хорды двух окружностей

Утверждение 1 . Если расстояние между центрами двух окружностей радиусов r₁ и r₂ равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле

что и требовалось доказать.

Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r₁ и r₂ равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле

что и требовалось доказать.

Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r₁ и r₂ равно d , то длина общей хорды AB этих окружностей вычисляется по формуле

Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3,

Видео:1 2 4 сопряжение окружностейСкачать

Ответ

Проверено экспертом

Уравнение окружности с центром (a;b) и радиусом R

центр окружности (-2;6) радиус 6

центр окружности (4;-5)радиус 5

по формуле расстояние между двумя точками :

находим расстояние между центрами заданных окружностей

Видео:Расстояние между центрами вписанной и описанной окружностей треугольника и их радиусами #ShortsСкачать

Разметка окружностей, центров и отверстий. Деление окружности на равные части и построение многоугольников

При разметке все построения производятся с помощью двух линий — прямой и окружности (на рис. 3.42 с целью повторения представлены элементы окружности).

Рис. 3.42. Окружность и ее элементы

Нахождение центра окружности. На плоских деталях, где уже имеются готовые отверстия, центр которых неизвестен, его находят геометрическим способом. На торцах цилиндрических деталей нахождение центра производят при помощи циркуля, рейсмуса, угольника-цетроискателя и колокола.

Разметка центра по угольнику-центроискателю. Разметку выполняют в следующей последовательности.

• 1. Деталь устанавливают на разметочную плиту так, чтобы размечаемый торец был сверху.
• 2. На торец цилиндрической детали накладывают угольник-центроиска- тель так, чтобы две его стороны (планки) касались цилиндрической поверхности детали, рис. 3.43.

Рис. 3.43. Нахождение центра окружности с помощью угольника-центроискателя

• 3. Левой рукой плотно прижимают линейку угольника к поверхности торца, а правой проводят чертилкой первую диаметральную риску.
• 4. Угольник-центроискатель поворачивают по цилиндрической поверхности детали примерно на 90° и проводят вторую риску. Точка пересечения двух рисок будет центром размечаемой окружности.

Разметку центра детали с грубо обработанной цилиндрической поверхностью производят в такой же последовательности. В этом случае для более точного нахождения центра окружности необходимо нанести пять-семь рисок. Центром будет точка, в которой пересекается наибольшее число рисок.

Точность разметки центра окружности проверяют разметочным циркулем, рис. 3.44. Острие одной ножки циркуля устанавливают в размеченный центр, а другую ножку перемещают так, чтобы ее острие слегка касалось цилиндрической части детали. Если острие ножки циркуля касается по всей длине окружности, то центр размечен правильно.

Рис. 3.44. Способ проверки точности разметки центра окружности разметочным циркулем

Разметка центра рейсмусом (рис. 3.45). Деталь кладут на призмы или параллельные подкладки, уложенные на разметочную плиту. Устанавливают острый конец иглы рейсмуса несколько выше или ниже центра размечаемой

Рис. 3.45. Разметка центра рейсмусом

детали и, придерживая деталь левой рукой, правой рукой движением рейсмуса по плите прочерчивают его иглой на торце детали короткую рису. После этого поворачивают деталь на 1/4 окружности и таким же способом проводят вторую риску. То же повторяют через каждую четверть оборота для проведения третьей и четвертой рисок. Внутри рисок (на пересечении диагоналей) и будет находиться центр. Его набивают кернером.

Геометрический способ нахождения центра заключается в следующем. Пусть дана плоская металлическая плита с готовым отверстием, центр которого неизвестен. Перед тем как начать разметку, вставляют в отверстие широкий деревянный брусок и на него набивают пластинку из белой жести или из оцинкованного кровельного железа.

Затем на краю отверстия слегка намечают произвольно три точки Л, В и С и из каждой пары этих точек ЛВ и ВС описывают по обе стороны их пересекающиеся между собой дуги-засечки 1—2 и 3—4, рис. 3.46. Через точки пересечения дуг проводят две прямые по направлению к центру до их пересечения в точке О. Точка пересечения этих прямых, и будет искомым центром отверстия.

Рис. 3.46. Нахождение центра геометрическим способом

Разметка центра циркулем (кронциркулем). Зажав деталь в тиски, растворяют ножки циркуля на величину, немного большую или немного меньшую радиуса размечаемой детали. После этого, приложив к боковой поверхности детали одну ножку циркуля и придерживая ее большим пальцем, другой ножкой циркуля очерчивают дугу. Далее переместив циркуль на 1/4 окружности (на глаз), таким же образом очерчиваю вторую дугу. Затем через каждую четверть окружности очерчивают третью и четвертую дуги. Затем соединить противоположные засечки диагоналями, рис. 3.47я. Центр окружности будет находиться внутри очерченных дуг на пересечении диагоналей.

Рис. 3.47. Разметка центра циркулем (кронциркулем)

Можно разметить центр и способом, показанным на рис. 3.476. Методика разметки аналогична разметке рейсмусом.

Разметка центра колоколом. Приспособление колокол устанавливается на торец цилиндрической детали. Придерживая колокол левой рукой в вертикальном положении, правой рукой наносят удар молотком по кернеру, находящемуся в колоколе, рис. 3.48. Кернер сделает углубление в центре торца.

Рис. 3.48. Разметка центра колоколом

Деление окружности на равные части. При разметке окружностей часто приходится их делить на несколько равных частей — 3, 4, 5, 6, и больше. Ниже приведены примеры деления окружности на равные части геометрическим способом и с помощью таблиц.

Деление окружности на три равные части с построением вписанного треугольника (рис. 3.49).

Рис. 3.49. Деление окружности на три части с построением вписанного треугольника

• 1. В центре размечаемой плоскости с помощью циркуля проводим окружность требуемого радиуса, например R = 26 мм.
• 2. Через центр окружности по линейке проводим прямую риску с пересечением окружности в точках А и В.
• 3. Опорную ножку циркуля устанавливаем в точку А и при растворе циркуля, равном радиусу проведенной окружности, делаем на окружности две метки-засечки (точки С и D), где длина дуги между ними будет равна одной трети длины окружности.
• 4. Соединив точки прямыми рисками СД СВ и BD, получим вписанный равносторонний треугольник.
• 5. Правильность построения проверяем циркулем, устанавливая раствор циркуля равным одной из сторон треугольника и этим же размером определяя равенство остальных сторон треугольника.

Деление окружности на четыре равные части с построением вписанного квадрата, рис. 3.50.

Рис. 3.50. Деление окружности на четыре части с построением вписанного квадрата (а) и прием разметки квадрата (6)

• 1. В центре размечаемой плоскости циркулем проводим окружность требуемого радиуса, например R= 28 мм.
• 2. Через центр окружности по линейке проводим прямую риску что бы она пересекала окружности в двух точках А и В и разделяла ее на две равные части.
• 3. Опорную ножку циркуля устанавливаем в точку А и, раздвинув циркуль на расстояние несколько большее, чем половина отрезка АВ, проводим дугу в.
• 4. Опорную ножку циркуля переносим в точку В и, не изменяя раствора циркуля, проводим дугу б так, чтобы она пересекла первую выполненную дугу в точках 7 и 2.
• 5. Через точки 7 и 2 проводим риску, которая образует на окружности точки С и D.
• 6. Соединив точки AD, DB, ВС и СА прямыми рисками, получим квадрат, вписанный в окружность.

Деление окружности на пять равных частей (рис. 3.51). На данной окружности проводим два взаимно перпендикулярных диаметра, пересекающие окружность в точках А и В, С и D. Радиус ОА делим пополам и из полученной точки Е описываем дугу радиусом ЕС до пересечения в точке F на радиусе О В. После этого соединяем прямой точки D и F. Откладывая длину прямой DF по окружности, разделим ее на пять равных частей.

Деление окружности на шесть равных частей с построением вписанного шестиугольника, рис. 3.52.

Рис. 3.51. Деление окружности на пять равных частей

Рис. 3.52. Деление окружности на шесть частей с построением вписанного шестиугольника

• 1. В центре разметочной плоскости циркулем проводим окружность требуемого радиуса, например 7? = 27 мм.
• 2. Через центр окружности по линейке проводим прямую риску с пересечением окружности в точках А и В.
• 3. Из точки А, как из центра, наносим дугу радиусом, равным радиусу проведенной окружности, и получаем точки 7 и 2

Аналогичное построение делаем из точки В, нанося точки 3 и 4. Полученные точки пересечения и концевые точки диаметра будут искомыми точками деления окружности на шесть частей.

4. Соединив точки прямыми рисками А — 1,2 — 4, 4 — В, В — 3, 3 — 1 и 1 — А, получим вписанный шестиугольник.

При разметке граней шестиугольника под размер h зева гаечного ключа (рис. 3.53) радиус описываемой окружности определяется по формуле R = 0,577/г.

Рис. 3.53. Пример разметки шестиугольника под размер зева гаечного ключа

Деление окружности на равные части с помощью таблицы. Эта таблица (табл. 3.5) имеет две графы: «Число делений окружности» и «Число, умножаемое на радиус окружности». Числа первой графы показывают, на сколько равных частей следует делить данную окружность. Во второй графе даны числа, на которые умножают радиус данной окружности. В результате умножения числа, взятого из второй графы, на радиус размечаемой окружности получаем величину хорды, т. е. расстояние по прямой между делениями окружности.

Таблица 3.5. Деление окружности на равные части

📽️ Видео

Найти расстояние между центрами описанной и вписанной окружностей в прямоугольном треугольникеСкачать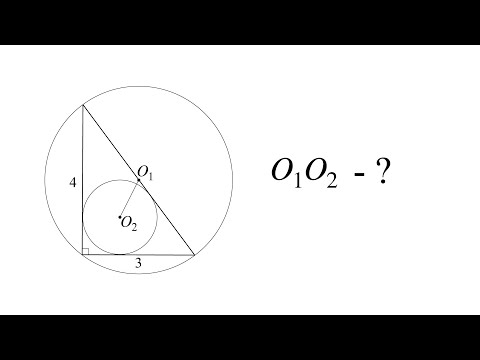

Всё про углы в окружности. Геометрия | МатематикаСкачать

Расстояние между параболой и окружностьюСкачать

Планиметрия 11 |mathus.ru|  расстояние между центрами пересекающихся окружностейСкачать

Уравнение окружности (1)Скачать

Как искать точки на тригонометрической окружности.Скачать

Планиметрия 5 | mathus.ru | расстояние между центрами окружностей в параллелограммеСкачать

Длина окружности. Площадь круга. 6 класс.Скачать

9 класс, 6 урок, Уравнение окружностиСкачать

М1152. Расстояние между центрами вписанной и описанной окружностейСкачать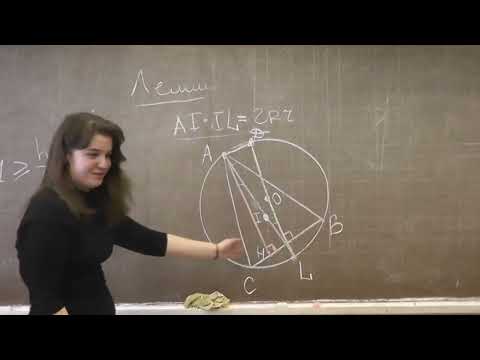

Длина отрезкаСкачать

Деление окружности на 3; 6; 12 равных частейСкачать

Длина окружности. Математика 6 класс.Скачать

Сможешь найти расстояние между центрами пересекающихся окружностей?Скачать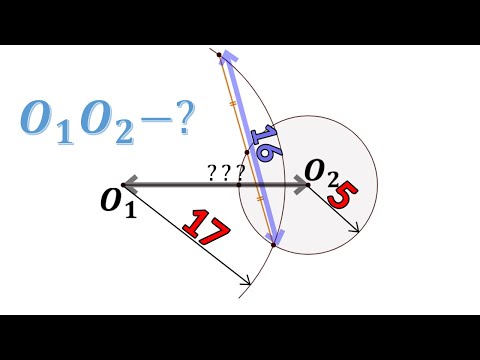