Как правильно вписать десятиугольник в окружность

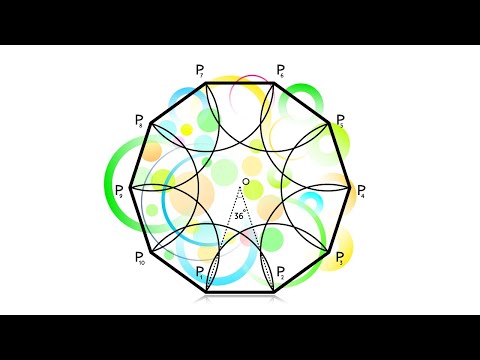
Десятиугольник, вписанный в окружность

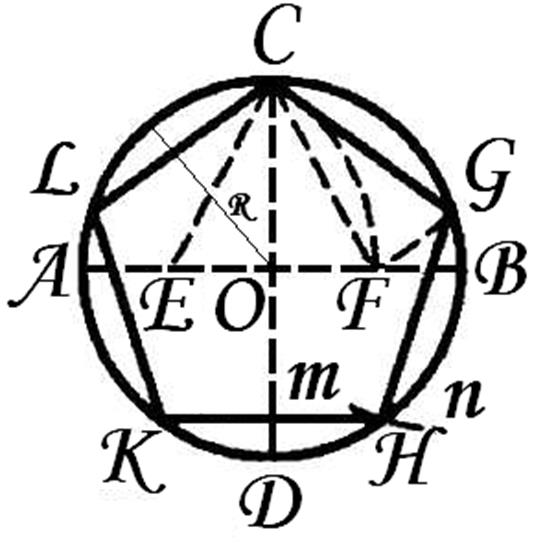
Проводим два взаимно перпендикулярных диаметра АВ и CD. Делим пополам радиус АО в точке Е. Из Е радиусом ЕС проводим дугу CF, пересекая ею диаметр АВ в точке F. OF есть сторона искомой фигуры. С помощью циркуля, сделаем на окружности десять последовательных засечек. Получим вершины искомой фигуры. Подобно построению пятиугольника, вписанного в окружность.

Десятиугольник, описанный около окружности

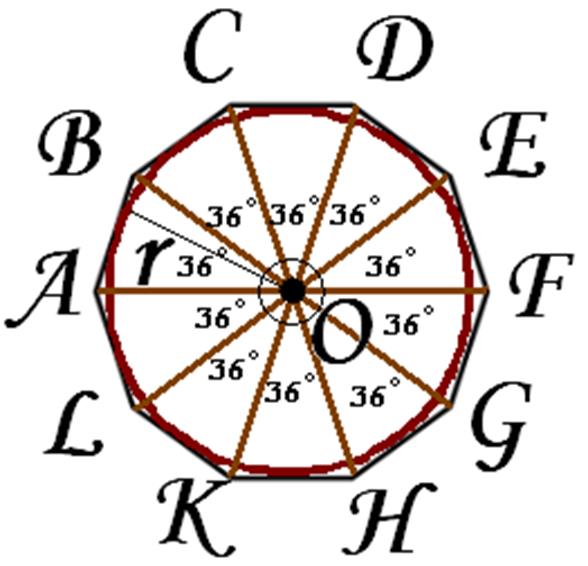
Имеем исходную окружность с центром в точке O. Так как сумма углов, составляющих центральный угол окружности, равна 360°. Делим данный угол на 10 частей (т.к. строим десятиугольник) с помощью транспортира, т.е. 360°:10=36°. Получаем 10 вершин: A, B, C, D, E, F, G, H, K, L. Соединяем эти вершины, получаем правильный десятиугольник.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Сдача сессии и защита диплома – страшная бессонница, которая потом кажется страшным сном. 8924 – | 7231 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

• Как начертить десятиугольник
• Как начертить угол без транспортира
• Как построить правильный восьмиугольник

• – циркуль;
• – линейка.

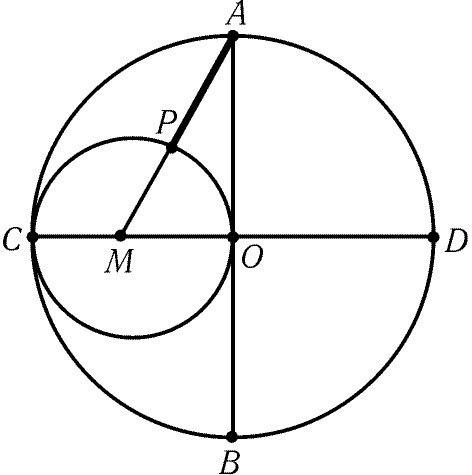
2 способ: Опять же, с помощью циркуля начертите окружность. Центр получившейся окружности обозначьте буквой О. Проведите два перпендикулярных диаметра данной окружности СD и АВ. Разделите один из 4-х радиусов на две равные части. Из рисунка видно, что радиус СО = СМ+МО, где СМ=МО.

Дальше поставьте ножку циркуля в точку М и начертите окружность радиусом, равным половине радиуса первоначальной окружности. С помощью линейки соедините центр маленькой окружности М с любой из 2-х точек (А или В) на перпендикулярном диаметре. На рисунке центр маленькой окружности соединен сточкой А. Длина, получившегося отрезка АМ будет равна длине стороны десятиугольника. Осталось только сделать раствор циркуля, равный длине отрезка АМ, поставить ножку циркуля в точку А и отметить следующую точку на окружности. Далее переместите ножку циркуля в новую точку и отметьте следующую. И так до тех пор, пока на окружности не появится 10 равноудаленных друг от друга точек.

Правильный десятиугольник
Сторон и вершин	10
Символ Шлефли
Внутренний угол	144°
Симметрия	Диэдрическая ( D 10 > ), порядок 20.

Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами и десятью сторонами.

Видео:ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]Скачать

Содержание

Видео:Построение пятиугольника циркулем и линейкойСкачать

Правильный десятиугольник [ править | править код ]

У правильного десятиугольника все стороны равной длины, и каждый внутренний угол составляет 144°.

Площадь правильного десятиугольника равна (t — длина стороны):

A = 5 2 t 2 c t g π 10 = 5 t 2 2 5 + 2 5 ≈ 7.694 t 2 . >t^ ctg >= > > >>>approx 7.694t^ .>

Альтернативная формула A = 2.5 d t , где d – расстояние между параллельными сторонами или диаметр вписанной окружности. В тригонометрических функциях он выражается так:

d = 2 t ( cos ⁡ 3 π 10 + cos ⁡ π 10 ) , >+cos >
ight),>

и может быть представлен в радикалах как

d = t 5 + 2 5 . >>>.>

Сторона правильного десятиугольника, вписанного в единичную окружность, равна 5 − 1 2 = 1 φ >-1> >= >> , где φ – золотое сечение.

Радиус описанной окружности десятиугольника равен

R = 5 + 1 2 t , >+1> >t,>

а радиус вписанной окружности

r = 5 + 2 5 2 t . >>> >t.>

Построение [ править | править код ]

По теореме Гаусса — Ванцеля правильный десятиугольник возможно построить, используя лишь циркуль и линейку.

Иначе его можно построить следующим образом:

1. Построить сначала правильный пятиугольник.
2. Соединить все его вершины с центром описанной окружности прямыми до пересечения с этой же окружностью на противоположной стороне. В этих точках пересечения и находятся остальные пять вершин десятиугольника.
3. Соединить по порядку вершины пятиугольника и пять точек, найденные шагом ранее. Искомый десятиугольник построен.

Видео:Построение пятиугольника циркулемСкачать

Разбиение правильного десятиугольника [ править | править код ]

Гарольдом Коксетером было доказано, что правильный 2 m -угольник можно разбить на m ( m − 1 ) 2 >> ромбов. Для декагона m = 5 , так что он может быть разбит на 10 ромбов.

Видео:Построение 7 угольника циркулем, приближенноеСкачать

Пространственный десятиугольник [ править | править код ]

Правильные пространственные десятиугольники
#	#	#

Пентаграммная антипризма с перекрёстом

Пространственный десятиугольник — это пространственный многоугольник с десятью рёбрами и вершинами, но не лежащими в одной плоскости. У пространственного зиг-заг десятиугольника вершины чередуются между двумя параллельными плоскостями.

У правильного пространственного десятиугольника все рёбра равны. В трёхмерном пространстве это зиг-заг пространственный декагон, он может быть обнаружен среди рёбер и вершин пентагональной антипризмы, пентаграммной антипризмы, пентаграммной перекрещивающейся антипризмы с той же D_5d [2 + ,10] симметрией порядка 20.

Его также можно найти в некоторых выпуклых многогранниках с икосаэдрической симметрией. Многоугольники по периметру этих проекций (см. ниже) это пространственные десятиугольники.

Ортогональные проекции многогранников
Додекаэдр	Икосаэдр	Икосододекаэдр	Ромботриаконтаэдр

Многоугольники Петри [ править | править код ]

Правильный пространственный десятиугольник — это многоугольник Петри для многих многогранников высших размерностей, как показано на этих ортогональных проекциях на различных плоскостях Коксетера.

Видео:Построение пятиугольникаСкачать

Построение правильных многоугольников. Решение задач

Разделы: Математика

Цели урока: закрепить знание формул стороны и площади правильного многоугольника, совершенствовать навык построения правильных многоугольников, научить строить правильный десятиугольник и правильный пятиугольник.

1. Проверка домашнего задания: пункт 108, №№ 1081, 1093, 1094(а,б).

Учебник Геометрия 7 — 9, Л.С. Атанасян.2003г.

а) = 180 = 60

б) = 180 = 3 · 36

в) = 180 = 120

г) = 180 = 144

д) = · 180 = 160

Дано: АВС — правильный

Окр.(О;R) — описана около АВС

Окр.(О;r) — вписанна в АВС

1. АО — биссектриса А OАD = 30

2. AOD — прямоугольный, т.к. OD = r проведён в точку касания (теорема о касательной к окружности).

3. В прямоугольном AOD катет r лежащий против угла в 30 равен половине гипотенузы R, т.е. R = 2r — ч.т.д.

Задача № 1094(а,б) (данное задание на закрепление знания формул:

S = Рr, a_n = 2R, r = R )

a₄ = 2R = 2 * 3 * = 2 * 3* = 6 см,

r = 3 * = 3 * = 3 см,

S = Рr = · 24 · 3 = 36 см 2

б) Решение: a₃ = = 8 см

Выразим r через a_n : r = ( a_n * ctg)/2

r = 4* ctg = см

S = (1/2)Рr = 16 см 2 Ответ: 16 см 2 .

2. Актуализация знаний учащихся (устный опрос):

1. Какой многоугольник называется правильным?

2. Какая окружность называется вписанной в многоугольник?

3. По какой формуле можно найти сторону правильного n-угольника? (записать на доске)

4. Какая точка называется центром правильного многоугольника?

5. Можно ли найти площадь правильного шестиугольника, зная только радиус вписанной в него окружности? Как это сделать? (показать на доске)

3. Изучение нового материала.

Строить правильные треугольники и четырёхугольники с помощью циркуля и линейки мы уже умеем. Рассмотрим способ построения правильного шестиугольника.

Задача № 1 из п.109 (работа с учебником).

Построить правильный шестиугольник, сторона которого равна данному отрезку.

1. Строим окружность радиусом R равным данному отрезку.

2. На окружности произвольно выбираем точку A₁ .

3. Не меняя раствора циркуля, на окружности откладываем точку A₂ , так чтобы A₁A₂ = R.

4. Аналогично от точки A₂ откладываем точку A₃ и т. д. до точки A₆ .

5. Соединяя последовательно построенные точки отрезками, получаем искомый правильный шестиугольник .

Доказательство: (можно провести устно)

1. Стороны 6 — угольника равны (по построению). (*)

2. О A₁A₂ = О A₂A₃ = О A₃A₄ = : = О A₆A₁ — по третьему признаку равенства -ов.

Все они равносторонние. A₁A₂A₃ = : = A₆A₁A₂ = 120° (**)

3. Из (*) и (**) A₁A₂A₃A₄A₅A₆ — правильный 6 — угольник — ч.т.д.

11Задача № 1279. На рисунке 370 изображён правильный десятиугольник, вписанный в окружность радиуса R, АС — биссектриса угла ОАВ. Докажите, что:

а) AВС

ОАВ

б) АВ = АС = ОС = R

(т.к. данная задача является задачей повышенной трудности, то перед решением её у доски необходимо дать учащимся две — три минуты на обдумывание, если не будет идей, то задавать наводящие вопросы.)

1. Рассмотрим равнобедренный ОАВ:

АО и ВО — биссектрисы углов правильного десятиугольника ( = 144)

Следовательно: = = 72, а значит = 36.

2. = 72, а т.к. АС — биссектриса этого угла, то = 36, т.е. = (*)

3. — общий для AВС и ОАВ. (**)

4. Из (*) и (**) следует (по первому признаку подобия треугольников),

что AВС

ОАВ — ч.т.д.

б) 1. В AВС: = 36, = 72 = 72, значит АВ = АС.

2. В ОАС: = = 36 АС = ОС

3. Обозначим АВ через х, ОС также равно х. АО = R , BC = R — x .

Из подобия AВС и ОАВ следует: x 2 + Rх — R 2 = 0

(получили квадратное уравнение относительно х)

x₁ = — решений нет, т.к. длина отрезка не может быть отрицательной

x₂ = = R — ч.т.д.

Исследование: зададимся вопросом — чему равен и .

1. В ОАВ проведём медиану ОК (она же высота и биссектриса).

АК = x/2= R·

R = R·

Итак: =

2. = 2* = 2* * = · = = =

=

11Задача № 1280. Докажите, что отрезок АК, изображённый на рисунке, равен стороне правильного десятиугольника, вписанного в окружность с центром О.

А и В Окр(О;R);

АООВ;

Окр(С; r = СВ)АС = К

Доказать: АК = R (по предыдущей задачи)

1. АО = R, OC = , AC = = ;

2. КС = , АК = АС — КС = — = R — ч.т.д.

Вывод: данный способ можно использовать для построения правильного десятиугольника.+

4. Закрепление изученного материала.

Задача № 1283: В данную окружность впишите правильный пятиугольник.

Мы рассмотрим иной способ построения, не тот который предлагают в ответе.

1. Строим окружность произвольного радиуса R и проводим два взаимно перпендикулярных диаметра АВ и СD.

2. Делим пополам радиус АО точкой Е.

3. Из Е радиусом ЕС проводим дугу CF, пересекая ею диаметр АВ в точке F.

4. Из С радиусом CF проводим дугу FG, пересекая ею данную окружность в точке G; CG(равная CF) есть одна сторона искомой фигуры.

5. Проводим тем же радиусом дугу из точки G как из центра, получаем ещё одну вершину Н искомой фигуры и т. д.

6. CGHKL — правильный пятиугольник.

1. Сторона правильного пятиугольника вписанного в Окр.(О;R) равна .

11 ОМ — биссектриса, медиана и высота равнобедренного ОСG.

СМ = R a₅ = 2СМ = 2 R

Учитывая, что = ,

окончательно получаем: a₅ = .

2. У нас по построению

1) ЕО = ; ЕС = ЕF =

2) OF = EF — EO = R

3) CG = CF = = = .

Итак, по построению CG = — ч.т.д.

5. Подведение итогов урока.

Домашнее задание: пункт 109, № 1282, №1284.

Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Как вписать десятиугольник в окружность

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

10 Угольник вписанный в окружность

Десятиугольник, вписанный в окружность

Проводим два взаимно перпендикулярных диаметра АВ и CD. Делим пополам радиус АО в точке Е. Из Е радиусом ЕС проводим дугу CF, пересекая ею диаметр АВ в точке F. OF есть сторона искомой фигуры. С помощью циркуля, сделаем на окружности десять последовательных засечек. Получим вершины искомой фигуры. Подобно построению пятиугольника, вписанного в окружность.

Десятиугольник, описанный около окружности

Имеем исходную окружность с центром в точке O. Так как сумма углов, составляющих центральный угол окружности, равна 360°. Делим данный угол на 10 частей (т.к. строим десятиугольник) с помощью транспортира, т.е. 360°:10=36°. Получаем 10 вершин: A, B, C, D, E, F, G, H, K, L. Соединяем эти вершины, получаем правильный десятиугольник.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Сдача сессии и защита диплома – страшная бессонница, которая потом кажется страшным сном. 8924 – | 7231 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

• Как начертить десятиугольник
• Как начертить угол без транспортира
• Как построить правильный восьмиугольник

• – циркуль;
• – линейка.

2 способ: Опять же, с помощью циркуля начертите окружность. Центр получившейся окружности обозначьте буквой О. Проведите два перпендикулярных диаметра данной окружности СD и АВ. Разделите один из 4-х радиусов на две равные части. Из рисунка видно, что радиус СО = СМ+МО, где СМ=МО.

Дальше поставьте ножку циркуля в точку М и начертите окружность радиусом, равным половине радиуса первоначальной окружности. С помощью линейки соедините центр маленькой окружности М с любой из 2-х точек (А или В) на перпендикулярном диаметре. На рисунке центр маленькой окружности соединен сточкой А. Длина, получившегося отрезка АМ будет равна длине стороны десятиугольника. Осталось только сделать раствор циркуля, равный длине отрезка АМ, поставить ножку циркуля в точку А и отметить следующую точку на окружности. Далее переместите ножку циркуля в новую точку и отметьте следующую. И так до тех пор, пока на окружности не появится 10 равноудаленных друг от друга точек.

Правильный десятиугольник
Сторон и вершин	10
Символ Шлефли
Внутренний угол	144°
Симметрия	Диэдрическая ( D 10 > ), порядок 20.

Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами и десятью сторонами.

Видео:Построение 10 угольника циркулемСкачать

Содержание

Видео:9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

Правильный десятиугольник [ править | править код ]

У правильного десятиугольника все стороны равной длины, и каждый внутренний угол составляет 144°.

Площадь правильного десятиугольника равна (t — длина стороны):

A = 5 2 t 2 c t g π 10 = 5 t 2 2 5 + 2 5 ≈ 7.694 t 2 . >t^ ctg >= > > >>>approx 7.694t^ .>

Альтернативная формула A = 2.5 d t , где d – расстояние между параллельными сторонами или диаметр вписанной окружности. В тригонометрических функциях он выражается так:

d = 2 t ( cos ⁡ 3 π 10 + cos ⁡ π 10 ) , >+cos >
ight),>

и может быть представлен в радикалах как

d = t 5 + 2 5 . >>>.>

Сторона правильного десятиугольника, вписанного в единичную окружность, равна 5 − 1 2 = 1 φ >-1> >= >> , где φ – золотое сечение.

Радиус описанной окружности десятиугольника равен

R = 5 + 1 2 t , >+1> >t,>

а радиус вписанной окружности

r = 5 + 2 5 2 t . >>> >t.>

Построение [ править | править код ]

По теореме Гаусса — Ванцеля правильный десятиугольник возможно построить, используя лишь циркуль и линейку.

Иначе его можно построить следующим образом:

1. Построить сначала правильный пятиугольник.
2. Соединить все его вершины с центром описанной окружности прямыми до пересечения с этой же окружностью на противоположной стороне. В этих точках пересечения и находятся остальные пять вершин десятиугольника.
3. Соединить по порядку вершины пятиугольника и пять точек, найденные шагом ранее. Искомый десятиугольник построен.

Видео:Построение девятиугольника циркулем, приближенноеСкачать

Разбиение правильного десятиугольника [ править | править код ]

Гарольдом Коксетером было доказано, что правильный 2 m -угольник можно разбить на m ( m − 1 ) 2 >> ромбов. Для декагона m = 5 , так что он может быть разбит на 10 ромбов.

Видео:Деление окружности на 5 частей с помощью циркуляСкачать

Пространственный десятиугольник [ править | править код ]

Правильные пространственные десятиугольники
#	#	#

Пентаграммная антипризма с перекрёстом

Пространственный десятиугольник — это пространственный многоугольник с десятью рёбрами и вершинами, но не лежащими в одной плоскости. У пространственного зиг-заг десятиугольника вершины чередуются между двумя параллельными плоскостями.

У правильного пространственного десятиугольника все рёбра равны. В трёхмерном пространстве это зиг-заг пространственный декагон, он может быть обнаружен среди рёбер и вершин пентагональной антипризмы, пентаграммной антипризмы, пентаграммной перекрещивающейся антипризмы с той же D_5d [2 + ,10] симметрией порядка 20.

Его также можно найти в некоторых выпуклых многогранниках с икосаэдрической симметрией. Многоугольники по периметру этих проекций (см. ниже) это пространственные десятиугольники.

Ортогональные проекции многогранников
Додекаэдр	Икосаэдр	Икосододекаэдр	Ромботриаконтаэдр

Многоугольники Петри [ править | править код ]

Правильный пространственный десятиугольник — это многоугольник Петри для многих многогранников высших размерностей, как показано на этих ортогональных проекциях на различных плоскостях Коксетера.

Видео:Как нарисовать правильный пятиугольник | Видеоурок MATHANIMATIONСкачать

Построение правильного десятиугольника

Видео:Как начертить пятиугольник вписанный в круг или звездаСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Описание слайда:

Построение правильного
десятиугольника

Геометрия 9 класс
Правильные многоугольники
Авторы презентации: учителя информатики Приволжского района г.Казани -Талызина Л.К. ,Ларина А.У

Описание слайда:

Компьютерное тестирование
Задачи на построение
Построение правильного десятиугольника
Творческое задание на компьютере: «Математические человечки»;
Творческое домашнее задание
Используемая литература

Описание слайда:

Верно ли утверждение: если в многоугольнике все углы равны, то он правильный?
Найти число сторон правильного многоугольника, если его центральный угол равен 200.
Найти углы правильного десятиугольника.
Чему равна сумма внешних углов правильного n –угольника?
Пчелиные соты имеют форму многоугольника, сумма внутренних углов которого равна 7200.Найти число сторон этой соты.
Определить вид многоугольника., если каждая сторона его равна радиусу описанной окружности?
Найти отношение сторон правильного треугольника и шестиугольника, вписанных в окружность.
Вопросы компьютерного тестирования

Описание слайда:

Задачи на построение
Задача о построении циркулем и линейкой правильных многоугольников изучалась еще древнегреческими геометрами, а окончательно была решена лишь в 1801 году великим немецким математиком Карлом Гауссом.

На рисунке изображена лишь небольшая часть правильного многоугольника. Как узнать, сколько у него сторон? Закончить построение многоугольника.

2. Около правильного шестиугольника описана окружность. Предложить три способа нахождения центра этой окружности

Описание слайда:

Построение правильного десятиугольника
Алгоритм построения
1.Провести окружность O радиуса OA.
2.Из точки O1, как из центра, провести окружность, радиуса OO1.
3.Соединить точки A и O1.
4. Точку пересечения отрезка OA1 с окружностью обозначить B
5.AB- будет равен стороне искомого десятиугольника.
6.Из точки A , как из центра, провести окружность радиуса AB
7. Соединить точку пересечения окружности с точкой A
8.Полученный отрезок будет 1 стороной десятиугольника
и т.п.
Задание выполнено на компьютере в среде Free Hand

Описание слайда:

Математические человечки
Игра – шутка
Нарисовать на компьютере в среде Free Hand несколько человечков с помощью математических фигур. Затем подсчитать количество треугольников, квадратов, окружностей. По результатам можно определить какое качество преобладает в человеке: треугольник – ум, окружность – доброта, квадрат – интеллигентность. Затем можно выбрать самого умного, доброго, интеллигентного.

Описание слайда:

Творческое домашнее задание
Сделать паркет из правильных многоугольников

Описание слайда:

Используемая литература
Б. А. Кордемский. «Великие жизни в математике»
Н. Л. Вадченко «Проверьте свои знания»
С. Коваль «От развлечения к знаниям»
А. В. Погорелов «Геометрия. 7-11 классы»
Справочная литература
Дополнительная литература

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

• Сейчас обучается 353 человека из 65 регионов

Курс повышения квалификации

Охрана труда

• Сейчас обучается 103 человека из 46 регионов

Курс профессиональной переподготовки

Охрана труда

• Сейчас обучается 217 человек из 54 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Похожие материалы

Влияние изменения солнечной активностина напряженное состояние и геодинамику земной коры Урала Зубк

Каждый байт под защитой!

УТЁСОВА Е.А. УЧИТЕЛЬ МАТЕМАТИКИ МОУ СОШ№80 г. СОЧИ

Уральский экономический район

Реки города Челябинска Шкерина С.В., учитель географии и краеведения МОУ СОШ № 65 г.Челябинска

Подземные богатства Южного Урала

Инвестиционный стандарт: выполнение требований по информации

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5468677 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В Госдуме обсудят введение обязательных тестов на наркотики в школах

Время чтения: 1 минута

Стартовал региональный этап Всероссийской олимпиады школьников

Время чтения: 2 минуты

Порядка 65% выпускников российских вузов идут работать по специальности

Время чтения: 1 минута

Федеральный перечень учебников будет дополнен новыми учебниками

Время чтения: 3 минуты

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать

Геометрия

А Вы уже инвестируете?
Слышали про акцию в подарок?

Зарегистрируйся по этой ссылке
и получи акцию до 100.000 руб

План урока:

Видео:Построение 12 угольника циркулемСкачать

Понятие правильного многоугольника

У выпуклого многоугольника могут быть одинаковы одновременно и все стороны, и все углы. В таком случае он именуется правильным многоугольником.

Нам уже известны некоторые правильные многоуг-ки. Например, правильным является равносторонний треугольник. У него все стороны одинаковы по его определению, а все углы составляют по 60°. Поэтому иногда его так и называют – правильный треугольник. Среди четырехугольников правильной фигурой является квадрат, у которого также по определению одинаковы стороны, а углы составляют уже по 90°.

Заметим, что бывают фигуры, у которых одинаковы все стороны, а углы различны. Примером такой фигуры является ромб. Возможна и обратная ситуация – все углы у фигуры одинаковы, но стороны отличаются своей длиной. Таковым является прямоугольник. Важно понимать, такие фигуры (в частности, ромб и прямоугольник) НЕ являются правильными.

Для любого заданного числа n, начиная от n = 3, можно построить правильный n-угольник. На рисунке ниже показано несколько примеров таких n-угольников:

Существует зависимость, которая позволяет определить величину угла правильного многоугольника. Мы уже знаем, что в любом выпуклом n-угольнике сумма углов равна величине 180°(n– 2). Обозначим угол правильного многоуг-ка буквой α. Так как у n-угольника ровно n углов, и все они одинаковы, мы можем записать равенство:

Легко проверить, что эта формула верна для равностороннего треуг-ка и квадрата и позволяет правильно определить углы в этих фигурах. Для треугольника n = 3, поэтому мы получаем 60°:

Задание. Какова величина углов в правильном пятиугольнике, шестиугольнике, восьмиугольнике, пятидесятиугольнике?

Решение. Надо просто подставить в формулу число сторон правильного многоугольник. Сначала считаем для пятиугольника:

Задание. Сколько сторон должно быть у правильного многоуг-ка, чтобы каждый угол в нем был равен 179°?

Решение. В формулу

Задание. Может ли существовать правильный многоуг-к, угол которого равен 145°?

Решение. Предположим, что он существует. Тогда по аналогии с предыдущей задачей найдем количество его сторон:

Получили не целое, а дробное количество сторон. Естественно, что это невозможно, а потому такой многоуг-к существовать не может.

Видео:Как нарисовать пятиконечную ЗВЕЗДУ с помощью циркуляСкачать

Описанная и вписанная окружности правильного многоугольника

Докажем важную теорему о правильном многоуг-ке.

Для доказательства обозначим вершины произвольного правильного n-угольника буквами А₁, А₂, А₃…А_n. Далее проведем биссектрисы углов ∠А₁ и ∠А₂. Они пересекутся в некоторой точке О. Соединим О с другими вершинами многоуг-ка отрезками ОА₃, ОА₄ и т. д.

∠А₁ и ∠А₂ одинаковы по определению правильного многоуг-ка:

Из этого факта вытекает два равенства:

Получается, что ОА₃ – это также биссектриса ∠А₃. Тогда, повторив все предыдущие рассуждения, мы можем доказать равенство, аналогичное (1):

Это равенство означает, что точка О равноудалена от вершин многоуг-ка. Значит, можно построить окружность с центром в О, на которой будут лежать все вершины многоуг-ка:

Естественно, существует только одна такая описанная окружность, ведь через любые три точки, в частности, через А₁, А₂ и А₃, можно провести только одну окружность, ч. т. д.

Продолжим рассматривать выполненное нами построение с описанной окружностью. Ясно, что ∆ОА₁А₂, ∆ОА₂А₃, ∆ОА₃А₄, …, равны, ведь у них одинаковы по 3 стороны. Опустим из О высоты ОН₁, ОН₂, ОН₃… на стороны многоуг-ка.

Так как высоты проведены в равных треуг-ках, то и сами они равны:

Теперь проведем окружность, центр которой находится в О, а радиус – это отрезок ОН₁. Он должен будет пройти и через точки Н₂, Н₃, … Н_n. Причем отрезки ОН₁, ОН₂, ОН₃ окажутся радиусами. Так как они перпендикулярны сторонам многоуг-ка, то эти самые стороны будут касательными к окружности (по признаку касательной). Стало быть, эта окружность является вписанной:

Ясно, что такая окружность будет единственной вписанной. Если бы существовала вторая вписанная окружность, то ее центр был бы равноудален от сторон многоуг-ка, а потому лежал бы в точке пересечения биссектрис углов ∠А₁, ∠А₂, ∠А₃, то есть в точке О. Так как расстояние от О до А₁А₂ – это отрезок ОН₁, то именно такой радиус был бы у второй окружности. Получается, что вторая окружность полностью совпала бы с первой, так как их центр находился бы в одной точке, и радиусы были одинаковы.

Примечание. Точка, которая центром и вписанной, и описанной окружности, именуется центром правильного многоуг-ка.

Ещё раз вернемся к приведенному доказательству и заметим, что высоты ОН₁, ОН₂, ОН₃,… проведены в равнобедренных треуг-ках∆ОА₁А₂, ∆ОА₂А₃, ∆ОА₃А₄,… Следовательно, эти высоты являются ещё и медианами, то есть точки Н₁, Н₂, Н₃,… – это середины сторон многоуг-ка.

Задание. Могут ли две биссектрисы, проведенные в правильном многоуг-ке, быть параллельными друг другу?

Решение. Центр правильного многоуг-ка находится в точке пересечения всех его биссектрис. То есть любые две биссектрисы будут иметь хотя бы одну общую точку. Параллельные же прямые общих точек не имеют. Получается, что биссектрисы не могут быть параллельными.

Примечание. Аналогичное утверждение можно доказать и для серединных перпендикуляров, проведенных к сторонам правильного многоуг-ка.

Видео:Геометрия - Построение десятиугольникаСкачать

Формулы для правильного многоугольника

Правильный многоуг-к, как и любая другая плоская фигура, имеет площадь (она обозначается буквой S) и периметр (обозначается как Р). Длина стороны многоуг-ка традиционно обозначается буквой a_n, где n– число сторон у многоуг-ка. Например a₄– это сторона квадрата, a₆– сторона шестиугольника. Наконец, мы выяснили, что для каждого правильного многоуг-ка можно построить описанную и вписанную окружность. Радиус описанной окружности обозначается большой буквой R, а вписанной – маленькой буквой r.

Оказывается, все эти величины взаимосвязаны друг с другом. Ранее мы уже получили формулу

для многоуг-ка, в который вписана окружность. Подходит она и для правильного многоуг-ка.

Для вывода остальных формул правильного многоугольника построим n-угольники соединим две его вершины с центром:

Теперь у нас есть формула, связывающая друг с другом Rи r. Наконец, прямо из определения периметра следует ещё одна формула:

С их помощью, зная только один из параметров правильного n-угольника, легко найти и все остальные параметры (если известно и число n).

Задание. Докажите, что сторона правильного шестиугольника равна радиусу описанной около него окружности.

Решение. Запишем следующую формулу:

Это равенство как раз и надо было доказать в этом задании.

Задание. Около окружности описан квадрат. В свою очередь и около квадрата описана окружность радиусом 4. Найдите длину стороны квадрата и радиус вписанной окружности.

Решение. Запишем формулу:

Задание. Вычислите площадь правильного многоугольника с шестью углами, длина стороны которого составляет единицу.

Найдем периметр шестиугольника:

Задание. Около правильного треугольника описана окружность. В ту же окружность вписан и квадрат. Какова длина стороны этого квадрата, если периметр треугольника составляет 18 см?

Решение. Зная периметр треуг-ка, легко найдем и его сторону:

Далее вычисляется радиус описанной около треугольника окружности:

Задание. Необходимо изготовить болт с шестигранной головкой, причем размер под ключ (так называется расстояние между двумя параллельными гранями головки болта) должен составлять 17 мм. Из прутка какого диаметра может быть изготовлен такой болт, если диаметр прутков измеряется целым числом?

Решение. Здесь надо найти диаметр окружности, описанной около шестиугольника. Ранее мы уже доказывали, что у шестиугольника длина этого радиуса совпадает с длиной его стороны:

Осталось найти сторону шестиугольника. Для этого соединим две его вершины (обозначим их А и С) так, как это показано на рисунке:

Отрезок АС как раз и будет расстоянием между двумя параллельными гранями, что легко доказать. Каждый угол шестиугольника будет составлять 120°:

В частности ∠АВС = 120°. Так как АВ = ВС, то ∆АВС – равнобедренный, и углы при его основании одинаковы:

Аналогично можно показать, что и ∠ACD – прямой. Таким образом, АС перпендикулярен сторонам AF и CD, а значит является расстоянием между ними, и по условию равно 17 мм:

∆АВС – равнобедренный. Опустим в нем высоту НВ, которая одновременно будет и медианой. Тогда АН окажется вдвое короче АС:

AH = AC/2 = 17/2 = 8,5 мм

Теперь сторону АВ можно найти из ∆АВН, являющегося прямоугольным:

Здесь мы округлили ответ до ближайшего большего целого числа, так как по условию можно использовать лишь пруток с целым диаметром.

Видео:1 2 3 деление окружности на 7 равных частейСкачать

Построение правильных многоугольников

При использовании транспортира или иного прибора, позволяющего откладывать заранее заданные углы, построение правильного многоуг-ка проблем не вызывает. Например, пусть надо построить пятиугольник со стороной, равной 5 см. Сначала по известной формуле вычисляем величину его угла:

Однако напомним, что в геометрии большой интерес вызывают задачи, связанные с построением с помощью всего двух инструментов – циркуля и линейки, то есть без использования транспортира. В таком случае построение многоугольников правильной формы становится значительно более сложной задачей. Если речь идет не о таких простых фигурах, как квадрат и равносторонний треугольник, то при построении обычно приходится использовать описанную окружность.

Сначала рассмотрим построение правильного шестиугольника по заранее заданной стороне. Ранее мы уже узнали, что его сторона имеет такую же длину, как и радиус описанной окружности:

На основе этого факта предложен следующий метод построения шестиугольника. Сначала строится описанная окружность, причем в качестве ее радиуса берется заданная сторона а₆. Далее на окружности отмечается произвольная точка А, которая будет первой вершиной шестиугольника. Из нее проводится ещё одна окружность радиусом а₆. Точки, где она пересечет описанную окружность (В и F), будут двумя другими вершинами шестиугольника. Наконец, и из точек B и F проводим ещё две окружности, которые пересекутся с исходной окружностью в точках С и F. Наконец, из С (можно и из F)провести последнюю окружность и получить точку D. Осталось лишь соединить все точки на окружности (А, В, С, D, Еи F):

Данное построение довольно просто. Однако для пятиугольника построение несколько более сложное, а для семиугольника и девятиугольника вообще невозможно осуществить точное построение. Этот факт был доказан только в 1836 г. Пьером Ванцелем.

Если удалось возможно построить правильный n-угольник, вписанный в окружность, то несложно на его основе построить многоуг-к, у которого будет в два раза больше сторон (его можно назвать 2n-угольником) и который будет вписан в ту же окружность. Рассмотрим это построение на примере квадрата и восьмиугольника.

Изначально дан квадрат, вписанный в окружность. Надо построить восьмиугольник, вписанный в ту же окружность. Обозначим любые две вершины квадрата буквами А и В. Для начала нам надо разбить дугу ⋃АВ на две равные дуги. Для этого мы проводим из А и В окружности радиусом АВ. Они пересекутся в некоторых точках С и D. Соединяем их отрезком, который в свою очередь пересечется с исходной окружностью в точке Е.

Е – это середина дуги ⋃АВ. Точки А, В и Е как раз являются тремя первыми точками восьмиугольника. Для получения остальных точек необходимо из вершин квадрата строить окружности радиусом АЕ. Точки, где эти окружности пересекутся с исходной окружностью, и будут вершинами восьмиугольника. Также его вершинами являются вершины самого квадрата:

Аналогичным образом можно из шестиугольника получить 12-угольник, из восьмиугольника – 16-угольник, из 16-угольника – 32-угольник. То есть можно удвоить число сторон многоуг-ка.

Древние греки умели строить правильные многоуг-ки с 3, 4, 5, 6 и 15 сторонами, а также умели на их основе строить многоуг-ки с вдвое большим числом сторон. Лишь в 1796 г. Карл Гаусс смог построить 17-угольник. Также удалось найти способ построения 257-угольника и 65537-угольника, причем описание построения 65537-угольника занимает более 200 страниц.

В этом уроке мы узнали о правильных многоуг-ках и их свойствах. Особенно важно то, что для каждого такого многоуг-ка можно построить описанную и вписанную окружность, причем их центры совпадают. Это позволяет использовать правильные многоуг-ки для более глубокого исследования свойств окружности.

📽️ Видео

4K Как построить правильный пятиугольник, how to draw a regular pentagonСкачать

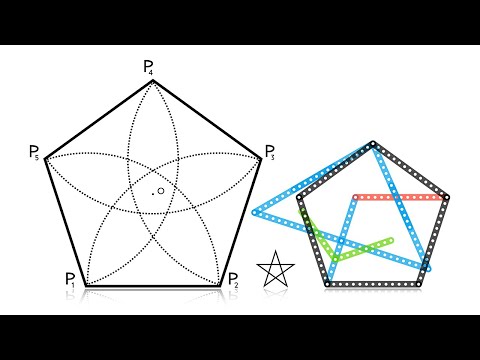
4K Как построить десятиугольник, regular decagon constructionСкачать