Как отмечать точки на окружности тригонометрия (5 видео)

Числовая окружность

В этой статье мы очень подробно разберем определение числовой окружности, узнаем её главное свойство и расставим числа 1,2,3 и т.д. Про то, как отмечать другие числа на окружности (например, (frac, frac, frac, 10π, -frac)) разбирается в этой статье .

Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют действительным числам , расставленным по следующим правилам:

1) Начало отсчета находится в крайней правой точке окружности;

2) Против часовой стрелки — положительное направление; по часовой – отрицательное;

3) Если в положительном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (t);

4) Если в отрицательном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (–t).

Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.

Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.

Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен (1). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках (1) и (-1).

Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).

Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы (l=2πR) мы получим:

Содержание

Длина числовой окружности равна (2π) или примерно (6,28).
Какие точки соответствуют числам (1), (2) и т.д?
Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.
Главное свойство числовой окружности
Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.
Все значения одной точки на числовой окружности можно записать с помощью формулы:
Тригонометрический круг: вся тригонометрия на одном рисунке
А теперь подробно о тригонометрическом круге:
Тригонометрические уравнения
🎬 Видео

Длина числовой окружности равна (2π) или примерно (6,28).

А что значит «…точки которой соответствуют действительным числам»?
Как говорили выше, на числовой окружности для любого действительного числа обязательно найдется его «место» — точка, которая соответствует этому числу.

Зачем определять на числовой окружности начало отсчета и направления?
Главная цель числовой окружности — каждому числу однозначно определить свою точку. Но как можно определить, где поставить точку, если неизвестно откуда считать и куда двигаться?

Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте (1) на оси (x) и (0) на окружности – это точки на разных объектах.

Видео:Как искать точки на тригонометрической окружности.Скачать

Какие точки соответствуют числам (1), (2) и т.д?

Помните, мы приняли, что у числовой окружности радиус равен (1)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.

Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.

Чтобы отметить на окружности точку соответствующую числу (2), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы (3) – расстояние равное трем радиусам и т.д.

При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.

2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.

К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: (2π). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа (π) : ( frac),(-frac),(frac), (2π). Поэтому при работе с окружностью чаще используют числа с (π). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье ).

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Главное свойство числовой окружности

Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.

Такая вот математическая полигамия.

И следствие из этого правила:

Все значения одной точки на числовой окружности можно записать с помощью формулы:

Если хотите узнать логику этой формулы, и зачем она нужна, посмотрите это видео .

В данной статье мы рассмотрели только теорию о числовой окружности, о том как расставляются точки на числовой и окружности и принципе, как с ней работать вы можете прочитать здесь .

Что надо запомнить про числовую окружность:

Видео:Тригонометрическая окружность. Как выучить?Скачать

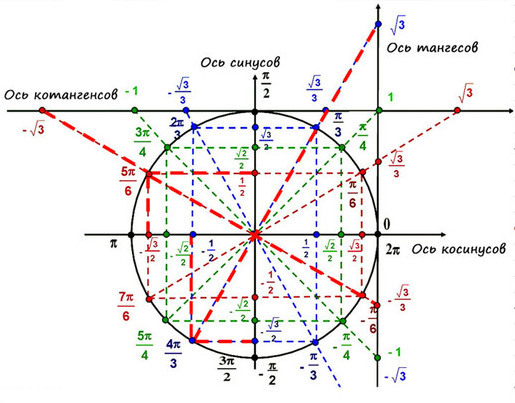
Тригонометрический круг: вся тригонометрия на одном рисунке

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.

Вот что мы видим на этом рисунке:

Перевод градусов в радианы и наоборот. Полный круг содержит градусов, или радиан.

Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси , а значение синуса — на оси .

И синус, и косинус принимают значения от до .

Значение тангенса угла тоже легко найти — поделив на . А чтобы найти котангенс — наоборот, косинус делим на синус.

Знаки синуса, косинуса, тангенса и котангенса.

Синус — функция нечётная, косинус — чётная.

Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен .

Видео:Тригонометрия. Часть 1. Как отмечать точки на единичной окружности.Скачать

А теперь подробно о тригонометрическом круге:

Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.

Мы отсчитываем углы от положительного направления оси против часовой стрелки.

Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Всё это легко увидеть на нашем рисунке.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :

Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).

Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.

Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.

Легко заметить, что

Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:

где — целое число. То же самое можно записать в радианах:

Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,

Видео:Изобразить на единичной окружности точку.Скачать

Тригонометрические уравнения

Решение простейших тригонометрических уравнений

Градусы и радианы

Знакомство с тригонометрической окружностью

Повороты на тригонометрической окружности

Как много боли связано со словом тригонометрия. Эта тема появляется в 9 классе и уже никуда не исчезает. Тяжело приходится тем, кто чего-то не понял сразу. Попробуем это исправить, чтобы осветить ваше лицо улыбкой при слове тригонометрия или хотя бы добиться «poker face».

Начнем с того, что как длину можно выразить в метрах или милях, так и угол можно выразить в радианах или градусах .

1 радиан = 180/π ≈ 57,3 градусов

Но проще запомнить целые числа: 3,14 радиан = 180 градусов. Это все одно и то же значение числа π.

Вспомним, что если нас просят развернуться, то нам нужно повернуться на 180 градусов, а теперь можно так же сказать: Повернись на π!

О графиках синуса, косинуса и тангеса поговорим в другой статье.

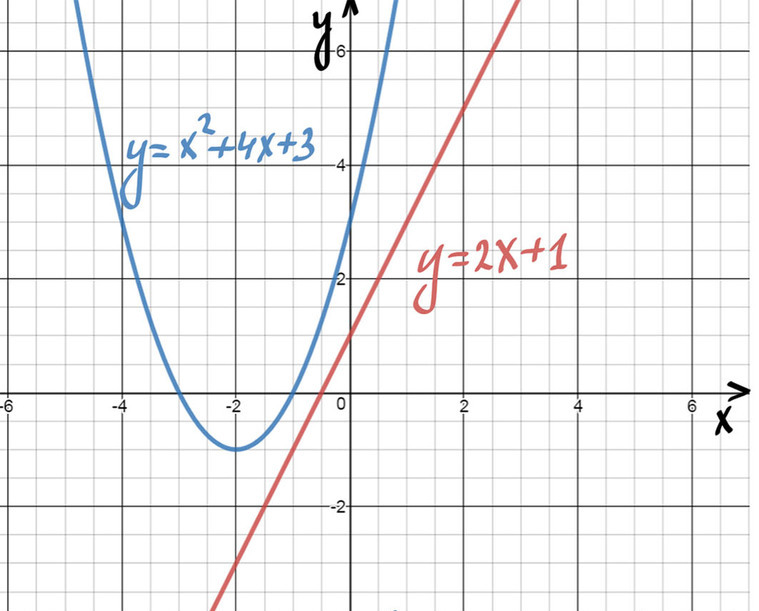
А сейчас начем с декартовой (прямоугольной) системы координат.

Раньше она помогала строить графики, а теперь поможет с синусом и косинусом.

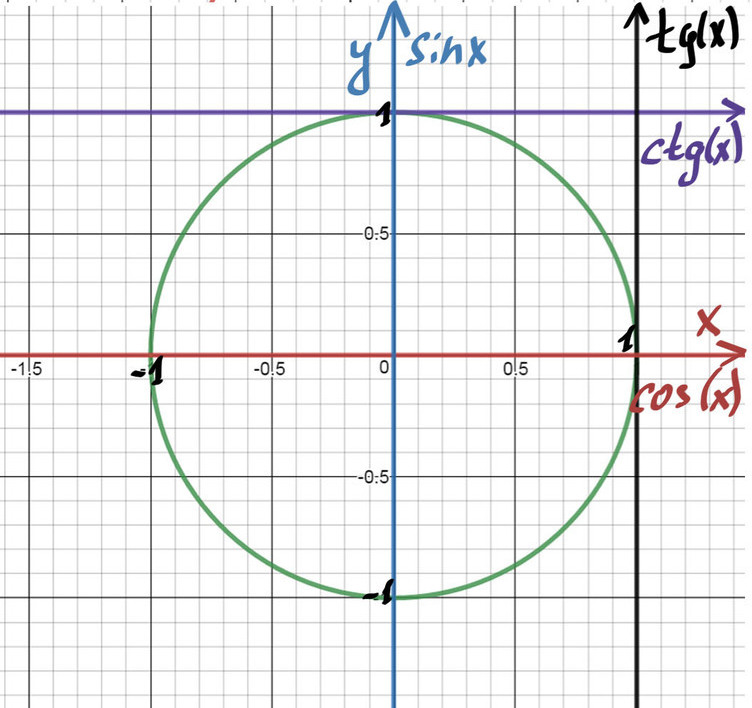
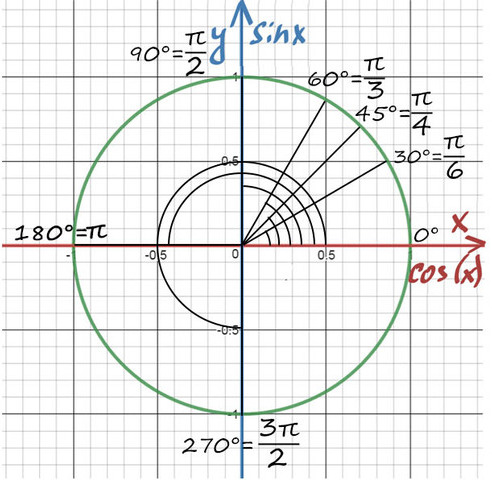
На пересечении оси Х и оси Y построим единичную (радиус равен 1) окружность:

Тогда ось косинусов будет совпадать с х, ось синусов с y. Оси тангенсов и котангенсов также показаны на рисунке.

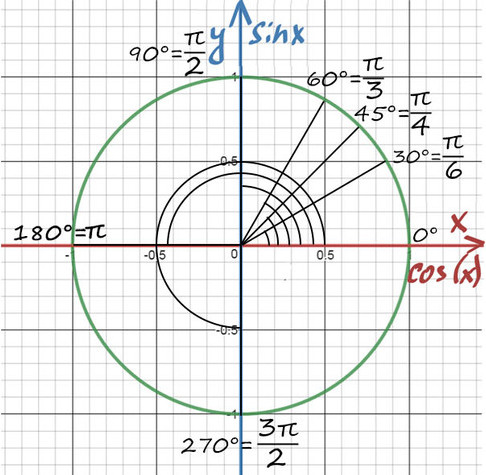
А теперь отметим основные значения градусов и радиан на окружности.

Давай договоримся с тобой, как взрослые люди: на окружности мы будем отмечать угол в радианах, то есть через Пи.

Достаточно запомнить, что π = 180° (тогда π/6 = 180/6 = 30°; π/3 = 180/3 = 60°; π/4 = 180/4 = 45°).

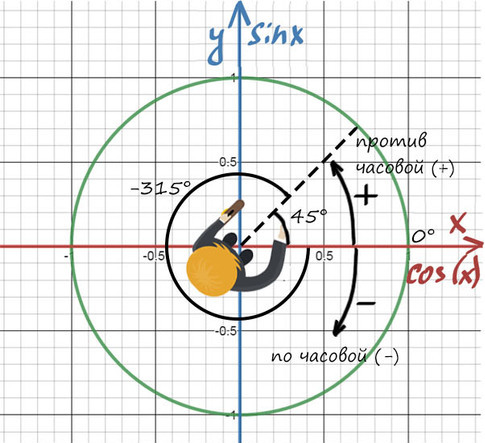
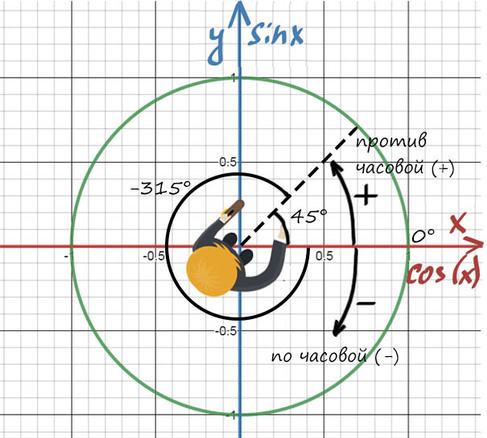
А теперь давай покрутимся на окружности! За начало отчета принято брать крайнюю правую точку окружности (где 0°):

От нее задаем дальнейший поворот. Вращаться можем как в положительную сторону (против часовой), так и в отрицательную сторону (по часовой стрелке).

Повернуться на 45° можно двумя спобами: через левое плечо на 45° в (+) сторону, либо через правое плечо на 315° в (-).

Главное — направление, куда мы будем смотреть, а не угол!

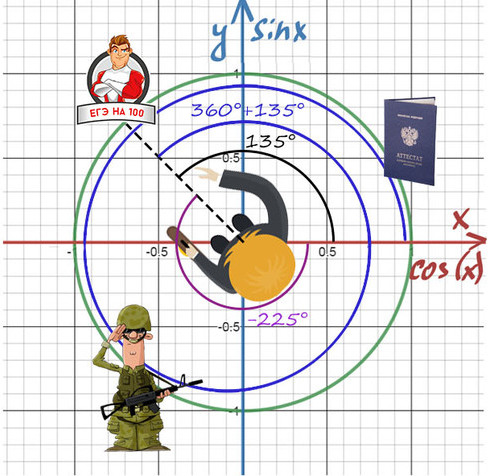
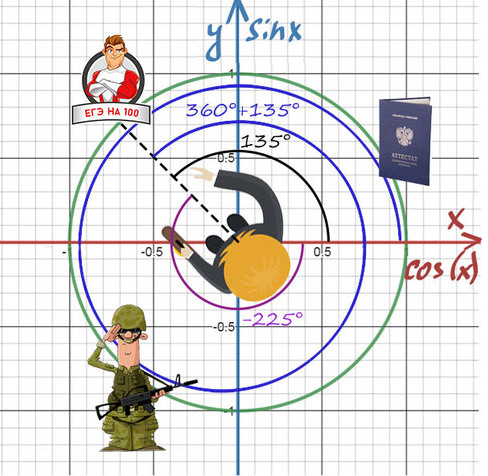
Нужно направить пунктир на 100 баллов, а сколько оборотов и в какую сторону вокруг себя мы сделаем — без разницы!

Получить 100 баллов можно поворотом на 135° или 360°+135°, или -225°, или -225°-360°.

А теперь у тебя есть два пути:

Выучить всю окружность (тригонометр). Неплохой вариант, если с памятью у тебя все отлично, и ничего не вылетит из головы в ответственный момент:

А можно запомнить несколько табличных углов и соответствующие им значения, а потом использовать их.

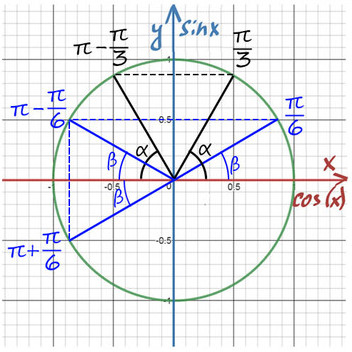
Находите равные углы (вертикальные, соответственные) на тригонометрической окружности. Попасть в любую точку можно с помощью суммы или разности двух табличных значений.

Сразу попробуем разобрать на примере:

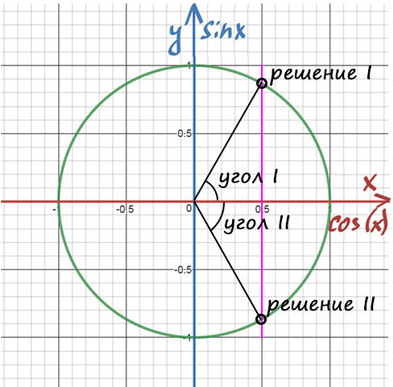
1) Помним, что ось cos(x) — это горизонтальная ось. На ней отмечаем значение ½ и проводим перпендикулярную (фиолетовую) прямую до пересечений с окружностью.

2) Получили две точки пересечения с окружностью, значение этих углов и будет решением уравнения.

Дело за малым — найти эти углы.

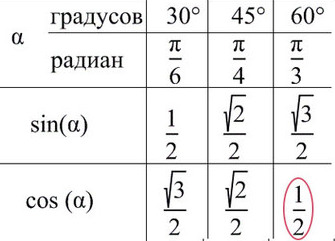
Лучше обойтись «малой кровью» и выучить значение синуса и косинуса для углов от 30° до 60°.

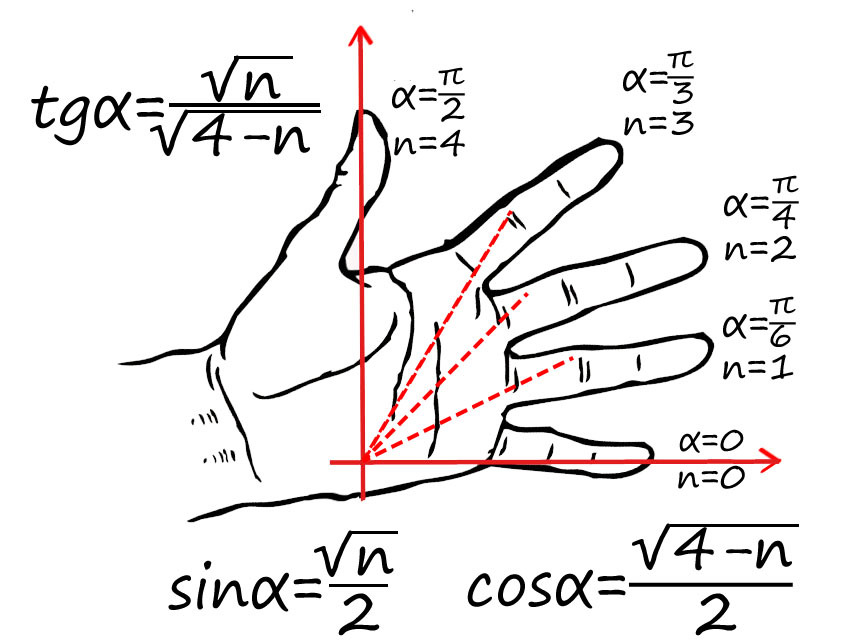
Или запомнить такой прием:

Пронумеруй пальцы от 0 до 4 от мизинца до большого. Угол задается между мизинцем и любым другим пальцем (от 0 до 90).

Например, требуется найти sin(π/2) : π/2 — это большой палец, n = 4 подставляем в формулу для синуса: sin(π/2) = √4/2 = 1 => sin(π/2) = 1.

cos(π/4) — ? π/4 соответсвует среднему пальцу (n = 2) => cos(π/4) = √2/2.

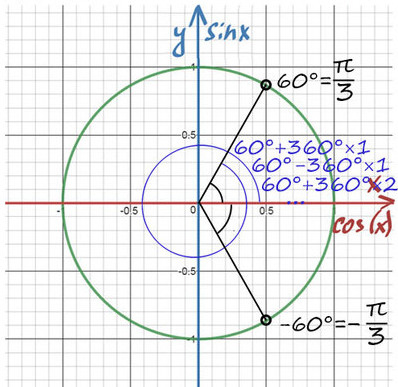
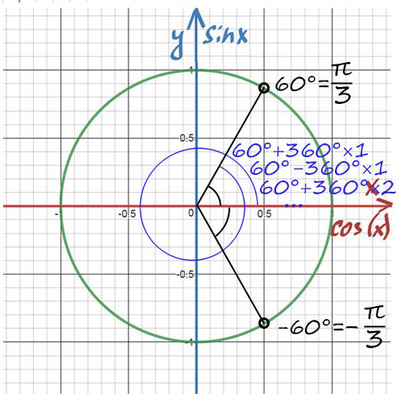
При значении cos(x) = ½ из таблицы или с помощью мнемонического правила находим x = 60° (первая точка x = +π/3 из-за того, что поворот происходил против часовой стерелки (+), угол показан черной дугой).

Вторая же точка соответствует точно такому же углу, только поворот будет по часовой стрелке (−). x = −π/3 (угол показан нижней черной дугой).

И последнее, прежде чем тебе, наконец, откроются тайные знания тригонометрии:

Когда требуется попасть в «100 баллов», мы можем в них попасть с помощью поворота на . =-225°=135°=495°=.

То же самое и здесь! Разные углы могут отражать одно и то же направление.

Абсолютно точно можно сказать, что нужно повернуться на требуемый угол, а дальше можно поворачиваться на 360° = 2π (синим цветом) сколько угодно раз и в любом направлении.

Таким образом, попасть в первое направление 60° можно: . 60°-360°, 60°, 60°+360°.

И как записать остальные углы, не записывать же бесконечное количество точек? (Хотел бы я на это посмотреть☻)

Поэтому правильно записать ответ: x = 60 + 360n, где n — целое число (n∈Ζ) (поворачиваемся на 60 градусов, а после кружимся сколько угодно раз, главное, чтобы направление осталось тем же). Аналогично x = −60 + 360n.

Но мы же договорились, что на окружности все записывают через π, поэтому cos(x) = ½ при x = π/3 + 2πn, n∈Ζ и x = −π/3 + 2πk, k∈Ζ.

Ответ: x = π/3 + 2πn, x= − π/3 + 2πk, (n, k) ∈Ζ.

Пример №2. 2sinx = √2

Первое, что следует сделать, это перенести 2-ку вправо => sinx=√2/2

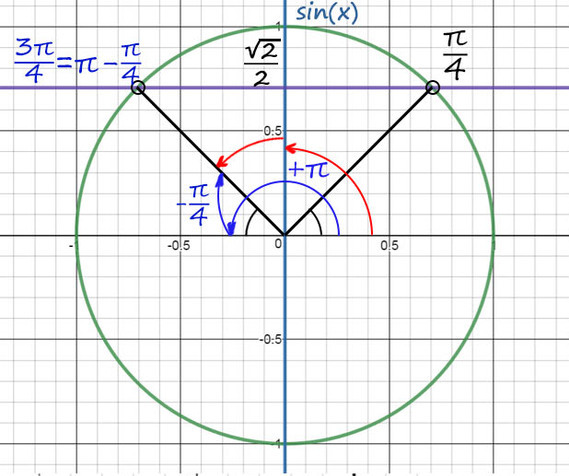
1) sin(x) совпадает с осью Y. На оси sin(x) отмечаем √2/2 и проводим ⊥ фиолетовую прямую до пересечений с окружностью.

2) Из таблицы sinx = √2/2 при х = π/4, а вторую точку будем искать с помощью поворота до π, а затем нужно вернуться обратно на π/4.

Поэтому вторая точка будет x = π − π/4 = 3π/4, в нее также можно попасть и с помощью красных стрелочек или как-то по-другому.

И еще не забудем добавить +2πn, n∈Ζ.

Ответ: 3π/4 + 2πn и π/4 + 2πk, k и n − любые целые числа.

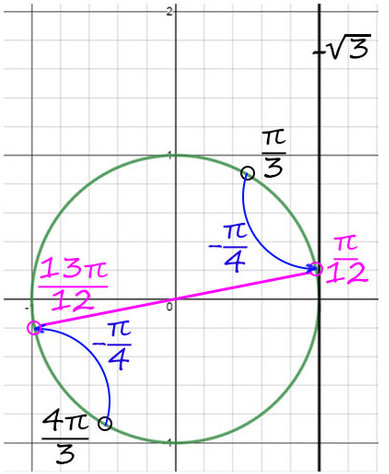
Пример №3. tg(x + π/4) = √3

Вроде все верно, тангенс равняется числу, но смущает π/4 в тангенсе. Тогда сделаем замену: y = x + π/4.

tg(y) = √3 выглядит уже не так страшно. Вспомним, где ось тангенсов.

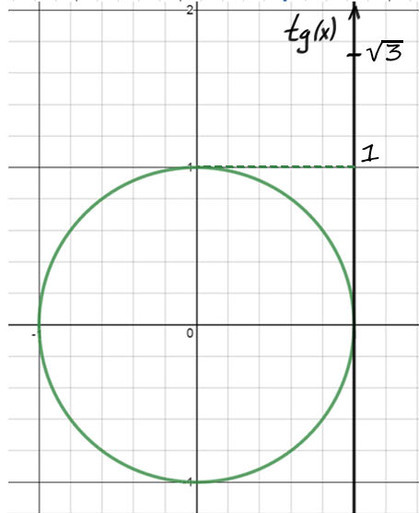
1) А теперь на оси тангенсов отметим значение √3, это выше чем 1.

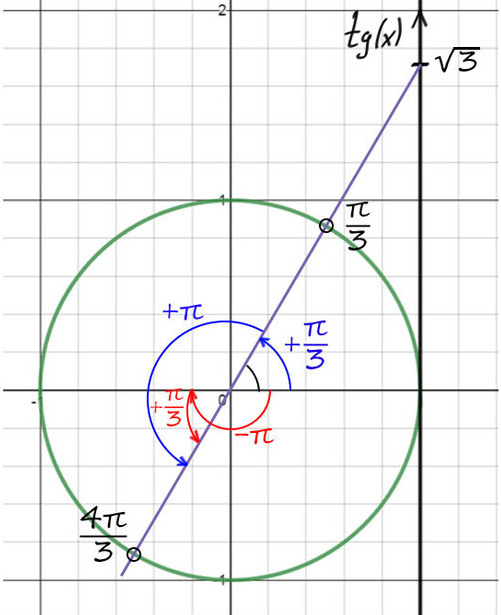
2) Проведем фиолетовую прямую через значение √3 и начало координат. Опять на пересечении с окружностью получается 2 точки.

По мнемоническому правилу при тангенсе √3 первое значение — это π/3.

3) Чтобы попасть во вторую точку, можно к первой точке (π/3) прибавить π => y = π/3 + π = 4π/3.

4) Но мы нашли только y , вернемся к х. y = π/3 + 2πn и y = x + π/4, тогда x + π/4 = π/3 + 2πn => x = π/12 + 2πn, n∈Ζ.

Второй корень: y = 4π/3 + 2πk и y = x + π/4, тогда x + π/4 = 4π/3 + 2πk => x = 13π/12 + 2πk, k∈Ζ.

Теперь корни на окружности будут здесь:

Ответ: π/12 + 2πn и 13π/12 + 2πk, k и n — любые целые числа.

Конечно, эти два ответа можно объединить в один. От 0 поворот на π/12, а дальше каждый корень будет повторяться через каждый π (180°).

Ответ можно записать и так: π/12 + πn, n∈Ζ.

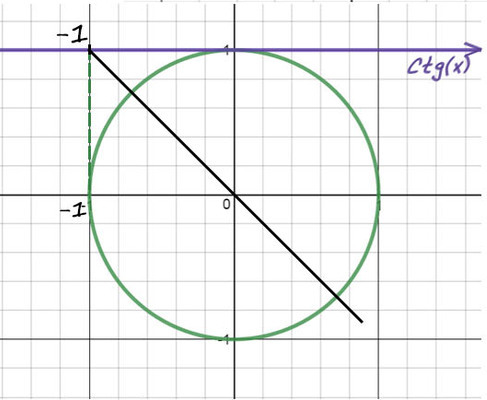
Пример №4: −10ctg(x) = 10

Перенесем (−10) в другую часть: ctg(x) = −1. Отметим значение -1 на оси котангенсов.

1) Проведем прямую через эту точку и начало координат.

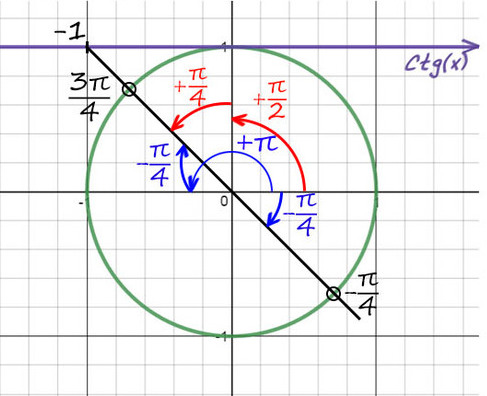
2) Придется опять вспомнить, когда деление косинуса на синус даст еденицу (это получается при π/4). Но здесь −1, поэтому одна точка будет −π/4. А вторую найдем поворотом до π, а потом назад на π/4 (π − π/4).

Можно это сделать по-другому (красным цветом), но мой вам совет: всегда отсчитывайте от целых значений пи (π, 2π, 3π. ) так намного меньше шансов запутаться.

Не забываем добавить к каждой точке 2πk.

Ответ: 3π/4 + 2πn и −π/4 + 2πk, k и n — любые целые числа.

Алгоритм решения тригонометрических уравнений (на примере cos(x) = − √ 3/2) :

Отмечаем значение (−√3/2) на оси тригонометрической функции (косинусов, это ось Х).
Проводим перпендикулярную прямую оси (косинусов) до пересечений с окружностью.
Точки пересечения с окружностью и будут являться корнями уравнения.
Значение одной точки (без разницы, как в нее попадете) +2πk.

Азов достаточно, прежде чем идти дальше закрепите полученные знания.