Многоугольник вписан в окружность если все его вершины лежат

Окружность описанная около многоугольника — это окружность, на которой лежат все вершины многоугольника. Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности. На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.

Теорема

Доказательство

Дано: произвольный АВС.

Доказать: около АВС можно описать окружность.

Доказательство:

1. Проведем серединные перпендикуляры к сторонам АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).

Точка О равноудалена от вершин АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около АВС. Теорема доказана.

Замечание 1

Доказательство

Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.

Замечание 2

Доказательство

Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

Доказательство

Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).

Углы В и D — вписанные, тогда по теореме о вписанном угле: В = АDС, D = АВС, откуда следует В + D = АDС + АВС = (АDС + АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 360 0 , т.е. АDС + АВС = 360 0 , тогда В + D = 360 0 = 180 0 . Что и требовалось доказать.

Верно и обратное утверждение:

Доказательство

Дано: четырехугольник АВСD, BАD + BСD = 180 0 .

Доказать: около АВСD можно описать окружность.

Доказательство:

Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.

Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.

Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).

ВСD — внешний угол СFD, следовательно, BСD = ВFD + FDE. (1)

Углы ВFD и FDE — вписанные. По теореме о вписанном угле ВFD = ВАD и FDE = ЕF, тогда, подставляя данные равенства в (1), получим: BСD = ВАD + ЕF = (ВАD + ЕF), следовательно, ВСDВАD.

BАD — вписанный, тогда по теореме о вписанном угле BАD = ВЕD, тогда BАD + BСD(ВЕD + ВАD).

Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е. ВЕD + ВАD = 360 0 , тогда BАD + BСD360 0 = 180 0 .

Итак, мы получили, что BАD + BСD180 0 . Но это противоречит условию BАD + BСD =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.

Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).

По теореме о сумме углов треугольника в ВСF: С + В + F = 180 0 , откуда С = 180 0 — ( В + F). (2)

В — вписанный, тогда по теореме о вписанном угле В = ЕF. (3)

F и ВFD — смежные, поэтому F + ВFD = 180 0 , откуда F = 180 0 — ВFD = 180 0 — ВАD. (4)

Подставим (3) и (4) в (2), получим:

С = 180 0 — (ЕF + 180 0 — ВАD) = 180 0 — ЕF — 180 0 + ВАD = (ВАD — ЕF), следовательно, СВАD.

А — вписанный, тогда по теореме о вписанном угле А = ВЕD, тогда А + С(ВЕD + ВАD). Но это противоречит условию А + С =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.

Примечание:

Окружность всегда можно описать:

Поделись с друзьями в социальных сетях:

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Многоугольник. Свойства четырехугольников вписанных в окружность.

Если все вершины какого-нибудь многоугольника (ABCDE) лежат на окружности, то говорят, что этот многоугольник вписан в окружность, или что окружность описана около него.

Теорема.

В выпуклом вписанном четырехугольнике сумма противоположных углов равна двум прямым углам (2d).

Обратная теорема:

Если в выпуклом четырехугольнике сумма противоположных углов равна двум прямым углам (2d), то около него можно описать окружность.

Пусть ABCD — вписанный выпуклый четырехугольник. Необходимо обосновать, что:

Углы B и D, как вписанные будут равны: первый — половиной дуги ADС, второй — половиной дуги ABС. Следовательно, B + D равняется полусумме дуг ADС и ABС, т.е. половиной окружности. Значит, B + D = 2d. Подобно этому убедимся, что A + С= 2d .

Необходимо обосновать, что около такого четырехугольника можно описать окружность. Через какие-нибудь три его вершины, например, A, B, С прочертим окружность (что всегда можно сделать).

Четвертая вершина D должна располагаться на этой окружности, потому что в противном случае угол D лежал бы своей вершиной или внутри круга, или вне его, и тогда этот угол не измерялся бы половиной дуги ABС, поэтому сумма B + D не измерялась бы полусуммой дуг ADС и ABС, т.е. сумма B + D не равнялась бы 2d, что противоречит условию.

Следствия.

1. Из всех параллелограммов только около прямоугольника можно описать окружность.

2. Около трапеции можно описать окружность только тогда, когда она равнобедренная.

Видео:Геометрия 8 класс (Урок№33 - Описанная окружность.)Скачать

Многоугольник вписан в окружность если его вершины лежат

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Вписанные и описанные многоугольники

Вписанным в круг многоугольником называется такой многоугольник, вершины которого лежат на окружности. Описанным около круга многоугольником называется такой многоугольник, стороны которого касаются окружности.

Описанной около многоугольника окружностью называется окружность, проходящая через его вершины. Вписанной в многоугольник окружностью называется окружность, касающаяся его сторон.

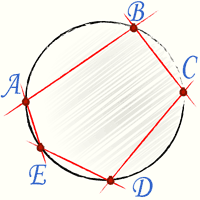Вписанный многоугольник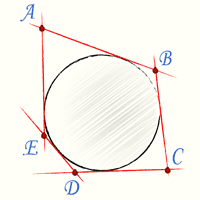

Описанный многоугольник

Если многоугольник взят произвольно, то в него нельзя вписать и около него нельзя описать окружность. Только многоугольники соответствующие некоторым правилам можно описать окружностью или вписать в них окружность.

Видео:9 класс. Правильный многоугольник, вписанный в окружность и описанный около окружностиСкачать

Правила для многоугольников которые можно вписать в окружность и описать окружность вокруг них

Для треугольника всегда возможны и вписанная окружность и описанная окружность.

Для четырехугольника окружность можно вписать только в том случае, если суммы его противоположных сторон одинаковы. Из всех параллелограммов только в ромб и квадрат можно вписать окружность. Ее центр лежит на пересечении диагоналей.

Вокруг четырехугольника окружность можно описать только если сумма противоположных углов равна 180°. Из всех параллелограммов только около прямоугольника и квадрата можно описать окружность. Ее центр лежит на пересечении диагоналей.

Вокруг трапеции возможно описать окружность или в трапецию можно вписать окружность если трапеция равнобокая.

Видео:9 класс. Правильный многоугольник, вписанный в окружность и описанный около окружности. Мерзляк А.Г.Скачать

Многоугольник. Свойства четырехугольников вписанных в окружность.

Если все вершины какого-нибудь многоугольника (ABCDE) лежат на окружности, то говорят, что этот многоугольник вписан в окружность, или что окружность описана около него.

Теорема.

В выпуклом вписанном четырехугольнике сумма противоположных углов равна двум прямым углам (2d).

Обратная теорема:

Если в выпуклом четырехугольнике сумма противоположных углов равна двум прямым углам (2d), то около него можно описать окружность.

Пусть ABCD — вписанный выпуклый четырехугольник. Необходимо обосновать, что:

Углы B и D, как вписанные будут равны: первый — половиной дуги ADС, второй — половиной дуги ABС. Следовательно, B + D равняется полусумме дуг ADС и ABС, т.е. половиной окружности. Значит, B + D = 2d. Подобно этому убедимся, что A + С= 2d .

Необходимо обосновать, что около такого четырехугольника можно описать окружность. Через какие-нибудь три его вершины, например, A, B, С прочертим окружность (что всегда можно сделать).

Четвертая вершина D должна располагаться на этой окружности, потому что в противном случае угол D лежал бы своей вершиной или внутри круга, или вне его, и тогда этот угол не измерялся бы половиной дуги ABС, поэтому сумма B + D не измерялась бы полусуммой дуг ADС и ABС, т.е. сумма B + D не равнялась бы 2d, что противоречит условию.

Следствия.

1. Из всех параллелограммов только около прямоугольника можно описать окружность.

2. Около трапеции можно описать окружность только тогда, когда она равнобедренная.

Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Многоугольник вписан в окружность если все его

Видео:№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Многоугольник. Свойства четырехугольников вписанных в окружность.

Если все вершины какого-нибудь многоугольника (ABCDE) лежат на окружности, то говорят, что этот многоугольник вписан в окружность, или что окружность описана около него.

Теорема.

В выпуклом вписанном четырехугольнике сумма противоположных углов равна двум прямым углам (2d).

Обратная теорема:

Если в выпуклом четырехугольнике сумма противоположных углов равна двум прямым углам (2d), то около него можно описать окружность.

Пусть ABCD — вписанный выпуклый четырехугольник. Необходимо обосновать, что:

Углы B и D, как вписанные будут равны: первый — половиной дуги ADС, второй — половиной дуги ABС. Следовательно, B + D равняется полусумме дуг ADС и ABС, т.е. половиной окружности. Значит, B + D = 2d. Подобно этому убедимся, что A + С= 2d .

Необходимо обосновать, что около такого четырехугольника можно описать окружность. Через какие-нибудь три его вершины, например, A, B, С прочертим окружность (что всегда можно сделать).

Четвертая вершина D должна располагаться на этой окружности, потому что в противном случае угол D лежал бы своей вершиной или внутри круга, или вне его, и тогда этот угол не измерялся бы половиной дуги ABС, поэтому сумма B + D не измерялась бы полусуммой дуг ADС и ABС, т.е. сумма B + D не равнялась бы 2d, что противоречит условию.

Следствия.

1. Из всех параллелограммов только около прямоугольника можно описать окружность.

2. Около трапеции можно описать окружность только тогда, когда она равнобедренная.

Видео:110. Окружность, описанная около правильного многоугольникаСкачать

Вписанные и описанные многоугольники

Вписанным в круг многоугольником называется такой многоугольник, вершины которого лежат на окружности. Описанным около круга многоугольником называется такой многоугольник, стороны которого касаются окружности.

Описанной около многоугольника окружностью называется окружность, проходящая через его вершины. Вписанной в многоугольник окружностью называется окружность, касающаяся его сторон.

Вписанный многоугольник

Описанный многоугольник

Если многоугольник взят произвольно, то в него нельзя вписать и около него нельзя описать окружность. Только многоугольники соответствующие некоторым правилам можно описать окружностью или вписать в них окружность.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Правила для многоугольников которые можно вписать в окружность и описать окружность вокруг них

Для треугольника всегда возможны и вписанная окружность и описанная окружность.

Для четырехугольника окружность можно вписать только в том случае, если суммы его противоположных сторон одинаковы. Из всех параллелограммов только в ромб и квадрат можно вписать окружность. Ее центр лежит на пересечении диагоналей.

Вокруг четырехугольника окружность можно описать только если сумма противоположных углов равна 180°. Из всех параллелограммов только около прямоугольника и квадрата можно описать окружность. Ее центр лежит на пересечении диагоналей.

Вокруг трапеции возможно описать окружность или в трапецию можно вписать окружность если трапеция равнобокая.

Видео:ЕГЭ. Описывающая многоугольник окружность.Скачать

Описанная и вписанная окружность

теория по математике 📈 планиметрия

Видео:9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

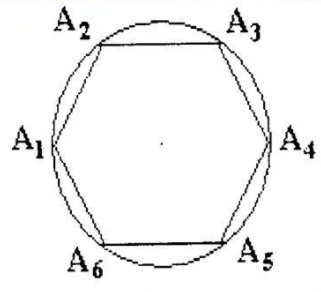
Описанная окружность

Окружность называется описанной вокруг многоугольника, если все вершины многоугольника принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.

Любой правильный многоугольник можно вписать в окружность. На рисунке описанная окружность проходит через каждую вершину правильного шестиугольника.

Видео:Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

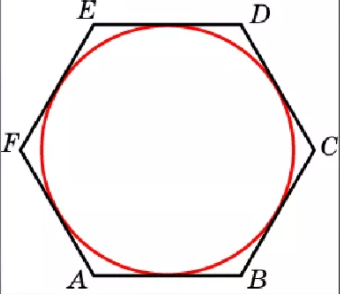
Вписанная окружность

Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в этом случае называется описанным около окружности.

В любой правильный многоугольник можно вписать окружность. На рисунке окружность вписана в правильный шестиугольник, она касается всех его сторон.

Вписанный и описанный треугольники

Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.

В любой треугольник можно вписать окружность: 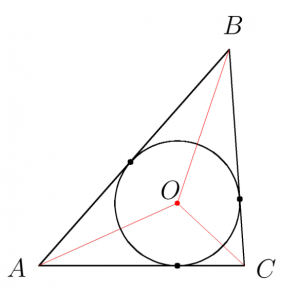Центр вписанной окружности

Центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.

Вписанный и описанный четырехугольники

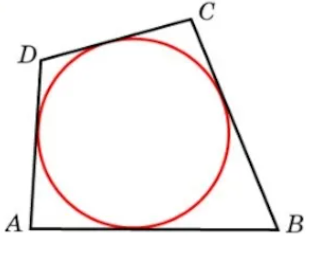
Не во всякий четырехугольник можно вписать окружность. Например, в прямоугольник нельзя вписать окружность. По рисунку видно, что окружность касается только трех его сторон, что не соответствует определению.

Условие вписанной в 4-х угольник окружности

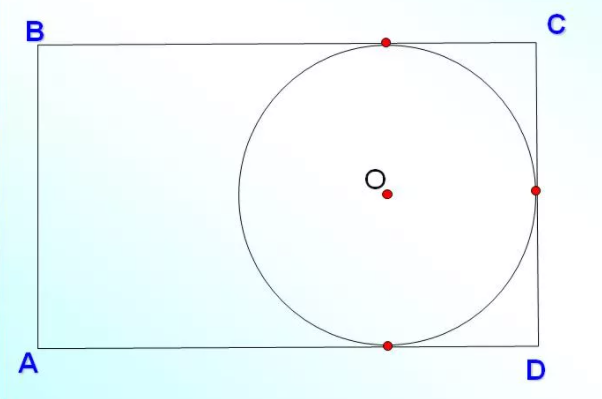
Окружность является вписанной в четырехугольник, если суммы длин противоположных сторон равны.

На рисунке выполняется данное условие, то есть AD + BC=DC + AB

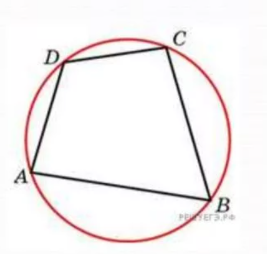
Окружность является описанной около четырехугольника, если суммы противоположных углов равны 180 градусов.

На рисунке окружности описана около четырехугольника, следовательно выполнено условие, что сумма углов А и С равна сумме углов B и D и равна 180 градусов.

📹 Видео

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

11 класс, 43 урок, Вписанный четырехугольникСкачать

78. Описанная окружностьСкачать

ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

8 класс. Многоугольник и его элементы. Многоугольник, вписанный в окружность и описанный около нейСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Правильный многоугольник в геометрии: примеры решения задачСкачать