Как появилась тригонометрическая окружность

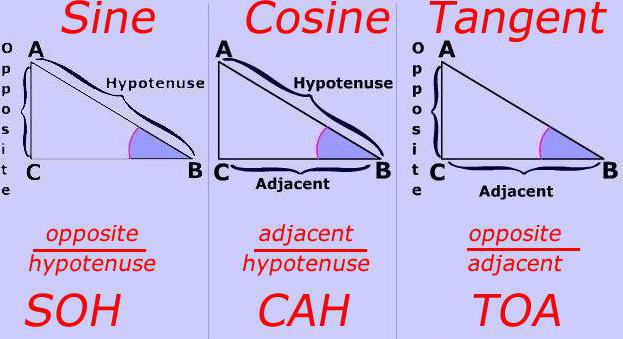
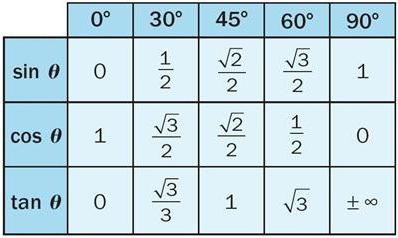
История тригонометрии неразрывно связана с астрономией, ведь именно для решения задач этой науки древние ученые стали исследовать соотношения различных величин в треугольнике.

На сегодняшний день тригонометрия является микроразделом математики, изучающим зависимость между значениями величин углов и длин сторон треугольников, а также занимающимся анализом алгебраических тождеств тригонометрических функций.

Видео:Тригонометрическая окружность. Как выучить?Скачать

Термин «тригонометрия»

Сам термин, давший название этому разделу математики, впервые был обнаружен в заголовке книги под авторством немецкого ученого-математика Питискуса в 1505 году. Слово «тригонометрия» имеет греческое происхождение и означает «измеряю треугольник». Если быть точнее, то речь идет не о буквальном измерении этой фигуры, а об её решении, то есть определении значений её неизвестных элементов с помощью известных.

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Общие сведения о тригонометрии

История тригонометрии началась более двух тысячелетий назад. Первоначально ее возникновение было связано с необходимостью выяснения соотношений углов и сторон треугольника. В процессе исследований выяснилось, что математическое выражение данных соотношений требует введения особых тригонометрических функций, которые первоначально оформлялись как числовые таблицы.

Для многих смежных с математикой наук толчком к развитию стала именно история тригонометрии. Происхождение единиц измерения углов (градусов), связанное с исследованиями ученых Древнего Вавилона, опирается на шестидесятиричную систему исчисления, которая дала начала современной десятиричной, применяемой во многих прикладных науках.

Предполагается, что изначально тригонометрия существовала как часть астрономии. Затем она стала использоваться в архитектуре. А со временем возникла целесообразность применения данной науки в различных областях человеческой деятельности. Это, в частности, астрономия, морская и воздушная навигация, акустика, оптика, электроника, архитектура и прочие.

Видео:ТРИГОНОМЕТРИЧЕСКАЯ ОКРУЖНОСТЬ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэ #окружностьСкачать

Тригонометрия в ранние века

Руководствуясь данными о сохранившихся научных реликвиях, исследователи сделали вывод, что история возникновения тригонометрии связана с работами греческого астронома Гиппарха, который впервые задумался над поиском способов решения треугольников (сферических). Его труды относятся ко 2 веку до нашей эры.

История развития тригонометрии в Древней Греции связана с именем астронома Птоломея — автора геоцентрической системы мира, господствовавшей до Коперника.

Греческим астрономам не были известны синусы, косинусы и тангенсы. Они пользовались таблицами, позволяющими найти значение хорды окружности с помощью стягиваемой дуги. Единицами для измерения хорды были градусы, минуты и секунды. Один градус приравнивался к шестидесятой части радиуса.

Также исследования древних греков продвинули развитие сферической тригонометрии. В частности, Евклид в своих «Началах» приводит теорему о закономерностях соотношений объемов шаров различного диаметра. Его труды в этой области стали своеобразным толчком в развитии еще и смежных областей знаний. Это, в частности, технология астрономических приборов, теория картографических проекций, система небесных координат и т. д.

Видео:Как искать точки на тригонометрической окружности.Скачать

Средневековье: исследования индийских ученых

Значительных успехов достигли индийские средневековые астрономы. Гибель античной науки в IV веке обусловила перемещение центра развития математики в Индию.

История возникновения тригонометрии как обособленного раздела математического учения началась в Средневековье. Именно тогда ученые заменили хорды синусами. Это открытие позволило ввести функции, касающиеся исследования сторон и углов прямоугольного треугольника. То есть именно тогда тригонометрия начала обосабливаться от астрономии, превращаясь в раздел математики.

Первые таблицы синусов были у Ариабхаты, они была проведены через 3 о , 4 о , 5 о . Позже появились подробные варианты таблиц: в частности, Бхаскара привел таблицу синусов через 1 о .

Видео:ТРИГОНОМЕТРИЧЕСКАЯ ОКРУЖНОСТЬСкачать

История развития тригонометрии в Европе

После перевода арабских трактатов на латынь (XII-XIII в) большинство идей индийских и персидских ученых были заимствованы европейской наукой. Первые упоминания о тригонометрии в Европе относятся к XII веку.

По мнению исследователей, история тригонометрии в Европе связана с именем англичанина Ричарда Уоллингфордского, который стал автором сочинения «Четыре трактата о прямых и обращенных хордах». Именно его труд стал первой работой, которая целиком посвящена тригонометрии. К XV веку многие авторы в своих трудах упоминают о тригонометрических функциях.

Видео:Тригонометрическая окружность для непонимающихСкачать

История тригонометрии: Новое время

В Новое время большинство ученых стало осознавать чрезвычайную важность тригонометрии не только в астрономии и астрологии, но и в других областях жизни. Это, в первую очередь, артиллерия, оптика и навигация в дальних морских походах. Поэтому во второй половине XVI века эта тема заинтересовала многих выдающихся людей того времени, в том числе Николая Коперника, Иоганна Кеплера, Франсуа Виета. Коперник отвел тригонометрии несколько глав своего трактата «О вращении небесных сфер» (1543). Чуть позже, в 60-х годах XVI века, Ретик — ученик Коперника — приводит в своем труде «Оптическая часть астрономии» пятнадцатизначные тригонометрические таблицы.

Видео:Тригонометрическая окружностьСкачать

Заслуги Леонарда Эйлера

Придание тригонометрии современного содержания и вида стало заслугой Леонарда Эйлера. Его трактат «Введение в анализ бесконечных» (1748) содержит определение термина «тригонометрические функции», которое эквивалентно современному. Таким образом, этот ученый смог определить обратные функции. Но и это еще не все.

Определение тригонометрических функций на всей числовой прямой стало возможным благодаря исследованиям Эйлера не только допустимых отрицательных углов, но и углов боле 360°. Именно он в своих работах впервые доказал, что косинус и тангенс прямого угла отрицательные. Разложение целых степеней косинуса и синуса тоже стало заслугой этого ученого. Общая теория тригонометрических рядов и изучение сходимости полученных рядов не были объектами исследований Эйлера. Однако, работая над решением смежных задач, он сделал много открытий в этой области. Именно благодаря его работам продолжилась история тригонометрии. Кратко в своих трудах он касался и вопросов сферической тригонометрии.

Видео:🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Области применения тригонометрии

Тригонометрия не относится к прикладным наукам, в реальной повседневной жизни ее задачи редко применяются. Однако этот факт не снижает ее значимости. Очень важна, например, техника триангуляции, которая позволяет астрономам достаточно точно измерить расстояние до недалеких звезд и осуществлять контроль за системами навигации спутников.

Также тригонометрию применяют в навигации, теории музыки, акустике, оптике, анализе финансовых рынков, электронике, теории вероятностей, статистике, биологии, медицине (например, в расшифровке ультразвуковых исследований УЗИ и компьютерной томографии), фармацевтике, химии, теории чисел, сейсмологиии, метеорологии, океанологии, картографии, многих разделах физики, топографии и геодезии, архитектуре, фонетике, экономике, электронной технике, машиностроении, компьютерной графике, кристаллографиии и т. д. История тригонометрии и ее роль в изучении естественно-математических наук изучаются и по сей день. Возможно, в будущем областей ее применения станет еще больше.

Видео:Как запомнить тригонометрический круг специально ничего не выучивая?Скачать

История происхождения основных понятий

История возникновения и развития тригонометрии насчитывает не один век. Введение понятий, которые составляют основу этого раздела математической науки, также не было одномоментным.

Слово «косинус» появилось намного позже. Этот термин является сокращенным вариантом латинской фразы «дополнительный синус».

Возникновение тангенсов связано с расшифровкой задачи определения длины тени. Термин «тангенс» ввел в X веке арабский математик Абу-ль-Вафа, составивший первые таблицы для определения тангенсов и котангенсов. Но европейские ученые не знали об этих достижениях. Немецкий математик и астроном Регимонтан заново открывает эти понятия в 1467 г. Доказательство теоремы тангенсов – его заслуга. А переводится этот термин как «касающийся».

Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Научно-практическая конференция «История развития тригонометрии»

1 ОБРАЗОВАТЕЛЬНЫЕ

1. Формирование умений и навыков применения полученных знаний на практике;
2. Использование новых образовательных технологий при решении поставленной задачи.

2 РАЗВИВАЮЩИЕ

1. Развитие углубленного интереса к изучаемому предмету;
2. Показать взаимосвязь математики и других наук и предметов;
3. Развитие познавательной и творческой деятельности студентов.

Воспитание заинтересованности историей математики и изучаемых в ней вопросов;

ТЕХНИЧЕСКИЕ СРЕДСТВА

1. Экран
2. Компьютер
3. Проектор

ХОД ВНЕКЛАССНОГО МЕРОПРИЯТИЯ

1 ОРГАНИЗАЦИОННЫЙ МОМЕНТ

1. Актуализация темы
2. Постановка цели и задач мероприятия

2 ПРЕДСТАВЛЕНИЕ

1. Выступление учителя
2. Выступление студентов с докладами

3 ЗАКЛЮЧЕНИЕ

1. Подведение итогов
2. Угадывание кроссворда
3. Рефлексия

Здравствуйте ребята. Мы собрались здесь в этом зале, чтобы перевернуть еще одну новую страницу в познании математики. Не так давно вы на уроках прошли один из самых интереснейших разделов. Это раздел » Тригонометрия » Сегодня мы с вами узнаем то, что вам поможет более лучше узнать этот предмет и применять его в других сферах жизни и на практике Добро пожаловать в страну Тригонометрию с ее замечательной историей, ее развитием, и великими людьми, теми, кто создал, развивал и двигал вперед науку (читается текст из черного листа).

Самой первой тригонометрической функцией была хорда соответствующая данной дуге. Для этой функции были построены первые тригонометрические таблицы нужные астрономии Первые тригонометрические таблицы (так называемые таблицы хорд) были составлены в древней Греции и были хорошо известны еще с 3 века до нашей эры.

Слово “тригонометрия” впервые встречается в 1505 году в заглавии книги немецкого теолога и математика Питискуса. Происхождение этого слова греческое rpiycovov — треугольник, fiETpeco — мера. Иными словами, тригонометрия наука об измерении треугольников. Тригонометрия выросла из человеческой практики, в процессе решения конкретных практических задач в областях астрономии, мореплавания и в составлении географических карт.

Наивысшими достижениями греческая тригонометрия обязана астроному Птолемею (II век н.э.), создателю геоцентрической системы мира, господствовавшей до Коперника.

Греческие астрономы не знали синусов, косинусов и тангенсов. Вместо таблиц этих величин они употребляли таблицы: позволяющие отыскать хорду окружности по стягиваемой дуге. Дуги измерялись в градусах и минутах; хорды тоже измерялись градусами (один градус составлял шестидесятую часть Радиуса), минутами и секундами. Это шестидесятеричное подразделение греки заимствовали у вавилонян.

В первом тысячелетии нашей эры происходит бурный расцвет культуры и науки в странах Арабского Халифата, и поэтому основные открытия тригонометрии принадлежат ученым этих стран. Туркменский ученый аль-Маразви первым ввел понятие tg и ctg как отношение сторон прямоугольного треугольника и составил таблицы sin, tg, и ctg. Основным достижением арабских ученых является то, что они отделили тригонометрию от астрономии.

Фактически различные отношения отрезков треугольника и окружности (а по существу тригонометрические функции) встречаются уже в III в. до н.э. В работах великих математиков Древней Греции Евклида, Архимеда, Апполония Пергского.

В римский период эти отношения уже достаточно систематично исследовались Монолаем (I в. н.э.), хотя и не приобрели специального названия. Современный синус угла а, например, изучался как полухорда, на которую опирается центральный угол величиной а, или как хорда удвоенной дуги.

Развиваясь в тесной связи с астрономией и географией,- среднеазиатская математика имела ярко выраженный «вычислительный характер» и была направлена на разрешение прикладных задач измерительной геометрии и тригонометрии. Из числа сделанных ими важнейших успехов следует в первую очередь отметить введение всех шести тригонометрических линий: синуса, косинуса, тангенса, котангенса, секанса и косеканса, из которых лишь первые две были известны грекам и индийцам.

В трудах среднеазиатских ученых тригонометрия превратилась из науки, обслуживающей астрономию, в особую математическую дисциплину, представляющую самостоятельный интерес.

Это отделение обычно связывают с именем азербайджанского математика Насирэддина Туси (1201-1274).

В «Трактате о полном четырехстороннике» впервые изложил тригонометрические сведения как самостоятельный отдел математики, а не придаток в астрономии.

Значительные высоты достигла тригонометрия и у индийских средневековых астрономов. Главным достижением индийских астрономов стала замена хорд синусами, что позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника.

Таким образом, в Индии было положено начало тригонометрии как учению о тригонометрических величинах. Индийские ученые пользовались различными тригонометрическими соотношениями, в том числе и теми, которые в современной форме выражается как:

sin а + cos а = 1,

sin а = cos (90 — а)

sin (а + b) = sin a. cos В + cos a. sin b

В IV-V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты. Отрезок СВ он назвал ардхаджива (ардха -половина, джива — тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus -изгиб, кривизна). Известный Мухаммед ибн Муса ал-Хорезми (IX в.) составил таблицы синусов и котангенсов. Ал-Хабаш вычислил таблицы для тангенса, котангенса и косеканса.

В первой половине XV века вычислил с большой точностью тригонометрические таблицы с шагом в 1°, которые на протяжении 250 лет оставались непревзойденными.

Наряду с синусом индийцы ввели в тригонометрию косинус, точнее говоря, стали употреблять в своих вычислениях линию косинуса. Им были известны также соотношения cosa=sin(90°-a) и sin2a+cos2a=r2, а также формулы для синуса суммы и разности двух углов.

Сам термин косинус появился значительно позднее в работах европейских ученых впервые в конце XVI в. из так называемого “синуса дополнения”, т.е. синуса угла, дополняющего данный угол до 90°. “Синус дополнения” или (по латыни) sinus complement! стали сокращенно записывать как sinus со или co-sinus.

Тангенсы возникли в связи с решением задач об определении длины тени. Тангенс (а также котангенс, секанс и косеканс) введен в X в. Арабским математиком Абу-л-Вафой, который составил первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными, европейским ученым, и тангенсы были заново открыты в XIV в.

Сначала английским ученым . Бравердином, позднее немецким математиком, астрономом Региомонтаном в 1467 г. Название “тангенс”, происходящее от tanger (касаться), появилось в 1583 г. Tangens переводится как —касающийся”.

Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке Аль — Батани (850-929) и Абу-ль-Вефа Мухамед-бен Мухаммед (940-998), который составил таблицы синусов и тангенсов через 10′ с точностью до 1/604.

Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XIV веке немецким математиком, астрономом Региомонтаном (1467 г.). Именно он доказал теорему тангенсов (латинизированное имя немецкого астронома и математика Иоганна Мюллера (1436-1476). Региомонтан составил также подробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе. Региомонтан — самый видный европейский представитель этой эпохи в области тригонометрии. Его обширные таблицы синусов через 1′ с точностью до 7-й значащей цифры и его мастерски изложенный тригонометрический труд “пять книг о треугольниках всех видов” имели большое значение для дальнейшего развития тригонометрии в XVI — XVII веках.

Его обширные таблицы синусов через 1* с точностью до 7-ой цифры и его изложенный тригонометрический труд “Пять книг о треугольниках всех видов” имели большое значение для дальнейшего развития тригонометрии в XVI — XVII вв.

Но общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка “арк” происходит от латинского areas (дуга), что вполне согласуется со смыслом понятия: arc sin х, например,- это угол (а можно сказать, и дуга), синус которого равен х.

Современные обозначения a res in и arctg появляются в 1772 году в работах венского математика Шерфера и известного французского учёного Ж.Л.Лагранжа. Хотя несколько ранее их уже рассматривал Д.Бернулли, который употреблял иную символику.

В XVII — XIX вв. тригонометрия становится одной из глав математического анализа. Она находит большое применение в механике, физике и технике, особенно при изучении колебательных движений и других периодических процессов.

Применял символы тригонометрических функций. Из физики известно, что уравнение гармонического колебания (например, колебания маятника) имеет вид:

у = Asin( wt+a) График гармонических колебаний называется синусоидой, поэтому в физике и технике сами гармонические колебания часто называют синусоидальными колебаниями.

Тригонометрия:

1. плоская — изучает только плоские треугольники
2. сферическая — изучает только сферические треугольники
3. прямолинейная — не входит в школьную программу.

Плоская тригонометрия начала развиваться позже сферической, хотя отдельные теоремы ее встречались и раньше, так например 12-я и 13-я теоремы второй книги “Начал” Евклида (III в. до н. э.) выражают по существу теорему косинусов. Плоская тригонометрия получила развитие у аль-Баттани (2-я половина IX — начало Хв.), Абу-ль-Вефа, Бхскала и Насиреддина Туси, которым была уже известна теорема синусов.

Тригонометрия, занимающаяся сферическими треугольниками, называется сферической, также она рассматривает соотношения между сторонами и углами треугольников на сфере, образованных дугами больших кругов. В работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным.

В наше время тригонометрия больше не рассматривается как самостоятельная ветвь математики. Важнейшая ее часть — учение о тригонометрических функциях — является частью более общего, построенного с единой точки зрения учения о функциях, изучаемых в математическом анализе; другая же часть- решение треугольников -рассматривается как глава геометрии.

Редко используемые тригонометрические функции — функции угла, которые в настоящее время используются редко по сравнению с шестью основными тригонометрическими функциями (синусом, косинусом, тангенсом, котангенсом,

секансом и косекансом). К ним относятся:

Кривошипно-шатунный механизм служит для преобразования равномерного вращательного движения конца кривошипа в неравномерное прямолинейное движение ползуна, и обратно. Аналогично работает двигатель автомобиля.

Электромагнитные колебания доносят до нас вести о сложнейших процессах, происходящих внутри звезд, о взрывах в отдаленных галактиках. С помощью электромагнитных колебаний советскими учеными были получены снимки обратной стороны Луны. Такие колебания сопровождают и биологические процессы, например передачу возбуждения по нервной ткани, работу сердца и мозга. Записывая их, врачи получают электрокардиограммы и энцефалограммы

Уравнение гармонического колебания имеет вид: у = A sin ( )

График гармонических колебаний называется синусоидой, поэтому в физике и технике сами гармонические колебания часто называют синусоидальными колебаниями.

Одним из простейших видов колебаний является движение по оси проекции точки М, которая равномерно вращается по окружности. х= R cos( t+ ).

При решении многих задач удобнее пользоваться так называемыми полярными координатами: на плоскости выбирают неподвижную точку О (полюс) и выходящий из нее луч ОР (полярная ось). Положение точки М в этом случае определяется двумя числами: ее расстоянием г от полюса и углом у — угол РОМ. Числа г (полярный радиус) и ф (полярный угол) называются полярными координатами точки М.

Часто оказывается полезным рассматривать на плоскости полярную систему координат вместе с декартовой. Рассмотрим такое расположение, когда полюсом служит начало декартовой системы, а полярной осью — ось абсцисс; рисунок сам подсказывает связь между полярными и декартовыми координатами точки:

Уравнения, найденные немецким математиком-натуралистом Хабенихтом для геометрических форм, встречающихся в мире растений.

Например, уравнениям r=4(l+cos3(p) и r=4(l+cos3(p)+4sin23(p

Рассмотрим кривые sin

При а=0 (рис.1 ), при а= 1/2 (рис.2), при а=1 (рис.3) лепестки имеют законченный вид, при а=3/2 будет пять незаконченных лепестков., (рис.4).

Кривые Лиссажу, характеризуемые в общем случае уравнениями:

В общем случае кривая располагается внутри прямоугольника со сторонами 2а и2в. Кривые могут быть замкнутыми и незамкнутыми. Рассмотрим это на следующих примерах:

В данной презентации максимально сжато рассказано о тригонометрии. Если вы хотите знать её в совершенстве, то это потребует не один год.

Вы сегодня узнали много нового из жизни тригонометрических функций А теперь я предлагаю вам немного расслабиться и поиграть. Хотите Ну что ж попытайтесь угадать какая тригонометрическая функция обращается:

Я и сама могу сказать
И график свой вам показать
Хоть есть названье у линии моей
И нет как у параболы ветвей
Я отрицательна-и это всем вам видно
Не жмусь волной одним концом к оси ОХ я безобидно
Давно сравнили мою скорость роста
Ты по сравнению со мной малютка просто ( у= sin х)
Скучна я — так часто говорят
И монотонной называют
Что график мой не держит взгляд
Симметрию в нем отмечают
Не возрастаю, а спускаюсь вниз
И веток много я имею
И вам открою я секрет
Отображаться я умею ( ко тангенс )

Друзья поверьте мне
Я самая полезная
Интересная и лирическая
Я функция — тригонометрическая
Имею я особенную точку.
О ней скажу вам я в последней строчке
То точки ноль и единица
И хоть мой график тут наверх стремиться
В любом он случае через нее проходит
И два конца волны в единый график сводит (косинус)

Видео:СУТЬ ТРИГОНОМЕТРИИСкачать

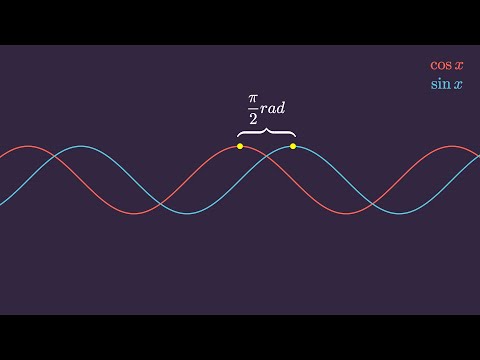
Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников (trigwnon — треугольник, а metrew- измеряю).

В данном случае измерение треугольников следует понимать как решение треугольников, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, а также задач планиметрии, стереометрии, астрономии и других приводятся к задаче решения треугольников.

Возникновение тригонометрии связано с землемерием, астрономией и строительным делом.

Хотя название науки возникло сравнительно недавно, многие относимые сейчас к тригонометрии понятия и факты были известны ещё две тысячи лет назад.

Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями.

Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929) и Абу-ль-Вафа, Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через 10’ с точностью до 1/604. Теорему синусов уже знали индийский ученый Бхаскара (р. 1114, год смерти неизвестен) и азербайджанский астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе «Трактат о полном четырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.

Длительную историю имеет понятие синус. Фактически различные отношения отрезков треугольника и окружности (а по существу, и тригонометрические функции) встречаются уже в III веке до н.э. в работах великих математиков Древней Греции – Евклида, Архимеда, Апполония Пергского. В римский период эти отношения достаточно систематично исследовались Менелаем (I век н.э.), хотя и не приобрели специального названия. Современный синус a, например, изучался как полухорда, на которую опирается центральный угол величиной a, или как хорда удвоенной дуги.

В IV-V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли. Отрезок АМ (рис. 1) он назвал ардхаджива (ардха – половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus – изгиб, кривизна).

Слово косинус намного моложе. Косинус – это сокращение латинского выражения completely sinus, т. е. “дополнительный синус” (или иначе “синус дополнительной дуги”; cosa = sin( 90° — a)).

Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XIV веке немецким математиком, астрономом Регимонтаном (1467 г.). Он доказал теорему тангенсов. Региомонтан составил также подробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе.

Название «тангенс», происходящее от латинского tanger (касаться), появилось в 1583 г. Tangens переводится как «касающийся» (линия тангенсов – касательная к единичной окружности).

Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) – творца гелиоцентрической системы мира, Тихо Браге (1546-1601) и Иогана Кеплера (1571-1630), а также в работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным.

Долгое время тригонометрия носила чисто геометрический характер, т. е. Факты, которые мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Пожалуй, наибольшие стимулы к развитию тригонометрии возникали в связи с решением задач астрономии, что представляло большой практический интерес (например, для решения задач определения местонахождения судна, предсказания затемнения и т. д.). Астрономов интересовали соотношения между сторонами и углами сферических треугольников. И надо заметить, что математики древности удачно справлялись с поставленными задачами.

Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики.

Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук. Громадное научное наследие Эйлера включает блестящие результаты, относящиеся к математическому анализу, геометрии, теории чисел, механике и другим приложениям математики. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее проще,

Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.

Позднее часть тригонометрии, которая изучает свойства тригонометрических функций и зависимости между ними, начали называть гониометрией (в переводе – наука об измерении углов, от греческого gwnia — угол, metrew- измеряю). Термин гониометрия в последнее время практически не употребляется.

А теперь посмотрите фильм о развитии математики, на 29 минуте — о тригонометрии.

📹 Видео

итак тригонометрия и тригонометрическая окружностьСкачать

10 класс, 11 урок, Числовая окружностьСкачать

Тригонометрические функции и их знакиСкачать

Тригонометрия с нуля. Часть 1. Единичная окружностьСкачать

✓ Тригонометрия: с нуля и до ЕГЭ | #ТрушинLive #030 | Борис ТрушинСкачать

Тригонометрическая окружностьСкачать

Тригонометрическая окружность в ЕГЭ. Как запомнить? | УмскулСкачать

Таблица значений тригонометрических функций - как её запомнить!!!Скачать

12 часов Тригонометрии с 0.Скачать