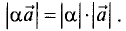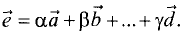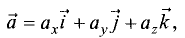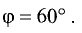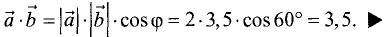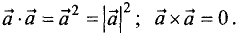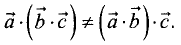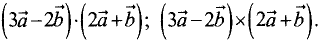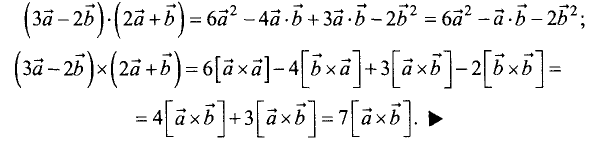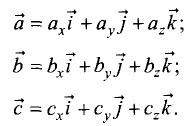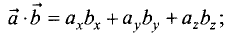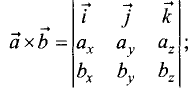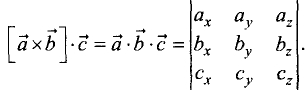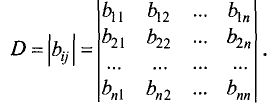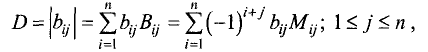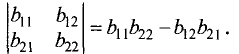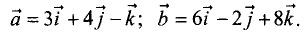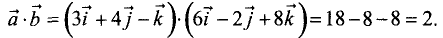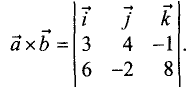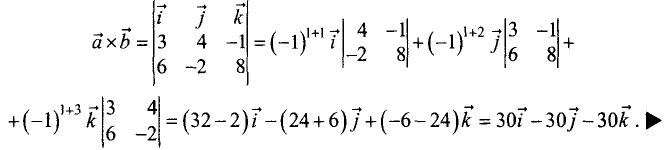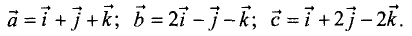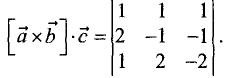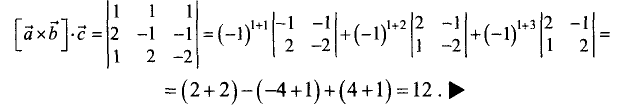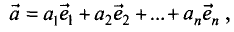Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .
Существование: Имеем два следующих случая:
Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .
Из данного выше построения сразу же будет следовать единственность данного вектора.
- Сумма векторов. Сложение векторов. Правило треугольника
- Разность векторов. Вычитание векторов
- Умножение вектора на число
- Сумма и разность векторов
- Сумма векторов
- Формула сложения векторов
- Свойства сложения векторов
- Разность векторов
- Формула вычитания векторов
- Примеры задач
- Операции над векторами с примерами решения и образцами выполнения
- Операции над векторами
- Умножение вектора на скаляр
- Сложение векторов
- Линейная комбинация векторов
- Координаты точки
- Умножение векторов
- Выражения произведений векторов в прямоугольной декартовой системе координат
- 🎬 Видео
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Сумма векторов. Сложение векторов. Правило треугольника
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.
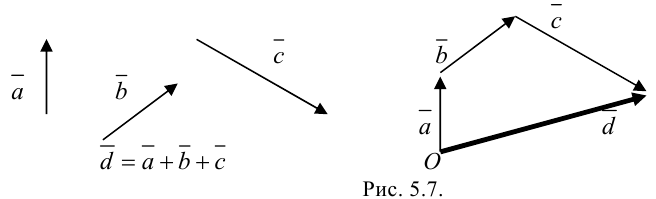
Суммой нескольких векторов ( vec ) , ( vec ) , ( vec,;ldots ) называется вектор ( vec ) , получающийся в результате последовательного сложения данных векторов.
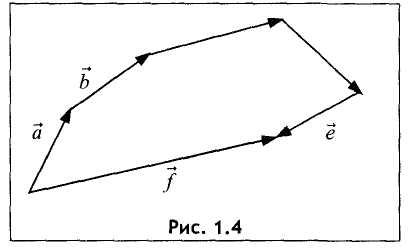
Такая операция выполняется по правилу многоугольника.
Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( <+ , + , + > right) )
Отметим несколько свойств сложения двух векторов:
Для произвольного вектора ( overrightarrow ) выполняется равенство
Для произвольных точек ( A, B и C ) справедливо следующее равенство
Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.
Видео:Сложение векторов. 9 класс.Скачать

Разность векторов. Вычитание векторов
Разность двух одинаковых векторов равна нулевому вектору :
( vec — vec = vec )
Длина нулевого вектора равна нулю:
( left| vec right| = 0 )
Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec — vec = left( <- , — , — > right) )
Видео:Вычитание векторов. 9 класс.Скачать

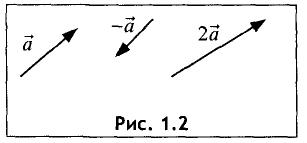
Умножение вектора на число
Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .
Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:
Длина вектора ( overrightarrow ) равна ( left|overrightarrowright|=left|kright||overrightarrow| ) ;
Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )
Обозначение: ( overrightarrow=koverrightarrow ) .
Видео:8 класс, 43 урок, Сумма двух векторовСкачать

Сумма и разность векторов
В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.
Видео:8 класс, 45 урок, Сумма нескольких векторовСкачать

Сумма векторов
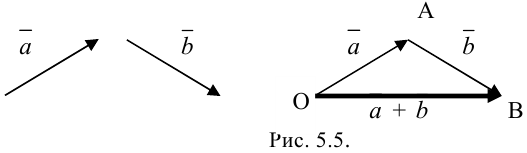
Сложение векторов выполняется по правилу треугольника.
Геометрическая интерпретация:
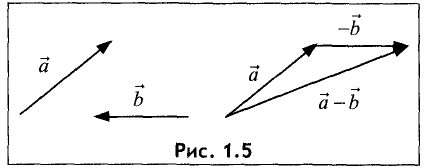
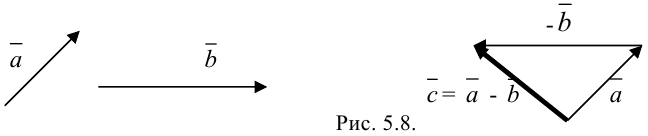
Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .
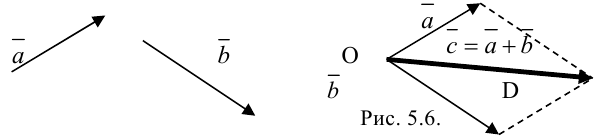
Для сложения векторов также используется правило параллелограмма.
Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.
Формула сложения векторов
Элементы вектора c равняются попарной сумме соответствующих элементов a и b .
<table data-id="250" data-view-id="250_55602" data-title="Формулы сложения векторов" data-currency-format="$1,000.00" data-percent-format="10.00%" data-date-format="DD.MM.YYYY" data-time-format="HH:mm" data-features="["after_table_loaded_script"]" data-search-value="" data-lightbox-img="" data-head-rows-count="1" data-pagination-length="50,100,All" data-auto-index="off" data-searching-settings="» data-lang=»default» data-override=»» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>
<td data-cell-id="B1" data-x="1" data-y="1" data-db-index="1" data-cell-type="text" data-original-value=" a + b = <ax + bx; ay + by> » data-order=» a + b = <ax + bx; ay + by> » style=»min-width:55.0847%; width:55.0847%;»> a + b = <ax + bx; ay + by>
<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value=" a + b = <ax + bx; ay + by; az + bz> » data-order=» a + b = <ax + bx; ay + by; az + bz> «> a + b = <ax + bx; ay + by; az + bz>
<td data-cell-id="B3" data-x="1" data-y="3" data-db-index="3" data-cell-type="text" data-original-value=" a + b = <a1 + b1; a2 + b2; . an + bn> » data-order=» a + b = <a1 + b1; a2 + b2; . an + bn> «> a + b = <a1 + b1; a2 + b2; . an + bn>
Свойства сложения векторов
1. Коммутативность: a + b = b + a
2. Ассоциативность: ( a + b ) + c = a + ( b + c )
3. Прибавление к нулю: a + 0 = a
4. Сумма противоположных векторов: a + (- a ) = 0
Примечание: Вектор – a коллинеарен и равен по длине a , но имеет противоположное направление, из-за чего называется противоположным.
Видео:Геометрия 9 класс (Урок№2 - Сумма двух векторов. Законы сложения векторов.)Скачать

Разность векторов
Для вычитания векторов также применяется правило треугольника.
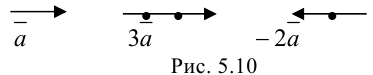
Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие:
Формула вычитания векторов
Элементы вектора c равны попарной разности соответствующих элементов a и b .
<table data-id="251" data-view-id="251_83403" data-title="Формулы вычитания векторов" data-currency-format="$1,000.00" data-percent-format="10.00%" data-date-format="DD.MM.YYYY" data-time-format="HH:mm" data-features="["after_table_loaded_script"]" data-search-value="" data-lightbox-img="" data-head-rows-count="1" data-pagination-length="50,100,All" data-auto-index="off" data-searching-settings="» data-lang=»default» data-override=»» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>
<td data-cell-id="B1" data-x="1" data-y="1" data-db-index="1" data-cell-type="text" data-original-value=" a — b = <ax — bx; ay — by> » data-order=» a — b = <ax — bx; ay — by> » style=»min-width:55.0847%; width:55.0847%;»> a — b = <ax — bx; ay — by>
<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value=" a — b = <ax — bx; ay — by; az — bz> » data-order=» a — b = <ax — bx; ay — by; az — bz> «> a — b = <ax — bx; ay — by; az — bz>
<td data-cell-id="B3" data-x="1" data-y="3" data-db-index="3" data-cell-type="text" data-original-value=" a — b = <a1 — b1; a2 — b2; . an — bn> » data-order=» a — b = <a1 — b1; a2 — b2; . an — bn> «> a — b = <a1 — b1; a2 — b2; . an — bn>
Видео:Построить разность векторов.Скачать

Примеры задач
Задание 1
Вычислим сумму векторов и .
Задание 2
Найдем разность векторов и .
Видео:СУММА ВЕКТОРОВ правило треугольникаСкачать

Операции над векторами с примерами решения и образцами выполнения
Под операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
1). Сложение векторов
Пусть 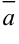
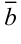
Сумму векторов можно найти по следующим правилам:
Выберем произвольную точку 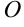
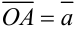
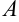
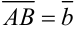
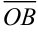
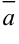
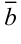
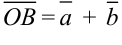
- Правило параллелограмма
Выберем произвольную точку 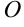
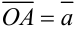
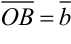
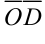
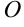
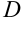
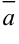
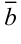
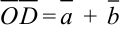
- Правило многоугольника:
Для нахождения суммы трех и более векторов используют правило многоугольника. Выберем произвольную точку 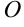
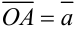
2). Вычитание векторов.
Под разностью векторов 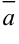
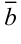
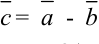
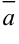
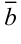
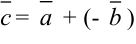
Отметим, что в параллелограмме, построенном на векторах 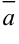
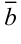
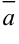
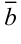
3). Умножение вектора на число.
Произведением вектора 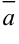
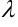
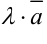
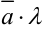
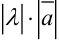
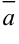
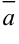
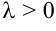
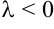
Например, если дан вектор 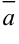
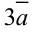
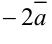
Линейные операции над векторами обладает следующими свойствами:
— свойство коммутативности,
— свойство ассоциативности,
.
Эти свойства позволяют проводить преобразования в линейных операциях с вектором так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать выносить за скобки как скалярные, так и векторные общие множители.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
Видео:Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Операции над векторами
Величины, значения которых могут быть выражены действительными числами, называются скалярами.
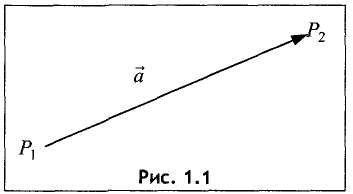
Вектором называется величина, определяемая числовым значением и направлением в пространстве (рис. 1.1).
Обозначается вектор различными способами: 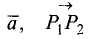
Длина вектора называется его модулем и обозначается
Единичным вектором называется вектор, длина которого
равна единице.
Нулевым вектором называется вектор, модуль которого равен
нулю, а направление не определено.
Два вектора называются равными, если равны их модули и
совпадают направления.
Свободные векторы получаются из данного вектора 
параллельного переноса.
Скользящие векторы получаются из данного вектора 
переноса вдоль прямой, на которой лежит вектор 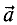
Связанные векторы — это векторы, которые нельзя переносить,
например, по физическим причинам.
Видео:сложение ВЕКТОРОВ вычитание ВЕКТОРОВ 9 класс геометрия АтанасянСкачать
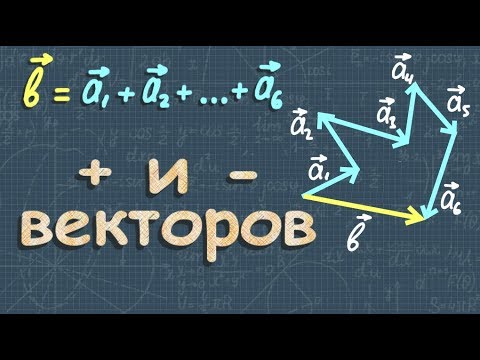
Умножение вектора на скаляр
Если 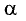
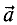
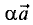
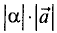
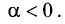
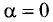
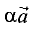
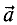
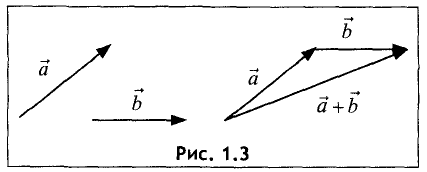
Сложение векторов
Сумма 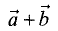
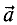
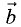
получающимся при параллельном переносе вектора 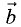
начало совпадает с концом вектора 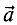
совпадает с началом вектора 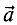
совпадает с концом вектора 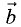
приведен пример сложения двух векторов.
Сумма нескольких векторов 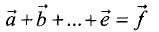
вектором 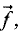
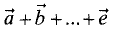
Разность векторов 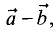
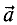
1. 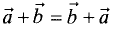
2. 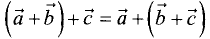
3. 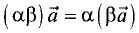
4. 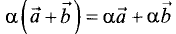
5. 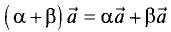
6.
Линейная комбинация векторов
Линейной комбинацией векторов 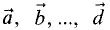
коэффициентами 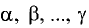
Коллинеарными называют два вектора 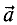
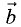
комбинация которых с некоторыми действительными числами 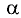
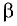
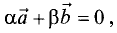
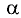
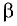
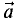
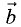
Компланарными называют три вектора 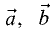
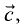
комбинация которых с некоторыми действительными числами 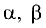
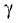
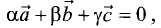
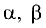
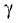
одновременно нулю. Геометрический смысл: векторы 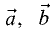
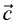
параллельны одной плоскости.
Линейно независимыми векторами на плоскости называются два
вектора, если они не коллинеарные, а в трехмерном пространстве —
три вектора, если они не компланарные.
Два или три ортогональных (перпендикулярных) вектора являются линейно независимыми и образуют двойку или тройку
линейно независимых векторов.
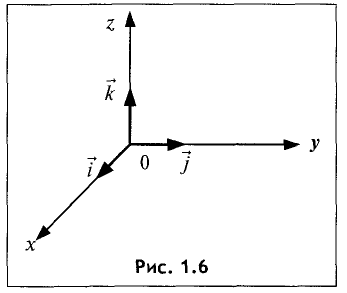
Если три единичных взаимно перпендикулярных вектора
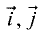
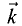
являются базой прямоугольной декартовой системы координат
(рис. 1.6).
Такие векторы называются ортами координат.
Система координат называется правой потому, что векторы
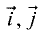
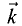
большой, указательный и средний пальцы правой руки. Для
определения правого направления системы координат может быть
использовано правило правого винта: если винт вкручивается в ось Oz со стороны нуля, то отвертка вращается от х к у.
Вектор 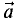
записывается в виде
где 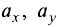
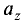
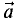
или проекции этого вектора на соответствующие оси.
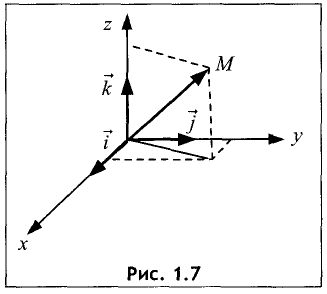
Координаты точки
Дана прямоугольная декартова система координат (рис. 1.7). В этой системе координат каждой точке М однозначно соответствует вектор 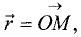
М. Декартовы координаты вектора 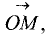
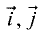
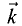
называются декартовыми координатами точки М.
Видео:Сложение нескольких векторов. Правило многоугольникаСкачать

Умножение векторов
Скалярное произведение векторов 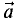
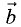
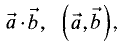
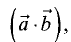
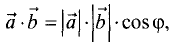
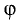
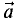
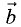
Пример:
Определить скалярное произведение векторов 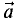
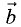
при 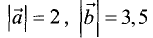
Решение:
Пример:
Определить скалярное произведение между каждой
из орт 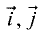
Решение:
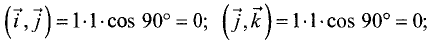
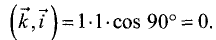
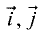
координат равно нулю. ►
Пример:
Определить скалярное произведение любой из орт
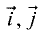
Решение:
Для примера рассмотрим орту 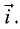
результат аналогичен. 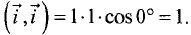
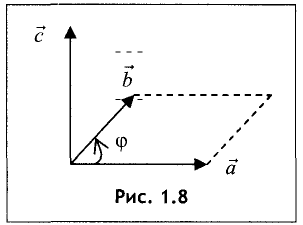
Векторное произведение векторов 
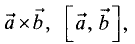
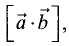
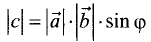
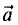
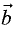
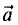
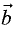
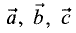
векторов (рис. 1.8).
Пример:
Определить векторное произведение между каждой
из орт 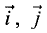
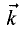
Решение:
Для примера рассмотрим векторное произведение
между векторами 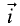
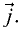
аналогичен, 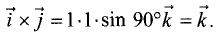
Произведения векторов обладают следующими свойствами:
1. 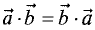
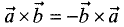
2. 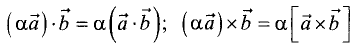
3. 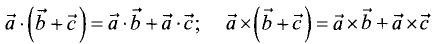
4. 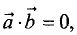
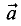
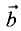
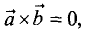
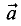
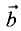
коллинеарные.
5.
6.В общем случае
Смешанное произведение 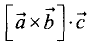
параллелепипеда, построенного на векторах 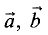
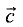
Пример:
Упростить выражения
Решение:
Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Выражения произведений векторов в прямоугольной декартовой системе координат
Пусть даны векторы:
Используя правила умножения векторов, можно показать
справедливость следующих формул:
■ для скалярного произведения
■ для векторного произведения
■ для смешанного произведения
Для векторного и смешанного произведений результаты
представлены в виде определителей.
Определителем (детерминантом) n-го порядка называется число D,
образованное из 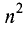
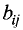
При вычислении определителя 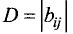
разложить на сумму произведений всех элементов какой-либо
строки (или столбца), умноженных на соответствующие им
алгебраические дополнения, по формуле
где 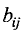
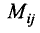
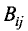
Таким образом, определитель 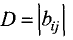
Определитель второго порядка вычисляется по формуле
Пример:
Найти скалярное и векторное произведения векторов:
Решение:
Скалярное произведение векторов
Векторное произведение векторов находим по формуле
Разложим данный определитель по первой строке и найдем
векторное произведение:
Пример:
Найти смешанное произведение векторов:
Решение:
Смешанное произведение находим по формуле
Разложим данный определитель по первой строке и найдем
векторное произведение:
В n-мерной системе координат вектор может быть представлен в виде
где 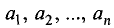
ось, вторую и т.д.;
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🎬 Видео
10 класс, 41 урок, Сумма нескольких векторовСкачать

Координаты вектора. 9 класс.Скачать

Сложение коллинеарных векторовСкачать

8 класс, 44 урок, Законы сложения векторов. Правило параллелограммаСкачать

Правило параллелепипеда для векторовСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Урок 8. Векторные величины. Действия над векторами.Скачать

83. Законы сложения векторов. Правило параллелограммаСкачать











 — свойство коммутативности,
— свойство коммутативности,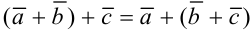 — свойство ассоциативности,
— свойство ассоциативности,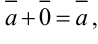
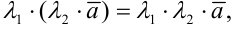
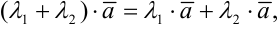
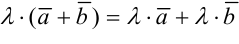 .
.