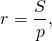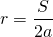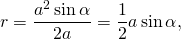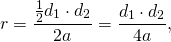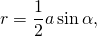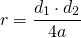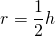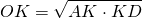Как построить ромб в окружности (2 видео)

Как нарисовать ромб самостоятельно: два способа

Иногда появляется необходимость сделать элементарное дело, при этом обнаруживается, что мы не знаем, как это сделать. Например — как нарисовать ромб. На самом деле все очень просто.

В данной статье вы узнаете, как правильно нарисовать ромб, и что это за геометрическая фигура.

Содержание

Что такое ромб?
Как нарисовать ромб
Вписанная в ромб окружность
§ 8. Аксонометрические проекции предметов, имеющих круглые поверхности
🎥 Видео

Видео:Как построить ромб по одному размеру. Дополнение к новогоднему видео.Скачать

Что такое ромб?

Ромб является разновидностью параллелограмма, особенностью которого является то, что противоположные стороны этой фигуры параллельны друг к другу, а у ромба они еще и равны между собой. Об определении ромба к общему виду параллелограмма говорит факт равенства противоположных углов.

Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Как нарисовать ромб

Нарисовать такую фигуру как ромб можно несколькими способами. В этой статье мы рассмотрим два простых способа.

Для первого способа нам понадобятся: ручка или карандаш, ластик, лист в клетку из школьной тетради, линейка или любой похожий на него прямой предмет, если размеры точные размеры ромба не важны.

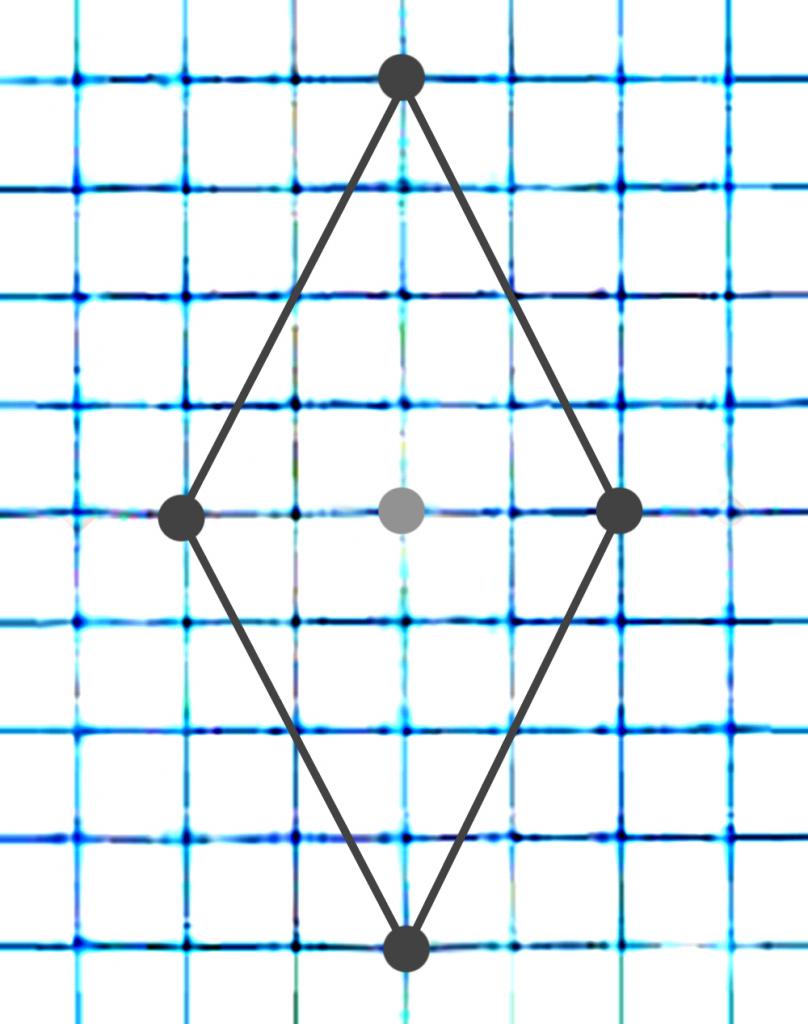
Итак, для начала нарисуем точку на одном из пересечений линий клеток. Лучше, конечно, разместить точку не слишком близко к краям. Определяемся с размерами фигуры.
Далее от средней точки отсчитываем необходимое количество клеток влево (или вправо) и ставим еще одну точку. В противоположной стороне через такое же количество клеток рисуем третью точку. Теперь то же самое проделываем по направлению вверх и вниз. Последовательность не имеет значения, главное здесь – отсчитать одинаковое расстояние от средней точки влево и вправо и отдельно вверх и вниз. То есть, если направо отсчитали четыре клетки, а вверх шесть клеток, соответственно, влево четыре клетки, вниз шесть клеток.

Соединяем линейкой или любым другим подходящим предметом все точки между собой, кроме среднего. Среднюю точку можно стереть ластиком, если вы использовали карандаш. Ромб готов.

Второй способ аналогичен первому, но рисовать мы будем на чистой бумаге без клеток. Нам нужно для этого: карандаш и/или ручка, ластик, чистый лист, линейка и угольник (или любой предмет с прямым углом).

Определяемся с размерами. Рисуем точку.
Берем линейку, ставим точку на необходимом расстоянии от средней точки на левой стороне. Соединяем их карандашом, чтобы линия проходила через среднюю точку. Аналогичные действия производим и в противоположную сторону.
Также рисуем точку сверху и снизу, но уже пользуемся угольником, чтобы линия между верхней и нижней точкой была перпендикулярна линии между левой и правой.
Соединяем все точки между собой. Стираем ластиком линии посередине фигуры.

Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

Вписанная в ромб окружность

Какими свойствами обладает вписанная в ромб окружность? Как найти её радиус?

Центр вписанной в ромб окружности — точка пересечения его диагоналей.

Радиус вписанной в ромб окружности можно найти по общей формуле

где S — площадь ромба, p — его полупериметр.

Так как полупериметр ромба равен p=2a, где a — сторона ромба, эту формулу можно записать как

С учётом формул для нахождения площади ромба:

где α — угол ромба (причем α может быть как острым, так и тупым).

где d1и d2 — диагонали ромба.

Таким образом, еще две формулы радиуса вписанной в ромб окружности:

Так как диаметр вписанной окружности равен высоте ромба, радиус равен половине высоты ромба:

Если известно, что точка касания вписанной окружности делит сторону ромба на отрезки, то радиус можно выразить через длины этих отрезков.

Так как диагонали ромба взаимно перпендикулярны и радиус, проведённый в точку касания, перпендикулярен стороне, то по свойству высоты прямоугольного треугольника из треугольника AOD имеем

Следовательно, радиус вписанной в ромб окружности есть среднее пропорциональное между отрезками, на которые делит сторону точка касания:

Видео:Построение пятиугольника циркулемСкачать

§ 8. Аксонометрические проекции предметов, имеющих круглые поверхности

8.1. Фронтальные диметрические проекции окружностей. Если на аксонометрическом изображении хотят некоторые элементы. например окружности (рис. 64), сохранить неискаженными, то применяют фронтальную диметрическую проекцию. Построение фронтальной диметрической проекции детали с цилиндрическим отверстием, два вида которой даны на рисунке 64, а, выполняют так:

Пользуясь осями х, у, z, строят тонкими линиями очертания внешней формы детали (рис. 64, б).
Находят центр отверстия на передней грани. Через него параллельно оси у проводят ось отверстия и откладывают на ней половину толщины детали. Получают центр отверстия, расположенный на задней грани.
Из полученных точек как из центров проводят окружности, диаметр которых равен диаметру отверстия (рис. 64, в).
Удаляют лишние линии и обводят видимый контур детали (рис. 64, г).

Рис. 64. Построение фронтальной диметрической проекции

Постройте в рабочей тетради фронтальную диметрическую проекцию детали, изображенной на рисунке 64, а. Ось у направьте в другую сторону. Величину изображения увеличьте примерно в два раза.

8.2. Изометрические проекции окружностей. Изометрической проекцией окружности (рис. 65) является кривая, которая называется эллипсом. Эллипсы строить трудно. В практике черчения вместо них часто строят овалы. Овал — замкнутая кривая, очерченная дугами окружностей. Овал удобно строить, вписывая в ромб, который является изометрической проекцией квадрата.

Рис. 65. Изображение в изометрической проекции окружностей вписанных в куб

Построение овала, вписанного в ромб, выполняют в такой последовательности.

Вначале строят ромб со стороной, равной диаметру изображаемой окружности (рис. 66, а). Для этого через точку О проводят изометрические оси х и у. На них от точки О откладывают отрезки, равные радиусу изображаемой окружности. Через точки а, b, с и d проводят прямые, параллельные осям; получают ромб.

Рис. 66. Построение овала

Большая ось овала располагается на большой диагонали ромба.

После этого вписывают в ромб овал. Для этого из вершин тупых углов (точек А и В) описывают дуги. Их радиус R равен расстоянию от вершины тупого угла (точек А и В) до точек с, d или a, b соответственно (рис. 66, б).

Через точки В и а, В и b проводят прямые. В пересечении прямых Ва и ВЬ с большей диагональю ромба находят точки С и D (рис. 66, а). Эти точки будут центрами малых дуг. Их радиус R1 равен Са (или Db). Дугами этого радиуса плавно соединяют большие дуги овала.

Мы рассмотрели построение овала, лежащего в плоскости, перпендикулярной оси z (овал 1 на рисунке 65). Овалы, находящиеся в плоскостях, перпендикулярных оси у (овал 2) и оси х (овал 3), строят также. Только для овала 2 построение ведут на осях х и z (рис. 67, а), а для овала 3— на осях у и z (рис. 67, б). Рассмотрим, как применяются изученные построения на практике.

Рис. 67. Построение овалов: а лежащего в плоскости, перпендикулярной оси у; б — лежащего в плоскости, перпендикулярной оси x

Рис. 68. Построение изометрической проекции детали с цилиндрическим отверстием

8.3. Способ построения аксонометрических проекций предметов, имеющих круглые поверхности. На рисунке 68, а дана изометрическая проекция планки. Надо изобразить цилиндрическое отверстие, просверленное перпендикулярно передней грани. Построение выполняют так:

Находят центр отверстия па передней грани. Определяют направление изометрических осей лля построения ромба (см. рис. 65). Из найденного центра проводят оси (рис. 68, а) и откладывают на них отрезки, равные радиусу окружности.
Строят ромб. Проводят его большую диагональ (рис. 68, б).
Описывают большие дуги. Находят центры для малых дуг (рис. 68. в).
Проводят из найденных центров малые дуги.

Такой же овал строят на задней грани, но обводят лишь видимую его часть (рис. 68, г).

Рис. 69. Задание для упражнений

Стороны ромбов на рисунке 65 равны 30 мм. Чему равны диаметры окружностей, проекции которых представлены овалами, вписанными в эти ромбы?

Постройте овалы, соответствующие проекциям окружностей, вписанных в грани куба, данного в изометрической проекции (по примеру на рисунке 65). Сторона куба равна 80 мм.